PER-KOM-BİN-OL - 7 01 ) Milli maç için A takımındaki 8 B
advertisement

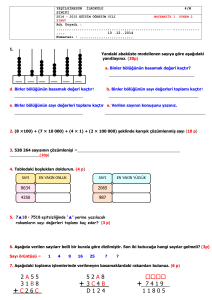
PER-KOM-BİN-OL - 7 01 ) Milli maç için A takımındaki 8 B takımındaki 5 futbolcu arasından2 futbolcu seçilecektir. Bu iki futbolcunun da A takımın 14 dan olma olasılığı nedir? c: 39 02 ) bir çift zar havaya atıldığı zaman üst yüzlerindeki sayılar toplamının 8 veya üst yüzdeki iki sayının çift olma olasılığı? c : 1136 03 ) Atılan iki zardan en az birisinin 4 geldiği biliniyor. Buna göre toplamlarının 7 den küçük olma olasılığı nedir? c : 114 04 ) 5 matematikçi 4 fizikçi ve 3 kimyacı arasından 4 kişilik bir bilim kurulu oluşturulacaktır. Bu kurulda en az 3 kişinin matema- c : 335 tikçi olma olasılığı nedir? 05 ) 1 den 30 a kadar olan doğal sayılar kartlara yazılarak bir torbaya atılıyor. Torbadan rasgele alınan 2 kartın üzerindeki sayılar 85 çarpımının asal sayı olmama olasılığı kaçtır? c: 87 06 ) 3x0y şeklinde yazılabilecek dört basamaklı sayıların içinden seçilen herhangi bir tanesinin 2 ile bölünebilen bir sayı olma ola- c : 1 2 sılığı nedir? 07 ) Yandaki şekilde A kentinden B kentine en kısa yoldan gitmek üzere hareket eden bir aracın MN caddesinden geçme olasılığı nedir? 4 7 si erkektir. Kız öğrenci- lerin 3 ü , erkek öğrencilerin yarısı matematik dersinden başarı4 lıdır. Bu sınıftan seçilecek bir öğrencinin kız veya matematikten başarılı olma olasılığı kaçtır? 5 c : 7 19 ) bir yarışmada yarışacak üç kişiden birinci kişinin kazanma olasılığı ikinci kişinin 3 katı, ikinci kişinin kazanma olasılığı ise üçüncü kişinin 2 katıdır. Buna göre bu yarışmayı birinci veya ikinci kişinin kazanma olasılığı kaçtır?( birden fazla kişinin kazanma 8 durumu söz konusu değildir.) c: 9 20 ) bir torbada beyaz, mavi ve yeşil toplardan 3 er tane vardır. Bu torbadan rasgele alınan 3 topun aynı renk olma olasılığı ne 1 dir? c: 28 21 ) KÜLTÜR kelimesinin harflerinin yerleri değiştirilerek oluşturulan anlamlı veya anlamsız kelimelerden seçilen kelimenin K veya R den herhangi biri ile başlayıp diğeriyle bitme olasılığı ne- c : 151 22 ) hilesiz bir madeni para 3 kez atıldığında en az bir kez tura 08 ) A 2,3, 4,5 kümesinin elemanları kullanılarak rakamları farklı 4 basamaklı sayılar yazılıyor. Bu sayılardan seçilen bir sayının 5 ile bölünebilme olasılığı nedir? c : 14 09 ) A kümesi tüm rakamlardan oluşan bir küme olmak üzere A kümesinden rasgele seçilen 3 elemanın çarpımının çift sayı olma 11 olasılığı kaçtır? c : 12 10 ) 2 den farklı 4 asal ve 5 çift tamsayı arasından seçilen iki sayı 5 nın toplamının tek olma olasılığı kaçtır? c: 9 11 ) 1, 2,3, 4,5, 6, 7,8,9 kümesinin elemanları kullanılarak yazılabilen rakamları birbirinde farklı üç basamaklı doğal sayılar arasından seçilen bir sayının rakamları çarpımının tek sayı olma c : 425 olasılığı nedir? olasılığı nedir? c :1 35 3 36 24 ) 0, 1, 2, 3, 4, 5 rakamları kullanılarak yazılabilen tüm 4 basamaklı sayılar kağıtlara yazılarak bir torbaya atılıyor. Torbadan herhangi bir kağıt çekildiğinde bu sayının tersinden de okunduğunda aynı sayı olma olasılığı nedir? c : 361 25 ) 33 kişilik bir sınıfta matematik dersinden geçen 17, Türkçe dersinden gecen 24 ve her iki dersten geçen 8 kişi vardır. Sınıftan rasgele seçilen birinin Türkçe dersinden geçtiği bilindiğine c : 13 göre matematik dersinden geçme olasılığı nedir? 26 ) A 1, 2,3, 4,5,6 kümesinin elemanları kullanılarak 3 basa- 27 ) Yandaki şekilde seçilen bir üçgenin A noktasını köşe kabul eden bir üçgen olma olasılığı kaçtır? c : 32 49 c : 110 13 ) iki torbadan birincisinde 2 kırmızı 4 mavi ikincisinde 3 kırmızı 5 mavi bilye vardır. birinci torbadan rasgele seçilen bir top ikinci torbaya atılıyor ve ikinci torbadan bir top çekiliyor. Buna göre ikinci torbadan çekilen topun mavi gelme olasılığı nedir? 17 27 14 ) Yarıçapı 4 cm olan bir dairenin içinde alınan bir noktanın merkeze uzaklığı 3 cm den kısa olma olasılığı nedir? 7 c : 8 23 ) bir çift zar art arda üç kez atılıyor. En az bir kez (6 , 6) gelme gelme olasılığı kaçtır? maklı farklı doğal sayılar elde ediliyor. Seçilen bir sayının en az c : 94 iki basamağının aynı olma olasılığı kaçtır? 12 ) 1. Torbada 5 sarı 6 kırmızı bilye, 2. torbada 4 sarı 5 kırmız bilye vardır. 1. torbadan bir bilye çekilerek 2. Torbaya atılıyor. 2. Torbadan çekilen c : 169 15 ) bir ayrıtının uzunluğu 4 cm olan bir küpün içinde alınan bir noktanın küpün ağırlık merkezine olan uzaklığının en çok 1 cm olma olasılığı nedir? 18 ) 28 kişilik bir sınıftaki öğrencilerin dir? c : 212 bilyenin sarı olma olasılığı nedir? Üzerindeki sayıların toplamının 10 olma olasılığı kaçtır? c : 110 10 c : 48 16 ) her biri 5 seçenekli 10 sorudan oluşan bir sınavda soruların tamamı cevaplandırılacaktır. Her bir soruda bir seçeneği rasgele işaretleyen bir kişinin tüm soruları doğru cevaplandırma olasılığı 1 nedir? c : 10 5 17 ) 10 torbanın her birinde üzerinde 1 den 10 a kadar numara yazılı 10 ar tane bilye vardır. Her birinden birer bilye alınıyor. 28 ) şekildeki dairelerin yarıçapları sırasıyla r1 , r2 ve r3 tür. Yarıçaplar arasında r1 4 r2 3 r3 2 eşitliği olduğuna göre daire- lerin içinde seçilen bir noktanın r2 c : 299 29 ) bir zar ve bir madeni para birlikte atılıyor. zarın tek asal sayı 1 ve paranın tura gelme olasılığı kaçtır? c : 6 yarıçaplı dairenin içinde olma olasılığı kaçtır? 30 ) bir çift zar atılması deneyinde üst yüze gelen sayılar toplamı c : 185 nın 8 den büyük olma olasılığı kaçtır? 31 ) bir zar ard arda iki sefer atılıyor. zarlardan birinin üst yüzüne tek diğer zarın üst yüzüne çift gelme olasılığı kaçtır? c : 14 32 ) bir zar ard arda iki sefer atılıyor. zarın üst yüzüne birincisinde c : 14 çift ikincisinde tek sayı gelme olasılığı kaçtır? 33 ) bir kutuda 5 beyaz 15 kırmızı olmak üzere toplam 20 top vardır. Bu kutudan ard arda çekilen iki topun ikisinin de kırmızı ol21 ma olasılığı kaçtır? c : 38 34 ) bir grupta 4 erkek ve 3 bayan vardır. Bu gruptan seçilecek iki 1 kişinin ikisinin de bayan olma olasılığı kaçtır? c : 7 35 ) bir torbada 5 kırmızı 4 mavi bilye vardır. Torbadan rasgele seçilen 3 bilyeden 2 sinin kırmızı birinin mavi olma olasılığı kaç10 tır? c : 21 36 ) 3 mektup 4 posta kutusuna rasgele atılıyor. mektupların her birinin farklı posta kutularına atılmış olma olasılığı kaçtır? c : 83 37 ) 3,5,7,9,11,15,17 sayılarından seçilen iki sayının toplamı- 51 ) 20 kişilik bir arkadaş grubunda satranç oynayanların sayısı 11 tavla oynayanların sayısı 9 dur. 7 kişi her ikisini de oynadığına göre bu gruptan rasgele seçilen birisinin satranç veya tavla oynama olasılığı kaçtır? c : 13 20 52 ) bir torbada 11 farklı renkte ve her renkten 2 şer adet top bulunmaktadır. Bu torbadan rasgele iki top seçildiğinde ikisinin de aynı renkte olma olasılığı kaçtır? c : 211 53 ) şekildeki çemberin üzerinde 7 nokta vardır. Bu noktalar kullanılarak çizilebilecek tüm doğrulardan rasgele bir doğru seçildiğinde bu doğrunun D noktasından geçme olasılığı kaçtır? c : 72 c : 17 38 ) iki kutudan birisinde 7 tane 10 krş 2 tane 1 tl, ikincisinde 4 tane 10 krş 3 tane 1 tl vardır. Birinci kutudan rasgele bir madeni para çekilip ikinci kutuya atılıyor. ikinci kutudan rasgele alınan 29 bir paranın 1 tl olma olasılığı kaçtır? c : 72 54 ) bir para ard arda 4 kez havaya atılıyor. en çok 3 kez yazı gel15 me olasılığı kaçtır? c : 16 39 ) bir torbada 3 sarı 4 kırmız bilye vardır. Bu torbadan rasgele c : 17 seçilen 3 bilyenin aynı renkte olma olasılığı kaçtır? 56 ) bir araba yarışında 3 araba yarışmaktadır. Birincinin kazanma şansı ikincinin kazanma şansının 15 katı, ikincinin kazanma nın 20 olma olasılığı kaçtır? 40 ) 1 den 9 a kadar dokuz rakam kullanılarak yazılabilen rakamları tekrarsız tüm üç basamaklı sayılar birer karta yazılıp bir torbaya atılıyor. rasgele torbadan bir kart seçildiğinde üzerindeki c : 281 sayıların rakamları toplamının 9 olma olasılığı kaçtır? 41 ) bir sınıftaki 12 kızın 4 ü gözlüklü, 8 erkeğin ikisi gözlüklüdür. sınıftan rasgele seçilen birisinin kız veya gözlüklü olma olasılığı c : 107 kaçtır? 42 ) 12 erkek ve 8 kadın arasından 3 kişi rasgele seçiliyor. Seçilen 11 3 kişinin de erkek olma olasılığı kaçtır? c : 57 43 ) 4 evli çift arasından seçilen 2 kişinin birisinin bayan birisinin c : 74 erkek olma olasılığı kaçtır? 44 ) şekilde verilenlere göre x tamsayısının çift tamsayı olma olasılığı kaçtır? c : 73 55 ) özgür ile rüyanın da aralarında bulunduğu 8 kişi arasından 4 kişilik bir grup oluşturulacaktır. Bu grupta özgürün bulunup rüyanın bulunmama olasılığı kaçtır? c : 72 şansı üçüncünün kazanma şansının 1 3 katı ise üçüncünün ka- 5 c : 7 57 ) %40 ı bayan. %60 ı erkek olan bir toplulukta bayanların 14 ü zanma şansı kaçtır? ve erkeklerin 1 2 si gözlük kullanmaktadır. Topluluktan rasgele seçilen bir kişinin erkek veya gözlük kullanan bir kişi olma olasılıc : 107 ğı kaçtır? 58 ) A ve B aynı örnek uzaya ait iki olay olmak üzere P A P B ' 13 ve P A B 3 4 ise P A B ? 1 2 c : 125 59 ) A ve B aynı örnek uzayda iki olay olmak üzere P A B 15 , P A B 157 , P B P A 154 ise P A kaçtır? 60 ) A ve B aynı örnek uzayın iki olayı, P A B 13 20 1 c : 5 ve P A ' 53 ise P (A\B) olasılığı kaçtır? 45 ) üç zar birlikte atılıyor. zarlardan ikisinin aynı birinin farklı ve üste gelen sayıların toplamının 13 olma olasılığı kaçtır? c : 241 46 ) bir atıcının hedefi vurma olasılığı 1 4 tür. Bu atıcı 3 atış yap- tığında herhangi birisini kaçırıp diğer ikisini vurma olasılığı kaçc : 649 tır? 47 ) üç basamaklı rakamları birbirinden farklı olan tüm doğal sayılar ayrı ayrı kağıtlara yazılıp bir torbaya atılıyor. daha sonra bu sayılar içinden rasgele bir sayı seçiliyor. Seçilen bu sayının en az 25 c : 27 bir basamağının tek olma olasılığı nedir? 48 ) 0 dan 99 a kadar ( 0 ve 99 dahil ) numaralandırılmış 100 kart bir torbaya konuluyor. Bu torbadan rasgele iki kart aynı anda çekiliyor. Çekilen kartların üzerindeki sayıların çarpımının c : 149 çift sayı olma olasılığı kaçtır? 198 49 ) 6 siyah 4 beyaz topun bulunduğu bir torbadan rasgele çekilen üç topun siyah gelme olasılığı, çekilen topu geri atmamak koşuluyla ard arda çekilen iki topun beyaz gelme olasılığından c : 301 ne kadar fazladır? 50 ) Düz bir zemine bir kalıp peynir, peynirden 1 metre uzağa herhangi bir yere siyah fare. Siyah fareden 1 metre uzağa herhangi bir yere beyaz fare konuyor. Buna göre siyah farenin peynire beyaz fareden daha önce ulaşma olasılığı kaçtır? c : 32 1 c : 4 61 ) A, B ve C kümeleri ayrık ve A B C E dir. Buna göre P A 13 , P C 53 ise P B ? 1 c : 15 62 ) Bir sınıftaki öğrencilerin %60 matematik %30 kimya, %20 si ise her iki dersten geçmiştir. Bu sınıftan seçilen bir öğrencinin kimyadan geçtiği bilindiğine göre matematikten kalmış olma 1 olasılığı nedir? c: 3 63 ) hilesiz bir çift zar atılıyor. zarlardan birinin 4 geldiği biliniyor. Üst yüze gelen sayılar toplamının 9 olma olasılığı kaçtır? c : 112 64 ) 50 kişilik bir sınıftaki öğrencilerin her biri Türkçe veya matematik derslerinin en az birinden geçmiştir. 30 kişi matematikten 27 kişi Türkçeden geçtiğine göre seçilen bir öğrencinin matematikten geçtiği biliniyorsa bu öğrencinin türkçeden geçme olasılığı c : 307 kaçtır? 65 ) bir tiyatro salonundaki izleyicilerden %30 u uzun boylu %20 si sarışın ve %10 u hem uzun boylu hemi de sarışındır. Oyun arasında giden bir izleyicinin uzun boylu olduğu bilindiğine göre c : 13 sarışın olma olasılığı kaçtır? 66 ) iki zar atılıyor. zarların üst yüzüne gelen sayıları tek olduğu c : 94 bilindiğine göre ikisinin de asal olma olasılığı kaçtır?