01 ) ortak bölenlerinin en büyüğü 30 olan birbirinden farklı iki doğal

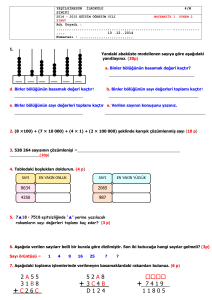
01 ) ortak bölenlerinin en büyüğü 30 olan birbirinden
farklı iki doğal sayının toplamı en az kaçtır? c : 90
02 ) ortak katlarının en küçüğü 20 olan birbirinden
farklı üç sayının toplamı en fazla kaçtır? c : 35
03 ) 180 ve 240 sayıları hangi sayı ile bölünürse elde
edilen bölümler toplamı en az olur?
c : 60
04 ) 65 kişilik bir öğrenci grubuna en az kaç öğrenci
ilave edelim ki bu öğrenciler 6 ve 9 arlı gruplara
ayrılabilsin.
c : 7
05 ) 281, 322, 363 sayılarını böldüğünde sırasıyla 1, 2
ve 3 kalanını veren en büyük doğal sayı kaçtır? c : 40
06 ) x  3a  1  5b  3  7c  5 olduğuna göre x ’in
alacağı en küçük değer kaçtır?
c : 103
07 ) A ve B doğal sayılarının en büyük ortak böleni 6
dır. 8 A  12B olduğuna göre A + B toplamı kaçtır?
c : 30
08 ) m, n  Z  ve obebm, n  okekm, n  117 ise
m + n kaçtır?
c : 63
09 ) x  y  N , x  y  48 ve obebx, y   6 ise
x  y farkı aşağıdakilerden hangisi olabilir? c : B
A)6
B ) 12
C ) 16
D ) 18
E ) 24
10 ) obeb28, x  4 , okekx,28  84 olduğuna göre
x kaçtır?
c : 12
11 ) Ardışık iki doğal sayının okek ile obeb’inin
toplamı 43 ise bu sayıların toplamı kaçtır? c : 13
12 ) Boyutları 40 m, 50 m ve 20 m olan
dikdörtgenler prizması şeklindeki depo içerisine hiç
boşluk kalmayacak şekilde küp şeklindeki sandıklar
yerleştiriliyor. Buna göre en az kaç sandık gereklidir?
c : 40
13 ) boyutları 60 m ve 70 m olan dikdörtgen
şeklindeki bahçenin çevresine köşeler dahil olmak
üzere eşit aralıklarla ağaçlar dikilecektir. Buna göre en
az kaç ağaç gereklidir?
c : 26
14 ) 30, 45 ve 75 sayılarına tam bölünen üç basamaklı
en büyük doğal sayı kaçtır?
c : 900
15 ) 175 ve 300 sayılarını aynı doğal sayı ile tam
bölündüğünde elde edilen bölümler toplamı en az kaç
olur?
c : 19
16 ) farklı iki doğal sayının okek’i 45 olduğuna göre
toplamları en çok kaç olabilir ? c : 60
17 ) iki doğal sayının en küçük ortak katı 30 olduğuna
göre bu iki sayının toplamı en az kaçtır?
c : 11
18 ) obebx, y   7 ve 6 x  9 y ise x  y  ? c : 7
19 ) Ahmet bilyelerini sekizerli ve dokuzarlı gruplara
ayırdığında her seferinde üç bilyesi artmaktadır. Buna
göre Ahmet ’in en az kaç bilyesi vardır? c : 75
20 ) 320, 428 ve 550 sayılarını böldüğünde sırasıyla
20, 8 ve 10 kalanlarını veren en büyük doğal sayı
kaçtır?
c : 60

21 ) a, b, c  N ve A  4a  2  5b  3  6c  4
ise x’in alabileceği en küçük değer kaçtır? c : 58
22 ) 420 litre ayçiçek yağı, 482 litre soya yağı ve 540
litre zeytin yağı birbirine karıştırılmadan eşit hacimli
tenekelere boşaltılacaktır. Buna göre en az kaç teneke
gereklidir?
c : 121
23 ) boyutları 8, 10 ve 15 cm olan dikdörtgenler
prizması şeklindeki kutuların en az kaç tanesi ile bir
küp oluşturulabilir?
c : 1440
24 ) üç koşucu sırasıyla 12, 16 ve 24 saniyede dairesel
bir pisti koşabilmektedir. Üç koşucu aynı noktadan
koşmaya başladıktan sonra tekrar bir araya geldiklerinde birinci koşucu pistte kaç tur atmış olur? c : 4
90
25 ) A 
eşitliğinde A doğal sayı olduğuna göre
x
kaç farklı değer alır?
c : 12
26 ) 120’nin tamsayı bölenlerinden kaç tanesi asal sayı
değildir?
c : 29
n
27 ) 16.3 sayısının tamsayı bölenlerinin sayısı 50
olduğuna göre n kaçtır?
c : 4
28 ) 5.72 n sayısının doğal sayı bölenlerinin sayısı
140 olduğuna göre n kaçtır?
c : 3
29 ) 3000
...
0 sayısının 676 tane tamsayı böleni
k .. tan e
olduğuna göre k kaçtır?
c : 12
30 ) 75 sayısı pozitif bir x sayısı ile bölündüğünde 3
kalanını veriyor. Buna göre x kaç farklı değer alır?
c : 9
31 ) a ve b aralarında asal sayılar olmak üzere
16
 41  b ise a = ? c : 8
okeka, b  312 ve
a
x y
32 ) x, y  Z  , 
ve okekx, y   210 ise
5 7
c : 6
obeba, b  ?
33 ) Ardışık iki pozitif çift sayının okek’i 60 olduğuna
göre bu iki sayının toplamı kaçtır?
c : 22

34 ) x, y, z  Z , okekx, y   6 ve okek y, z   9
ise x  y  z toplamı en az kaçtır? c : 33
35 ) A B C
2
D H L 2
E K M 3
F K
1
5
1 K
17
1
ise A + B + C = ? c : 140
36 ) 15 ile bölündüğünde 3, 18 ile bölündüğünde 6
kalanını veren en küçük doğal sayı kaçtır? c : 78
37 ) a, b, c  Z  , x  3a  1  5b  3  7c  5
eşitliğini sağlayan x ’in en küçük değeri kaçtır?
c : 103
38 ) Ali cevizlerini 4 erli, 5 erli ve x erli gruplara
saydığında hep 2 cevizi artıyor. Ali’nin cevizlerinin
sayısı 142 olduğuna göre x ’in en büyük tek sayı
değeri kaçtır?
c : 35
39 ) 3 ve 4 ile bölündüğünde 2 kalanını veren ve 5
ile tam bölünebilen en küçük tamsayının rakamları
toplamı kaçtır?
c : 5
40 ) Kenar uzunlukları 32 m ve 56 m olan
dikdörtgen şeklindeki bahçenin kenarlarına, köşelerine
ve iç kısmına eşit aralıklarla fidan dikilecektir. Buna
göre en az kaç fidan gereklidir?
c : 40
2 4
5
41 ) ,
ve
saat arayla çalan üç zil saat 12 : 00
3 5
6
da birlikte çalıyorlar. Bu ziller tekrar birlikte ilk kez
saat kaçta çalar?
c : 08 : 00
42 ) Üç ülkenin 24, 48 ve 56 kişilik üç sporcu kafilesi
bir otele yerleştirilecektir. Aynı ülkenin sporcularının
aynı odada bulunması ve her odada eşit sayıda kalması
şartıyla 128 kişilik bu üç kafile için en az kaç odaya
ihtiyaç vardır?
c : 16
43 ) dairesel bir pist etrafında yarışan üç araçtan
birincisi 25 dk da, ikincisi 30 dk. da, üçüncüsü 35 dk.
da turunu tamamlamaktadır. Aynı anda aynı noktadan
ve aynı yönde yarışmaya başlayan araçların üçü birden
tekrar aynı noktaya geldiklerinde en yavaş olan araç
kaç tur atmıştır?
c : 30
7x  4
44 )
ifadesi bir asal sayı ise x yerine
x
yazılabilecek kaç farlı tam sayı vardır?
c : 3

x
45 ) x, y  Z ve 21! 3 . y ise x en çok kaç
olabilir?
c : 9
46 ) ortak katlarının en küçüğü, ortak bölenlerinin en
büyüğünden 55 fazla olan ardışık iki doğal sayının
toplamı kaçtır?
c : 15
47 ) a ve b aralarında asal sayılar olmak üzere
315
 a  15 olduğuna göre
okeka, b  210 ve
b
a – b farkı kaçtır?
c : 29
48 ) A  3x  1  4 y  2  5 x  8 eşitliğini sağlayan
en küçük A değeri için y kaçtır?
c : 15
49 ) Bir çoban dürüdeki koyunları 3 er saydığında 2,
beşer saydığında 4, altışar saydığında 5 koyun
artmaktadır. Sürüdeki koyun sayısı 150 den fazla
olduğuna göre en az kaç koyun vardır?
c : 179
50 ) 1802 sayısına en az kaç eklenmelidir ki elde
edilen sayı 2, 5, 6 ve 8 ile tam bölünebilsin. c : 118
51 ) 62, 88 ve 114 sayılarını böldüğünde sırası ile 2,
4 ve 6 kalanlarını veren en büyük doğal sayı katır?
c : 12
52 ) bir otobüs durağındaki üç otobüs sırasıyla 20, 30
ve 45 dakikada servislerini tamamlayıp tekrar servise
çıkmaktadırlar. İlk kalkışlarını sabah 6 : 00 da yapan
bu üç otobüs ikinci kez aynı duraktan aynı anda saat
kaçta servis yapmak üzere kalkarlar.
c : 9 : 00
x
53 ) 9.5 sayısının 30 tane tam böleni olduğuna göre
x kaçtır?
c : 4
54 ) obeb40,60,80  ?
c : 20
55 ) a, b, c  Z  , 59  ax  3 , 88  bx  4 ,
117  cx  5 ise x ’in en büyük değeri kaçtır? 28
56 ) okek24,54  ?
c : 216
57 ) ardışık iki doğal tek sayının okek ile obeb leri
çarpımı 99 ise bu iki sayının toplamı kaçtır? c : 20
58 ) bir sepetteki güllerden 6 şarlı ve 8 erli demetler
yapıldığında hiç gül artmamaktadır. Buna göre sepette
en az kaç gül vardır?
c : 24
59 ) kenar uzunlukları 8 m ve 12 m olan dikdörtgen
şeklindeki bir salon kare şeklindeki fayanslarla kaplanacaktır. Buna göre en az kaç fayans gereklidir? c : 6
60 ) xx iki basamaklı bir doğal sayıdır. Buna göre
xx2  x 2 sayısı hangisi ile tam bölünemez? c : E
A ) 30 B ) 35 C ) 36 D ) 135 E ) 165
61 ) xy3z sayısı 12 ye bölündüğünde 3 kalanını
veren rakamları farklı dört basamaklı bir sayıdır. Buna
göre x + y + z toplamının en büyük değeri kaçtır?
c : 24
62 ) x bir tamsayı olmak üzere 36.2 x sayısının asal
olmayan tamsayı bölenlerinin sayısı 40 olduğuna göre
x kaçtır?
c : 4
63 ) Bir bahçıvan çiçeklerini 5 er sayarsa 3, 6 şar
sayarsa 4 çiçek eksik kalıyor. 7 şer sayarsa 2 çiçek
artıyor. Çiçek sayısı 500 den az olduğuna göre en çok
kaç çiçek vardır?
64 ) 4 x  y ve 3x  y sayılarının obeb’i 4 ve
4 x  y 27
ise x kaçtır?

c : 8
3x  y 21
65 ) x ve y aralarında asal sayılar olmak üzere
100
 xy  obebxy  205 ise
okekx, y   200 ,
x
x + y toplamı kaçtır?
c : 33
66 ) 9!8! , B  9!8.8! , C  8.7!8! olduğuna göre
c : 10.8!
okek A, B, C   ?
67 ) 705 sayısına en az kak eklenirse elde edilen sayı
12, 15, 18 ile tam bölünür?
c : 15

68 ) x, y, z  z , x > 45 ve x  4 y  1  5 z  3 ise
x en az kaçtır?
c : 63
3
69 ) obeb24, x,60  6 , okekx,24,60  2 .3.5 2 ise
x en az kaçtır?
c : 150
70 ) 45, 72 ve x litrelik 3 bidon üç farklı sıvı ile
doludur. Şişeler birbirine karıştırılmadan en büyük ve
eşit hacimli 20 şişeye hiç artmayacak şekilde dolduruluyor. Buna göre x kaçtır?
c : 63
71 ) boyutları 90 cm, 105 cm, 135 cm olan bir depo
hacmi en büyük olan küp şeklindeki kutularla
doldurulacaktır. En az kaç kutu gereklidir?
c : C
72 ) Kenarları 96 m ve 168 m olan dikdörtgen
şeklindeki parsellere ayrılacak ve her parselin dört
köşesine birer kazık çakılacaktır. Bunun için kaç kazık
gereklidir?
c : 40
73 ) Ayrıt uzunlukları 2 cm, 6 cm ve 10 cm olan
dikdörtgenler prizması şeklindeki kutular ile küp
yapılmak istense en az kaç kutuya ihtiyaç vardır?
c : 225
74 ) okek15,24  obeb15,24  ?
c : 123
75 ) 12 ve 18 i tam bölen kaç doğal sayı vardır?
c : 4
76 ) 5 ile bölündüğünde 4, 8 ile bölündüğünde 2
kalanını veren iki basamaklı en küçük doğal sayı
kaçtır?
c : 34
77 ) 6 ve 15 ’e bölündüğünde 4 kalanını veren en
küçük pozitif tamsayı kaçtır?
c : 34
78 ) kenar uzunlukları 70 m ve 80 m olan dikdörtgen
şeklindeki bir bahçenin etrafına eşit aralıklarla fidan
dikilecektir. Köşelerde fidan olmak şartıyla en az kaç
fidana ihtiyaç vardır?
c : 30
79 ) iki kaptan birinde 60 litre sirke, diğerinde 84 litre
yağ bulunmaktadır. Yağ ve sirke birbirine karıştırılmamak ve hiç arttırmamak şartı ile eşit hacimdeki
şişelere doldurulacaktır. Bunun için en az kaç şişeye
ihtiyaç vardır?
c : 12
80 ) kenar uzunlukları 72 m ve 90 m olan dikdörtgen
şeklindeki bir duvara kare şeklindeki özdeş fayanslar
ile döşenecektir. Bu iş için en az kaç fayansa ihtiyaç
vardır?
c : 20
81 ) Kenar uzunlukları 72 cm ve 152 cm olan
dikdörtgen şeklindeki bir levhadan birbirine eş en az
kaç tane kare levha elde edilir?
c : 171
82 )
01 ) obeb3a  b, a  2b  1 olmak üzere
3a  b 6

ise a.b çarpımı kaçtır?
c : 6
a  2b 16
02 ) a  b ve a ile b ardışık iki çift doğal sayıdır.
obeba, b.okeka, b  168 ise a + 2b toplamı
kaçtır?
c : 40
03 ) Kenar uzunlukları 96 m ve 120 m olan dikdörtgen şeklindeki idman sahasının etrafına ve köşelerine
eşit aralıklarla aydınlatma direkleri dikilecektir. Buna
göre en az kaç direğe ihtiyaç vardır?
c : 18
04 ) obeba,45  5 ve okek45, a   225 ise a ayısı
kaçtır?
c : 25
05 ) Kenar uzunlukları 80 m ve 128 m olan dikdörtgen şeklindeki bir bahçenin etrafına ve köşelerine eşit
aralıklarla ağaç dikilecektir. Buna göre en az kaç ağaca ihtiyaç vardır?
c : 26
06 ) kenar uzunlukları 3 m ve 5 m olan dikdörtgen
şeklindeki levha boyutlarına bakılmaksızın en az kaç
tane kare şeklindeki levhaya ayrılabilir?
c : 15
07 ) okek45,81, a  1215 olduğuna göre a sayısı en
az kaçtır?
c : 243
08 ) okek i 12 olan farklı üç doğal sayının toplamı en
az kaçtır?
c : 72
09 ) x ve y ardışık iki sayı olmak üzere
c : 17
obebx, y .okekx, y   72 ise x + y = ?
10 ) 18, 27 ve 45 kg lık üç ayrı cins kömür birbirine
karıştırılmadan hiç artmayacak şekilde eşit ağırlıkta
poşetlere konulacaktır. Buna göre en az kaç poşete ihtiyaç vardır?
c : 10

11 ) a, b, c  Z , x  3a  2  5b  4  9c  8 ise x
in üç basamaklı en küçük tamsayı değeri için a + b
toplamı kaçtır?
c : 70
12 ) toplamları 34 olan a ve b pozitif tamsayılarının
en küçük ortak katı 273 tür. Buna göre a  b farkı
kaçtır?
c : 8
13 ) a, b, c birbirinden farklı sayma sayılarıdır.
okeka, b, c  250 ise a + b + c toplamının en büyük değeri kaçtır?
c : 425
a
 4 ise
14 ) okeka  b,2a  2b  2a 2  2b 2 ve
b
b kaçtır?
c : 1
15 ) x, y   1 ve okekx, y   42 ve x. y  4  14
ise x kaçtır?
c : 7
16 ) bir bakkalda bulunan sabunlar 3 er, 6 şar ve 7
şer sayıldığında sırasıyla 1, 4 ve 5 sabun artmaktadır.
Bakkaldaki sabun sayısı üç basamaklı olduğuna göre en
az kaç sabun vardır?
c : 124

17 ) x, y, z  Z , A  5 x  4  7 y  6  11z  1 ise
A nın en küçük tamsayı değeri kaçtır?
c : 384
3 2
4
18 )
,
ve
sayılarına bölündüğünde tamsayı
10 3
5
sonuç veren en küçük doğal sayının rakamları toplamı
kaçtır?
c : 3
20
19 ) a, b, c farklı asal sayılar olmak üzere a 
bc
ise a + b + c toplamı kaçtır?
c : 12
20 ) 1 den büyük asal olmayan bir tamsayının rakamlarının toplamı, asal sayı çarpanlarına ayrılarak yazıldığında bu yazılışta bulunan tüm asal sayıların rakamlarının toplamına eşit oluyorsa bu tür sayılara smith sayısı denir. Örneğin 27 sayısı asal çarpanlarına
27 = 3.3.3 şeklinde ayrılır. 2 + 7 = 3 + 3 + 3 olduğundan 27 sayısı bir simith sayısıdır. Buna göre
aşağıdakilerden hangisi bir simith sayısıdır?
c : B
A ) 102 B ) 121 C ) 144 D ) 150 E ) 185
21 ) 60 kg, 84 kg ve x kg ağırlığındaki 3 ayrı cins
pirinç birbirine karıştırılmadan eşit ve en büyük ağırlıkta olacak şekilde 21 poşete konulabiliyor. Buna
göre x kaçtır?
c : 108
22 ) x ve y pozitif tamsayılarının en büyük ortak böleni 1 dir. x.y = 700 olduğuna göre kaç farklı x, y 
ikilisi yazılabilir?
c : 8
x y

23 ) x, y  Z  ,
ve okekx, y   126 ise
3 7
x + y toplamı kaçtır?
c : 60
24 ) x, y  Z  olmak üzere x  17  a 5 , y  a 5  3
olduğuna göre x.y çarpımının alabileceği en büyük
değer kaçtır?
c : 49
b
0
25 ) a, b, c  R ve a 3 b 4 c  0 , abc  0 ve
c
ise a, b ve c nin işaretleri nasıldır?
c : ,,
26 ) ardışık iki pozitif tek sayının kareleri farkı 120
ise bu sayılardan küçük olanı kaçtır?
c : 29
a 3

27 ) a, b  N ,
ve obeba, b  5 ise
b 7
c : 105
okeka, b kaçtır?
28 ) 1700 sayısına en az kaç eklenmelidir ki elde edilen sayı 3, 7 ve 11 ile bölündüğünde 2 kalanını
versin.
c : 150
29 ) x, y  N olmak üzere 2 x  5 y  54 eşitliğini
sağlayan y değerleri toplamı kaçtır?
c : 30
30 ) n bir sayma sayısı olduğuna göre aşağıdakilerden
hangisi daima çift sayıdır?
c : B
n
n
4
3
A ) n!n  1
B ) 2  3 1 C ) n  n 1
5
D ) n  n4 1
E ) n  1!n!1
31 )  28,23,18,........,37,42,47 dizisinin terim sayısı x, bu dizideki terimlerin toplamı y ise y – x farkı
kaçtır?
c : 136
32 ) üç basamaklı bir sayı ilk iki rakamından oluşan
sayı ile son iki rakamından oluşan sayının toplamının
iki katına eşittir. Buna göre bu üç basamaklı sayının
rakamları toplamı kaçtır?
c : 15
33 ) a, b, c birbirinden farklı rakamlar olmak üzere
a 2  b.c koşulunu sağlayan kaç farklı abc sayısı
yazılabilir?
c : 8
34 ) x, y  Z  , x, y   1 ve x + y = 24 ise kaç
farklı x, y  ikilisi vardır?
c : 8
a 1 3

35 ) obeb(a  1, b  4)  4 ,
ise a  b  ?  43
b4 7