Genel Enerji Denklemi Genel Enerji Denklemi
advertisement

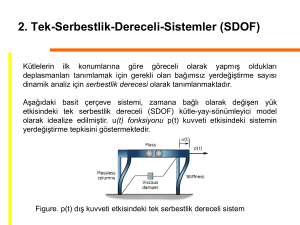
KÜTLE, BERNOULLI VE ENERJİ DENKLEMLERİ BU KONU TAMAMLANDIĞINDA; -BİR AKIŞ SİSTEMİNDE GİREN VE ÇIKAN DEBİLERİ DENGELEYEBİLMEK İÇİN KÜTLE DENKLEMİNİ UYGULAYABİLMELİSİNİZ -MEKANİK ENERJİNİN FARKLI FORMLARINI TANIYABİLMELİ VE ENERJİ DÖNÜŞÜM VERİMLERİYLE İLGİLİ İŞLEMLERİ YAPABİLMELİSİNİZ -BERNOULLİ DENKLEMİNİN KULLANIMINI VE SINIRLAMALARINI ANLAYABİLMELİ VE BU DENKLEMİ FARKLI TÜRLERDEKİ AKIŞ PROBLEMLERİNİ ÇÖZMEDE KULLANABİLMELİSİNİZ -YÜKLER CİNSİNDEN İFADE EDİLEN ENERJİ DENKLEMİYLE ÇALIŞABİLMELİ VE BU DENKLEMİ TÜRBİN ÇIKIŞ GÜCÜNÜ VE GEREKLİ POMPALAMA GÜCÜNÜ HESAPLAMADA KULLANABİLMELİSİNİZ Kontrol Hacmi İçin Kütle ve Enerjinin Korunumu mgiren - mçıkan Kütle korunumu: dmKH = dt Enerjinin korunumu: Egiren - Eçıkan Isı,İş ve Kütleile birim zamanda transfer edilen net enerji = dEKH dt İç,Kinetik,Potansiyel, vb enerjilerinin toplmanın birim zamandaki değişimi KÜTLESEL VE HACİMSEL DEBİ, ORTALAMA HIZ Kütlesel debi: m= ò dm = ò r Vn dAc Ac Ortalama hız: kg/s Ac Vort 1 = Ac ò Vn dAc Ac Hacimsel debi: V = ò r Vn Ac = Vort Ac = VAc Ac Ortalama hız cinsinden kütlesel debi: m = r Vort Ac = rV m3 /s dm = r Vn dAc KÜTLENİN KORUNUMU DENKLEMİ Kütlenin korunumu yasası, Reynolds transport teoremindeki B değişkenini kütle m ile, b değişkenini de 1 (birim kütle için kütle=m/m=1) ile yer değiştirerek elde edilir. d r dV + ò dt KH ò r (V ×n)dA = 0 KY Üniform giriş ve çıkış hızları söz konusu ise , dmKH dt å giriş m+ å çıkış m= 0 Hareket eden veya şekil değiştiren kontrol hacmi: d r dV + ò dt KH ò r (Vb ×n)dA = 0 KY Vb = V - VKY Daimi akış: å m= giren Bir giriş bir çıkış varsa: å m çıkan m = r 1V1 A1 = r 2V2 A2 Bu ifadeye SÜREKLİLİK DENKLEMİ denir. Sıkıştırılamaz akış halinde yoğunluk değişmediğinden, SÜREKLİLİK DENKLEMİ: å V = giren å V ® Tek akımlı: çıkan V1 = V2 ® V1 A1 = V2 A2 ÖRNEK 5-1 Ağzına fıskiye takılmış bir bahçe hortumu 10 galon’luk (37.854 L) bir kovayı suyla doldurmak için kullanılıyor. Borunun iç çapı 2 cm olup fıskiye çıkışında çap 0.8 cm’ye düşüyor (Şekil 5-12). Kovayı suyla doldurmak 50 s aldığına göre; (a) hortumdan geçen suyun kütlesel ve hacimsel debilerini ve (b) fıskiye çıkışında suyun ortalama hızını hesaplayınız. V = V 37.854 = = 0.757L/s Dt 50s m = rV = (1kg/L)(0.757 L/s) = 0.757 kg/s 2 Aç = p rç2 = p (0.4cm) = 0.5027cm2 = 0.5027x10- 4 m2 æ 1m3 ÷ ö V 0.757 L/s ç ÷ ç Vç = = = = 15.1m/s ÷ ç - 4 2 ÷ çè1000L ø Aç 0.5027x10 m ÖRNEK 5-2 0.914 m çapında, 1.219 m yüksekliğinde ve üst yüzeyi atmosfere açık silindirik bir tank başlangıçta suyla doludur. Tankın taban kenarında bulunan boşaltma tapası çekiliyor ve su 1.27 cm çapındaki bir su jeti ile dışarı fışkırıyor (Şekil 5-13). Su jetinin ortalama hızı V= 2 gh bağıntısıyla verilmektedir. Burada, h tank içindeki suyun delik merkezinden olan yüksekliği (değişken), g ise yerçekimi ivmesidir. Tank içindeki su seviyesinin tabandan itibaren 0.609 m yüksekliğe düşmesi için geçecek olan süreyi hesaplayınız. ÇÖZÜM Tankın iç hacmini KH olarak seçelim. Bu durumda KH sabit ve şekil değiştirmeyen bir KH olur. Ancak suyun boşalmasından ötürü KH içerisindeki su zamanla değişir. Kütlenin korunumu yasası: mgiren - mçıkan = dmKH dt mçıkan = (r VA)çıkan = r 2 ghAjet ( ) 2 mKH = rV = r Atank h = r p Dtank /4 h - r 2 gh Ajet = ò0 dt = - t= dt ( /4 = dt = - 2 Dtank 2 Djet - r 2 gh t d (r Atank h) 2 Dtank 2 Djet 2 p Djet 1 ) h2 ò 2 g h0 ( ) 2 r p Dtank / 4 dh dt dh 2 gh dh h Þ t= 2 æ ö h0 - h2 ç Dtank ÷ ÷ çç ÷ ÷ g 2 çè Djet ÷ ø 2 æ ö 1.219 m - 0.609 m ç91.4cm ÷ ÷ = 757s = 12.6dakika çç ÷ ÷ è1.27 cm ø 9.81 m/s2 / 2 İrdemele: h2 = 0 alınarak tankın tankın tamamının boşalması için gerekli süre hesaplanabilir. Bu yapılırsa t = 43.1 dakika olarak bulunur. Viskoz etkiler ihmal edildiğinden gerçek süre burada hesaplananlardan daha yüksek olacaktır. Uyarı: Burada yapılan hesaplamada tank kesiti sabittir. Kesit alanı yükseklikle değişen tanklarda kesit alanının yüksekliğe bağlı ifade edilmesi koşuluyla aynı analiz değişken kesitli tanklarda da yapılabilir. Değişken kesite örnekler. MEKANİK ENERJİ VE VERİM Mekanik enerji, ideal türbin gibi ideal mekanik makinalar ile tamamen ve doğrudan mekanik işe dönüştürülebilen enerji formu olarak tanımlanabilir Akmakta olan akışkanın mekanik enerjisi emek P V2 = + + gz J/kg r 2 Mekanik enerji değişimi: D emek P2 - P1 V22 - V12 = + + g ( z2 - z1 ) kJ/kg r 2 Isı (veya termal) enerji doğrudan ve tamamen mekanik işe dönüştürülemediğinden mekanik enerji DEĞİLDİR. BİR TÜRBİNDEN ELDE EDİLEBİLECEK MAKSİMUM İŞ Atmosferik basınç D emek P2 - P1 V22 - V12 = + + g ( z2 - z1 ) kJ/kg r 2 giriş-çıkış kesitleri aynı Giriş-çıkış yükseklik değişimi önemsiz Bu denklemden sonuç negatif çıkar, neden? SONUÇ: Akış hızında ve yükseklikte herhangi bir değişiklik olmaması halinde, ideal bir hidrolik türbinde üretilen güç türbindeki basınç düşüşü ile orantılıdır. BİR DEPODAKİ SUYUN MEKANİK ENERJİSİ Bir deponun tabanındaki suyun mekanik enerjisi, deponun serbest yüzeyi de dahil olmak üzere herhangi bir derinlikteki mekanik enerjisine eşittir. MEKANİK VERİM TANIMI hmek Emek, kayıp Emek, alınan Alınan mekanik enerji = = = 1Verilen mekanik enerji Emek, verilen Emek, verilen Bir fanın mekanik verimi, havanın fan çıkışındaki kinetik enerjisinin verilen mekanik enerjiye oranıdır. BİR POMPANIN VERİMİ hpompa Akışkanın mekanik enerjisindeki artış D Emek,akışkan Wpompa, f = = = Verilen mekanik enerji Wmil, giren Wpompa D Emek, akışkan = Emek, çıkan - Emek, giren BİR TÜRBİNİN VERİMİ htürbin Wmil, çıkan Wtürbin Alınan mekanik enerji = = = Akışkanın mekanik enerjisindeki azalma Wtürbin, ç D Emek, akışkan D Emek, akışkan = Emek, giren - Emek, çıkan MEKANİK VERİM ile MOTOR/JENERATÖR VERİMİ karıştırılmamalıdır. ELEKTRİK MOTORUNUN VERİMİ hmotor Wmil, çıkan Alınan mekanik güç = = Verilen elektriksel güç Welekt, giren JENERATÖR VERİMİ h jeneratör Alınan elektriksel güç Welekt, çıkan = = Verilen mekanik güç Wmil, giren MAKİNA GRUPLARININ VERİMİ, AYRI AYRI VERİMLERİN ÇARPIMINA EŞİTTİR. POMPA-MOTOR GRUBUNUN VERİMİ: hpompa-motor = hpompa hmotor = Wpompa, f Welekt, giren = D Emek, akışkan Welekt, giren TÜRBİN-JENERATÖR GRUBUNUN VERİMİ: htürbin-jen = htürbin h jen = Welekt, çıkan Wtürbin, ç = Welekt, çıkan D Emek, akışkan Türbin-jeneratör grubunun toplam verimi, türbin verimi ile jeneratör veriminin çarpımıdır ve akışkanın mekanik enerjisinin elektrik enerjisine dönüşüm oranını gösterir. ÖRNEK 5-3 Büyük bir göldeki su, bir hidrolik türbin-jeneratör düzeneğini Şekil 5-18’de gösterildiği gibi su derinliğinin 50 m olduğu bir yere yerleştirmek suretiyle elektrik üretmek için kullanılacaktır. Su, türbine 5000 kg/s’lik bir kütlesel debi ile girmektedir. Üretilen elektrik gücü 1862 kW olarak ölçüldüğüne ve jeneratör verimi yüzde 95 olduğuna göre (a) türbin-jeneratör düzeneğinin toplam verimini, (b) türbinin mekanik verimini, (c) türbinden jeneratöre verilen mil gücünü hesaplayınız. ÇÖZÜM 5-3 Kabuller 1 Göldeki su seviyesi değişmemektedir. 2 Türbin çıkışındaki suyun mekanik enerjisi ihmal edilebilir Referans düzlemi gölün tabanı alındığında türbinin girişi ile çıkışı arasında suyun mekanik enerjisindeki değişim: emek,giren - emek,çıkan æ 1kJ/kg ö P ÷ 2 ÷ = - 0 = gh = 9.81m/s (50 )ççç = 0.491 kJ/kg ÷ 2 2 ÷ ç r è1000 m /s ø ( ) Bu durumda, akışkandan türbine aktarılan mekanik enerji ve toplam verim, D Emek,akışkan = m (emek, giren - emek,çıkan ) = (5000 kg/s)(0.491kJ/kg) = 2455 kW htoplam = htürbin-jen = Welekt, çıkan D Emek, akışkan 1862 kW = = 0.76 2455 kW b) Toplam verimi ve jeneratör verimini bildiğimizden, türbinin mekanik verimi: htürbin-jen = htürbin h jen ® htürbin = htürbin-jen h jeneratör 0.76 = = 0.80 0.95 c) Alınan mil gücü ise mekanik verim tanımından hesaplanabilir: Welekt, çıkan = htürbin D Emek, akışkan = (0.80)(2455kW) = 1964 kW Enerjinin sadece mekanik formlarını ve mil işi transferini içeren sistemler için, enerjinin korunumu ilkesi: Emek, giren - Emek, çıkan = D Emek, sistem + Emek, kayıp Emek, kayıp Þ sürtünme gibi tersinmezliklerden kaynaklanan mekanik enerjinin ısıl enerjiye dönüşümünü gösterir. Daimi halde çalışan bir sistem için mekanik enerji dengesi: Emek, giren - Emek, çıkan = Emek, kayıp GENEL ENERJİ DENKLEMİ Temel yasaların en önemlilerinden biri de Termodinamiğin Birinci Yasası veya Enerjinin Korunumu yasasıdır. Bu yasaya göre enerji vardan yok yoktan var edilemez, sadece biçim değiştirir. Düşen bir kaya PE-KE dönüşümü yoluyla hız kazanır Hava direnci yoksa PE + KE = sabit olmalıdır Genel Enerji Denklemi Kapalı bir sistemin enerjisi iki şekilde değişebilir; ısı transferi Q ve iş W Kapalı bir sistemin birim zamandaki enerji değişimi şu şekilde verilir: Qnet , giren Wnet , giren dEsis dt Sisteme birim zamanda geçen NET ısı: Qnet , giren Qgiren Qçıkan Birim zamandaki NET iş ise: Wnet , giren Wgiren Wçıkan Genel Enerji Denklemi RTT şu şekilde verilmişti: dBsis d bdV b Vb n dA KY dt dt KH B = E ve b=e alınırsa; dEsis d Qnet , giren Wnet , giren edV e Vb n dA KY dt dt KH İş terimi; basınç işi ile mil işinin toplamı olarak yazılabilir: Wnet , giren Wmil ,net , giren Wbasınç ,net , giren Wmil ,net , giren P V n dA A Genel Enerji Denklemi Mil işi nereden kaynaklanıyor? Piston aşağı doğru, F=PA kuvvetinin etkisiyle ds mesafe kadar itildiğinde, sistem üzerinde dWsınır=PAds. kadar iş yapılır. Her iki taraf dt ye bölünerek: d Wbasınç d Wsınır PA ds PAV piston dt Genel kontrol hacimleri için: d Wbasınç PdAVn PdA V n V ve n vektörleri zıt yönlü olduğundan skaler çarpımları negatiftir. İşin negatif çıkması, sistem üzerine yapıldığını da güvence altına alır. Genel Enerji Denklemi Böylece enerji denklemi şu şekilde elde edilir: P d Qnet , giren Wmil ,net , giren edV e e Vb n dA dt KH KY görülen P/ akış işi olup birim kütle başına akışkanı KH içerisine sürmek için yapılan işi temsil eder. Denklemde Genel Enerji Denklemi Kütle korunumu denkleminde olduğu gibi, pratikte genellikle giriş/çıkışlar üniform olarak düşünülür. Bu durumda denklem: Qnet , giren Wmil ,net , giren m V n dA P P d edV m e m e dt KH çıkan giren c AC Öte yandan e=u+ke+pe = u+V2/2+gz olduğundan P P d V2 V2 Qnet , giren Wmil ,net , giren edV m u gz m u gz dt KH 2 2 çıkan giren DAİMİ (SÜREKLİ REJİMDE) ÇALIŞAN SİSTEMLER Qnet , giren Wmil ,net , giren V2 V2 m h gz m h gz 2 2 çıkan giren Daimi akışta KH içeriğinde hiçbir değişiklik yoktur. Tek giriş ve çıkışın bulunduğu durumlarda; V22 V12 qnet , giren wmil ,net , giren h2 h1 g z2 z1 2 P1 V12 P2 V22 wmil ,net ,in gz1 gz2 u2 u1 qnet , giren 1 2 2 2 V12 P2 V22 gz1 wpompa gz2 wtürbin emek ,kayıp 1 2 2 2 P1 Birim kütle başına yazıldığında birim kJ/kg olur, güç birimi (W) ortadan kalkar Daimi akışların enerji analizi Enerji denkleminin tüm terimleri g ye bölünürse P1 V12 P2 V22 z1 hpompa z2 htürbin hK 1 g 2 g 2 g 2 g Bu durumda her bir terim eşdeğer akışkan sütunu yüksekliği cinsinden ifade edilmiş olur. Bu terimlere YÜK adı verilir. P V z Basınç Yükü Hız Yükü Po tan siyel Yük HİDROLİK YÜK H g 2g BERNOULLI DENKLEMİ Enerji denkleminden iş, ısı ve kayıp terimlerini atarsak, elde ettiğimiz denkleme Bernoulli Denklemi denir. P1 V12 P2 V22 z1 z2 sabit H 1 g 2 g 2 g 2 g Bu denklem bir akım çizgisi boyunca hareket eden bir akışkan parçacığına Newton’un İkinci yasası uygulanarak da bulunabilir (Bkz sayfa 186-187) Statik, Dinamik ve Durma Basınçları Bernoulli Denklemi, her bir terim basınç biriminde olacak şekilde de ifade edilebilir. Bu durumda terimler şu isimleri alır: P Statik Basınç V2 2 gz Hidrostatik Basınç PT Toplam Basınç Dinamik Basınç DURMA BASINCI , Pdurma Bernoulli Denklemi, her bir terim basınç biriminde olacak şekilde de ifade edilebilir. Bu durumda terimler şu isimleri alır: PİTOT TÜPÜ ile hız ölçümü Statik, Dinamik ve Durma basınçları yandaki gibi bir düzenekle ölçülebilir. Bu şekilde durma basıncının ölçülmesi, kanal veya borudaki hızın hesaplanmasına olanak verir. Bu esasa göre çalışan ölçüm aygıtlarına PİTOT TÜPÜ adı verilir. P Statik Basınç V2 2 Pdurma Dinamik Basınç V 2 Pdurma Pstatik Hidrolik Eğim Çizgisi (HEÇ) Enerji Eğim Çizgisi (EEÇ) Akışkanın mekanik enerjisini yükseklikler cinsinden çizmek çoğu zaman kolaylık sağlar. HEÇ P HEÇ z g EEÇ 2 P V EEÇ z g 2g Hidrolik Eğim Çizgisi (HEÇ) Enerji Eğim Çizgisi (EEÇ) İdeal Bernoulli akışında EEÇ yatay bir doğrudur. Ancak akış kesiti değişiyorsa HEÇ için aynı şeyi söyleyemeyiz. Gerçek viskoz akışta EEÇ akış yönünde düşme gösterir. Akışkana enerji verildiğinde EEÇ dik bir yükseliş, akışkandan enerji çekildiğinde ise dik bir düşüş sergiler. HEÇ’in akışkanla kesiştiği noktalarda etkin basınç SIFIR olur. Bu kesişim noktalarının üzerinde vakum meydana gelir.