2. Tek-Serbestlik-Dereceli

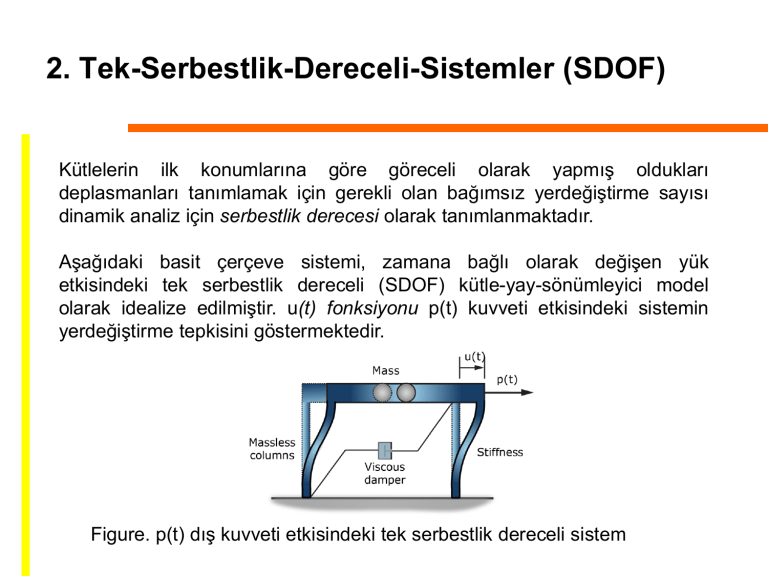
2. Tek-Serbestlik-Dereceli-Sistemler (SDOF)
Kütlelerin ilk konumlarına göre göreceli olarak yapmış oldukları
deplasmanları tanımlamak için gerekli olan bağımsız yerdeğiştirme sayısı
dinamik analiz için serbestlik derecesi olarak tanımlanmaktadır.
Aşağıdaki basit çerçeve sistemi, zamana bağlı olarak değişen yük
etkisindeki tek serbestlik dereceli (SDOF) kütle-yay-sönümleyici model
olarak idealize edilmiştir. u(t) fonksiyonu p(t) kuvveti etkisindeki sistemin
yerdeğiştirme tepkisini göstermektedir.
Figure. p(t) dış kuvveti etkisindeki tek serbestlik dereceli sistem
2. Tek-Serbestlik-Dereceli-Sistemler (SDOF)
Yapılan idealleştirme çerçevesinde, yapının tüm kütlelerinin tek bir
noktada toplandığı ve kiriş rijit olarak kalırken, tüm deformasyonun
kolonlarda oluştuğu kabul edilmektedir. Kütlesiz kolonlar, sisteme
rijitlik kazandırmaktadır. Ayrıca, lineer dinamik analize olanak
vermesi nedeniyle, sönümün viskoz sönüm olarak ele alınması
yaygın olarak tercih edilen bir yöntemdir.
2.1. Hareket Denklemi için Dinamik Denge
(D’Alambert İlkesi)
Bu prensibe göre, atalet kuvveti olarak bilinen hayali bir kuvvetin dış
kuvvetlere ilave edilmesiyle, dikkate alınan sistem dinamik denge
konumuna ulaşmış olur.
Şekil. SDOF sistem için analitik model (mekanik sistem)
Bilindiği gibi yapı sistemlerinin çözümünde, sistemin serbest cisim
diyagramı çizilir ve denge denklemi yazılır. Aslında, D’Alambert ilkesi
de aynı prensibe sahip olup, tek fark dinamik denge denkleminin
yazılmasıdır.
2.1. Hareket Denklemi için Dinamik Denge
(D’Alambert İlkesi)
Serbest Cisim Diyagramı
p(t)
: dış kuvvet
fI(t)
: atalet kuvveti
fD(t)
: sönüm kuvveti
fS(t)
: yay (rijitlik) kuvveti
• Yay k rijitliğine sahip lineer bir yay olup, rijitlik kuvveti olarak bilinen ku
kuvvetini ortaya çıkarmaktadır.
fS
1
fS(t)=ku(t)
k
u
(2.1.1)
2.1. Hareket Denklemi için Dinamik Denge
(D’Alambert İlkesi)
• Sönümleyici, viskoz türde bir sönümleyici olup,
olmaktadır.
f D (t)  cu (t) burada
u 
du
dt
cu sönüm kuvvetine neden
(velocity )
(2.1.2)
fD
1
c
cu
Bir kütlenin sıvı içindeki hareketine karşı oluşacak tepkiye benzer biçimde,
sönüm kuvvetini kütlenin hızıyla orantılı olarak kabul eden viskoz sönüm
modeli, doğrusal modele olanak sağladığı için dinamik hesaplarda en sık
kullanılan sönüm modelidir.
2.1. Hareket Denklemi için Dinamik Denge
(D’Alambert İlkesi)
• Atalet kuvveti kütle ile ivmenin çarpımına eşittir ve sistemin hareket yönüne
ters yönde etkimektedir.
d 2u
f I (t)  mü(t) burada ü  2 (accelerati on) (2.1.3)
dt
Bu durumda, hareket
edilmesinden ibarettir.
denklemi
bu
kuvvetlerin
f I (t)  f S (t)  f D (t)  p(t)
dengesinin
ifade
(2.1.4)
(2.1.1-2.1.3) denklemleri, (2.1.4) denkleminde yerine yazılırsa, tek
serbestlik dereceli sistemin hareket denklemi elde edilir.
mü  cu  ku  p(t)
(2.1.5)
2.2. Hareket Denklemi için Newton’un İkinci
Hareket Kanunu
Serbest Cisim Diyagramı
Net kuvvet (p(t)- fS(t)- fD(t)) olduğuna göre,
Newton’un ikinci hareket kanunu yazılacak
olursa,
p(t) - f S (t)  f D (t)  mü
(2.2.1)
mü  cu  ku  p(t)
(2.2.2)
2.2. Hareket Denklemi için Newton’un İkinci
Hareket Kanunu
mü  cu  ku  p(t)
Elde edilen hareket denklemi, sabit katsayılı ikinci dereceden lineer
bir diferansiyel denklemdir. Statik problemin çözümü için bilindiği
gibi cebirsel bir denklem yazılmaktadır. Ancak, dinamik yük
etkisindeki bir sistemin çözümünde söz konusu cebirsel denklem,
ikinci dereceden bir diferansiyel denkleme dönüşmektedir. İkinci
dereceden diferansiyel denklem çözümünün, statik problemin
cebirsel denkleminin çözümünden daha karmaşık olduğu bilinen bir
gerçektir.
Tek Serbestlik Dereceli Sistemin Hareket Denklemi
Tek serbestlik dereceli sistemin hareket denkleminin elde edilmesi
için aşağıdaki çerçeve sistem ele alınsın.
Sistemde kolonların eksenel rijitliği sonsuz iken, kiriş eksenel ve
eğilme rijitlikleri sonsuzdur. Kiriş tamamen rijit ve kolonlar eksenel
olarak rijit olduğundan, sisteme düşey ağırlık kuvvetlerinin etkimesi
durumunda, söz konusu kuvvetler doğrudan tabana aktarılacaktır. Bu
durumda, yapıda yerdeğiştirme oluşturacak tek yükleme durumu,
yatay yükleme durumudur. Sistemin yatay rijitliği, tamamen eğilme
etkisindeki kolonların rijitliği ile sağlanmaktadır.
Mukavemet bilgilerinden;
Şekil. Dört kolona oturan rijit platform (a) Sistem (b) Deplasman yapmış
kolona etkiyen kuvvetler (c) Kütleye etkiyen yatay kuvvetler
Tek Serbestlik Dereceli Sistemin Hareket Denklemi
Kütleye ait serbest cisim diyagramı çizilir ve herhangi bir t anında rijit
kütleye etkiyen kuvvetler gösterilirse,
Net kuvvet (p(t)- fS(t)- fD(t)) olduğuna göre, Newton’un ikinci hareket
kanunu yazılırsa,
p(t) -
12 EI
12 EI
u

u  f D (t)  mü
L3
L3
(2.2.4)
Sönüm kuvveti de f D (t)  cu (t) dahil edilirse
mü  cu 
24 EI
u  p(t)
3
L
(2.2.5)
Tek Serbestlik Dereceli Sistemin Hareket Denklemi
k
24EI
L3
olduğuna göre, hareket denklemi
mü  cu  ku  p(t)
(2.2.6)
Yay Rijitlikleri
Kolonlarda gösterilen k1 ve k2 rijitlikleri, her bir kolonun u ile
gösterilen serbestlik yönünde harekete karşı direncini
temsil etmektedir. Eğer her iki kolonun da aynı anda aynı
yatay ötelenmeyi yapacağı varsayılırsa, sistemin toplam
rijitliği k=k1+k2 olur. Bir yapı içinde bulunabilecek değişik
elemanları yansıtmak için, gerekirse modelde birden fazla
yay da kullanılabilir. Gerçek yapılardaki kiriş gibi
elemanların rijitliği de kullanılan malzemeye bağlı olarak
statik hesap yöntemleri ile hesaplanır. Birden fazla yay
veya yapı elemanının bulunduğu daha karmaşık
sistemlerde modelin rijitliğini tek bir sabitle belirtmek için,
eşdeğer yay sabiti olarak bilinen ke oluşturulabilir (Tablo
2.2.1-2.2.2).
Yay Rijitlikleri
Sistem (Model)
Eşdeğer Yay Sabiti
ke  k
ke 
1
n
k
i 1
i
n
ke   ki
i 1
Tablo 2.2.1 Çeşitli yay sistemleri için eşdeğer yay sabitleri
Eşdeğer Yay Sabitleri
Sistem (Model)
Eşdeğer Yay Sabiti
PL3

48 EI
 1 P  k 
48 EI
k  3  ke
L
ke 
3EI
L3
Tablo. Yapı modellerinde kullanılan bazı doğrusal-elastik elemanların
eşdeğer yay sabitleri
2.3. Hareket Denklemi: Ağırlık Kuvvetleri
2.3. Hareket Denklemi: Ağırlık Kuvvetleri
Serbestlik derecesi doğrultusunda ağırlık kuvvetleri elde etmek için, yaykütle sisteminin 90 döndürülmesiyle elde edilen yukarıdaki sistem ele
alınsın. Rijit kütlenin ağırlığı W, (2.2.6) denkleminin sağ tarafına eklenirse;
f I (t)  f S (t)  f D (t)  p(t)  W
mü t (t )  cu t (t )  kut (t )  p(t)  W
(2.3.1)
(2.3.2)
Toplam yerdeğiştirme ut, W ağırlığından ortaya çıkan ust statik
yerdeğiştirmesi ile, dinamik kuvvetin neden olduğu u yerdeğiştirmesinin
toplamına eşit olması durumunda,
u t (t )  u(t)  u st
u t (t )  u (t)
ut (t )  u(t)
(2.3.3)
2.3. Hareket Denklemi: Ağırlık Kuvvetleri
Elastik kuvvet,
f S (t)  kut (t)  kust  ku(t )
(2.3.4)
(2.3.3) ve (2.3.4) denklemleri , (2.3.2) denkleminde yerine yazılırsa,
mü(t )  cu (t )  kust  ku(t )  p(t)  W (2.3.5)
kust=W, olduğuna göre
mü(t )  cu(t )  ku(t )  p(t)
(2.3.6)
Statik denge konumunun esas alınarak yazılması durumunda, lineer
elastik bir sistemin hareket denklemi, ağırlık kuvvetlerinden
etkilenmeyecektir.
Örnek: Konsol bir kiriş ucundaki yaya asılı olan w ağırlığının hareket
denklemini elde ediniz. Yayın ve kirişin kütlesini ihmal ediniz. E=204000
N/mm2.
Fig. (a) Sistem; (b) deforme olmamış, deforme olmuş, ve statik denge
konumları; (c) serbest-cisim diyagramı; (d) yay ve kiriş kuvvetleri
2.4. Hareket Denklemi: Deprem Etkisi
Şekilde görüldüğü gibi yapı sistemine doğrudan etkiyen bir dış
kuvvet bulunmamaktadır. Yapıdaki yerdeğiştirme ve gerilmeler,
deprem
nedeniyle
mesnet
noktalarının
hareketinden
kaynaklanmaktadır. Burada sabit referans eksene göre ug(t) rölatif
yer hareketi ile tanımlanan deprem hareketinin sadece yatay
bileşeni dikkate alınacaktır.
Mesnet hareketinin tek serbestlik dereceli sistemin dengesine etkisi: (a)
sistemin hareketi; (b) denge kuvvetleri
2.4. Hareket Denklemi: Deprem Etkisi
Burada, kirişin rijit olduğu ve hareket eden tüm kütleyi içerdiği
kabul edilirken, düşey kolonlar kütlesiz ve eksenel olarak rijit kabul
edilmektedir. Her bir kolonun eğilme rijitliği k/2 olarak
tanımlanırken, kütlenin tek bir serbestlik derecesi ,u(t), söz konusu
olmaktadır. Bunun yanında, c sönümleyicisi de serbestlik derecesi
doğrultusunda harekete ters yönde ve hızla orantılı olan bir direnç
oluşturmaktadır.
Rijit bir temel için sistemin tabanındaki yerdeğiştirme ug(t) olarak
tanımlanırken, söz konusu yerdeğiştirme tabliye hizasında
toplanan kütlenin tabana göre rölatif yerdeğiştirme u(t)
yapmasında neden olmaktadır.
2.4. Hareket Denklemi: Deprem Etkisi
Tabliye hizasında toplam yerdeğiştirme,
u t (t )  u g (t )  u(t )
(2.4.1)
Kütlenin serbest cisim diyagramı dikkate alınırsa,
f I (t)  f S (t)  f D (t)  0
(2.4.2)
Elastik ve sönüm kuvvetleri (2.1.1) ve (2.1.2) denklemleri ile verilirken,
atalet kuvveti, toplam ivmeye bağlı olarak aşağıdaki gibi
tanımlanmaktadır.
f I (t)  mü t (t)
(2.4.3)
Bu ifadeler, (2.4.2) denkleminde yerine yazılırsa,
2.4. Hareket Denklemi: Deprem Etkisi
mü t (t )  cu (t )  ku(t )  0
ü t (t )  ü(t )  üg (t ) (2.4.5)
(2.4.4)
olduğuna göre, (2.4.5) ifadesi (2.4.4) denkleminde
yerine yazılırsa,
mü(t )  müg (t )  cu (t )  ku(t )  0
(2.4.6)
üg(t) eşitliğin sağ tarafına atılarak, deprem hareketi etkisindeki tek
serbestlik dereceli bir sistemin hareket denklemi elde edilir.
mü(t )  cu (t )  ku(t )  peff (t )
peff (t )  müg (t )
(2.4.7)
(2.4.8)
2.4. Hareket Denklemi: Deprem Etkisi
peff(t), deprem hareketinin yapı üzerindeki etkisine eşdeğer olan, etkin
sismik kuvveti ifade etmektedir. Başka bir ifade ile, üg(t) yer hareketi
etkisindeki yapı sisteminin u(t) yerdeğiştirmesi , zemine ankastre ve kütle
ile yer hareket ivmesinin çarpımına eşit ve ters yönde uygulanan dış
kuvvet etkisindeki aynı yapı sisteminin yerdeğiştirmesi ile aynı olacaktır.