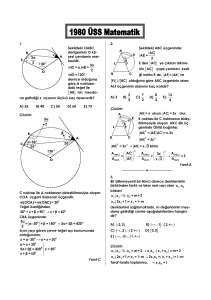
1.
Aynı bir düzleme paralel olmayan(aykırı) üç
doğru veriliyor. Bu üç doğruyu kesen kaç doğru
vardır?
A) ∞
B) 3
C) 2
D) 1
E) 0
3.
y = 3x 2 - 6x + 3 parabolü veriliyor. Koordinat eksenlerinin başlangıç noktası bu parabolün minimum noktasına kaydırıldığı taktirde, aşağıdakilerden hangisi parabolün yeni denklemini verir?
Çözüm:
Aynı bir düzleme paralel olmayan(aykırı) üç
doğruyu kesen sonsuz doğru vardır.
Yanıt:A
A) y=x
2.
Tepe noktasının koordinatları cinsinden parabol
denklemi;
2
y = a ( x - r ) + k biçiminde olduğuna göre a=3
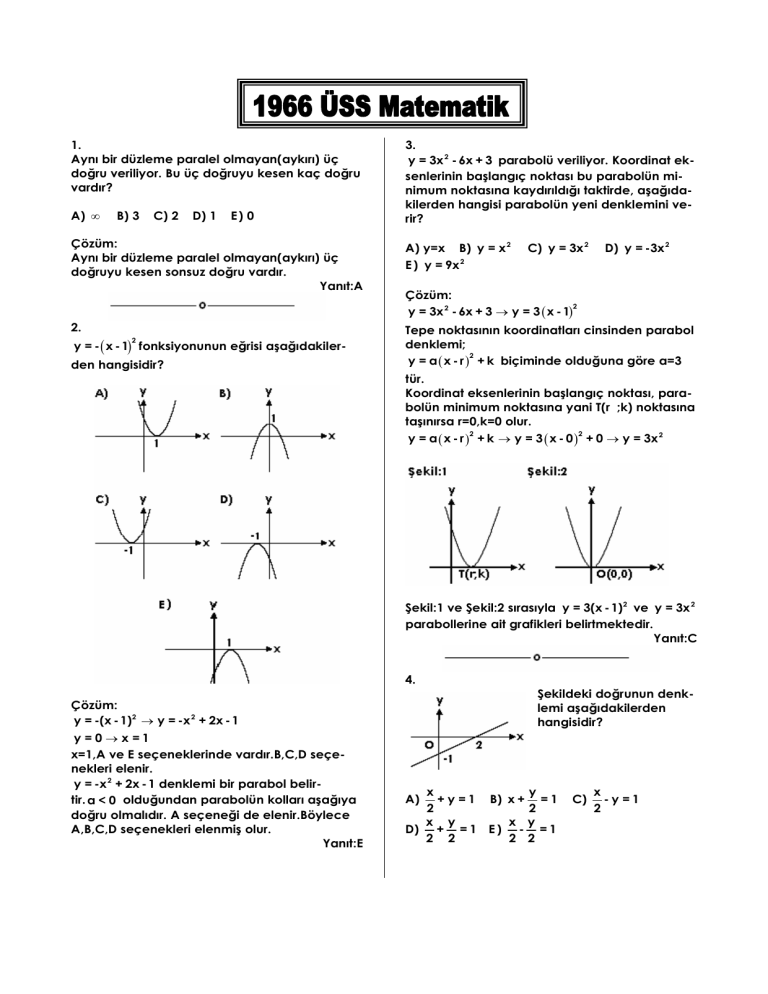
y = - ( x - 1) fonksiyonunun eğrisi aşağıdakiler2
den hangisidir?
B) y = x 2
E ) y = 9x
C) y = 3x 2
D) y = -3x 2
2
Çözüm:
2
y = 3x 2 - 6x + 3 → y = 3 ( x - 1)
tür.
Koordinat eksenlerinin başlangıç noktası, parabolün minimum noktasına yani T(r ;k) noktasına
taşınırsa r=0,k=0 olur.
y = a ( x - r ) + k → y = 3 ( x - 0 ) + 0 → y = 3x 2
2
2
Şekil:1 ve Şekil:2 sırasıyla y = 3(x - 1)2 ve y = 3x 2
parabollerine ait grafikleri belirtmektedir.
Yanıt:C
4.
Şekildeki doğrunun denklemi aşağıdakilerden
hangisidir?
Çözüm:
y = -(x -1)2 → y = -x 2 + 2x - 1
y =0 → x =1
x=1,A ve E seçeneklerinde vardır.B,C,D seçenekleri elenir.
y = -x 2 + 2x - 1 denklemi bir parabol belirtir. a < 0 olduğundan parabolün kolları aşağıya
doğru olmalıdır. A seçeneği de elenir.Böylece
A,B,C,D seçenekleri elenmiş olur.
Yanıt:E
x
y
+ y = 1 B) x + = 1
2
2
x y
x y
D) + = 1 E ) - = 1
2 2
2 2
A)
C)
x
-y =1
2
1966 ÜSS MATEMATĐK SORU VE ÇÖZÜMLERĐ
Çözüm:
7.
y=mx+m-1 doğrularının hepsinde ortak olan
nokta aşağıdakilerden hangisidir?
Doğru A(2;0) ve B(0;-1)
noktalarından geçmektedir. Đki noktadan geçen
doğru denklemi;
x - xA
y - yA
=
x A - x B y A - yB
A) (0;1)
E ) (1;0)
B) (-1;-1)
C) (-2;2)
D) (1,-2)
Çözüm:
Ortak nokta A olsun.
m=2 için y=2x+1
m=3 için y=3x+2
y = 2x + 1
x = -1, y = -1 → A(-1;-1)
y = 3x + 2
x-2
y-0
x
=
→ -y =1
2 - 0 0 - (-1)
2
Yanıt:C
5.
Yanıt:B
ABCD dikdörtgeninde
OA = 2, OC = 5, OD = 3
dür. OB nin uzunluğu
8.
Đki çemberin yarıçapları sırasıyla 2 cm ve 4 cm
dir. Bu iki çemberin birbirini dik kesmesi için
merkezleri arasındaki uzaklık aşağıdakilerden
hangisidir?
nedir?
A) 10
B) 20
C) 5
D) 10
E ) 15
2
B) 4 5
A) 5 5
Çözüm:
2
2
OA + OC = OD + OB
C) 5 3
D) 5 2
E) 2 5
2
Çözüm:
2
2 2 + 52 = 3 2 + OB → OB = 20
KHL dik üçgeninde;
2
2
KL = KH + LH
Yanıt:B
2
= 4 2 + 22 = 20
KL = 2 5 cm
6.
x 2 + y 2 = 25 dairesinin A(5;0) noktasındaki teğetinin denklemi aşağıdakilerden hangisidir?
Yanıt:E
A) x-y=5
E) x-y=0
B) x+y=5
C) y-5=0
D) x-5=0
9.
y = x 3 - x eğrisi ile apsisler ekseninin sınırladığı
alanlardan üst taraftakinin değeri nedir?
Çözüm:
Çember üzerinde bulunan
K(p;q) noktasından çembere çizilen teğetin denklemi
px + qy = r 2
biçimindedir.
O halde
x 2 + y 2 = 25
çemberine üzerindeki A(5;0) çizilen teğetin denklemi;
5x + 0.y = 25 → x - 5 = 0 olur.
Yanıt:D
A)
3
2
B)
5
4
C)
3
4
D)
1
2
E)
1
4
Çözüm:
y = 0 için
x 1 = -1, x 2 = 0
x 3 = 1 dir.
Apsisler ekseninin sınırladığı alanlardan üst taraftakinin değeri şekildeki taralı
alandır. Taralı alan S olsun.
2
1966 ÜSS MATEMATĐK SORU VE ÇÖZÜMLERĐ
0
S=∫
-1
(
0
Çözüm:
Doğru A(2;2) ve O(0;0) noktalarından geçmektedir. Đki noktadan
geçen doğru denklemini veren bağıntıdan faydalanarak;
x - xA
y - yO
=
x A - xB yO - yO
x4 x2
x - x dx =
-
4 2 -1
3
)
4
2
0 4 0 2 (-1) (-1)
1
→ S = br 2
= - -
2
4
4 2 4
Yanıt:E
x-2 y-2
=
→y=x
2- 0 2-0
Yanıt:B
10.
log20-log(x-1)=1 denklemine uyan x’in değeri
aşağıdakilerden hangisidir?
A) 3
B)
3
2
C) -
3
2
D) -2
13.
E ) -3
x 5 -1
değeri aşağıdakilerden hangisine eşitx →1 x -1
tir?
lim
Çözüm:
log20 -log(x -1) = 1 → log
20
20
= 1→
= 101
x -1
x -1
A) 5
20
= 10 → x = 3
x -1
C) 45
D) 60
E ) 90
m2 -m1
1+ m1m2
3 -0
= 3
β = 60 0
14.
x+y=4 ve x-z=1 olduğuna göre; x 2 + xy - xz - yz
ifadesinin değeri aşağıdakilerden hangisidir?
Yanıt:D
A) 2
12.
A(2;2) noktasını başlangıç noktasına birleştiren
doğrunun denklemi aşağıdakilerden hangisidir?
A) y =
x
2
B) y=x
C) y=2x D) y=-x
)
2.yol:
x 5 -1 0
lim
→ belirsizliği vardır. L’Hospital kuralıx →1 x -1
0
nın(Pay ve paydanın türevi) uygulanmasıyla;
x 5 -1
5x 4 - 0 5.14
lim
= lim
=
=5
x →1 x -1
x →1 1- 0
1
Yanıt:A
y = 3x + 1 → m2 = 3
1+ 0. 3
(
= 14 + 13 + 12 + 1+ 1= 5
Doğruların eğimleri;
y =1
→ m1 = 0
tgβ =
E) 1
(x -1) x 4 + x 3 + x 2 + x + 1
x 5 -1
= lim
x →1 x -1
x →1
(x -1)
lim
Çözüm:
tgβ =
D) 2
1.yol:
x 5 -1 0
lim
→ belirsizliği vardır.
x →1 x -1
0
11.
y = 3x + 1 ile y=1 doğruları kaç derecelik açı
altında kesişirler?
B) 30
C)3
Çözüm:
Yanıt:A
A) 0
B) 4
E) y =
B) 3
C) 4
D) 5 E ) 6
Çözüm:
Đki ifadenin taraf tarafa çarpılmasıyla;
(x + y)(x - z) = 4.1 → x 2 + xy - xz - yz = 4
x
3
Yanıt:C
3
1966 ÜSS MATEMATĐK SORU VE ÇÖZÜMLERĐ
15.
2x 2 - 4x + m- 3 = 0 denkleminde x 12 + x 22 = 4 ol-
Çözüm:
( x - x1 )( x - x 2 )( x - x 3 ) = 0
ması için m aşağıdakilerden hangisidir?
[ x - (-2)][ x -(-1)] (x - 0) = 0
A) 0
x 3 + 3x 2 + 2x = 0
B) 1
C) 2
D) 3 E ) 4
Yanıt:A
Çözüm:
2x 2 - 4x + m- 3 = 0
18.
(-4 ) - 2.2(m- 3)
b2 - 2ac
x +x =
→4=
a2
22
m=3
2
2
1
a
fonksiyonunun gösterdiği eğrinin
2x -1
B(1;1) noktasından geçmesi için a ne olmalıdır?
2
2
y=
Yanıt:D
A) ∞
C) 1
D) -1
E) 0
Çözüm:
16.
x 2 + y 2 - 4x + 2y - 3 = 0 çemberine Üzerindeki
(4;1) noktasından çizilen teğetin denklemi aşağıdakilerden hangisidir?
A) 2x+y-5=0
D) x+y-6=0
B) 2
B(1;1) noktası eğri üzerinde olduğundan koordinatları eğri denklemini
sağlar;
a
a
y=
→ 1=
2x -1
2.1-1
a=1
B) x-y-3=0 C) x-2y-5=0
E ) x+y-5=0
Çözüm:
Yanıt:C
Denklemi ( x -a ) + ( y -b ) = r 2
2
2
olan çembere üzerindeki
K(p;q) noktasından çembere
çizilen teğetin denklemi;
(x -p)(p- a) + (y - q)(q-b) = 0
19.
Şekilde görülen üçgende
a=8 cm,b=5 cm,c=7 cm olduğuna göre DC kaç cm
x 2 + y 2 - 4x + 2y - 3 = 0 çember
denkleminde;
D
-4
a =- =- → a = 2
2
2
E
2
b = - = - → b = -1
2
2
(x -p)(p- a) + (y - q)(q-b) = 0
dir?
A) 1
C) 3
D) 4
E) 5
Çözüm:
(x - 4)(4 - 2) + (y -1) [1-(-1)] = 0
Problem verilerinden
faydalanarak yandaki
şekil elde edilebilir.
Teğet özelliğinden;
AE = AF , FB = BD ,
Yanıt:E
17.
Kökleri -2,-1 ve 0 olan üçüncü dereceden
denklem aşağıdakilerden hangidir?
A) x 3 + 3x 2 + 2x = 0
C) x 3 + 3x 2 - 2x = 0
E ) x 3 - 3x 2 + 1= 0
B) 2
CD = CE
B) x 3 - 3x 2 + 2x = 0
D) x 3 + 3x 2 + 2x + 1= 0
AB = (8- x) + (5- x)
7 = (8 - x) + (5- x) → x = 3 cm → DC = 3 cm
Yanıt:C
4
1966 ÜSS MATEMATĐK SORU VE ÇÖZÜMLERĐ
20.
a = 30 0 olan bir üçgende a kenarı 5 cm dir.
Çevrel çemberin çapı aşağıdakilerden hangisine eşittir?
A) 2,5
5 3
B)
2
5 2
C)
2
D) 5
E seçeneği:
x
1
1
y=
=
=
x + 1 1+ 1 2
y=0 olmadığından C,D,E seçenekleri elenir.
Doğru yanıtı bulmak için asimptotlara bakmakta fayda vardır.
E ) 10
A seçeneği:
Yatay asimptot:
x -1
y = lim
→ y =1
x →∞ x + 1
Çözüm:
R,çevrel çemberin çapını göstermek üzere sinüs
teoremi;
a
5
5
=R →
= R → = R → R = 10 cm
1
sinA
sin300
2
Yanıt:E
Düşey asimptot:
x + 1= 0 → x = -1
B seçeneği:
Yatay asimptot:
x -1
y = lim
→ y =1
x →∞ x
Düşey asimptot:
x=0
21.
Yatay asimptot hem A seçeneğinde hem de B
seçeneğinde 1 dir. Yatay asimptottan faydalanarak sonuca ulaşılamaz. Şekle göre düşey asimptot y-ekseni yani x=0 doğrusudur. Bu durumda A seçeneği de elenir.Böylece A,C,D,E
seçenekleri elenmiş olur.
Yanıt:B
Aşağıdaki fonksiyonlardan hangisi
şekildeki eğrinin
karşılığıdır?
x -1
x +1
x
D) y =
x -1
A) y =
22.
Bir ABC üçgeni için aşağıdakilerden hangisi
yanlıştır?
x -1
x +1
C) y =
x
x -1
x
E) y =
x +1
B) y =
A) sin2 A + cos2 A = 1
C) 2RsinA=a
E ) sin(A+B)=sinC
Çözüm:
Fonksiyona ait grafiğin x-eksenini
kestiği nokta olan
A noktasında
x=1,y=0 dır. A(1;0)
noktası grafik üzerinde olduğundan
Grafiğe ait denklemi sağlamalıdır.
A seçeneği:
x -1 1-1
y=
=
=0
x + 1 1+ 1
B seçeneği:
x -1 1-1
y=
=
=0
x
1
C seçeneği:
x + 1 1+ 1
y=
=
=∞
x -1 1-1
D seçeneği:
x
1
y=
=
=∞
x -1 1-1
B) a2 = b2 + c2 - 2bccosA
D) asinA=bsinB
Çözüm:
Sinüs teoremi;
a
b
=
→ asinB = bsinA
sinA sinB
Yanıt:D
23.
Taban yarıçapı 1 ve 2,yüksekliği 3 olan kesik
koninin hacmi nedir?
A) 5 π
B) 6 π
C) 7 π
D) 8 π
E ) 9π
Çözüm:
Kesik koninin hacmini veren bağıntıdan faydalanarak;
5
1966 ÜSS MATEMATĐK SORU VE ÇÖZÜMLERĐ
1
1
πh r12 + r1r2 + r22 = π.3 22 + 2.1+ 12
3
3
V = 7 π br 2
(
V=
)
(
(
)
D) ± 5; 0
)
(
E ) − 5; 5
Çözüm:
4x 2 + 9y 2 = 36
Yanıt:C
x2 y2
+
=1
9
4
a2 = 9,b2 = 4
24.
1
+ 2x -1 fonksiyonu aşağıdakilerden
x2
hangisinin türevidir?
a2 = b 2 + c 2
y' = -
9 = 4 + c2 → c = ± 5
O halde elipsin odaklarının koordinatları;
(±
3
1
+ x 2 - x B) y = + x 2 - x
x3
x
1
3
C) y = - + x 2 - x
D) y = 3 + x 2 + x -1
x
x
1
2
E ) y = + x + x -1
x
A) y = -
5; 0
)
Yanıt:D
27.
Şekilde A = 100 0 olduğuna göre, DOB açısı
kaç derecedir?
Çözüm:
1
y = ∫ - 2 + 2x -1dx → y = ∫ -x -2 + 2x -1 dx
x
(
=-
)
A) 110
C) 130
E ) 160
x -2+1
x 1+1 x 0+1
1
+ 2.
→ y = + x2 - x
-2 + 1
1+ 1 0 + 1
x
Yanıt:B
B) -2
C) 2
D) 3
ABCD dörtgeni kirişler
dörtgeni olduğundan
karşılıklı açılar toplamı
180 0 dir.
E) 4
m(DAB) + m(DCB) = 180 0
Çözüm:
100 0 + m(DCB) = 180 0
2
x + x(4- 2p) + 4 = 0
x - y + 2 = 0
Teğet şartının sağlanabilmesi için
diskriminant “0” olmalıdır.
b2 - 4ac = ∆
y 2 = 2px
( 4 - 2p )
2
B) 120
D) 140
Çözüm:
25.
x-y+2=0 doğrusunun y 2 = 2px parabolüne teğet
olması için p nin değeri ne olmalıdır?
A) -4
)
m(DCB) = 80 0
“Aynı yayı gören çevre
açı merkez açının yarısına eşittir” hükmünden
hareketle;
1
1
m(DCB) = m(DOB) → 80 0 = m(DOB)
2
2
- 4.1.4 = 0 → p = 4
m(DOB) = 160 0
Yanıt:E
Yanıt:E
26.
4x 2 + 9y 2 = 36 elipsin odaklarının koordinatları
aşağıdakilerden hangisidir?
(
A) 0; ± 5
)
(
B) 0; ± 10
)
(
C) ± 10; 0
28.
Bir eşkenar üçgenin alanı 400 3 cm2 olduğuna
göre, bir kenarının uzunluğu kaç cm dir?
)
A) 40 3
6
B) 40
C) 30 3
D) 20 3
E ) 20
1966 ÜSS MATEMATĐK SORU VE ÇÖZÜMLERĐ
Çözüm:
Kenar cinsinden eşkenar üçgen alanını veren
bağıntıdan faydalanarak;
a2 3
a2 3
A=
→ 400 3 =
→ a = 40 cm
4
4
Yanıt:B
31.
Đki düzlem 60 0 lik açı altında kesişmektedir. Biri
üzerinde 4 cm kenarlı kare çizilirse,bu karenin
diğer düzlem üzerindeki izdüşümünün alanı nedir?
A) 16
29.
sin2x=m eşitliğinde m’nin değeri aşağıdakilerden hangisinde bulunmaktadır?
A) -2 ≤ m ≤ 2
D) -1 ≤ m ≤ 1
B) -2 ≤ m ≤ 0
E) 0 ≤ m ≤ 1
C) -1 ≤ m ≤ 0
Yanıt:D
30.
Kenarları a ve b olan dikdörtgenin a kenarı etrafında dönmesinden meydana gelen silindir ile
b kenarı etrafında dönmesinden meydana gelen silindirin hacimleri arasındaki oran nedir?
1
π
B) 1
C)
b
a
D)
b2
a2
E)
C) 4
D) 16 2
E) 8 3
Çözüm:
Karesinin alanı A , izdüşümünün alanı A’ olsun.
1
A' = Acos60 0 = 4 2 . → A' = 8 cm2
2
Yanıt:B
Çözüm:
sin2x=m eşitliğinde -1 ≤ m ≤ 1 olmalıdır.
A)
B) 8
b3
a3
Çözüm:
Şekil:1 de yarıçap b,yükseklik a dır.
V1 = πb2 a
Şekil:2 de yarıçap a,yükseklik b dir.
V2 = πa2b
V1 πb2 a
V b
=
→ 1=
V2 πa2b
V2 a
Yanıt:C
7