1.1 Yapı Dinamiğine Giriş
• Yapı Dinamiği, dinamik yükler etkisindeki yapı
sistemlerinin dinamik analizini konu almaktadır.
Dinamik yük, genliği, doğrultusu ve etkime noktası
zamana bağlı olarak değişen yüklemedir.
P(t)
t
Analiz sonucu belirlenen, zamana bağlı yapısal tepki
değerleri de dinamik tepkiyi teşkil etmektedir.
1.1 Yapı Dinamiğine Giriş
• Yapı dinamiği problemi, statik problemden iki açıdan
önemli farklılıklar göstermektedir:
Etkiyen kuvvetin zamana bağlı olarak değişmesi
İvmenin etkisi
Klasik statik yöntemde: ku=P
Zamana bağlı değişim için aşağıdaki eşitlik kullanılarak u(t)
belirlenebilir mi?
ku(t)=P(t)
1.1 Yapı Dinamiğine Giriş
Zamana bağlı tepki değerleri yerine, tasarımcılar genellikle
maksimum tepki değerlerini bilmek isterler (umax).
Ancak, problemin dinamik karakterde olması durumunda
ku(t)=P(t) eşitliğini kullanmak doğru olmaz.
u(t) yerdeğiştirmesi için ku(t)=P(t) eşitliği kullanılacak
olursa, basit bir cebrik denklem ortaya çıkacaktır. Hatta,
doğrudam maksimum yerdeğiştirme değeri dahi bu
denklem ile kolaylıkla belirlenebilir. umax için yukarıdaki
denklem yazılacak olursa:
kumax=Pmax
1.1 Yapı Dinamiğine Giriş
kumax=Pmax
Bu durumda yapılması gereken, yüklemenin maksimum
değerini belirleyip, yukarıdaki statik denklemde yerine
yazmak ve umax için çözümlemektir.
• Ancak, dinamik problem statik problemden farklı bir
karakterdedir. Newton’un ikinci kanununa göre, “Bir yapıya
etkiyen net kuvvet, yapının ivmesi ile orantılıdır.”
d
du
d 2u
p(t ) (m ) m 2
dt
dt
dt
1.1 Yapı Dinamiğine Giriş
Bir başka ifade ile, bir cisme etki eden net kuvvetin,
meydana getirdiği ivmeye oranı sabit olup, kütleye eşittir.
Kütlenin ivmeyle çarpımına eşit olan net kuvvet atalet
kuvveti olarak tanımlanıp, dinamik denge denkleminin
statik denge denkleminden olan farklılığını yansıtmaktadır.
Atalet kuvveti, sisteme etki eden net kuvvete ters yönde
ortaya çıkmaktadır.
d 2u
p(t ) m 2
dt
Net Kuvvet = Atalet Kuvveti
1.1 Yapı Dinamiğine Giriş
Şekil (a)’da statik yük etkisindeki konsol bir kiriş görülmektedir. Kirişte
oluşacak deformasyon ve iç kuvvetler, doğrudan statik yüke (P)
bağlıdır. Diğer taraftan Şekil (b)’de aynı konsol kiriş zamanla değişen
bir yük (P(t)) etkisindedir. Şekilde görüleceği gibi, kirişin ivmesi yayılı
atalet kuvvetinin ortaya çıkmasına neden olmuştur. Atalet kuvvetinin
yapıdaki deformasyon ve iç kuvvetlere önemli bir katkısının olması
durumunda, problemin dinamik olarak ele alınması gerekmektedir.
(a) Statik Yük ve (b) Dinamik Yük, etkisindeki konsol kiriş
1.1 Yapı Dinamiğine Giriş
Statik durumda, yüklemenin sonsuz yavaş bir şekilde
gerçekleştiği kabul edilmektedir. Dolayısıyla, ortaya çıkan
ivme çok küçük olduğundan ihmal edilmektedir. Ancak,
yükleme yeterince hızlı bir şekilde yapılırsa, atalet kuvveti
diğer kuvvetlerle karşılaştırılabilecek boyutlarda olmakta ve
dolayısıyla
denge
denkleminde dikkate alınması
gerekmektedir. Bu bakımdan, ivmeden dolayı ortaya
çıkacak atalet kuvveti dinamik durumda dikkate alınmalıdır.
1.2 Yapı Bileşenlerinin ve Sistemlerinin Modellenmesi
Hesaplama aşamasında, gerçek sistemle eşdeğer olacak,
ancak aynı zamanda da matematik olarak daha kolay analiz
edilebilecek basitleştirilmiş bir model oluşturulmalıdır. Bu şekilde
elde edilecek, yapı sisteminin basitleştirilmiş modeli “analitik
model” olarak tanımlanmaktadır.
Analitik model için iki temel modellemeden bahsedilebilir:
• Sürekli Model (m(x), EI(x), C(x))
• Ayrık-Parametreli (Toplu Kütleli) Model (Mi , Ki , Ci)
Yapı sistemlerinin dinamik karakteristikleri, rijitlik, kütle ve
sönüm ile tanımlanmaktadır.
1.2 Yapı Bileşenlerinin ve Sistemlerinin Modellenmesi
Şekil. Konsol kirişe ait analitik
modeller:
(a) Yayılı-kütleli konsol kiriş, sürekli
model
(b) Tek serbestlik dereceli model,
ayrık-parametreli model
(c) Üç serbestlik dereceli model,
daha incelikli ayrık-parametreli
model
1.2 Yapı Bileşenlerinin ve Sistemlerinin Modellenmesi
Atalet kuvvetlerinin etkisini yansıtabilmek için dikkate alınması
gereken yerdeğiştirme parametre sayısı, serbestlik derecesi
(degrees of freedom, DOF) olarak tanımlanmaktadır. Bu
bakımdan, sürekli model sonsuz serbestlik derecesine
sahiptir. Ancak, Şekil b ve c, sonlu sayıda serbestlik dereceli
sistemleri içermektedir. Şekilde gösterilen ayrık-parametreli
modeller, sistemin kütlesi az sayıdaki noktasal kütle ile
gösterildiğinden, toplu kütleli sistem olarak tanımlanmaktadır.
1.2 Yapı Bileşenlerinin ve Sistemlerinin Modellenmesi
Ayrık ve sürekli sistemler:
• Tek serbestlik dereceli sistem (SDOF) system : n=1
• Çok serbestlik dereceli sistem (MDOF) system:1<n<
• Sürekli sistem
: n=
1.2 Yapı Bileşenlerinin ve Sistemlerinin Modellenmesi
Analitik modelleme için diğer bir örnek olarak, Şekilde gösterilen ayaklı
su deposu ele alınmıştır. Tepe noktasından uygulanacak yatay bir
kuvvet veya depremden kaynaklanacak yatay bir kuvvet için, bu
sistemin titreşim durumunun belirlenmesi hedeflenmiştir. Su tankının
dolu olması durumunda kullanılabilecek analitik model Şekilde ayrıca
gösterilmiştir. Dolu bir depoda suyun çalkalanma etkisi ortaya
çıkmayacağından, kütle kule tepesinde toplanırken (m), göreceli olarak
narin kuleler kütlesiz olarak modellenmiştir. Su tankını destekleyen
konsol kule yapıya yatay rijitlik (k) kazandırmaktadır.
1.2 Yapı Bileşenlerinin ve Sistemlerinin Modellenmesi
1.2 Yapı Bileşenlerinin ve Sistemlerinin Modellenmesi
Yapı sistemine ait analitik model oluşturulduktan sonra, Newton
Kanunları ve gerilme-şekildeğiştirme bağıntıları gibi fiziki kurallar
uygulanarak, analitik modeli matematik bir dil ile tanımlayan
diferansiyel denklemler elde edilir. Sürekli model, kısmi türevli
diferansiyel denklemlerin ortaya çıkmasına neden olurken, ayrıkparametreli model adi diferansiyel denklemler ortaya çıkarmaktadır.
Böylece elde edilen diferansiyel denklem takımı yapı sistemine ait
matematik model olarak tanımlanmaktadır. Kısaca, analitik model
üzerinde yazılan hareket denklemi matematik model olarak ifade
edilmektedir.
Matematik model formüle edildikten sonra dinamik analizdeki bir
sonraki adım, dinamik tepkilerin belirlenmesi için diferansiyel
denklemlerin çözümünü içermektedir.
1.2 Yapı Bileşenlerinin ve Sistemlerinin Modellenmesi
Dinamik çözümleme üş genel aşamadan oluşmaktadır:
• analitik modelin belirlenmesi
• analitik modele karşılık gelen matematik modelin belirlenmesi
• dinamik tepki için diferansiyel denklem çözümü
Yapı Dinamiği dersi kapsamında, yapı sistemlerinin dinamik
incelenmesi aşamasında, yukarıda belirtilen ikinci ve üçüncü
aşamalar üzerinde durulacaktır.
1.2 Yapı Bileşenlerinin ve Sistemlerinin Modellenmesi
Sürekli Model
Ayrık-Parametreli Model
Sürekli sistem (sonsuz-DOF sistem)
Kısmi türevli diferansiyel denklemler
Sürekli parametreler, EI(x), m(x)
Gerçekçi
Analizi zor
Toplu kütleli sistem
Adi diferansiyel denklemler
Toplu parametreler, Mi
İdealize edilmiş
Analizi kolay
Yaklaşık
u
u
(
EI
(
x
)
)
m
(
x
)
p( x, t )
x 2
x 2
t 2
2
2
2
P.D.E.
d 2u
m 2 ku p(t )
dt
O.D.E.
1.3 Kütle-Yay-Sönümleyici Sistemi
Karmaşık sistemleri incelemeden önce, en basit titreşim hareketini
yapan, en basit yapı sistem modelini ele alalım.
Kütle (m): Yapının kütlesini ve atalet özelliklerini yansıtmaktadır.
Yay (k): Yapının elastik kuvvetini ve potansiyel enerji kapasitesini
göstermektedir.
Sönüm(c): Yapının sürtünme özelliklerini ve enerji kaybını temsil
etmektedir.
Kuvvet (p(t)): Yapı sistemine etki eden dış kuvveti göstermektedir.
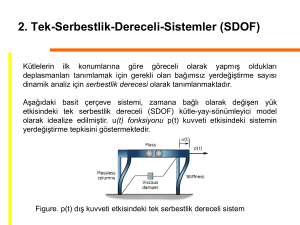
2. Tek-Serbestlik-Dereceli-Sistemler (SDOF)
Kütlelerin ilk konumlarına göre göreceli olarak yapmış oldukları
deplasmanları tanımlamak için gerekli olan bağımsız yerdeğiştirme sayısı
dinamik analiz için serbestlik derecesi olarak tanımlanmaktadır.
Aşağıdaki basit çerçeve sistemi, zamana bağlı olarak değişen yük
etkisindeki tek serbestlik dereceli (SDOF) kütle-yay-sönümleyici model
olarak idealize edilmiştir. u(t) fonksiyonu p(t) kuvveti etkisindeki sistemin
yerdeğiştirme tepkisini göstermektedir.
Figure. p(t) dış kuvveti etkisindeki tek serbestlik dereceli sistem
2. Tek-Serbestlik-Dereceli-Sistemler (SDOF)
Yapılan idealleştirme çerçevesinde, yapının tüm kütlelerinin tek bir
noktada toplandığı ve kiriş rijit olarak kalırken, tüm deformasyonun
kolonlarda oluştuğu kabul edilmektedir. Kütlesiz kolonlar, sisteme
rijitlik kazandırmaktadır. Ayrıca, lineer dinamik analize olanak
vermesi nedeniyle, sönümün viskoz sönüm olarak ele alınması
yaygın olarak tercih edilen bir yöntemdir.
2.1. Hareket Denklemi için Dinamik Denge
(D’Alambert İlkesi)
Bu prensibe göre, atalet kuvveti olarak bilinen hayali bir kuvvetin dış
kuvvetlere ilave edilmesiyle, dikkate alınan sistem dinamik denge
konumuna ulaşmış olur.
Şekil. SDOF sistem için analitik model (mekanik sistem)
Bilindiği gibi yapı sistemlerinin çözümünde, sistemin serbest cisim
diyagramı çizilir ve denge denklemi yazılır.
Aslında, D’Alambert
ilkesi de aynı prensibe sahip olup, tek fark dinamik denge
denkleminin yazılmasıdır.
2.1. Hareket Denklemi için Dinamik Denge
(D’Alambert İlkesi)
Serbest Cisim Diyagramı
p(t)
: dış kuvvet
fI(t)
: atalet kuvveti
fD(t)
: sönüm kuvveti
fS(t)
: yay (rijitlik) kuvveti
• Yay k rijitliğine sahip lineer bir yay olup, rijitlik kuvveti olarak bilinen ku
kuvvetini ortaya çıkarmaktadır.
fS
1
fS(t)=ku(t)
k
u
(2.1.1)
2.1. Hareket Denklemi için Dinamik Denge
(D’Alambert İlkesi)
• Sönümleyici, viskoz türde bir sönümleyici olup,
olmaktadır.
f D (t) cu (t) burada
du
dt
u
cu sönüm kuvvetine neden
(velocity )
(2.1.2)
fD
1
c
Bir kütlenin sıvı içindeki hareketine karşı oluşacak tepkiye benzer biçimde,
sönüm kuvvetini kütlenin hızıyla orantılı olarak kabul eden viskoz sönüm
modeli, doğrusal modele olanak sağladığı için dinamik hesaplarda en sık
kullanılan sönüm modelidir
2.1. Hareket Denklemi için Dinamik Denge
(D’Alambert İlkesi)
• Atalet kuvveti kütle ile ivmenin çarpımına eşittir ve sistemin hareket yönüne
ters yönde etkimektedir.
d 2u
f I (t) mü(t) burada ü 2 (accelerati on) (2.1.3)
dt
Bu durumda, hareket
edilmesinden ibarettir.
denklemi
bu
kuvvetlerin
f I (t) f S (t) f D (t) p(t)
dengesinin
ifade
(2.1.4)
(2.1.1-2.1.3) denklemleri, (2.1.4) denkleminde yerine yazılırsa, tek
serbestlik dereceli sistemin hareket denklemi elde edilir.
mü cu ku p(t)
(2.1.5)
2.2. Hareket Denklemi için Newton’un İkinci
Hareket Kanunu
Serbest Cisim Diyagramı
Net kuvvet (p(t)- fS(t)- fD(t)) olduğuna göre,
Newton’un ikinci hareket kanunu yazılacak
olursa,
p(t) - f S (t) f D (t) mü
(2.2.1)
mü cu ku p(t)
(2.2.2)
2.2. Hareket Denklemi için Newton’un İkinci
Hareket Kanunu
mü cu ku p(t)
Elde edilen hareket denklemi, sabit katsayılı ikinci dereceden lineer
bir diferansiyel denklemdir. Statik problemin çözümü bilindiği gibi
cebrik bir denklem yazılmaktadır. Ancak, dinamik yük etkisindeki bir
sistemin çözümünde söz konusu cebrik denklem, ikinci dereceden
bir diferansiyel denkleme dönüşmektedir. İkinci dereceden
diferansiyel denklem çözümünün, statik problemin cebrik
denkleminin çözümünden daha karmaşık olduğu bilinen bir
gerçektir.
Tek Serbestlik Dereceli Sistemin Hareket Denklemi
Tek serbestlik dereceli sistemin hareket denkleminin elde edilmesi
için aşağıdaki çerçeve sistem ele alınsın.
Sistemde kolonların eksenel rijitliği sonsuz iken, kiriş eksenel ve
eğilme rijitlikleri sonsuzdur. Kiriş tamamen rijit ve kolonlar eksenel
olarak rijit olduğundan, sisteme düşey ağırlık kuvvetlerinin etkimesi
durumunda, söz konusu kuvvetler doğrudan tabana aktarılacaktır. Bu
durumda, yapıda yerdeğiştirme oluşturacak tek yükleme durumu,
yatay yükleme durumudur. Sistemin yatay rijitliği, tamamen eğilme
etkisindeki kolonların rijitliği ile sağlanmaktadır.
Mukavemet bilgileri ışığında;
Şekil. Dört kolona oturan rijit platform (a) Sistem (b) Deplasman yapmış
kolona etkiyen kuvvetler (c) Kütleye etkiyen yatay kuvvetler
Tek Serbestlik Dereceli Sistemin Hareket Denklemi
Kütleye ait serbest cisim diyagramı çizilir ve herhangi bir t anında rijit
kütleye etkiyen kuvvetler gösterilirse,
Net kuvvet (p(t)- fS(t)- fD(t)) olduğuna göre, Newton’un ikinci hareket
kanunu yazılırsa,
p(t) -
12 EI
12 EI
u
u f D (t) mü
L3
L3
(2.2.4)
Sönüm kuvveti de f D (t) cu (t) dahil edilirse
mü cu
24 EI
u p(t)
3
L
(2.2.5)
Tek Serbestlik Dereceli Sistemin Hareket Denklemi
k
24EI
L3
olduğuna göre, hareket denklemi
mü cu ku p(t)
(2.2.6)
Yay Rijitlikleri
Kolonlarda gösterilen k1 ve k2 rijitlikleri, her bir kolonun u ile gösterilen
serbestlik yönünde harekete karşı direncini temsil etmektedir. Eğer her iki
kolonun da aynı anda aynı yatay ötelenmeyi yapacağı varsayılırsa, sistemin
toplam rijitliği k=k1+k2 olur. Bir yapı içinde bulunabilecek değişik elemanları
yansıtmak için, gerekirse modelde birden fazla yay da kullanılabilir. Gerçek
yapılardaki kiriş gibi elemanların rijitliği de kullanılan malzemeye bağlı olarak
statik hesap yöntemleri ile hesaplanır. Birden fazla yay veya yapı elemanının
bulunduğu daha karmaşık sistemlerde modelin rijitliğini tek bir sabitle belirtmek
için, eşdeğer yay sabiti denen ke oluşturulabilir (Tablo 2.2.1-2.2.2).
Yay Rijitlikleri
Sistem (Model)
Eşdeğer Yay Sabiti
ke k
ke
1
n
k
i 1
i
n
ke ki
i 1
Tablo 2.2.1 Çeşitli yay sistemleri için eşdeğer yay sabitleri
Eşdeğer Yay Sabitleri
Sistem (Model)
Eşdeğer Yay Sabiti
PL3
48 EI
1 P k
48 EI
k 3 ke
L
ke
3EI
L3
Tablo. Yapı modellerinde kullanılan bazı doğrusal-elastik elemanların
eşdeğer yay sabitleri
2.3. Hareket Denklemi: Ağırlık Kuvvetleri
2.3. Hareket Denklemi: Ağırlık Kuvvetleri
Serbestlik derecesi doğrultusunda ağırlık kuvvetleri elde etmek için, yaykütle sisteminin 90 döndürülmesiyle elde edilen yukarıdaki sistem ele
alınsın. Rijit kütlenin ağırlığı W, (2.2.6) denkleminin sağ tarafına eklenirse;
f I (t) f S (t) f D (t) p(t) W
mü t (t ) cu t (t ) kut (t ) p(t) W
(2.3.1)
(2.3.2)
Toplam yerdeğiştirme ut, W ağırlığından ortaya çıkan ust statik
yerdeğiştirmesi ile, dinamik kuvvetin neden olduğu u yerdeğiştirmesinin
toplamına eşit olması durumunda,
u t (t ) u(t) u st
u t (t ) u (t)
ut (t ) u(t)
(2.3.3)
2.3. Hareket Denklemi: Ağırlık Kuvvetleri
Elastik kuvvet,
f S (t) kut (t) kust ku(t )
(2.3.4)
(2.3.3) ve (2.3.4) denklemleri , (2.3.2) denkleminde yerine yazılırsa,
mü(t ) cu (t ) kust ku(t ) p(t) W (2.3.5)
kust=W, olduğuna göre
mü(t ) cu(t ) ku(t ) p(t)
(2.3.6)
Statik denge konumunun esas alınarak yazılması durumunda, lineer
elastik bir sistemin hareket denklemi, ağırlık kuvvetlerinden
etkilenmeyecektir.
Örnek: Konsol bir kiriş ucundaki yaya asılı w ağırlığının hareket
denklemini elde ediniz. Yayın ve kirişin kütlesini ihmal ediniz. E=204000
N/mm2.
Fig. (a) Sistem; (b) deforme olmamış, deforme olmuş, ve statik denge
konumları; (c) serbest-cisim diyagramı; (d) yay ve kiriş kuvvetleri
2.4. Hareket Denklemi: Deprem Etkisi
Şekilde görüldüğü gibi yapı sistemine doğrudan etkiyen bir dış
kuvvet bulunmamaktadır. Yapıdaki yerdeğiştirme ve gerilmeler,
deprem
nedeniyle
mesnet
noktalarının
hareketinden
kaynaklanmaktadır. Burada sabit referans eksene göre ug(t) rölatif
yer hareketi ile tanımlanan deprem hareketinin sadece yatay
bileşeni dikkate alınacaktır.
Mesnet hareketinin tek serbestlik dereceli sistemin dengesine etkisi: (a)
sistemin hareketi; (b) denge kuvvetleri
2.4. Hareket Denklemi: Deprem Etkisi
Burada, kirişin rijit olduğu ve hareket eden tüm kütleyi içerdiği
kabul edilirken, düşey kolonlar kütlesiz ve eksenel olarak rijit kabul
edilmektedir. Her bir kolonun eğilme rijitliği k/2 olarak
tanımlanırken, kütlenin tek bir serbestlik derecesi ,u(t), söz konusu
olmaktadır. Bunun yanında, c sönümleyicisi de serbestlik derecesi
doğrultusunda harekete ters yönde ve hızla orantılı olan bir direnç
oluşturmaktadır.
Rijit bir temel için sistemin tabanındaki yerdeğiştirme ug(t) olarak
tanımlanırken, söz konusu yerdeğiştirme tabliye hizasında
toplanan kütlenin tabana göre rölatif yerdeğiştirme u(t)
yapmasında neden olmaktadır.
2.4. Hareket Denklemi: Deprem Etkisi
Tabliye hizasında toplam yerdeğiştirme,
u t (t ) u g (t ) u(t )
(2.4.1)
Kütlenin serbest cisim diyagramı dikkate alınırsa,
f I (t) f S (t) f D (t) 0
(2.4.2)
Elastik ve sönüm kuvvetleri (2.1.1) ve (2.1.2) denklemleri ile verilirken,
atalet kuvveti, toplam ivmeye bağlı olarak aşağıdaki gibi
tanımlanmaktadır.
f I (t) mü t (t)
(2.4.3)
Bu ifadeler, (2.4.2) denkleminde yerine yazılırsa,
2.4. Hareket Denklemi: Deprem Etkisi
mü t (t ) cu (t ) ku(t ) 0
ü t (t ) ü(t ) üg (t ) (2.4.5)
(2.4.4)
olduğuna göre, (2.4.5) ifadesi (2.4.4) denkleminde
yerine yazılırsa,
mü(t ) müg (t ) cu (t ) ku(t ) 0
(2.4.6)
üg(t) eşitliğin sağ tarafına atılarak, deprem hareketi etkisindeki tek
serbestlik dereceli bir sistemin hareket denklemi elde edilir.
mü(t ) cu (t ) ku(t ) peff (t )
peff (t ) müg (t )
(2.4.7)
(2.4.8)
2.4. Hareket Denklemi: Deprem Etkisi
peff(t), deprem hareketinin yapı üzerindeki etkisine eşdeğer olan, etkin
sismik kuvveti ifade etmektedir. Başka bir ifade ile, üg(t) yer hareketi
etkisindeki yapı sisteminin u(t) yerdeğiştirmesi , zemine ankastre ve kütle
ile yer hareket ivmesinin çarpımına eşit ve ters yönde uygulanan dış
kuvvet etkisindeki aynı yapı sisteminin yerdeğiştirmesi ile aynı olacaktır.