fonksiyonların limiti 02

DİZİLER YARDIMIYLA LİMİT
Görüntüler Dizisi
Tanım: A  R olmak üzere, f : A  R fonksiyonu verilmiş olsun.
Terimleri A kümesinin elemanı olan bir (x n ) dizisi için (f(x n ))
dizisine; (x n ) dizisinin f fonksiyonuna göre görüntü dizisi denir.
(x n )  (x1 , x 2 , x 3 ,...., x n ,....) dizisi için, (f(x n )) görüntü dizisi;
(f(x ))  (f(x ), f(x ), f(x ),.....f(x ),....) dir.
n
1
2
3
n
bitir
ÖRNEK
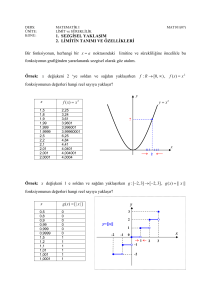
 1  dizisi ve f(x)=2x+3 fonksiyonu veriliyor:
(x n )  1  
 n
a) (x n ) dizisinin limitini bulalım. (lim n  (x n ))
b) (f(x n )) görüntüler dizisini bulalım.
c) (f(x n )) görüntüler dizisinin limitini bulalım.
(lim n  (x n ))
bitir
ÇÖZÜM
a)
 1
lim n  (x n )  lim n  1    1 dir.
 n
  1  
2
b) (f(x n ))  (2(x n )  3)   21    3    5   bulunur.
n
  n  
2

c) lim n  (f(x n ))  lim n   5    5 bulunur.
n

bitir
BİR FONKSİYONUNUN LİMİTİ
Tanım: A  R, a  R, L  R olmak üzere, f : A  R ya da
f : A - a  R fonksiyonu verilmiş olsun. Terimleri A - a
kümesinde bulunan ve a’ya yakınsayan her (x n ) dizisi için,
(f(x n )) dizileri bir L sayısına yakınsıyorsa; x, a’ya giderken
f(x)’in limiti L’dir, denir ve (lim x a f(x)  L biçiminde
gösterilir.
Limitin Olmaması:
Terimleri A - a kümesine ait ve a’ya yakınsayan en az iki (x n )
,
(x
ve n ) dizileri için (lim f(x n )  (lim f(x ,n ) ise x  a için
f fonksiyonunu limiti yoktur.
bitir
ÖRNEK
f : R  R, f(x)  3x - 4
limitini bulalım.
fonksiyonunun x 1
bitir
için
ÇÖZÜM
Terimleri 1’den farklı ve 1’e yakınsayan iki dizi seçelim.
 1 ,
 1
(x n )  1  , (x n )  1   dizilerinin f fonksiyonu ile elde
 n
 n
edilen görüntü dizilerinin limitlerini alalım.
  1 
  1 
,
(f(x n ))   31    4   1, (f(x n ))   31    4   1
  n 
  n 
O halde, limiti 1 olan her (x n ) dizisi için,
(f(x n ))  (3x n  4)  3  4  1
bitir
EPSİLON TEKNİĞİ İLE LİMİT
Tanım: A  R, f : A  R bir fonksiyon a  R, L  R,   R 
olmak üzere x - a    f(x) - L   önermesine uyan
a
bağlı   R  varsa x, a’ya yakınsarken f’nin limiti L’dir denir
ve (lim x a f(x)  L biçiminde yazılır.
Tanımı aşağıdaki şekiller üzerinde inceleyiniz.

y=f(x)
y=f(x)
y=f(x)
L
L
L 
L
f(x)
f(x)
L 
x
0
a -
L
f(x)
L
a 
L 
x
0
f(x)
L
f(x)
x
a
f(a)
a -
f(x)
x
a
x
a 
0
bitir
a -
x
a
a 
ÖRNEK
f : R  R , f(x)  2x - 1fonksiyonu veriliyor.
lim x 2f(x)  3
olduğunu epsilon tekniği ile gösterelim.
bitir
ÇÖZÜM
  0
  0
içinX - 2    f x   3  
bulmalıyız.
önermesine uyan
   x - 2  
 -2  2x - 4  2
 2  2x -1- 3  2
 -2  f(x) - 3  2
X-2 
 f x   3  2

O halde   2
alınabilir.   0 İçin,
tanıma göre lim x 2 f(x)  3 olur.

bitir

2
 0 olduğundan
SOLDAN VE SAĞDAN LİMİT
f : R  R ya da f : R - a  R şeklinde tanımlı f
fonksiyonunda:
Tanım1: x değerleri a dan küçük değerlerle artarak(soldan)a ya
yaklaşırken,f(x) ler de bir L1 reel sayısına,f fonksiyonunun a
noktasındaki soldan limiti denir ve lim x a - f(x)  L1
biçiminde gösterilir.
Tanım2:x değerleri a dan büyük değerlerle azalarak (sağdan) a ya
yaklaşırken f(x) ler de bir L 2 reel sayısına yaklaşıyorsa;
reel sayısına,f fonksiyonunun a noktasındaki sağdan limiti denir
ve lim
. xa   L 2 biçiminde gösterilir.
1.
2.
X  a-
yazılışı x lerin a ya soldan yaklaştığını gösterir.yani
daima x<a dır.
xa

yazılışı x lerin a ya sağdan yaklaştığını gösterir.yani
daima x>a dır.
bitir
Şekildeki grafiklerde , x in a ya soldan ve sağdan yaklaşması
durumunda soldan ve sağdan limitleri görülmektedir.
y
y
L1
L2
a
X
X
a
Sonuçlar: lim x a -f(x)  L1 ve lim xa   L 2
1. L1  L2  L  R ise, lim x a f(x)  L
1  L2
L
2.
dir.
ise lim xa f(x) yoktur.
bitir
için;
Aralığının uç noktalarındaki limiti
f : a, b  R, y  f x 
fonksiyonunun tanım aralığının uç
noktalarındaki limiti araştırılırken:
1.a noktasındaki limit sadece sağdan limitle belirlenir.
lim x a f x   lim xa  f x   P  f a 
2.b noktasındaki limit, sadece soldan limitle belirlenir.
lim x b f x   lim x b f x   K  f b 
yy
K=f(b)
y=f(x)
P=f(a)
x
a
0
b
bitir
f : a, b  R, y  f x 
fonksiyonunun tanım
aralığının uç noktalarındaki limiti araştırılırken:
1.a noktasındaki limit,sadece sağdan limitle belirlenir.
lim x a f x   lim x a  f x   P dir.f(a) tanımsızdır.
2.b noktasındaki limit sadece soldan limitle belirlenir.
lim x b f x   lim x b f x   K dir. f(b) tanımsızdır.
yy
y=f(x)
K
P
x
a
0
b
bitir
ÖZEL TANIMLI FONKSİYONLARIN LİMİTLERİ
PARÇALI FONKSİYONLARIN LİMİTLERİ
gx , x  a ise
f x   
h x , x  a ise
fonksiyonu verilsin.
Kritik noktada,yani koşuldaki x  a değerinde limit sorulursa,soldan ve
sağdan limit incelenir.
lim x a  f x   lim x a  gx   L1 

lim x a  f x   lim x a  h x   L 2 
L1 ve L2 ye göre cevaplama yapılır.
Kritik nokta dışında limit sorulursa o noktadaki fonksiyon dalı belirlenir.o
dalın durumuna göre çalışma yapılır.
x1  a
için
x2  a
için
lim x x1 f x   lim x x1 gx 
lim x x 2 f x   lim xx 2 h x 
bitir
ÖRNEK:
f : R  
1 R
fonksiyonunun
 x  1, x  1
f x   
x  1, x  1
x  1, x  2
ve
ise
ise
x  2
noktalarındaki limiti bulalım.
bitir
ÇÖZÜM:
lim x 1 f x   lim x 1  x  1  0

lim x 1 f x   lim x 1 x  1  0  olduğundan
lim x 2 f x   lim x 2  x  1  3

lim x 2 f x   lim x 2  x  1  3
lim x 2 f x   lim x 2 x  1  1

lim x 2 f x   lim x 2 x  1  1



olduğundan
lim x1 f x   0 dır.
lim x 2 f x   3 tür.
olduğundan lim x2 f x   1 dir.
bitir
MUTLAK DEĞERLİ FONKSİYONLARIN LİMİTİ
f : R  R, lim xa f x 
in bulunuşunda:
x  a noktası kritik nokta f a   0 ise, soldan ve
sağdan limit incelenmelidir.
Limit sorulan nokta kritik nokta değilse,
değeri ile görüntü olacağından
f a   0
lim xa f x   f a  dır.
bitir
limit
ÖRNEK:
f : R   2,2  R , f x  
x 4
.
2
2 x
fonksiyonunun;
x  2, x  0, x  2 ve x  4 noktalarında limitinin
olup olmadığını araştıralım.
bitir
ÇÖZÜM:
f(X) fonksiyonunu tablo yardımıyla parçalı fonksiyon şeklinde
yazalım.
x
x2  4
x
f x 

-2
+
-
-
x2  4
4  x2
 x2
 x  2
2 x
2x
x  2, x  2
 x  2,2  x  0

f x   
x  2,0  x  2
 x  2, x  2

2
0
+
+
+
x2  4
4  x2
 x  2
 x  2
2x
2x
ise
ise
ise
ise
bitir
a. lim x 2 f x   lim x 2 x  2  4 



lim x 2 f x   lim x 2  x  2   4
lim x2 f x 
yoktur.
b. lim x 0 f x   lim x 0  x  2   2

 lim x0 f x   2 dir.
lim x 0 f x   lim x 0 x  2  2 

c. lim
f x   lim x 2 x  2   4
x 2 

 lim x2 f x  yoktur.
lim x 2 f x   lim x 2  x  2   4
d. lim x 4
x2  4
2 x
 f 4 
12
6
2
bulunur.
bitir
İŞARET (sgn) FONKSİYONUNUN LİMİTİ
f : R  R, lim xa sgn f x  nın bulunuşunda:
1.
noktası kritik nokta f a   0 ise, bu noktalarda soldan
ve sağdan limit incelenmelidir.
x a
lim x a  sgn f x   L1
Eğer L  L ise
1
2
ve
lim x a  sgn f x   L 2 olsun
lim xa sgn f x   L1  L2 dir.
Eğer L1  L2 ise lim xa sgn f x  yoktur.
2. Limiti sorulan nokta kritik nokta değilse
f a   0
Limit değeri ile görüntü değeri eşit olacağından,
lim xa sgn f x   sgn f a  dır.
bitir
ÖRNEK:


f : R  R, f x   sgn x  3
fonksiyonunun, x  3
noktalarındaki limitinin olup olmadığını araştıralım.
bitir
ÇÖZÜM:
lim x 3 f x   lim x 3 1  1
 olduğundan,
lim x 3 f x   lim x 3 1  1
lim x3 f x   1
y
1
0
1
2
3
x
-1
bitir
TAM KISIM FONKSİYONUN LİMİTİ
f : R  R, lim xa f x 
ın bulunuşunda:
x  a için f a  Z ise, soldan ve sağdan limit incelenir.
Soldan limit incelenirken,yani h    0 olmak üzere,
x  a  h yazabiliriz.Sonra h  0 için limitini alabiliriz.
lim xa  f x   lim h0 f a  h   L1
Sağdan limit incelenirken x  a olduğundan,yani h    0
olmak üzere x  a  h yazabiliriz.
Sonra h  0 için limitini alabiliriz.
lim xa  f x   lim h0 f a  h   L2
Eğer L1  L2  L  lim xa f x   L dir.
Eğer L  L  lim
dir.
1
2
x a f x 
bitir
x  a için f a  Z ise, limit değeri ile görüntü değeri eşit
olacağından;
lim xa f x   f a 
dir.
ÖRNEK:
f x   2x  1
1
fonksiyonunun x 
2
3
ve x 
5
noktalarında limitlerinin olup olmadığını inceleyelim.
bitir
1
ÇÖZÜM: a. x 
için, 2x  1   1   1  0  Z olduğundan fonksiyonun
2
2
soldan ve sağdan limitini inceleyelim.
1
Soldan limit incelerken, x 
olduğundan, yani h    0
2
1
olmak üzere x   h yazalım ve h  0 için limitini alalım.
2

lim  1  f x   lim h0 
x  

2 

1

2  h   1  lim h0  1  2h  1  0  1  1
2


Sağdan limit incelenirken, x  1 olduğundan, yani h    0
2
1
Olmak üzere, x 
yazalım ve h  0 için limitini alalım.
2h

lim  1  f x   lim h0 
x  

2 

1

2  h   1  lim h0  1  2h  1  1  1  0
2


bitir
1
x
2
noktasında soldan ve sağdan limitler farklı olduğundan;
lim
b. x  3
5
1
x
2
f x 
yoktur.
1
3
için, 2x  1  2   1   Z olduğundan, limit
5
5
değeri ile görüntü değeri eşit olur.
6
3
3
1  1 1  0
O halde, lim 3 f x   f    2   1 
x
5
5
5
5
bitir
SONSUZ İÇİN LİMİT
bir fonksiyon olsun.Terimleri x 0 , 
aralığında bulunan ve   a ıraksayan her x n  dizisi
lim n f x n   L
için,
ise;
için,
x  
f ninlim
limiti
ve
biçiminde
f dir,
x  denir
L
n  L
gösterilir.
f : x 0 ,  R
Aynı şekilde f :  , x 0   R bir fonksiyon olsun.
Terimleri  , x 0  aralığında bulunan ve   a
ıraksayan her x n  dizisi için lim n f x n   K ise;
için, f nin limiti K dır, denir ve lim n f x   K biçiminde
gösterilir.
bitir
ÖRNEK:
a.
1
 ,x  0
f : R  R , f x    3
3, x  0
lim x f x 
b.
ise
ise
fonksiyonu veriliyor.
lim x f x 
ifadelerinin eşitini bulalım.
bitir
ÇÖZÜM:
a. x n  dizisi için,
lim x n    olsun.
 1 
1


lim x f x   lim n f x n   lim n   
 0 dır.
 xn   
b.
x n 
dizisi için, lim x n    olsun.
 1 
1
lim x f x   lim n f x n   lim n   
 0 dır.
 xn   
bitir
SONSUZ LİMİT
A  R ve a  A olmak üzere, f : A  R ya da
f : A  a  R fonksiyonu için , terimleri; A  a
kümesine ait ve a sayısına yakınsayan x n  dizisi için, x n  0 :
ise, lim xa f x   
1. f x n   
2. f x n    ise,
y
a
0
lim xa f x   
dur.
xx
bitir