6−II. DERECEDEN FONKSÝYONLAR−2(Parabol) (Grafikten Parabolün Denklemi-Parabol ve Doðru) LYS MATEMATÝK
1.
f(x)
O
−2
y
4.
y
f(x)
x
3
−8
−6
x
4
O
T
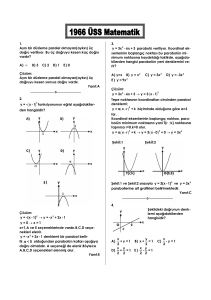
Yukarıda grafiği verilen y = f(x) parabolünün
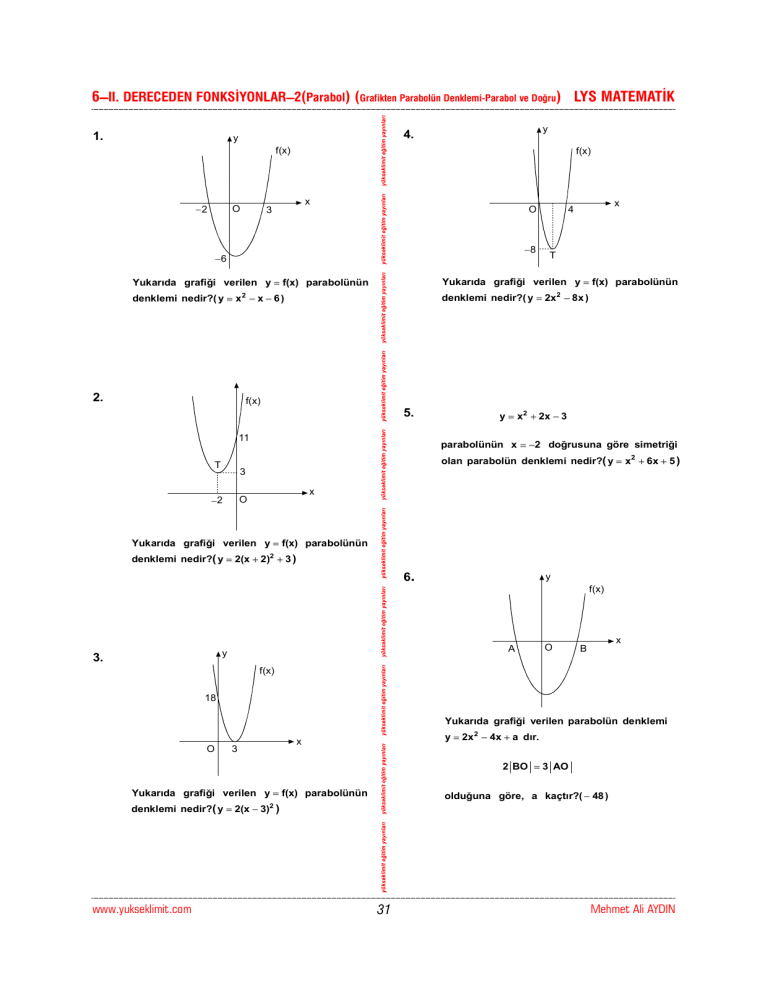
Yukarıda grafiği verilen y = f(x) parabolünün
denklemi nedir?( y = x 2 − x − 6 )
denklemi nedir?(
=
y 2x 2 − 8x )
2.
f(x)
5.
11
T
parabolünün x = −2 doğrusuna göre simetriği
olan parabolün denklemi nedir?( y = x2 + 6x + 5 )
3
x
O
−2
y = x2 + 2x − 3
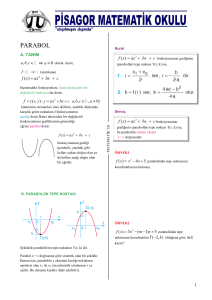
Yukarıda grafiği verilen y = f(x) parabolünün
denklemi nedir?( y = 2(x + 2)2 + 3 )
6.
A
y
3.
y
O
f(x)
x
B
f(x)
18
Yukarıda grafiği verilen parabolün denklemi
O
3
y = 2x2 − 4x + a dır.
x
2 BO = 3 AO
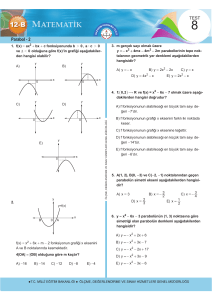
Yukarıda grafiği verilen y = f(x) parabolünün
olduğuna göre, a kaçtır?( − 48 )
( y 2(x − 3)2 )
denklemi nedir?=
www.yukseklimit.com
31
Mehmet Ali AYDIN
6−II. DERECEDEN FONKSÝYONLAR−2(Parabol) (Grafikten Parabolün Denklemi-Parabol ve Doðru) LYS MATEMATÝK
10.
y = x2 + x − 6
y =− x + 2
7.
Yukarıda denklemleri verilen parabol ve doğ runun kesiştiği noktaların koordinatları ne -
k
x
y= x − 4
y=
Yukarıda denklemleri verilen eğri ile doğ ru teğet olduğuna göre, k kaçtır?( − 4 )
dir?( A(−4,6) ve B(2,0) )
y
11.
16
8.
y=
− x2 + 10
a)
A
=
y x 2 − 22
O
6
Yukarıda denklemleri verilen parabollerin
kesişme noktalarının arasındaki uzaklık
x
g(x)
f(x)
kaç birimdir?(8 )
8
Yukarıda grafiği verilen f(x) parabolü ile g(x)
doğrusunun teğet olduğu A noktasının koor dinatları nedir?( A(4,8) )
b)
=
y x 2 − 10
y= x + 2
Yukarıda denklemleri verilen parabol ve
doğrunun kesiştiği noktaların arasın -
12.
daki uzaklık kaç birimdir?(7 2 )
y
T
x
O
f(x)
9.
y = x 2 + 5x + a
y= x − 4
Yukarıda grafiği verilen f(x) = ax 2 + bx + c pa rabolüne göre, aşağıdakilerden hangisi ke sinlikle doğrudur?
Yukarıda denklemleri verilen parabol ve doğ ru kesişmediğine göre, a hangi koşulu sağ lar?( a > 0 )
=
A) a + b + c 0
=
B) a − b + c 0
C) a • b • c > 0
D) a + c < 0
E) b + c > 0
www.yukseklimit.com
32
Mehmet Ali AYDIN
6−II. DERECEDEN FONKSÝYONLAR−2(Parabol) (Grafikten Parabolün Denklemi-Parabol ve Doðru) LYS MATEMATÝK
13.
16.
y=
− x2 + mx − 2
2
y=
x + 3mx + 2
y=
−x2 + 8
y 2x + 11
=
Yukarıda bir parabol ve bir doğrunun denk -
Yukarıda denklemleri verilen paraboller teğet
lemi verilmiştir.
olduğuna göre, m nin alabileceği değerlerin
çarpımı kaçtır?( − 8 )
Buna göre, parabolün doğruya en yakın o lan noktasının koordinatları nedir?( A(−1,7) )
14.
Parametrik denklemleri,
17.
x 2t + 1
=
=
y 2x − 1
=
y x2 + 6
2
y 4t − 14
=
Yukarıda bir doğru ve bir parabolün denk lemi verilmiştir.
olan parabolün ikinci açıortay doğrusu ile ke siştiği noktaların apsislerinin toplamı kaçtır?(1)
Buna göre, doğrunun parabole en yakın o lan noktasının
apsisi kaçtır?(
17
)
5
y
15.
f(x)
y
18.
y=2x 2
B
O
A
2
7
x
A
g(x)
B
2
O
Yukarıda grafikleri verilen parabol ve doğru nun kesiştiği noktaların apsislerinin çarpı mı kaçtır?(14 )
x
g(x)
Yukarıda grafikleri verilen parabol ve doğru nun kesişme noktalarının orta noktalarının
geometrik yer denklemi nedir?(
=
y 4x2 + 2 )
www.yukseklimit.com
33
Mehmet Ali AYDIN
6−II. DERECEDEN FONKSÝYONLAR−2(Parabol) (Grafikten Parabolün Denklemi-Parabol ve Doðru) LYS MATEMATÝK
19.
22.
x = y2 − 4y + 3
A(−1,7) , B(1,5) ve C(2,7) noktalarından geçen
parabolün denklemi nedir?(y = x 2 − x + 5)
bağıntısıyla tanımlanan eğrinin grafiği ne dir?
23.
y ≥ x 2 − 4x
y−x<0
20.
x = y2
koşullarını sağlayan noktaların grafiği ne -
− 32y =
x3
dir?
Yukarıda denklemleri verilen eğrilerin kesiş me noktaları nedir?( A(0,0) ve B(4, −2) )
24.
21.
y
a ,b ∈ R olmak üzere,
O
2
− a + 6a + 1
A=
A
B
x
B = 2b2 + 4b − 41
f(x)
olduğuna göre, A nın en büyük değeri ile
B
nin en küçük değerinin
toplamı
kaç -
Yukarıda grafiği verilen f(x) =
− x 2 + 8x + a
tır?( − 33 )
parabolünde
AB = 4 br
olduğuna göre,
f(x) in alabileceği kaç farklı doğal sayı
değeri vardır?( 5 )
www.yukseklimit.com
34
Mehmet Ali AYDIN
6−II. DERECEDEN FONKSÝYONLAR−2(Parabol) (Grafikten Parabolün Denklemi-Parabol ve Doðru) LYS MATEMATÝK
25.
28.
f(x) parabolü Ox eksenini − 2 ve 5 apsisli
f(10)
f(4)
noktalarda kestiğine göre,
ifadesinin
a ≠ 4 olmak üzere,
f(x) = (a − 4)x 2 + 5x + 3 − a
eşiti kaçtır?( − 10 )
parabollerinin geçtiği sabit noktalardan geçen
doğrunun denklemi nedir?(=
y 5x − 1)
26.
y= mx 2 + 4x + 2
parabolünün
y = −2
29.
doğrusuna
teğet
ol -
m nin hangi pozitif değeri için,
y =x2 + mx + 6
duğu noktanın orijine olan uzaklığı kaç br
dir?( 2 2 )
parabolüne orijinden çizilen teğetler dik ke sişir?( 23 )
y
27.
y
30.
f(x)
A
g(x)
x
O
B
O
A
x
Yukarıda grafikleri verilen y2 = 2x eğrisi ile
y =− x + 4 doğrusunun kesiştiği A ve B nok -
Yukarıda grafiği verilen f(x) = x 2 − 2x + 4
parabolü birinci bölgede hangi apsisli
A noktasında orijinden geçen g(x) doğ rusuna teğettir?( 2 )
talarının koordinatlarının toplamı kaçtır?(8 )
www.yukseklimit.com
35
Mehmet Ali AYDIN
6−II. DERECEDEN FONKSÝYONLAR−2(Parabol) (Grafikten Parabolün Denklemi-Parabol ve Doðru) LYS MATEMATÝK
y
31.
34.
f(x)
O B
a ≠ 0 olmak üzere,
f(x) = ax 2 + bx + c
f( −3 )= f(5 )= 0
a • f(α ) ≤ 0
x
C
olduğuna göre, α nın alabileceği değerlerin
A
toplamı kaçtır?( 9)
T
Yukarıda grafiği verilen f(x)=
parabolünün
tepe
eşkenar dörtgen
noktası
3 2
x − 3x + k
4
T ve TABC
olduğuna göre,
y
35.
T
taralı
A
alan kaç br 2 dir?(12 )
α
y
32.
x
B
g(x)
f(x)
10
x
O
Yukarıdaki grafikte tepe
2
noktası Oy üze 2
rinde olan f(x) = mx + (m − 4)x − 6m para bolü ile g(x) doğrusu verilmiştir.
T
AT
=
f(x)
AB
olduğuna
göre,
tanα
kaç -
tır?( − 2 3 )
Yukarıda grafiği verilen f(x) =
− x 2 + 4x + a
parabolünün tepe noktası T olduğuna
göre, f(a) kaçtır?( − 104 )
36.
y = x 2 − 4x − 12
parabolünün
33.
y = −6
doğrusuna
göre
simetriği olan parabolün denklemi ne -
y
dir?( y =
− x2 + 4x )
f(x)
A
TEST − 6 CEVAPLAR :
12) C
19
O
−1
3
y
x
3
2
−3
−1
B
1
x
O 3
g(x)
Yukarıda grafiği verilen doğru ile parabol
orijine göre simetrik olan A ve B nok talarında kesişmektedir.
23)
Buna göre, A ve B noktalarının ordinat -
O
ları arası uzaklık kaç br dir?( 4 3 )
www.yukseklimit.com
y
36
4
x
Mehmet Ali AYDIN
6−II. DERECEDEN FONKSÝYONLAR−2(Parabol) (Grafikten Parabolün Denklemi-Parabol ve Doðru) LYS MATEMATÝK
1.
y
Ox eksenini x1 ve x 2
apsisli noktalarda
kesen y = f(x) pa rabolünün denklemi ,
f(x) =a • (x − x1) • (x − x2 )
olduğundan,
−2
4.
f(x)
O
3
0+4
= 2 dir.
2
Tepe noktası T(r,k) olan
parabolün denklemi ,
x
f(x)= a • (x − r)2 + k dir.
f(x)
= 2x 2 − 8x elde edilir.
f(x)
11
T
−2
2
f(0) = a • (0 + 2) + 3
11 =
4a + 3 ⇒ a =
2 olur
y = x 2 + 2x − 3
parabolünün x = −2 doğrusuna göre simetriği
için ,
x = −2
x+2=
0
olduğundan verilen parabolde x yerine x + 2
yazılırsa
y = x 2 + 2x − 3
y = (x + 2)2 + 2(x + 2) − 3
3
O
T
f(x) = 2(x − 2)2 − 8
5.
f(x)= a • (x + 2)2 + 3
elde edilir.
f(0) = 11 olduğundan
−8
a 2=
elde edilir. a 2 yukarıda yazılırsa
=
f(x) = x − x − 6
elde edilir.
= a • (x − ( −2))2 + 3
f(x)
y = x2 + 6x + 5 elde edilir.
x
6.
y
f(x)
ve yukarıda yazılırsa
f(x) = 2(x + 2)2 + 3
elde edilir.
A
−2n
O
B
3n
x
y
3.
f(x)
Parabolün denklemi y = 2x 2 − 4x + a verilmiş.
18
2 BO = 3 AO
BO 3n
ve AO 2n alınırsa ,
=
=
O
3
x1 = −2n
x
x2 = 3n
kök olarak alınırsa ,
2x2 − 4x + a =
0
b
−
x1 + x 2 =
a
−4
− 2n + 3n = −
2
n = 2 elde edilir.
Böylece kökler x1 =
−4 ve x 2 =
6 elde edilir.
Tepe noktası T(r,k) olan parabolün denklemi ,
f(x)= a • (x − r)2 + k olduğundan
f(x) = a • (x − 3)2 + 0
f(0) = 18 olduğundan
f(0) = a • (0 − 3)2 + 0
18 = 9a
a = 2 elde edilir. a = 2 yukarıda yazılırsa
2x2 − 4x + a =
0
c
x1 • x 2 =
a
a
(−4) • 6 =
2
a = −48 elde edilir.
f(x)
= 2(x − 3)2
elde edilir.
www.yukseklimit.com
x
f(0) = 0 olduğundan
f(0) = a • (0 − 2)2 − 8
0 4a − 8
=
2
f(x)= a • (x − r)2 + k
olduğundan
4
O
f(x)= a • (x − 2)2 − 8
f(x) = a • (x + 2) • (x − 3)
elde edilir.
−6
f(0) = −6 olduğundan,
=
f(0) a • (0 + 2) • (0 − 3)
−6 =−6a ⇒ a =1 elde edilir ve yukarıda yazılırsa,
f(x) =1 • (x + 2) • (x − 3)
Tepe noktası T(r,k) olan
parabolün denklemi ,
f(x)
r
=
= a • (x − ( −2)) • (x − 3)
f(x)
2.
y
Tepe noktasının apsisi
31
Mehmet Ali AYDIN
6−II. DERECEDEN FONKSÝYONLAR−2(Parabol) (Grafikten Parabolün Denklemi-Parabol ve Doðru) LYS MATEMATÝK
7.
y =x 2 + x − 6 ve y =− x + 2
Parabol ile doğrunun kesiştiği noktaların
10.
x 2 + x − 6 =− x + 2
apsislerini veren denklem
ru teğet olduğuna göre,
k
= x−4
x
2
x − 4x − k =
0
denklemi için ∆ =0 olmalıdır.
2
⇒ x + 2x =
− 8 0 ⇒ (x + 4)(x −=
2) 0 ise
x=
−4 veya x =
2 tür.
Ordinatları bulmak için yukarıdaki fonksiyon lardan birini örneğin y =− x + 2 yi kullanırsak ,
x = −4 için y = −(−4) + 2 ⇒ y = 6
x =2 için y =−2 + 2 ⇒ y =0 elde edilir.
Kesişme noktaları A(−4,6) ve B(2,0) dır.
8.
a)
∆ = b2 − 4ac = 42 − 4 • 1 • (−k) = 0
⇒ k = −4 elde edilir.
11.
Parabol ile doğrunun kesiştiği noktaların
⇒
=
y ax2 − 6ax olur.
Doğrunun denklemi ,
x
y
+
=
1
8 16
O
⇒y=
−2x + 16
Doğru ile parabol teğet
f(x)
olduğuna göre ,
apsislerini veren denklem, − x 2 + 10 = x2 − 22
⇒ 2x2=
− 32 0 ⇒ 2 • (x − 4)(x=
+ 4) 0
Buradan x = 4 ve x = −4 bulunur.
Ordinatları bulmak için yukarıdaki fonksiyon 2
lardan birini örneğin =
y x − 22 yi kullanırsak ,
x=
−4 için y =
(−4)2 − 22 ⇒ y =
−6
x=
4 için y =
42 − 22 ⇒ y =
−6 elde edilir.
(−4 − 4)2 + (−6 − (−6))2
−1 için
a=
elde edilir.
⇒ x 2 − x −=
12 0 ⇒ (x − 4)(x +=
3) 0
Buradan x = 4 ve x = −3 bulunur.
Ordinatları bulmak için yukarıdaki fonksiyon lardan birini örneğin y= x + 2 yi kullanırsak ,
x=
4 için y =
4+2⇒y=
6
ax2 − (6a − 2)x − 16 =
0
12.
x=
−3 için y =−
( 3) + 2 ⇒ y =
−1 elde edilir.
y
T
Kesişme noktaları A(4,6) ve B(−3, −1) dir.
A(x1, y1 ) ve B(x 2 , y2 ) noktaları arası uzaklık
c
(x1 − x 2 )2 + (y1 − y2 )2 dir.
x1
A(4,6) ve B( −3, −1) noktaları arası uzaklık
9.
(4 − (−3))2 + (6 − (−1))2
elde edilir.
r
x2
x
f(x)
f(x) = ax 2 + bx + c
kollar aşağı ⇒ a < 0 dır.
b
−
< 0 ⇒ b < 0 dır.
r=
2a
f(0)= c > 0 dır.
Sonuç olarak a < 0 , b < 0 , c > 0 olduğundan
C şıkkındaki a • b • c > 0 kesinlikle doğrudur.
y =x 2 + 5x + a ve y =x − 4
Parabol ile doğru kesişmediğine göre,
x 2 + 5x + a =x − 4
x 2 + 4x + a + 4 =
0
denklemi için ∆ < 0 olmalıdır.
∆= b2 − 4ac= 42 − 4 • 1 • (a + 4) < 0
⇒ a > 0 elde edilir.
www.yukseklimit.com
g(x)
− x2 + 8x − 16 =
0
− (x − 4) • (x =
− 4) 0 ve
=
x 4 elde edilir.
x = 4 ise y =
−2x + 16 ⇒ y =
−2 • 4 + 16 =
8 dir.
O halde teğet nokta K(4,8) dir.
1
−
a=
için x =
12 > 6 olduğundan imkansızdır.
9
apsislerini veren denklem , x 2 − 10 =x + 2
AB = 7 2 br
x
=
+ 1 0 ⇒ (9a + 1) • (a=
+ 1) 0
9a2 + 10a
1
−
−1 elde edilir.
Buradan a =
ve a =
9
Parabol ile doğrunun kesiştiği noktaların
=
AB
8
=
∆ (6a − 2)2 − 4 • a • (−16) ⇒ 0 = 36a2 + 40a + 4
(x1 − x 2 )2 + (y1 − y2 )2 dir.
y=
x2 − 10 ve y =
x+2
AB =
x 6
=
− 2)x − 16 0 denklemi
=
ax2 − (6a
için ∆ 0 dır.
A(−4, −6) ve B(4, −6) noktaları arası uzaklık
b)
A
−2x + 16
ax − 6ax =
A(x1, y1 ) ve B(x 2 , y2 ) noktaları arası uzaklık
AB = 8 br
16
2
Kesişme noktaları A(−4, −6) ve B(4, −6) dır.
AB =
y
Parabolün denklemi ,
=
y a • x • (x − 6)
y=
− x2 + 10 ve y =
x 2 − 22
AB =
k
ve y= x − 4
x
Yukarıda denklemleri verilen eğri ile doğ y=
32
Mehmet Ali AYDIN
6−II. DERECEDEN FONKSÝYONLAR−2(Parabol) (Grafikten Parabolün Denklemi-Parabol ve Doðru) LYS MATEMATÝK
13.
16.
y=
− x2 + mx − 2
y=
x 2 + 3mx + 2
Paraboller teğet olduğuna göre ,
2
apsisi için türevler alınıp eşitlenir.
y=
− x 2 + 8 ⇒ y' =
−2x
2
− x + mx − =
2 x + 3mx + 2
y=
2x + 11 ⇒ y' =
2
x −1 elde edilir.
⇒ −2x
= 2⇒=
Ordinatı bulmak için x = −1 parabolde
2x2 + 2mx + 4 = 0
denklemi için ∆ =0 olmalıdır.
Böylece
=
⇒ ∆ (2m)2 − 4 • 2 • 4
yazılmalıdır. Yani
=
⇒
0 4m2 − 32
c
⇒ m1 • m=
=
2
a
−32
⇒ m1 • m2 =
= −8 elde edilir.
4
14.
⇒ y = − x 2 + 8 ⇒ y = −(−1)2 + 8 ⇒ y = 7 elde edilir.
O halde parabolün doğruya en yakın noktası
A(−1,7) dir.
17.
noktanın apsisi için türevler alınıp eşitlenir.
=
y 4t 2 − 14 verilmiş.
x −1
O halde , x =+
2t 1 ⇒ t =
2
=
y 2x − 1 ⇒ y' = 2
y =+
x2 6 ⇒ y' =
2x
=
⇒ x 1 elde edilir.
Böylece ⇒
2x 2=
Ordinatı bulmak için x = 1 parabold yazılmalıdır.
2
x −1
=
y 4
− 14
2
x2 6 ⇒ y =
12 + 8 ⇒ y =
7 elde edilir.
⇒ y =+
O halde parabolün doğruya en yakın noktası
y = x 2 − 2x − 13 parabolün denklemi
y = − x ikinci açıortay doğrusunun denklemi
A(1,7) dir. Şimdi bu noktadan geçen ve
=
y 2x − 1 doğrusuna dik olan doğrunun
denklemini bulalım.
y=
2x − 1 eğim =
2
Parabolün ikinci açıortay doğrusu ile kesiştiği
noktaların apsislerini veren denklem ,
x2 − 2x − 13 =
−x
1
2
ve geçtiği nokta A(1,7) olduğundan
y−7
1
denklem
elde edilir.
= −
x −1
2
y−7
1
Böylece
ve y =
2x − 1
=
−
x −1
2
doğrularının kesişme noktası doğrunun parabole
Buna dik olan doğru için eğim = −
x2 − x − 13 =
0
bu apsislerin toplamı ,
−1
−
=
x1 + x 2 =
1 elde edilir.
1
y
f(x)
en yakın noktası olup =
y 2x − 1 diğer denklemde
yazılırsa
y−7
1
2x − 1 − 7
1
17
= − ⇒
=
− ⇒x=
elde edilir.
x −1
2
x −1
2
5
B
O
A
2
7
18.
x
y =+
mx 2 ve y =
2x 2
y
A ve B noktaları için
g(x)
y=2x 2
2
=
2x
mx + 2
2x2 − mx − 2 =
0
Parabolün denklemi ,
y = a • (x − 2) • (x − 7)
denklemine bakılır.
Orta noktaların apsisi
−m
b
−
=
−
r=
2a
2•2
m
x=
ve ordinatı
4
2
⇒ y = ax − 9ax + 14a olur.
Doğrunun denklemi ,
⇒ y = kx (orijinden geçen doğru denklemi)
Parabol ile doğrunun kesiştiği noktaları veren
denklem ,
A
g(x)
B
2
O
m
m2
+ 2 ⇒ y = + 2 dir.
4
4
m
m2
x
m 4x=
y
=
+ 2 yerine yazılırsa
⇒=
4
4
orta noktalarının geometrik yer denklemi
⇒y=
mx + 2 ⇒ y =
m•
ax2 − 9ax + 14a =
kx
ax2 − (9a + k)x + 14a =
0
bu apsislerin çarpımı ,
c 14a
=
= 14 elde edilir.
x1 • x=
2
a
a
www.yukseklimit.com
y=
2x − 1 ve y =
x2 + 6
Önce parabolün doğruya en yakın noktasını
bulalım. Parabolün doğruya en yakın olduğu
Parametrik denklemleri,
=
x 2t + 1
15.
y=
− x 2 + 8 ve y =
2x + 11
Parabolün doğruya en yakın olduğu noktanın
m2
(4x)2
y= +2⇒y=
+ 2⇒ y =
4x2 + 2 olur.
4
4
33
Mehmet Ali AYDIN
x
6−II. DERECEDEN FONKSÝYONLAR−2(Parabol) (Grafikten Parabolün Denklemi-Parabol ve Doðru) LYS MATEMATÝK
19.
=
x y2 − 4y + 3
y 0=
için x 3 olup Ox
=
22.
y
3
eksenini (3,0) da keser.
y = ax 2 + bx + c
olsun. Parabolün geçtiği yukarıdaki noktalar
parabolün denklemini sağlayacağından
2
x = 0 için 0 = y2 − 4y + 3
1
x
(y − 3) • (y − 1)= 0 y= 3
−1 O 3
veya y = 1 olup Oy
eksenini kestiği noktalar
A(0,3) ve B(0,1) dir. Tepe noktası T(−1,2) dir.
20.
A(−1,7) ⇒ 7 =
a • (−1)2 + b • (−1) + c ⇒ a − b + c =
7
B(1,5) ⇒ =
5 a • 12 + b • 1 + c ⇒ a + b + =
c 5
C(2,7) ⇒=
7 a • 22 + b • 2 + c ⇒ 4a + 2b +=
c 7
Böylece ,
a−b+c =
7
a + b + c =5 a =
1 , b =−1 , c =5 tir.
4a + 2b + c =
7
x = y2
− 32y =
x3
O halde , y = x 2 − x + 5 elde edilir.
Bu eğrilerin kesişme noktaları için x = y2
diğer denklemde yazılırsa ,
23.
3
x
− 32y =
3
(y )
⇒ −32y =
2
y
=
y x 2 − 4x parabolünün
grafiği çizilir ve
y=x
y ≥ x 2 − 4x için parabol
6
⇒ −32y =
y
ve üst bölgesi taranır.
⇒ y6 + 32y =
0
=
x 0 için =
y x 2 − 4x
O
x
4
⇒ y • (y5 + 32) =
0
Buradan y = 0 veya y = −2 kesişim noktala rının ordinatlarıdır.
⇒ y =02 − 4 • 0 =0 olur.
Parabolün y eksenini kestiği nokta A(0,0) dır.
Bu değerler denklemlerden birinde örneğin
=
x 0=
ve x 4 tür.
Parabolün x eksenini kestiği noktalar B(0,0)
y=
0 için y =
x 2 − 4x ⇒ 0 =
x 2 − 4x
=
⇒ 0 x • (x − 4)
x = y2 ifadesinde yazılırsa
=
y 0=
için x y2
ve C(4,0) dır.
Parabolün Tepe noktası T(2, −4) tür.
2
=
⇒ x 0=
⇒x 0
−2 için x =
y=
y2
y − x < 0 ⇒ y < x için y =
x doğrusunun grafiği
çizilir ve doğru alınmayıp alt bölgesi taranır.
(−2)2 ⇒ x =
4 elde edilir.
⇒x=
O halde kesişme noktaları A(0,0) ve B(4, −2)
elde edilir.
Böylece ortak bölgenin grafiği elde edilir.
24.
21.
A(−1,7) , B(1,5) ve C(2,7) noktalarından geçen
parabolün denklemi ,
b
6
⇒r =
−
=
3
2a
2 • (−1)
A nın en büyük değeri için a yerine 3 yazılır sa
AB = 4 br olduğundan
− a 2 + 6a + 1 ⇒ r =
−
A=
x1= n ve x2= n + 4
2
O
n
A
− x + 8x + a
y=
b
−
x1 + x 2 =
a
8
⇒ n + n + 4 =−
2 • (−1)
⇒ 2n +=
4 8 ⇒=
n 2 tür.
=
O halde kökler
x1 2=
ve x 2 6 dır.
A=
− a2 + 6a + 1
⇒ A =−32 + 6 • 3 + 1 =10 elde edilir.
⇒ A = 10 elde edilir.
4
4
2
B=
2b + 4b − 41 ⇒ r =
⇒r =
−
−
=
−1
2a
2•2
B nin en küçük değeri için b yerine − 1 yazı -
=
x1 • x 2
lırsa
c
⇒2•6
=
a
n+4
B
x
f(x)
a
⇒ a −12 elde edilir.
=
−1
Böylece f(x) =
− x 2 + 8x − 12 elde edilir.
f(x) in alabileceği en büyük değer f(r) dir.
b
8
r=
4 tür.
−
⇒r =
−
⇒r =
2a
2 • (−1)
B = 2b2 + 4b − 41
⇒ B = 2(−1)2 + 4 • (−1) − 41
⇒ B = −43 elde edilir.
−42 + 8 • 4 − 12 =
f(r) =
f(4) =
4 elde edilir.
Yani f(x) ≤ 4 olacağından f(x) → 0, 1, 2, 3, 4
olmak üzere 5 farklı doğal sayı değeri alabilir.
−33 elde edilir.
Böylece A + B =
www.yukseklimit.com
y
Grafikte A ve B kökleri
ifade ettiğinden ve
34
Mehmet Ali AYDIN
6−II. DERECEDEN FONKSÝYONLAR−2(Parabol) (Grafikten Parabolün Denklemi-Parabol ve Doðru) LYS MATEMATÝK
25.
28.
f(x) parabolü Ox eksenini − 2 ve 5 apsisli
noktalarda kestiğine göre,
f(x)
= a • (x − (−2)) • (x − 5)
f(x) = a • (x + 2) • (x − 5) elde edilir.
O halde ,
f(x) = x 2 + 5x − 2
x2 + 5x − 2= 2x 2 + 5x − 3
x2 = −1 elde edilir.
Böylece sabit noktaların apsisleri
x = 1 ve x = −1 elde edilir.
Ordinatlar için
y = f(x) = x2 + 5x − 2
y=
mx 2 + 4x + 2 ve y =
−2
parabol ile doğrunun teğet olması için ,
mx2 + 4x + 2 =−2
mx2 + 4x + 4 =
0
denklemi için ∆ =0 olmalıdır.
=
∆ b2 − 4 • a • c
y = f(x) = 2x 2 + 5x − 3
denklemlerinden birinde
x 1=
yazılırsa y 4
=
x=
−1 yazılırsa y =
−6 elde edilir.
Böylece , sabit noktalar (1, 4) ve (−1, −6) dır.
(x 1, y1 ) ve (x 2 , y2 ) den geçen doğru denklemi
∆= 42 − 4 • m • 4 ⇒ 0= 16 − 16m ⇒ m= 1 dir.
m = 1 denklemde yazılırsa
y − y1
y − y1
= 2
dir.
x − x1
x2 − x1
mx 2 + 4x + 2 =−2
(1,4) ve (−1, −6) dan geçen doğru denklemi
x 2 + 4x + 4 =
0
(x + 2) • (x + 2) =
0
Buradan x = −2 teğet noktanın apsisidir.
Teğet noktanın ordinatı için
y = x2 + 4x + 2
y = −2
y−4
−6 − 4
dir.
=
x −1
−1 − 1
y 5x − 1) elde edilir.
=
(m = 1 alındı)
29.
denklemlerinden birinde x = −2 yazılırsa
y =−2 elde edilir. Yani teğet nokta A(−2, −2)
dir ve K(a,b) noktasının orijine olan uzaklığı
27.
=
∆ b2 − 4 • a • c
1 m2 − 4 • 1 • 6
−=
m2 = 23 elde edilir.
(−2)2 + (−2)2 ⇒ 2 2 br elde edilir.
O halde m nin pozitif değeri
y2 =2x eğrisi ile y =− x + 4 doğrusunun kesiş tiği A ve B noktalarının apsislerini veren denk -
30.
lem için y2 =2x ifadesinde y =− x + 4 yazılırsa
2
y = 2x
23
2
x − 8x + 16 =
2x
x2 − 10x + 16 =
0
y = f(x) = x 2 − 2x + 4
Orijinden geçen
teğet olduğuna göre ,
(x − 2) • (x − 8) = 0
=
Buradan
x 2=
ve x 8 apsisleri elde edilir.
Ordinatlar için
x 2 − 2x + 4 =
mx
elde edilir.
y
Parabolün denklemi
f(x)
doğrunun denklemi
=
= mx tir.
y g(x)
Doğru ile parabol
(− x + 4)2 =
2x
g(x)
A
O
x
x2 − (2 + m)x + 4 =
0
denklemi için ∆ =0 dır.
y2 = 2x
y =− x + 4
denklemlerinden birinde örneğin y =− x + 4 te
∆= (2 + m)2 − 4 • 1 • 4 ⇒ (2 + m)2 = 16 dır.
−4 olacağından
2+m=
4 veya 2 + m =
m = 2 veya m = −6 elde edilir.
x 2=
yazılırsa y 2
=
x = 6 yazılırsa y = −2 elde edilir.
O halde , A(2,2) ve A(6, −2) elde edilir.
Bütün koordinatlar toplanırsa
⇒ 2 + 2 + 6 + (−2)
⇒ 8 elde edilir.
www.yukseklimit.com
y =x2 + mx + 6
parabolüne orijinden çizilen teğetler dik ke sişiyorsa ∆ = −1 dir.(
a2 + b2 olduğundan bu noktanın orijine olan
uzaklığ
(a = 5 için)
f(x) = 2x 2 + 5x − 3
(a = 6 için)
parabollerinin geçtiği sabit noktalar bu
parabollerin kesişim noktalarıdır. O halde ,
f(10) a • (10 + 2) • (10 − 5)
=
f(4)
a • (4 + 2) • (4 − 5)
f(10)
a • 12 • 5
=
f(4)
a • 6 • (−1)
f(10)
= −10 elde edilir.
f(4)
26.
f(x) = (a − 4)x2 + 5x + 3 − a
Rastgele
a 5=
ve a 6 alınırsa
=
=
m 2 için
=
+4 0
x 2 − (2 + m)x
2
x − 4x + 4 =
0
(x − 2) • (x =
− 2) 0 ve
=
x 2 elde edilir.
m=
−6 için x =
−2 olduğundan imkansızdır.
35
Mehmet Ali AYDIN
6−II. DERECEDEN FONKSÝYONLAR−2(Parabol) (Grafikten Parabolün Denklemi-Parabol ve Doðru) LYS MATEMATÝK
31.
Yanda grafiği verilen
3 2
f(x)=
x − 3x + k
4
parabolünün tepe
noktası T(r,n) ise
y
Şekle göre m = −2 dir. O halde ,
f(x)
x 2 − (2 + m)x − 3 =
0
x 2 − 3 =0 dan x = 3 ya da x =− 3
−2x te
Bu apsisler y =
x2 − 2x − 3 ya da y =
O 2 4
b
x
−
⇒r =
r=
2
2a
=
⇒ f(2) n ⇒
f(r) n=
−3
A
f(2) =
k−3⇒n=
k−3
tür. f(0) = k değeri
−6
T
C nin ordinatı olup
=
=
n 2k
dır. O halde , n k − 3 yerine yazılırsa
⇒ 2k =
k−3⇒k =
−3 tür ve
3 2
f(x)=
x − 3x − 3 elde edilir.
4
A nın apsisi f(x) = −3 denkleminin köklerinden
pozitif olanıdır.
3 2
x − 3x − 3 =−3 ten x =0 ya da x =4 tür.
4
Yani A nın apsisi 4 tür. O halde , eşkenar
e•f
4•6
dörtgenin alanı = = 24 br 2 elde edilir.
2
2
32.
34.
10
35.
36.
f(x)
2
x − 2x − 3 =
m
2
x − (2 + m)x − 3 =
0
A(x1, y1) ve B(x 2 , y2 )
noktaları orijine göre
simetrik olduğundan
A ve B nin ortası (0,0)
dır. Yani
x1 + x 2
= 0 ve
2
x1
−1
y2
O x2
3
x
y = x 2 − 4x − 12
parabolünün grafiği
ve y = −6 doğrusuna
göre simetriğinin gra fiği çizilmiştir.
Yeni parabol orijinden
geçer ve Tepe
noktası T(2, 4) olur.
Tepe noktası T(r,k) olan
parabolün denklemi ,
f(x)= a • (x − r)2 + k
−3
α
x
B
y
−2
4
O
f(x)
2
−6
6
x
y= −6
−12
−16
olduğundan
2
f(x) = a • (x − 2) + 4
B
elde edilir.
f(0) = 0 olduğundan
y=−2x
y1 + y2
− (2 + m)
=
0 elde edilir. x1 + x2 =
−
=
2+m
2
1
y1 + y2= m • (x1 + x2 ) ⇒ y1 + y2= m • (2 + m)
−2 dir.
0=
m • (2 + m) ve m =
0 ya da m =
www.yukseklimit.com
A
denkleminin pozitif kökü olan 3 tür.
6
= −2 3 tür.
O halde tanα = − tanβ = −
3
y1
A
β
− 2x2 + 12 = 6
f(a) =
f(−8) =
−(−8)2 + 4(−8) − 8 ⇒ f(−8) =
−104 tür.
Orijinden geçen
doğru y = mx tir.
A ve B nin apsis lerininin denklemi
6
g(x)
f(x)
−2x2 + 12 dir.
f(x) =
T nin ordinatı f(0) = 12 olduğundan A nın or dinatı benzerlikten dolayı 6 dır.
A nın apsisi
f(x) =
− x 2 + 4x − 8 ⇒
y
12
f(x) = mx 2 + (m2 − 4)x − 6m
16 ve a =
0 dır.
⇒ (4 + a)2 =
−8 ya da a =
Şekilde a = −8 olduğu görülür. O halde ,
f(x) = x2 − 2x − 3 ve
y
2
=
− 4 0 dan
=
m
m 2 ya
da m = −2 elde edilir.
Kollar aşağı olduğundan
m = −2 dir. O halde ,
geçen [OT] nin eğimi
T
4+a−0
4+a
m1 =
=
2−0
2
T(2,4 + a) ve (10,0) dan
f(x)
geçen doğrunun eğimi
0 − (4 + a)
−4 − a
m2 =
=
Diklikten m1 • m2 = −1
10 − 2
8
4 + a −4 − a
•
⇒
=
−1 ve a =
−4 elde edilir.
8
2
33.
Tepe noktası Oy üzerin de olduğundan
f(x) = mx 2 + (m2 − 4)x − 6m
x
O
f(x) = ax 2 + bx + c
a • f(k ) < 0 ise k köklerin arasındadır.
f(−3 )= f(5 )= 0
olduğundan kökler − 3 ve 5 tir.
O halde a • f(α ) ≤ 0 olduğundan
−3≤α≤5
α nın alabileceği değerlerin toplamı,
⇒ (−3) + (−2) + (−1) + 0 + 1 + 2 + 3 + 4 + 5
⇒ 9 elde edilir.
y
2
f(x) =
− x + 4x + a
Tepe noktası T(2,4 + a)
T(2,4 + a) ve orijinden
yazılırsa ordinatlar y =
2 3 tür.
−2 3 ya da y =
Böylece ordinatlar arası uzaklık 4 3 elde edilir.
f(0) = a • (0 − 2)2 + 4
−1 olur
0=
4a + 4 ⇒ a =
ve yukarıda yazılırsa
2
f(x) =
− (x − 2) + 4
− x 2 + 4x elde edilir.
f(x) =
36
Mehmet Ali AYDIN
7−UZAYDA DOÐRU ve DÜZLEM ANALÝTÝÐÝ
1.
2.
LYS GEOMETRÝ
A(−1,4,9) ile B(2,0,c) noktaları arası uzaklık
13 birim olduğuna göre, c nin alabileceği
değerlerin toplamı kaçtır?(18)
Á
4.
A(2, −3,1) noktasından geçen ve d =
( −2,1,3)
vektörüne paralel olan doğrunun kartezyen
x−2
z −1
= y+3=
denklemi nedir?(
)
3
−2
5.
A(3, −2,6) noktasından geçen ve d =
(0,2, −2)
vektörüne paralel olan doğrunun kartezyen
denklemi nedir?
x−3
y+2
z−6
y+2
z−6
(= =
) veya
=
(x 3, =
)
0
2
−2
2
−2
x2 + y2 + z 2 + 6x + 4y − 2z =
−3
denklemi ile tanımlanan kürenin,
a) Merkezinin koordinatları nedir?((−3, −2,1))
Á
b) Yarıçapı kaç birimdir?( 11)
3.
Á
A(2, −3,1) noktasından geçen ve d =
(−2,1,3)
x+2
z−1
6.
A = (12,k, −8) vektörü
= y−3=
vektörüne paralel olan doğrunun parametrik
3
−2
doğrusuna paralel olduğuna göre, k kaç
denklemi nedir?
tır?(4)
x= 2 − 2k
y =−3 + k
z= 1 + 3k
www.yukseklimit.com
Á
219
Mehmet Ali AYDIN
7−UZAYDA DOÐRU ve DÜZLEM ANALÝTÝÐÝ
7.
LYS GEOMETRÝ
10.
A(1,2, −2) ve B(2,3,0) noktalarından geçen
doğrunun denklemi nedir?
x −1 y−2
z+2
x−2
(= =
) veya ( =
1
1
2
1
y−3
=
1
z
)
2
x+3
y−1 z+ 3
= =
1
1
2
x −1 y+1
z
= =
−2
2
−2 2
doğruları arasındaki açı kaç derece dir?(60 veya 120)
8.
x+4
y−1
= =
−3
a
x+1 y+2
= =
−2
6
11.
z
4
z+a
b
x−2
y+3
z
=
=
−1
2
1
11
doğrusuna olan uzaklığı kaç birimdir?(
)
6
P(−1,0,2) noktasının,
doğruları paralel olduğuna göre, a + b top lamı kaçtır?(−7)
9.
12.
Denklemi,
x
y
z
= =
−4
a
2
x+1 y−2
d2 : = =
−2
3
Á
A(2, −1,0) noktasından geçen ve N =
(3,1, −1)
vektörüne dik olan düzlemin denklemi ne dir?(3x + y − z − 5 =
0)
d1 :
z−4
−1
olan doğruların birbirine dik durumlu olması
için, a kaç olmalıdır?(5)
www.yukseklimit.com
220
Mehmet Ali AYDIN
7−UZAYDA DOÐRU ve DÜZLEM ANALÝTÝÐÝ
13.
x+
2y − z + 5 =
0
x−
2y + z − 1=
0
LYS GEOMETRÝ
16.
2x + y + z − 1=
0
düzlemi ile
düzlemleri arasındaki açı kaç derecedir?
x−2
=
2
(60 veya 120)
y+3
=
−1
z−4
1
doğrusu arasındaki açı kaç derece dir?(30 veya 150)
14.
17.
x − 2y + kz − 4 =
0
2x + 3y − z + 1 =
0
x
=
−3
y+1
=
2
z−2
a
doğrusu,
düzlemleri dik olduğuna göre, k kaçtır?(−4)
bx + 4y − 2z + 3 =
0
düzlemine dik olduğuna göre, a ve b kaç
olmalıdır?(a =
−1, b =
−6)
15.
18.
x=
− ky − 3z 7 düzlemi, − x =
+ 2y + 3z 6 düz lemine paralel olduğuna göre, k kaçtır?(2)
x+1
=
2
y
=
a
z−5
4
doğrusu,
3x − y + 2z − 2 =
0
düzlemine paralel olduğuna göre, a kaç tır?(14)
www.yukseklimit.com
221
Mehmet Ali AYDIN
7−UZAYDA DOÐRU ve DÜZLEM ANALÝTÝÐÝ
19.
x+1
=
1
y+3
=
2
LYS GEOMETRÝ
22.
z−3
−2
doğrusunun,
A) 3x + 6y − 5z + 13 =
0
B) x − 2y + 3z − 5 =
0
C) 2x + z + 7 =
0
D) 2x − y + 4 =
0
E) x − 2y − 9 =
0
− x − 3y + 2z + 6 =
0
düzlemini kestiği nokta nedir?((1,1, −1))
20.
Parametrik koordinatları P(2k − 1,5 − k,7)
olan doğru aşağıdaki düzlemlerden han gisine paraleldir?
x− y+z−6=
0
0
−x+y−z+3=
23.
3x − 2y + z − 5 =
0
2x + y − z + 3 =
0
düzlemlerinin arakesit doğrusunun doğrult -
düzlemleri arası uzaklık kaç birimdir?( 3 )
man vektörü nedir?((1,5,7))
21.
24.
A(−1, 4,3) noktasından geçen ve 3x − 2y + z =
3
düzlemine paralel olan
nedir?(3x − 2y + z + 8 =
0)
düzlemin denklemi
= [2,0, −2]
Á Alemine
dik
vektörünün 3x − 3y + 7
= 0 düz izdüşümünün uzunluğu kaç bi -
rimdir?( 6 )
TEST − 7 CEVAPLAR :
www.yukseklimit.com
222
22) D
Mehmet Ali AYDIN
DENEME−1
MATEMATÝK−GEOMETRÝ DENEMELERÝ
o
1.
=
x 75
=
ve y 45
o
4.
olduğuna göre,
sin(x − y)cos(x + y) + sin(x + y)cos(x − y)
sin(x − y)sin(x + y) − cos(x + y)cos(x − y)
denkleminin kaç tane farklı reel kökü vardır?
ifadesinin eşiti kaçtır?
A) − 3
2.
B) −
1
3
C)
A) 0
2 −1
π
π
tan 8 − cot 8
1
3
D)
E)
3.
B) 2
5.
2
C) 3
D) 4
•
1
10
6.
E) 4
D) 3
E) e3
3
B)
1
3
C)
3
x+3
4 −
1+ x
x
1+ x
+
:
1− x 1+ x
ifadesinin sadeleştirilmiş biçimi aşağıdakilerden
hangisidir?
Buna göre, (1 + 2i) • (1 + 3i) işleminin sonucu a şağıdakilerden hangisidir?
www.yukseklimit.com
D) 3
işlemi,
biçiminde tanımlanmıştır.
C) 1
( 0,1)logx = e2ln
A)
E) 6
arctan(z1 =
• z2 ) arg(z1 ⋅ z2 )
B) 0
C) 2
denklemine göre, x kaçtır?
Karmaşık sayılar kümesi üzerinde
A) − 1
B) 1
3
ifadesinin eşiti kaçtır?
A) 1
x3 − x 2 + 8 =
0
A) x − 1
π
D)
4
7π
E)
4
229
B) 1 − x
C)
1
1− x
D)
1
1+ x
E) 1
Mehmet Ali AYDIN
DENEME−1
MATEMATÝK−GEOMETRÝ DENEMELERÝ
7.
10.
1
1
x+ 2
x +
x =
2
1
1
x− 2
x2 +
x
x
x2 −
denkleminin çözüm kümesi
fonksiyonunun tanım kümesi R olduğuna göre,
aşağıdakilerden
A) − 1
D) { 2, 3 }
B) { − 1, 1 } C) {0, 2 }
B) 0
D) 1,5
C) 1
E) 2
E) { }
11.
8.
x2 + x
x + mx + 1
2
m aşağıdakilerden hangisi olamaz?
hangisidir?
A) { − 1 }
f(x) =
1 −
lim
x →∞
1 −
1 1
y = x 3 eğrisine A , noktasından çizilen te 2 8
ğet doğrusu üzerinde farklı bir B noktası alınıyor.
A ve B noktalarının apsisleri arası uzaklık 2 bi -
3
1
− 1+
x
2
1
− 1+
x
1
x
1
x
3
2
limitinin değeri kaçtır?
rim olduğuna göre, AB kaç birim dir?
A) 1,5
9.
=
( an )
B) 2
1
+
2 +1
C) 2,4
D) 2,5
1
+ ⋅⋅⋅+
3 + 2
1
n+1 +
A) 3
E) 3,2
12.
n
B) 2
C)
3
2
D) 1
E)
2
3
f(x)
= x 4 − 8x 2
fonksiyonunun (− 13 , 13 ) aralığında alabile ceği en büyük tam sayı değeri kaçtır?
dizisinin kaçıncı terimi 10 dur?
A) 120
B) 121
www.yukseklimit.com
C) 143
D) 144
E) 168
A) 8
230
B) 9
C) 32
D) 64
E) 65
Mehmet Ali AYDIN
DENEME−1
13.
MATEMATÝK−GEOMETRÝ DENEMELERÝ
16.
P(x) polinomunun katsayılarının toplamı 1, P(x) in
türevinin katsayılarının toplamı ise 4 tür.
y
f(x)=x
Buna göre, P(P(x)) polinomunun türevinin x−1
ile bölümünden kalan kaçtır?
A) 1
B) 2
C) 4
D) 8
E) 16
D
C
A
B
2
x
O
g(x)=12−x 2
Yukarıdaki şekilde aynı ordinatlı C ve D noktaları
g(x) parabolü üzerinde, A ve B noktaları ise f(x)
parabolü üzerindedir.
Buna göre, oluşturulabilecek ABCD dikdörtgen -
14.
lerinden alanı en büyük olanın alanı kaç birim
x3 = y 2
karedir?
y3 = x 2
A) 32
eğrileriyle sınırlı olan bölgenin alanı kaç birim
B) 24
C) 16 2
D) 16
E)9
karedir?
A)
1
6
B)
1
5
C)
1
4
D)
1
3
E)
1
2
17.
π
∫ ( tan(π + x) + sin(π − x)) dx
0
15.
2
∫
1
3π
integralinde x + y = dönüşümü yapılırsa a 2
şağıdaki integrallerden hangisi elde edilir?
x2 + x + 1
dx
x
0
A)
integralinin değeri kaçtır?
∫
3π / 2
( tan y + cos y ) dy
B)
3π / 2
A)
5
+ ln2
2
B)
D)
www.yukseklimit.com
3
+ ln 2
8
7ln 2
8
C)
C) 7 − ln 2
∫
∫ ( tan y − cos y ) dy
π/2
π
3π / 2
( cos y − cot y ) dy
π/2
D)
∫ (cot y − cos y ) dy
π/2
π/2
E)
E) ln 2
∫ (cos y − cot y ) dy
0
231
Mehmet Ali AYDIN
DENEME−1
18.
MATEMATÝK−GEOMETRÝ DENEMELERÝ
20.
P(x) bir polinomdur.
P '(x) +
x −x
∫ P(x)dx =
2
D
olduğuna göre, P(2) kaçtır?
A) 0
B) 1
C) 2
C
7
D) 3
9
x
7
E) 4
A
B
14
ABCD konveks dörtgen, =
DC
=
AD 7 cm
=
AB 14=
cm, BC 9=
cm, AC x cm olduğuna
göre, x in alabileceği kaç farklı tam sayı de ğeri vardır?
A) 5
19.
B) 6
C) 7
D) 8
E) 9
A
a
B
b
h
p
D
C
k
ABC üçgen, [AD] ^ [BC],
AD = h cm
21.
=
BD p=
cm, DC k=
cm, AB a cm
AC = b cm dir.
AC kenarını D noktasında kesmektedir.
a2 × b 2
a 2 + b2
eşiti aşağıdakilerden hangisidir?
h2 = p × k olduğuna göre,
A) a
B) b
www.yukseklimit.com
ABC dik üçgeni için AC = 10 cm olarak verilmiş tir. Merkezi C ve yarıçapı [BC] olan bir çember
C) h
D) p
AD = 2 cm olduğuna göre, Alan(ABC) kaç cm2
ifadesinin
dir?
A) 12
E) k
232
B) 16
C) 18
D) 24
E) 32
Mehmet Ali AYDIN
DENEME−1
MATEMATÝK−GEOMETRÝ DENEMELERÝ
22.
24.
C
D
8
C
E
10
D
4
H
E
F
G
G
A
A
B
22
B
F
ABCD yamuk, [AB] // [FG] // [EH] // [DC]
ABC üçgen, G ağırlık
=
=
AB 22
cm, DC 8 cm olduğuna göre,
merkezi
[CF] ∩ [AE] ∩ [BD] = {G},
EH + FG
AF = FB = GF
=
=
GC 10
cm, DG 4 cm olduğuna göre,
A) 24
Alan(DGC) kaç cm2 dir?
A) 16
B) 12
C) 8
D) 6
toplamı kaç cm dir?
B) 26
C) 28
D) 30
E) 3
25.
C
D
x
E
23.
D
E) 32
4
C
A
4
4
F
L
B
K
F
G
15
A
B
B noktasında teğet olan [LB] ve [AB] çaplı çem -
E
berlerin merkezleri sırasıyla K ve L dir.
ABCD dikdörtgen, [CE] ⊥ [AF], A,B,E doğrusal
CG
=
[CB] çemberlere B noktasında, [CF] ise küçük
GB , CF 4=
cm, AG 15 cm olduğuna
=
=
çembere E noktasında teğet, AF
göre, Alan(AGCD) kaç cm2 dir?
A) 90
B) 72
www.yukseklimit.com
C) 64
D) 60
FE
= 4 cm
BC = x cm olduğuna göre, x kaçtır?
E) 54
A) 6
233
B) 2 10
C) 4 3
D) 7
E) 5 2
Mehmet Ali AYDIN
DENEME−1
26.
MATEMATÝK−GEOMETRÝ DENEMELERÝ
D
28.
C
H
ÁV
1
Á
( 4, 1 − a ) ve V2 =
( − 3, a + 1) vektörleri doğ =
rusal bağımlı olduğuna göre, a kaçtır?
A) − 7
E
G
K
C)
1
7
D) 1
E) 7
B
F
29.
Yukarıdaki şekildeki çember, alanı 16 cm2 olan
ABCD karesinin kenarlarına E, F, G ve H nok talarında teğet ve KL = 2 2 cm olduğuna göre,
taralı bölgelerin alanlarının toplamı kaç cm2 dir?
B) p +
1
7
L
2
A
A) p + 2
B) −
2
C) p
D) 2 +
2
x
+ 8 ve
4
x = 0 doğrularının oluşturduğu üçgenin çevrel
çemberinin denklemi aşağıdakilerden hangisi dir?
Analitik düzlemde, y =
4x + 16, y =
−
A) x 2 + (y − 12)2 =
16
E) 2
B) (x − 12)2 + y 2 =
16
C) (x − 8)2 + (y − 6)2 =
36
D) x 2 + y 2 =
16
E) x 2 + y 2 =
64
27.
D
30.
C
y
K
2
A
F
1
O
A
A
F
O
x
B
Tabanlarının çevresi küreye içten teğet olan yu karıdaki şekildeki dik silindirin taban yarıçapı 1 cm
Yukarıdaki şekilde verilen elipsin denklemi
ve yüksekliği 2 2 cm olduğuna göre, kürenin
x2
y2
1 ve odakları F ' , F dir.
+
=
100 64
3
hacmi kaç cm tür.
A) 4p
B) 4 2 p
C) 6p
D) 4 3 p
E) 5 2 p
[F'F] çaplı çemberin K noktasındaki teğeti A'
köşesinden geçtiğine göre, K nın ordinatı kaç tır?
A) 2,4
B) 3,6
DENEME-1 : 1-D
2-D
3-A
4-B
5-B
6-B
7-E
8-D
9-A
10-E
16-C
17-D
18-D
19-C
20-D
21-D
22-B
23-A
24-D
25-A
www.yukseklimit.com
234
C) 4,2
D) 4, 8
E) 5,6
11-C 12-D 13-E 14-B 15-A
26-E
27-D
28-A
29-A
30-D
Mehmet Ali AYDIN