İNTEGRAL 6
BELİRLİ İNTEGRAL
[ a , b ]⊂ℝ ARALIĞININ PARÇALANIŞI VE
RİEMANN TOPLAMI
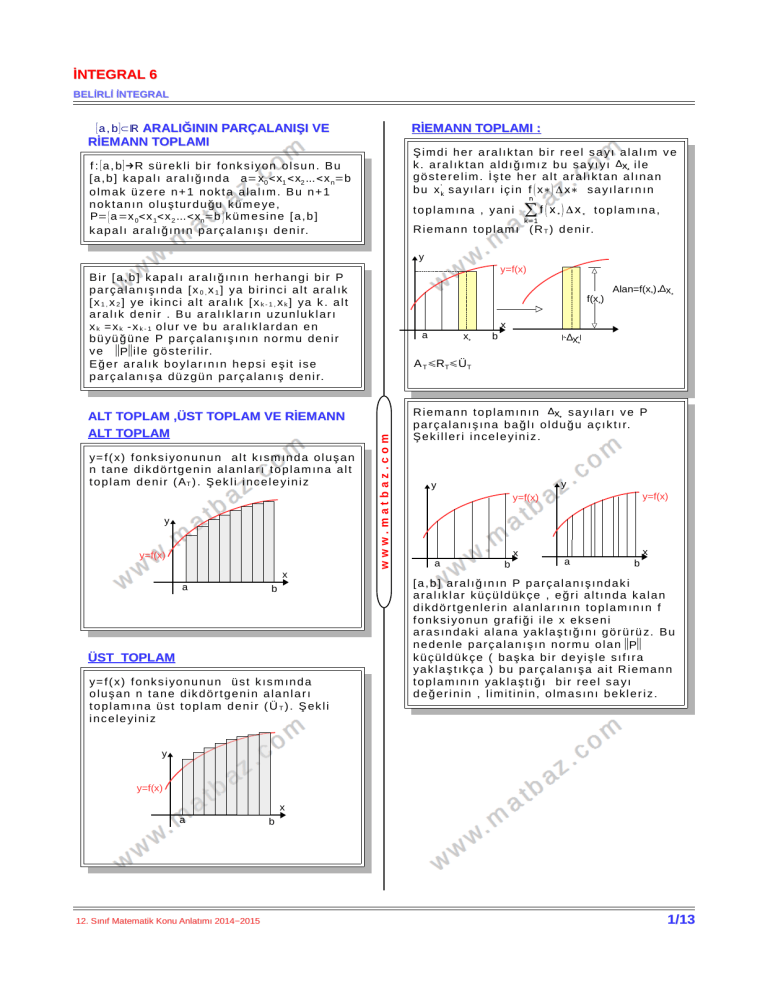
RİEMANN TOPLAMI :
Ş i m d i h e r a r a l ık t a n b i r r e e l s a yı a l a l ım v e
k . a r a l ık t a n a l d ığ ım ı z b u s a yı yı
ile
g ö s t e r e l i m . İ ş t e h e r a l t a r a l ık t a n a l ın a n
b u x 'k s a yı l a r ı i ç i n f ( x∗) Δ x∗ s a yı l a r ı n ın
f : [ a , b ] →R s ü r e k l i b i r f o nk s i yo n o l s u n . B u
[ a , b ] k a p a l ı a r a l ı ğ ı n d a a= x0 <x1 <x2 ...<x n=b
o lm ak ü z e r e n + 1 n ok t a a l a l ım . B u n + 1
n ok t a n ı n o l u ş t u r d u ğ u k üm e ye ,
P= {a =x 0<x 1<x 2 ...<xn=b } k üm e s i n e [ a , b ]
k a p a l ı a r a l ı ğ ı n ı n p a r ç a l a n ı ş ı d e n i r.
t o p l a m ın a , ya n i
t o p l am ın a ,
R i e m a n n t o p l am ı ( R T ) d e n i r.
y
y=f(x)
Bir [a,b] kapalı aralığının herhangi bir P
p a r ç a l a n ı ş ı n d a [ x 0 , x 1 ] ya b i r i n c i a l t a r a l ık
[ x 1 , x 2 ] ye i k i n c i a l t a r a l ı k [ x k - 1 , x k ] ya k . a l t
a r a l ı k d e n i r . B u a r a l ık l a r ı n u zu n l u k l a r ı
xk =xk -xk-1 olur ve bu aralıklardan en
b ü yü ğ ü n e P p a r ç a l a n ı ş ı n ı n n o r m u d e n i r
v e ∥P∥i l e g ö s t e r i l i r.
E ğ e r a r a l ı k b o yl a r ı n ı n h e p s i e ş i t i s e
p a r ç a l a n ı ş a d ü zg ü n p a r ç a l a n ı ş d e n i r.
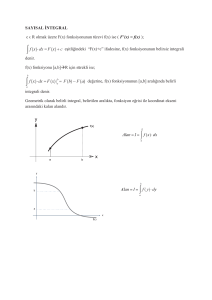
y= f ( x ) f o nk s i yo n u n u n a l t k ı s m ı n d a o l u ş a n
n tane dikdörtgenin alanları toplamına alt
t o p l am d e n i r ( A T ) . Ş ek l i i n c e l e yi n i z
y
y=f(x)
x
a
b
ÜST TOPLAM
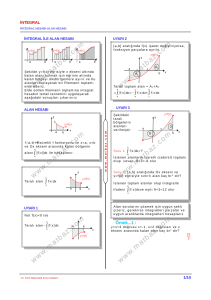
y= f ( x ) f o nk s i yo n u n u n ü s t k ı s m ı n d a
oluşan n tane dikdörtgenin alanları
t o p l am ı n a ü s t t o p l a m d e n i r ( Ü T ) . Ş ek l i
i n c e l e yi n i z
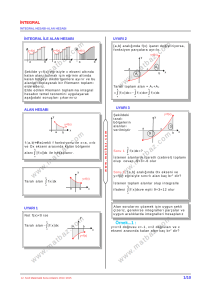
Alan=f(x*).∆x*
x
a
x*
b
∆x
*
A T ⩽RT⩽ÜT
www.matbaz.com
ALT TOPLAM ,ÜST TOPLAM VE RİEMANN
ALT TOPLAM
f(x*)
R i e m a n n t o p l am ın ın
s a yı l a r ı v e P
p a r ç a l a n ış ın a b a ğ l ı o l d u ğ u a ç ık t ır.
Ş e k i l l e r i i n c e l e yi n i z.
y
y
y=f(x)
y=f(x)
a
x
b
a
x
b
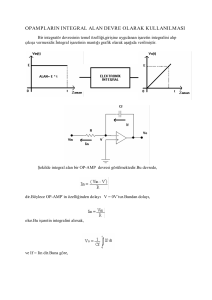
[ a , b ] a r a l ığ ın ın P p a r ç a l a n ış ın d a k i
a r a l ık l a r k ü ç ü l d ük ç e , e ğ r i a l t ın d a k a l a n
d i k d ö r t g e n l e r i n a l a n l a r ı n ı n t o p l a m ın ın f
f on k s i yo n u n g r af i ğ i i l e x e k s e n i
a r a s ın d a k i a l a n a ya k l a ş t ığ ı n ı g ö r ü r ü z. B u
n e d e n l e p a r ç a l a n ı ş ı n n o r m u o l a n ∥P∥
k üç ü l d ü k ç e ( b a şk a b i r d e yi ş l e s ıf ır a
ya k l a ş t ık ç a ) b u p a r ç a l a n ı ş a a i t R i e m a n n
t o p l a m ın ın ya k l a ş t ığ ı b i r r e e l s a yı
d e ğ e r i n i n , l im i t i n i n , o lm a s ın ı b e k l e r i z.
y
y=f(x)
x
a
12. Sınıf Matematik Konu Anlatımı 2014−2015
b
1/13
İNTEGRAL 6
BELİRLİ İNTEGRAL
RİEMANN TOPLAMI OLARAK BELİRLİ
İNTEGRALİ
Al t t o p l a m
y=x+2
f : [ a , b ] →R b i r f o nk s i yo n o l s u n . P [ a , b ]
a r a l ı ğ ı n ı n h e r h a n g i b i r p a r ç a l a n ı ş ı v e x 'k
bu parçalanışa ait [xk-1,xk] aralığından
s e ç i l e n h e r h a n g i b i r r e e l s a yı o l s u n .
y
n
E ğ e r ∥P∥→0 i ç i n
∑ f ( x'k ) Δ x k = L
olacak
k=1
x
ş ek i l d e b i r L ∈ R s a yı s ı v a r s a P
p a r ç a l a n ı ş ı v e x 'k s a yı l a r ı n ı n s e ç i m i n d e n
bağımsız olarak f [a,b] arasında
i n t e g r a l l e n e b i l i r v e L ∈ R ye [ a , b ] d e f n i n
b e l i r l i i n t e g r a l i d e n i r. ( b u a r a l ı k t a y= f ( x )
f o nk s i yo n u e ğ e r n e g a t i f o lm u yo r s a b u
l im i t d e ğ e r i e ğ r i i l e x e k s e n i a r a s ı n d a
kalan alanı verir)
4
0
4
8
4 n−4
. f
+f
+f
+...+f
n
n
n
n
n
(( ) ( ) ( )
4
.
n
∥P∥→0 ye r i n e n→∞ a yn ı ş e y o l a r a k
d ü ş ü n ü l e b i l i r. Δ x=dx , Δ x→0
lim
(∑ (
Δ xk →0 k =1
)
b
b ye b e l i r l i i n t e g r a l i d e r v e b u n u
∫ f (x )dx
a
o l a r ak ya z a r ı z . a v e b s a yı l a r ı n a
integralin alt ve üst limitleri denir
Kısaca
lim
(
n
∑ f ( x 'k) Δ xk
Δ xk →0 k =1
)
b
=L =∫ f ( x ) dx
a
+2))
(( 0n +2)+( 4n +2)+( 8n +2)+...+( 4n−4
n
(
(
f x 'k ) Δ xk =L ∈ℝ o l u yo r s a b u
l im i t d e ğ e r i n e y= f ( x ) f o n k s i yo n u n u n a ’ d a n
))
4
2n−2
4
4
16n−8
. 2n+
. n = . ( 2n+2n−2 )= . ( 4n−2) =
n
n
n
n
n
16n−8
lim
=16
n
n→∞
www.matbaz.com
n
Ö ze t l e
(
)
)
Üst toplam
y=x+2
y
x
4
. f
n
4
.
n
4n
+f
( ( 4n )+f ( 8n )+...+f ( 4n−4
n ) ( n ))
(( 4n +2)+(8n +2)+...+( 4nn +2))
Örnek...1 :
f : [ 0,4 ]→R , f (x )=x+2f o nk i yo n u i l e x = 0 d o ğ r u s u
x = 2 d o ğ r u s u v e x e k s e n i yl e s ı n ı r l ı b ö l g e n i n
a l a n ı n ı R i em a n n t o p l am ı yl a b u l u n u z
4
2n+4
4
4
16n+32
. 2n+
.n = . ( 2n+2n+8 )= . (4n+8 )=
n
n
n
n
n
(
lim
n→∞
)
( 16n+32
)=16
n
Ve bu sonuçla birlikte
A T ⩽RT⩽ÜT
Ç ö züm
[ 0 , 4 ] a r a l ı ğ ı n ı n e ş i t b ö l ü nm e s i yl e h e r b i r
4−0 4
a r a l ık
= o l a r a k e l d e e d i l i r.
n
n
12. Sınıf Matematik Konu Anlatımı 2014−2015
4
olduğu için 16⩽RT =∫ ( x+2) dx⩽16
4
∫ ( x+2) dx=16
0
e l d e e d i l i r ( İ n t e g r a l h e s a b ın
0
t em e l t e o r em i i l e b e l i r l i i n t e g r a l l e r i R i em a n n
t o p l am l a r ın ı n l i m i t i ye r i n e b a şk a v e d a h a k ıs a
b i r yö n t em l e h e a p l a ya c a ğ ı z)
2/13
İNTEGRAL 6
BELİRLİ İNTEGRAL
BELİRLİ İNTEGRAL KURALLARI
b
1.
İNTEGRAL HESABIN TEMEL TEOREMLERİ:
İNTEGRAL HESABIN TEMEL TEOREMİ I
a
∫ f (x )dx =−∫ f ( x ) dx
a
b
f : [ a , b ] →R s ü r ek l i b i r f on k s i yo n v e
b
d ( ( )) ( )
F x =f x i s e ∫ f ( x )dx =F ( b )−F ( a ) o l u r.
dx
a
a
2.
∫ f (x )dx =0
a
b
b
3.
∫ k. f ( x ) dx=k. ∫ f (x ) dx
a
b
b
a
b
5.
a
c
b
∫ f (x )dx =∫ f (x ) dx +∫ f (x ) dx ,
a
a
h e s a p l a m ak i ç i n
R i e m a n n t o p l am ı i l e s o n u c a g i t m e k
ye r i n e f ( x ) f o nk s i yo n u n u n i l k e l i o l a n
F ( x ) g i b i b i r f o nk s i yo n d a i n t e g r a l i n
s ın ı r l a r ı n ı ya za r o l u ş a n f ar k ı ( F ' d e ü s t
s ın ı r d e ğ e r i n d e n a l t s ın ı r d e ğ e r i n i
ç ık a r a r a k ) c e v a p o l a r ak h e s a p l a r ız v e r i r.
∫ ( f ( x )±g ( x )) dx=∫ f ( x ) dx±∫ g( x ) dx
a
∫ f (x )dx if a d e s i n i
a
a
b
4.
Ya n i
b
Örnek...4 :
c<b
2
c
∫ xdx =?
1
6 . ( b - a ) . m i n (f ( x ) ) < ∫ f ( x ) dx =0< ( b a).max(f(x))
a
Örnek...2 :
15
15
∫ f ( x ) dx=10,
−1
15
(∫
−1
ve
∫ g (x )dx =8
−1
15
) (∫
f (x ) +g ( x ) dx .
−1
f ( x )−g( x ) dx
ise
)
www.matbaz.com
b
Örnek...5 :
3
∫ ( x3 +5x 2−7x +4) dx=?
−1
π
2
∫ sinx dx=?
Örnek...3 :
3
Örnek...6 :
7
2
0
∫ f (x )dx =−3 v e ∫ f (x )dx =5i s e ∫ f (x )dx =?
2
3
7
π
2
Örnek...7 :
∫ sinx.cosx dx=?
0
12. Sınıf Matematik Konu Anlatımı 2014−2015
3/13
İNTEGRAL 6
BELİRLİ İNTEGRAL
Örnek...8 :
2
∫(
0
Örnek...12 :
e
( lnx ) 2
∫ x dx =?
1
x
3x2 + dx=?
3
)
Örnek...9 :
π
∫π sin2 x. cosx dx =?
ln2
∫ (e
2x
Örnek...13 :
x
+e ) dx=?
2
Örnek...10 :
√3
dx
=?
∫ 1+x
2
1
UYARI
D e ğ i şk e n d e ğ i ş t i r m e ya p ı l d ı ğ ı n d a ye n i
d e ğ i şk e n e g ö r e s ı n ı r l a r t ek r a r
h e s a p l a n ı r s a e s k i d e ğ i ş k e n e d ö n ü lm e d e n
integral hesaplanabilir
www.matbaz.com
ln1
Örnek...14 :
1
∫ ( x2 +5x+1)2 (2x +5) dx=?
0
π
2
Örnek...15 :
∫ x.cosx dx=?
0
Örnek...11 :
3
∫ ( x−2)2 dx=?
2
Örnek...16 :
100
∫ logx dx=?
10
12. Sınıf Matematik Konu Anlatımı 2014−2015
4/13
İNTEGRAL 6
BELİRLİ İNTEGRAL
Örnek...17 :
Örnek...22 :
2
∫ x 5+x 3 dx =?
G r af i ğ i v e r i l e n y= f ( x )
f o nk s i yo n u n u n g r a f i ğ i n e
−2
y
7
y=f(x)
5
göre
∫ ( f ( x )+x.f ' ( x )) dx=?
4
3
3
5
x
Örnek...18 :
1
√3
Örnek...23 :
=?
∫ 1dx
+x2
3
1
Örnek...19 :
∫ √ sin x.cosx dx=?
0
www.matbaz.com
2
π
4
3
∫ f (x )dx =5 ise ∫ (7−f ( x )) dx=?
2
Örnek...24 :
2
8
∫ f (4x ) dx=60ise ∫ (1−f ( x )) dx=?
0
0
Örnek...20 :
3
x 15
∫ 1+x 4 dx=?
−3
e2
Örnek...21 :
Örnek...25 :
( )
dx=3 ise
∫ f lnx
x
e
5
2
∫ x. f ( x2 +1 )dx =?
1
1
∫ x.ln (x 2 +1) dx =?
0
12. Sınıf Matematik Konu Anlatımı 2014−2015
5/13
İNTEGRAL 6
BELİRLİ İNTEGRAL
Örnek...26 :
Örnek...30 :
y= f ( x ) f o nk i yo n u r e e l s a yıl a r d a t ü r e v l i v e x= 2
n ok t a s ı n d ak i t e ğ e t i x ek s e n i yl e p o z i t if yö n d e
45 o l ik a ç ı ya p ı yo r s a v e x = 3 ek s t r e m u m
n ok t a l a r ı n d a n b i r i n n i n a p i s i s i i s e
3
x.f ' ' ( x )−f ' ( x )
dx = ?
∫
x2
2
4
∫ √ 16−x2 dx
i n t e g r a l i n d e x= 4 s i n t d ö n ü ş üm ü
0
ya p a r a k t ek r a r i n t e g r a l i ya z ı n ı z
Örnek...27 :
ln2
ex
∫ 2+e2x dx i n t e g r a l i n d e
u=ex dönüşümü
0
ya p a r a k t ek r a r i n t e g r a l i ya z ı n ı z
Örnek...31 :
Örnek...28 :
256 6
x− 3 x
∫ √ 4 √ dx
1
√x
integralinde x=u12 dönüşümü
ya p a r a k t ek r a r i n t e g r a l i ya z ı n ı z ( u>0)
www.matbaz.com
y
y= f ( x ) f o nk i yo n u n u n g r a f i ğ i
ş ek i l d ek i g i b i d i r
5
∫ f (x )+x.f ' (x ) dx =?
3
4
3
y=f(x)
2
3
x
5
Örnek...32 :
t
∫ ( x2−4x−5) dx
integralinin alacağı sonuç en az
0
Örnek...29 :
k a ç t ır ?
A ( 3 , 2 ) n o k t a s ı n d a ye r e l m ak s i m u m , B ( - 2 , 3 )
n o k t a s ı n d a ye r e l m i n i m u m a s a h i p y= f ( x )
3
f on k s i yo n u i ç i n
∫ x.f '' (x ) dx d e ğ e r i n i
bulunuz
−2
12. Sınıf Matematik Konu Anlatımı 2014−2015
6/13
İNTEGRAL 6
BELİRLİ İNTEGRAL
ÖZEL TANIMLI FONKSİYONLARIN İNTEGRALİ
Örnek...35 :
3
{
x⩾0 i s e
f ( x )= 2x+1
3x 2
x<0
İ n t e g r a n d ı n d a p a r ç a l ı f o nk s i yo n v e ya
m u t l ak d e ğ e r l i f on k s i yo n i ç e r e n
integraller integralin alındığı sınırlar
i ç e r i s i n d e k ri t i k n o k t a i ç e r i yo r s a g ö r e
p a r ç a l a n a r ak i n t e g r a l l e r i a l ı n ı r.
∫ f ( x ) dx
−1
f : [ a , b ] →Rf on k s i yo n u [ a , b ] a r a l ı ğ ı n d ak i
b u l u n a n s o n l u s a yı d a k i a 0 , a 1 , a 2 , . . . , a n
s a yı l a r ı i ç i n s ü r e k s i z i s e b u n o k t a l a r a
g ö r e i n t e g r a l p a r ç a l a n ı r.
a1
b
Ya n i
a2
an =b
∫ f (x )dx =∫ f (x ) dx +∫ f (x ) dx +...+ ∫
a
a
a1
f ( x ) dx
an −1
Örnek...36 :
{
x
ise
f ( x )= 2 x⩾0
x+1
x<0
B u p a r ç a l am a yı g e n e l d e p a r ç a l ı
f o nk s i yo n d a v e ya m u t l ak d e ğ e r i n k ri t i k
n ok t a s ı n d a i h t i ya ç d u ya r s a k ya p a r ı z
1
∫ f ( x+2) dx
−3
Örnek...33 :
−2
∫ f (x ) dx
−4
www.matbaz.com
{
2
x
x⩾0 i s e
f ( x )= (e)
x x<0
Örnek...37 :
{
lnx
f ( x )= x
ex
x⩾e i s e
x<e
e2
∫ f (x )dx
1
Örnek...34 :
{
5
x 2 x<2
f ( x ) = x 3 2<x<3 f on k s i yo n u i ç i n ∫ f ( x ) dx
0
x+1 x⩾3
Örnek...38 :
5
∫∣x+2∣dx
1
Örnek...39 :
3
∫ x3|x−2|dx
1
12. Sınıf Matematik Konu Anlatımı 2014−2015
7/13
İNTEGRAL 6
BELİRLİ İNTEGRAL
Örnek...40 :
Örnek...45 :
3
∫ x3∣x−2∣dx
π
∫ (∣sinx∣+cos∣x∣) dx
1
π
−π
2
Örnek...41 :
π
2
Örnek...46 :
∫ sinx−√22
∫∣cosx∣dx
0
0
∣
∣dx
π
Örnek...42 :
∫∣cosx−sinx∣dx
0
2π
∫π
www.matbaz.com
Örnek...47 :
y
y=f(x)
R e e l s a yıl a r d a s ü r e k l i
o l a n f f on k s i yo n u n u n
t ü r e v i n i n g r a f i ğ i v e r i l i yo r.
f(3)-f(2)=?
2
x
-1
Örnek...43 :
√
1+cosx
dx
2
İNTEGRAL HESABIN TEMEL TEOREMİ II
f : [ a , b ] →R s ü r ek l i b i r f on k s i yo n v e
x
x
d ( F (x ) ) d
=
f ( t ) dt =f ( x )
F ( x )=∫ f (t ) dti s e
∫
dx
dx a
a
ya n i s ü r e k l i h e r f o nk s i yo n b a ş k a b i r
f on k s i yo n u n t ü r e v i d i r. B a ş k a b i r d e yi ş l e
t ü r e v v e i n t e g r a l i ş l em l e r i b i r b i r l e r i n i n
t e r s i i ş l e m l e r d i r.
(
Örnek...44 :
1
x2−4
∫ ∣x−2∣dx
0
12. Sınıf Matematik Konu Anlatımı 2014−2015
)
Örnek...48 :
d
dx
(
x
∫ sint dt
a
)
=?
8/13
İNTEGRAL 6
BELİRLİ İNTEGRAL
Örnek...49 :
d
dx
x
(∫
−2
Örnek...54 :
)
1
dt =?
t 2+1
d
dx
x3
(∫ )
t
d( e ) =?
ln2
Örnek...50 :
d
dx
(
x
)
∫ tant dt =?
√7
d
dx
Örnek...55
:
π
(∫ sintt )=?
e
GENELLEME (LEİBNİZ KURALI)
u( x )
F ( x ) = ∫ f (t ) dt o l a r a k v e r i l s i n
d (F (x ) ) d
=
dx
dx
u (x )
(∫ )
f ( t ) dt =f ( u ( x ) ) .u ' (x )−f ( v ( x )) . v ' ( x )
v(x )
Örnek...51 :
d
dx
cosx
(∫
)
t 2 +t dt =?
sinx
Örnek...52 :
d
dx
x2
(∫
)
tant dt =?
x
www.matbaz.com
v (x)
Örnek...56 :
x 2 +1
t
F ( x ) = ∫ e dt f on k s i yo n u n x= 1 n o k t a s ın d a k i
x+ 1
teğet denklemini bulunuz
Örnek...57 :
x2
2
F ( x ) = ∫ t dtf o nk s i yo n u n x d ö n ü m n ok t a s ın ın
x+ 2
apsisini bulunuz
Örnek...53
:
π
(( ))
2
∫π costdt
lim
x→2
x
ln ( x−1 )
12. Sınıf Matematik Konu Anlatımı 2014−2015
Örnek...58 :
x
F ( x ) =∫ t.et dt i s e F ' ( 1 ) k aç t ır ?
0
9/13
İNTEGRAL 6
BELİRLİ İNTEGRAL
1
DEĞERLENDİRME
5)
1
∫ 1+x2 dx=?
√3
3
1)
3
∫ f (x )dx =10 ve ∫ g ( x ) dx=8 ise
2
2
3
(∫
3
) (∫
( 4.f ( x )+3g (x ) ) dx .
2
(5. f ( x )−4g ( x ) ) dx
2
)
π
4
6)
∫ sin2xcosx dx=?
0
2
2)
2
∫ f (x )dx =6 ve ∫ ( 5−3.f ( x ) )dx =?
1
1
2
2
3)
2
( )=?
xn
∫ ∑ n!
1
n=0
www.matbaz.com
7)
∫ ( 3x2+3x ) dx=?
1
ln4
8)
∫ e−x dx=?
ln2
√3
1
4)
4
∫ x2−4 dx =?
0
12. Sınıf Matematik Konu Anlatımı 2014−2015
2
9)
∫
1
2
dx
dx=?
√ 1−x 2
10/
10/13
İNTEGRAL 6
BELİRLİ İNTEGRAL
−4
10)
2
1
∫ ( x+5)4 dx =?
15)
−3
∫ ( x15 +x7.cosx +sin9 x ) dx=?
−2
π
2
16)
2
1
11) ∫
dx=?
2
x.ln
x
1
17)
x+3
∫ √ x . √ x+6 dx=?
3
13)
2
x
∫ f ( 3 )dx=36 ise ∫ ( x+3−4.f (2x ) )dx =?
0
4
π
4
x ) dx=?
0
www.matbaz.com
12)
2
6
12
19
(
1−sin
∫π cosx .√ sinx
18)
∫ x.sinx dx =?
dx
2
∫ f (√ x ) √ x =3 ise ∫ 5x.f
1
√2
2
( x2 )dx=?
0
e
14)
∫ lnx dx =?
1
3
19)
∫ ( √ 9−x 2 ) dx integralinde x=3sina dönüşümü
0
yaparak tekrar integrali yazınız
12. Sınıf Matematik Konu Anlatımı 2014−2015
11/
11/13
İNTEGRAL 6
BELİRLİ İNTEGRAL
ln2
20)
ex
∫ 2+e2x dx
y
integralinde u=ex dönüşümü
24) y=f(x) fonkiyonu n grafiği
0
yaparak tekrar integrali yazınız
2
135O
şekildeki gibidir
x
5
∫ f (x )+x.f ' (x ) dx integralinin
y=f(x)
3
değerini bulunuz
21)
64
x−x
∫ √3
1
(
√x
)
dx integralinde x=u6 dönüşümü
yaparak tekrar integrali yazınız
a
25)
∫ ( 2x2−6x ) dx integralinin alacağı sayısal sonuç
0
π
2
22)
cot ( x+π ) dx=?
integralinde x=t+ π
∫ 1 +tan
(x−π )
2
0
dönüşümü yaparak tekrar integrali yazınız
www.matbaz.com
en az kaçtır?
{
1+x
4
x<1
1⩽x⩽3 fonksiyonu için ∫ f ( x ) dx
0
x−1 x>3
26) f ( x )= x
{3x
27) f ( x ) = 1+2x
23) y=f(x) fonkiyonu reel sayılarda türevli ve x=1
noktasındaki teğeti x eksenine paralel ve x=5
deki teğeti y-3x+2=0 doğrusuna dikse =?
5
∫
1
3
x⩾4 fonksiyonu için f ( x+3 ) dx
∫
x<4
−1
1
f '' ( x )
f ' (x )
dx+∫ 2 dx
x
x
5
4
28)
∫∣x−2∣dx
1
12. Sınıf Matematik Konu Anlatımı 2014−2015
12/
12/13
İNTEGRAL 6
BELİRLİ İNTEGRAL
3
29)
35) d
∫ x.∣x−2∣dx
dx
−1
x2
∫ d (lnt )
1
3π
2
30)
∫π ∣sinx∣dx
2
36) A( 1,2 ) noktasında teğeti y eksenine dik
,B(4,7) noktasında yerel ekstremuma sahip
4
y=f(x) fonksiyonu için
∫ x.f ' ' ( x ) dx değerini
1
bulunuz
4π
2
31)
∫π √ 1−cos2 xdx
32) d
dx
x 2+ 1
∫
tant dt
a
www.matbaz.com
3
37) [-2,4] aralığı Δ x= 6 olacak şekilde n tane
n
aralığa bölünüyor. x k ' k . aralığın orta noktası
olmak üzere lim
n→∞
n
(∑ ( (
k=1
)
3 x k ' )2−2xk ' ) . Δ x limitini
integralle ifade ediniz.
x
33) f ( x )= ∫ ( t 2 +1 ) dt veriliyor. f fonksiyonunun
√3 −2
dönüm noktasının apsisi nedir?
π
x
( )
∫π sint dt
34) lim
x→2
2
e x−2−1
12. Sınıf Matematik Konu Anlatımı 2014−2015
13/
13/13