İNTEGRAL DERS NOTU 1
fehmiekici.wordpress.com
İNTEGRAL
BİR FONKSİYONUN DİFERANSİYELİ
Tanım: f: [a,b] R, x f(x) fonksiyonu (a,b) aralığında türevli olmak üzere, x
değişkeninin değişme miktarı x ise f '(x). x ifadesine f(x) fonksiyonunun diferansiyeli denir
ve d(f(x)) ile gösterilir.
y = f(x)
dy
= f '(x) dy = f '(x). dx tir.
dx
Y = f(x) denklemi ile verilen fonksiyonun diferansiyeli
dy = f '(x). dx tir.
Örnek
f(x) = 2x ise, d(f(x)) nedir?
Çözüm
d(f ( x ))
dy
2
2
dx
dx
= 2 . dx tir.
Örnek
y = x3 +
1 2
x – 3x + 5 ise, dy nedir?
2
Çözüm
dy
= 3x2 + x – 3 dy = (3x2 + x – 3) dx tir.
dx
İNTEGRAL DERS NOTU 2
fehmiekici.wordpress.com
BELİRSİZ İNTEGRAL
Tanım: f(x) fonksiyonu [a,b] aralığında sürekli ve (a,b) aralığında türevli olsun.
Fı(x) = f(x) ise d(F(x)) = f '(x). dx tir.
c R için (F(x) + c)ı = Fı(x) = f(x) ise,
d(F(x) + c) = f(x) . dx olur.
Buna göre, F(x) + c ifadesine, f(x) fonksiyonunun “İlkeli” veya “Belirsiz İntegral”
denir.
UYARI: İntegral “türevi ya da diferansiyeli” belli olan fonksiyon nedir, sorusuna
cevap olarak çıkmıştır. Türevi bilinen bir fonksiyonun, türevi alınmadan önceki halini (İlkeli)
bulma işlemine, İntegral diyebiliriz.
BELİRSİZ İNTEGRALİN KURALLARI
a) a o ise a.f(x) dx = a. f(x) dx tir.
b) [f(x) g(x) h(x)] dx
= f(x) dx g(x) dx h(x) dx tir.
TEMEL İNTEGRAL KURALLARI
Kural 1
n -1 ise,
n
x dx
x n1
c (c R, c sabit)
n 1
Örnek
F(x) = (3x2 + 2x – 3) dx integralini hesaplayınız.
Örnek
F(x) = x dx (x > 0) integralini hesaplayınız.
İNTEGRAL DERS NOTU 3
fehmiekici.wordpress.com
Kural 2
a) f '(x) dx = f(x) + c
b)
f ( x) . f
n
ı
n 1
f ( x)
( x)dx
c
n 1
Örnek
(x2 + 4)2 . (2x) dx integralini hesaplayınız.
Örnek
x 2 2x 3.(2x 2)dx integralini hesaplayınız.
Kural 3
a)
b)
dx
ln x c
x
f ı ( x)
dx ln f ( x) c
f ( x)
Örnek
x3 x 1
x dx integralini hesaplayınız.
İNTEGRAL DERS NOTU 4
fehmiekici.wordpress.com
Örnek
2dx
3
2x 3 x 2 integralini hesaplayınız.
Kural 4
a)
e dx e
b)
e
c)
x
a dx
d)
f (x) ı
a .f (x)dx
x
f ( x)
x
c
. f ı ( x)dx e f ( x ) c
ax
c
ln a
a f (x)
c
ln a
Örnek
e3x+1 dx integralini hesaplayınız.
Örnek
1
x
4x
2x
e e e 2 dx ifadesinin integralini hesaplayınız.
İNTEGRAL DERS NOTU 5
fehmiekici.wordpress.com
Kural 5
A) 1) sin xdx cos x c
1
2) sin(ax b)dx cos(ax b) c
a
B) 1) cos xdx sin x c
1
2) cos(ax b) sin(ax b) c
a
C) 1)
dx
1 tan x dx cos x
2
2
= sec 2 xdx tan x c
2)
D) 1)
1 tan
2
ax dx
1
tan ax c
a
dx
1 cot x dx sin x
2
2
= (cos ec 2 x )dx cot x c
2)
1 cot
2
1
ax dx cot ax c
a
Örnek
(cos3x – sin2x) dx integralini hesaplayınız.
Örnek
tan x dx integralini hesaplayınız.
İNTEGRAL DERS NOTU 6
fehmiekici.wordpress.com
Örnek
f (x)
sin x
dx integralini hesaplayınız.
cos 2 x
Örnek
(tan5x + tan3x) dx integralini hesaplayınız.
TERS TRİGONOMETRİK FONKSİYONLARIN İNTEGRALİ
a)
b)
c)
1
1 x2
1
1 x2
dx Arc cos x c
du
a u
2
2
du
a2 u2
1
1 x
a
2
a
2
dx Arc sin
u
c
a
dx Arc cos
u
c
a
2
dx Arc tan x c
2
dx Arc cot x c
1
1 x
d)
dx Arc sin x c
du
1
u
Arc tan c
2
a
a
u
du
1
u
Arc cot c
2
a
a
u
İNTEGRAL DERS NOTU 7
fehmiekici.wordpress.com
Örnek
dx
4 x2
integralini hesaplayınız.
Örnek
cos x
1 sin
2
x
dx integralini hesaplayınız.
DEĞİŞKEN DEĞİŞTİRME (DÖNÜŞÜM) YÖNTEMİ
a) f(x) . dx integralinde x = g(t) diyelim. x = g(t) ise, dx = gı(t) dt dir.
f(x) dx = f(g(t)) . gı(t) dt yazılırsa, integral t türünden ifade edilmiş olur.
Örnek
F(x) =
2.( x 3 2).3x 2
(x 3 2) 2 3 dx olarak tanımlıdır.
F(-1) = ln2 ise, F(0) kaçtır?
İNTEGRAL DERS NOTU 8
fehmiekici.wordpress.com
İNTEGRAL DERS NOTU 9
fehmiekici.wordpress.com
İNTEGRAL DERS NOTU 10
fehmiekici.wordpress.com
İNTEGRAL DERS NOTU 11
fehmiekici.wordpress.com
İNTEGRAL DERS NOTU 12
fehmiekici.wordpress.com
İNTEGRAL DERS NOTU 13
fehmiekici.wordpress.com
İNTEGRAL DERS NOTU 14
fehmiekici.wordpress.com
İNTEGRAL DERS NOTU 15
fehmiekici.wordpress.com
İNTEGRAL DERS NOTU 16
fehmiekici.wordpress.com
İNTEGRAL DERS NOTU 17
fehmiekici.wordpress.com
İNTEGRAL DERS NOTU 18
fehmiekici.wordpress.com
İNTEGRAL DERS NOTU 19
fehmiekici.wordpress.com
İNTEGRAL DERS NOTU 20
fehmiekici.wordpress.com
İNTEGRAL DERS NOTU 21
fehmiekici.wordpress.com
İNTEGRAL DERS NOTU 22
fehmiekici.wordpress.com
İNTEGRAL DERS NOTU 23
fehmiekici.wordpress.com
İNTEGRAL DERS NOTU 24
fehmiekici.wordpress.com
Örnek
x
2
dx
integralini hesaplayınız.
3x 2
Örnek
2x 2 2x 1
x 3 x 2 dx integralini hesaplayınız.
İNTEGRAL DERS NOTU 25
fehmiekici.wordpress.com
KISMİ İNTEGRAL
İNTEGRAL DERS NOTU 26
fehmiekici.wordpress.com
İNTEGRAL DERS NOTU 27
fehmiekici.wordpress.com
İNTEGRAL DERS NOTU 28
fehmiekici.wordpress.com
BELİRLİ İNTEGRAL
BELİRLİ İNTEGRALİN ÖZELLİKLERİ
İNTEGRAL DERS NOTU 29
fehmiekici.wordpress.com
Örnek
3
2xdx integralini hesaplayınız.
1
Örnek
3
(3x 2)dx 14 ve a + b = 6 olduğuna göre, b kaçtır?
1
İNTEGRAL DERS NOTU 30
fehmiekici.wordpress.com
İNTEGRAL DERS NOTU 31
fehmiekici.wordpress.com
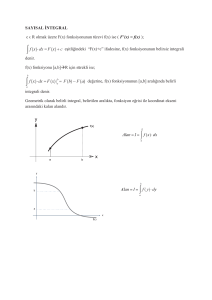
Teorem: f: [a,b] R sürekli bir fonksiyon ise,
F(x) =
x
a
f ( t )dt ile tanımlı;
F: [a,b] R ye fonksiyonu (a,b) aralığında türevlenebilir ve x (a,b) için,
F(x) =
x
a
1) F(x) =
f ( t )dt Fı(x) = f(x) tir.
h(x)
a
f ( t )dt ise
Fı(x) = hı(x) . f(h(x)) tir.
2) F(x) =
h(x)
g(x)
f ( t )dt ise
Fı(x) = hı(x) . f(h(x)) – gı(x) . f(g(x)) tir.
Örnek
f(x) =
x
2
e t 1dt ise, fı(1) kaçtır?
2
İNTEGRAL DERS NOTU 32
fehmiekici.wordpress.com
ÖZEL TANIMLI FONKSİYONLARIN İNTEGRALLERİ
MUTLAK DEĞER FONKSİYONU
f: [a,b] R ye sürekli f fonksiyonu tanımlasın.
b
a
f ( x ) dx integrali hesaplanırken;
önce fonksiyonun [a,b] de işareti incelenir. Fonksiyonun işaretine göre aralıklarda integralin
değeri bulunur.
Örnek
5
2
x 4 dx integralinin değeri nedir?
Örnek
/6
Örnek
cos x dx integralinin değeri nedir?
İNTEGRAL DERS NOTU 33
fehmiekici.wordpress.com
Örnek
Örnek
İNTEGRAL DERS NOTU 34
fehmiekici.wordpress.com
EĞRİLERLE SINIRLI DÜZLEMSEL BÖLGELERİN ALANLARININ BULUNMASI
1.
İNTEGRAL DERS NOTU 35
fehmiekici.wordpress.com
3.
4.
İNTEGRAL DERS NOTU 36
fehmiekici.wordpress.com
6.
7.
8.
İNTEGRAL DERS NOTU 37
fehmiekici.wordpress.com
Örnek
f(x) = x2 + 2 eğrisi x ve y eksenleri ile x = 2 doğrusu tarafından sınırlanan düzlemsi
bölgenin alanı kaç br2 dir?
Örnek
f(x) = x3 – 4x eğrisinin x ekseniyle sınırladığı düzlemsel bölgenin alanları toplamı kaç
br2 dir?
İNTEGRAL DERS NOTU 38
fehmiekici.wordpress.com
İKİ EĞRİ TARAFINDAN SINIRLANAN DÜZLEMSEL BÖLGELERİN ALANLARI
f(x) ve g(x) fonksiyonları [a,b] aralığında sürekli ve f(x) > g(x) olsun.
Bu eğriler tarafından sınırlanan düzlemsel bölgenin alanı;
S=
b
[f (x) g(x)]dx
a
tir.
İNTEGRAL DERS NOTU 39
fehmiekici.wordpress.com
İNTEGRAL DERS NOTU 40
fehmiekici.wordpress.com
İNTEGRAL DERS NOTU 41
fehmiekici.wordpress.com
8.
9. f(x) = -x2 – x + 2 ve g(x) = 2x + 2 eğrileri arasında kalan taralı alanı bulunuz.
10. f(x) = -x2 + 4x ve g(x) = x2 + 2x eğrilerinin sınırlandığı alanı bulunuz?
İNTEGRAL DERS NOTU 42
fehmiekici.wordpress.com
İNTEGRAL DERS NOTU 43
fehmiekici.wordpress.com
İNTEGRAL DERS NOTU 44
fehmiekici.wordpress.com
6. y = x2 + 1 parabolünün oy ekseni etrafında 3600 dönmesinden [2,4] aralığında oluşan
cismin hacmini bulunuz.
İNTEGRAL DERS NOTU 45
fehmiekici.wordpress.com
İNTEGRAL DERS NOTU 46
fehmiekici.wordpress.com
İNTEGRAL DERS NOTU 47
fehmiekici.wordpress.com
İNTEGRAL DERS NOTU 48
fehmiekici.wordpress.com
İNTEGRAL DERS NOTU 49
fehmiekici.wordpress.com
İNTEGRAL DERS NOTU 50
fehmiekici.wordpress.com
İNTEGRAL DERS NOTU 51
fehmiekici.wordpress.com
İNTEGRAL DERS NOTU 52
fehmiekici.wordpress.com
İNTEGRAL DERS NOTU 53
fehmiekici.wordpress.com
İNTEGRAL DERS NOTU 54
fehmiekici.wordpress.com
İNTEGRAL DERS NOTU 55
fehmiekici.wordpress.com
İNTEGRAL DERS NOTU 56
fehmiekici.wordpress.com