opampların ıntegral alan devre olarak kullanılması

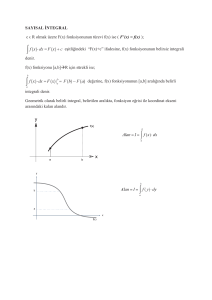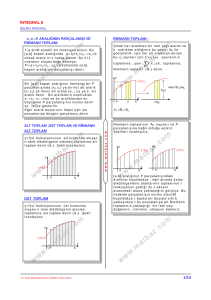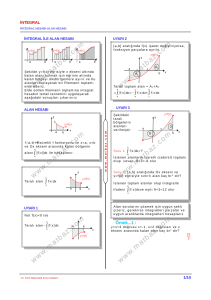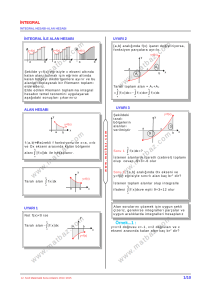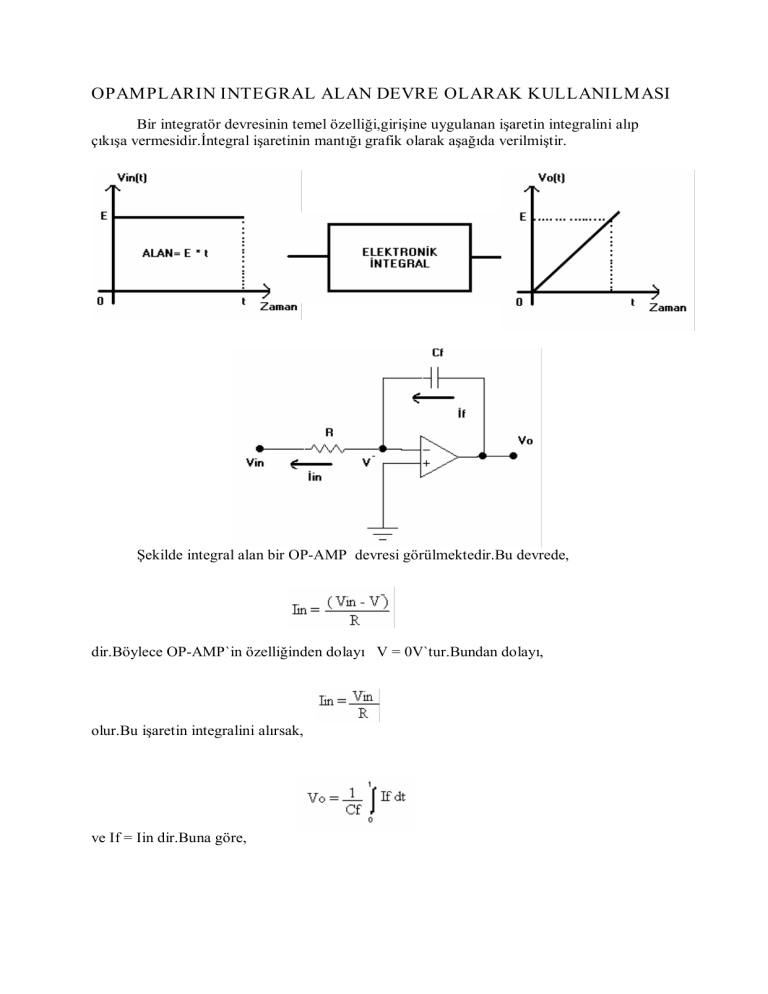
OPAMPLARIN INTEGRAL ALAN DEVRE OLARAK KULLANILMASI Bir integratör devresinin temel özelliği,girişine uygulanan işaretin integralini alıp çıkışa vermesidir.İntegral işaretinin mantığı grafik olarak aşağıda verilmiştir. Şekilde integral alan bir OP­AMP devresi görülmektedir.Bu devrede,
dir.Böylece OP­AMP`in özelliğinden dolayı V = 0V`tur.Bundan dolayı, olur.Bu işaretin integralini alırsak, ve If = Iin dir.Buna göre,
olarak bulunur.Matematiksel integral bir eğri altında kalan alanı temsil eder.Bu OP­AMP devresinde giriş ofset geriliminin OP­AMP`ı doyuma götürmesini götürmek için C kapasi­ törüne paralel bir R geri besleme direnci bağlamak gerekir.Burada OP­AMP`ın (+) giriş ucu na bir ikinci direncide toplayıcı devredeki anlamıyla bağlayıp şaselendirmemiz gerekmekte­ dir.Bu anlam şudur. Bir OP­AMP`da girişlerin ikiside 0V olduğunda çıkışta bir gerilim gözükür.Bu gerilime çıkış Ofset gerilimi denir.Ofset geriliminden dolayı burada bir akım oluşur.Bu akım OP­AMP ın transistörlü uygulamalarında ve frekans cevabında zararlı etkilere sahiptir.Bunu önlemek için Rc direnci OP­AMP`ın + girişine bağlanır. Aşağıda pratikte kullanılan bir elektronik integratör devresi görülmektedir. Vin bir sinüs dalgası olduğunda, olur.
Bu devreye uygulanan işaret AC olduğundan dolayı bir frekans vardır.Burada Vc = Rf
eşitliğinden Rf bileşeni kritik frekansı gösterir.Eğer Xc yi açarsak, w = 2 � Fc olur.Buradanda, bulunur.Burada Fc kritik frekanstır.Sonuç olarak kritik frekans, olur.Bu devrenin kazancı ise, dir.Bu yaptıklarımızı örneklerle açıklayalım. Örnek­1: Şekildeki integratöre bir sinüs dalgası uygulandığında , a)Kritik frekansı (Fc)`yi bulunuz? b)Giriş gerilimi olarak 60mV dc uygulandığında Vo çıkış gerilimini bulunuz. c)Rc=?
ÇÖZÜM: a)Verilen değerler formülde yerine konursa, bulunur. b)Bir integratöre DC bir gerilim uygulandığında kapasitör by pass edileceğinden dolayı devre bir eviren yükselteç gibi davranır.Sonuç olarak, bulunur. c) bulunur. OPAMPLARIN TÜREV ALAN DEVRE OLARAK KULLANILMASI Şekilde ideal bir elektronik türev alıcı devre görülmektedir.
Dikkat edilecek olursa integral devresindeki direnç ile kondansatörün yerleri değiştirilerek türev devresi yapılmıştır. Vi = 0V olduğunan Kirşof kanunlarını kullanırsak bulunur.Buradan da Vo değeri çekildiğinde , olduğu görülür. Yukarıda ideal bir türev devresinden bahsettik ama pratik türev devresine birde giriş di­ renci eklenir ve böylece devrenin daha kararlı ve az hatayla çalışması sağlanır. NOT:Sinüs bir işaretin türevi kosinüs işaret şeklinde olacaktır.Kosinüs bir işatetin türevi ise eksi sinüs bir işaret şeklinde olacaktır.Türev devreleri üçgen dalga şekillerini kare dal­ ga şekline çevirirler.
İntegral devresinde olduğu gibi türev devresinde de kritik frekans vardır.Bu frekans Xc = R1 eşitliğinden faydalınarak bulunur. Buradan da Fc değeri çekilirse, bulunmuş olunur. Örnek: 200Hz`e kadar olan sinyallerin türevini alan devreyi tasarlayınız. Çözüm: Burada integratör devresinin tersine Fc kritik frekansı verilen 200Hz in 10 katı büyüklükte olması gerekir.Zaten işlem bakımından integratör ile türev tam birbirinin Tersi işlem yapmaktadır.Buna göre; Fc = 10 * 200Hz = 2KHz Bulunur.Eşitlikte yerine konursa,
dir.Fakat burada C kondansatörününde seçilmesi gerekmektedir.C = 0,1�F alıp eşitlikte yerine koyalım ve eşitlikten R1`i çekelim. bulunur.