Slayt 1 - Asaf VAROL

Prof. Dr. Asaf Varol
2012-2013 Bahar Dönemi
1
2

Newton-Raphson yaklaşım metoduna benzer.

Analitik olarak türevin hesaplanmasına ihtiyaç duymadığı için farklıdır,
bu büyük bir avantaj sağlar.
F(xi) = [F(xi) - F(xi-1)]/(xi – xi-1)

Dezavantajı, bu ilk iki tahminin birinin yerine gerekmesidir.
3
4

Yüksekliği h, boru çapı D ve kuleye bağlı düşey aşağıya doğru
akan ve sonrasında yatay olarak arzu edilen dağıtım noktasına
ulaştırılan L uzunluğundaki boru içerisinden su geçmektedir. Bu
sistemde akış debisi olan Q için aşağıdaki denklem verilmektedir.
Secant yöntemini kullanarak köklerini bulunuz.
5
6
7

Bazı durumlarda, bir kök birden fazla kez kök rolünü yerine
getirebilmektedir. Örneğin denklemde
F(x) = x3 - x2 - x + 1= (x + 1)(x - 1)2 = 0
üç kök vardır, öyleki x = -1, ve x = 1 ile ikisinin katı

l’Hospital
kuralı
değişebilmektedir.
kullanılarak,
Newton-Raphson
metodu
xi+1 = xi - F(xi)/F(xi)
Veya, ikinci türevi de sıfır ise l'Hospital‘ kuralı aşağıdaki denklemi
elde etmek için bir kez daha uygulanabilir.
xi+1 = xi - F(xi)/F(xi)
8
9

Problem: Newton-Raphson metodunu polinom denklemine uygulayınız.
F(x) = x3 - 3x2 + 3x - 1 = (x - 1)3 = 0

Çözüm: İlk önce verilen fonksiyonda bir değişiklik olmadan Newton-Raphson
metodunu uygularız. Metotta gösterilen x0 = 0, 0.5, 0.9, ve 1.5 başlangıç
değerlerinin hiçbiri için bir noktada birleşmez. Bu olaydaki iterasyonlar da
0.2504306 ve 0.4258722 arasında salınım yapmaktadır. Fakat eğer aşağıdaki yer
değiştirmeyi yaparsak
U(x) = F(x) ve U(x) = F(x)
ve aynı metodu uygularsak
xi+1 = xi - U(xi)/U(xi)
Metot , 24 iterasyonda kök olan x=.9999999 'e 1.0E-07'ye bağlı bir hata ile yakınsar
ve x=0.0 değeri ile başlar.
10
Önceki metotların N değişken ile N denklemli sisteme
genişletilmesi
 Tartışmamız doğrusal olmayan denklemlerin aşağıdaki sistemler ile
çözümüyle sınırlı kalacaktır:

F(x,y) = 0
G(x,y) = 0

Örneğn,
x2 + y2 - 2 = 0
-exp(-x) + y2 - 1 = 0
11

Jacobi metodu, denklem sistemlerinin bir sabit nokta iterasyon metoduna
genişlemesidir.

Denklemlerin
x = f(x,y)
y = g(x,y)
F(x,y) = 0
G(x,y) = 0
dönüştürülmesi gerekmektedir .
Gerçek iterasyon bir denklem ile bir değişkenin durumuna benzer
xi+1 = f(xi,yi)
yi+1 = g(xi,yi)
12

Yakınsama kriteri- (xr, yr) kökünün komşuluğu
13

Problem: Jacobi İterasyon Metodunu kullanarak aşağıdaki denklem sistemlerini
çözünüz.
x - 5 + exp(-xy) = 0
y - 1 + exp(-0.5x)cos(xy) = 0

Çözüm: İlk olarak formdaki denklemleri yeniden yazınız x = f(x, y), y = g(x,y)
x = 5 - exp(-xy)
y = 1 - exp(-0.5x)cos(xy)


İlk tahmin olan x0 = 0, y0 = 0 ile başlarız ve 1.e-07'ye bağlı bir hata ile Jacobi
metodunu uygularız. Sonuçlar, Jacobi iterasyon yaklaşımının 20 iterasyonda kök
x=4.9926, y=0.98372 e yakınsadığını gösterenTablo 2.5.1 de gösterilmektedir. Not:
x ve y'deki mutlak hata, durdurma kriteri olarak kullanılır.
ERROR = (errorx2 + errory2)1/2 < errbound.
14
%Jacobi Iteration Method
x0=0.0;
y0=0.0
E=1.0E-4;
%
%---writing out headers to the file 'jacobimethod.dat'
%
fid=fopen('jacobi.dat','w');
fprintf(fid,'Roots of Equations x-5+exp(-xy)=0 \n\n')
fprintf(fid,'Roots of Equations y-1+exp(-0.5x)cos(xy)=0 \n\n')
fprintf(fid,'Using Jacobi Method \n')
fprintf(fid,'iter x
y ErrorX ErrorY \n');
fprintf(fid,'------------------------------------------\n');
%
%---entering the loop to determine the root
%
15
for i=1:100
x1=5-exp(-x0*y0);
y1=1-exp(-0.5*x0)*cos(x0*y0);
errorx=abs(x1-x0);
errory=abs(y1-y0);
%---writing out results to the file 'jacobi method.dat'
%
fprintf(fid,'%4.1f %7.4f %7.4f %7.4f %7.4f \n',i,x1,y1,errorx,errory);
%
if abs(x1-x0)<E&abs(y1-y0)<E
break;
end
x0=x1;
y0=y1;
end
fclose(fid)
disp('Roots approximation=')
x1,y1
16
17


Jacobi iterasyon metoduna benzer.
Hesaplamalar için güncelleştirilmiş x ve y değerlerini (yani
yaklaşık kökleri) kullanması açısından farklılaşır
18

İki doğrusal olmayan denklem içersin;

F(x,y) = 0
G(x,y) = 0
Taylor serisi genişlemesi bir fonksiyon olan F(x, y) için
burada ( )x ve ( )xx, x yoluyla birinci ve ikinci kısmi türevleri göstermektedir, ve
( )y , ( )yy ve ( )xy için de benzer şekildedir.
19

Sağdaki alandaki ilk üç terimi içermektedir

Alanları doldurduktan sonra x ve y için bu denklemler çözülür
Burada J Jacobian’dır ve şu şekilde tanımlanır
J = (FxGy - GxFy)
20

Sadece iki terimi tutarız ve böylece denklemleri basitleştiririz,
21

Köklerin yeni tahmininde 'güven' ifade edilir.
Underrelaxation 0 < < 1
Overrelaxation - 1 < < 2

Newton metodu şöyle uygulanabilir;


22


Çeşitli mühendislik uygulamalarında, Lazer Doppler Anamometresi (LDA)
kullanılarak sıvı hız ölçümleri yapılır. Bu, birbirini kesen yarıçapları verilen iki
çemberin merkezi konum koordinatlarını belirlemek için gereklidir. Bu durumda
genelliği kaybetmeden, biri çemberin merkezindeki koordinat sisteminin orjinine
koyulabilir, bunun sonucunda denklemler;
(xc,yc) ikinci çemberin merkezinin koordinatlarıdır. Örneğin xc =1, yc
=1, r1=1, r2=1, bu iki çemberin kesişim noktalarını bulabilirsiniz.
23

Çözüm: İki denklem için türetilmiş Newton-Raphson iterasyon metodu, yukarıda verilen
denklemin köklerini kolaylıkla bulmada kullanılabilir.

Kısmi türevler
Fx = 2x ; Fy = 2y ; Gx = 2(x-1) ; Gy = 2(y-1)

Ve Jacobian şu şekilde verilir:
J = (FxGy - GxFy)
( )x x'e göre kısmi türevi ifade eder ve y için de aynıdır. Yukarıdaki denklemlerin tam kökleri
denklemin (1,0) ve (0,1) kontrolü ile bulunabilir. İlk kök için bir başlangıç tahmini x=0.5 ,
y=0.1dir ve ikinci kök için x=0.1, y=0.5'dir. Kökler şu şekilde bulunmuştur:
(i) xr = 1.000013, yr =-1.310190e-05;
(ii) xr = -1.310190e-05, yr = 1.000013
24

Aşağıdaki şekilde görüldüğü gibi bir nesnenin sönümlü salınımı Newton'un ikinci
yasası tarafından yönetilir.
Şekil C.2.3a sönümlü kütle-yay sistemi

(kütle) (ivme) = (cisme etki eden net kuvvet)

Bu problem için denklem şu şekilde yazılabilir;
m a = - cv - kx
m kütle (kg olarak), a bir hızlanma, c yay sabiti sönüm katsayısı (kg/s), k (kg/s)
yaylanma katsayısı ve x bir denge konumundan yer değiştirme mesafesidir.
Yukarıdaki denklem şu şekilde de yazılabilir:


x = x0 ; v = 0. at t =0.
25

Bu sorunun analitik çözümü bunun bir salınım hareketi olduğu gerçeğini bilerek
bulunabilir ve bu viskoz bir sıvı ile sönümlüdür, böylece yer değiştirme uzun bir süre için
sıfıra gitmelidir, örneğin t nin sonsuza gitmesi gibi. Formun bir çözümü
x =x0 exp(-bt) [ ACos(t) + BSin(t) ]
Başlangıç koşulları ile yetinmek yerine şunu elde etmeliyiz



1)
2)
3)
A = 1 ; B = b/
Önerilen çözüm, Cos(t) ve Sin(t) ‘in sıfıra doğru katsayılarının eşitlenmesi
diferansiyel denklem için önerilen yedekleme çözümüdür (diferansiyel eşitleme bir süre
için sıfır olmalıdır) iki bilinmeyen için aşağıdaki ilişki verilir;
b = c/(2m) ;  = [ (k/m) - (c2/4m2)]1/2
Anlamlı bir çözüm için şu olmalıdır
c2 < 4mk
c= 100 kg/s, k = 10,000 kg/s2, ve m=50 kg verilmiştir.
Nesnenin salınımının %10'dan az olması durumunda bu ilk yer değiştirme olur ve
sonra zamanı belirleyin.
Nesnenin denge noktasını geçmesi durumunda ilki zamanı belirleyin. x=0.
c ve k'nın yukarıdaki değerlerini göz önüne alarak nesne ilk defa t=0.20 saniyede iken
sıfır pinti geçen m yi belirleyin
26


Çözüm (i): Önce b ve  parametrelerini hesaplarız :
b =1. sec-1 ;  =14.11 sec-1
Problem (i) yi çözmek için herhangi bir sayısal metot kullanmak gerekli değildir.
Ancak bunun genel davranışını elde etmek için zamanın bir fonksiyonu olarak bu
fonksiyonu çizeriz. Şekil C2.3b nesnelerin genlik bozulması ile periyodik bir şekilde
salınımını gösterir. Alan bilgileri şu şekildedir:
Sin(t) = 0. veya Cos(t) = 1

Fonkisyonun yerel bir maksimum ve minimumu vardır. Böylece;
0.1 = exp(-bt) [1.0 +0.0]
ilk kısım için cevap, t = 2.3 saniye olarak bulunur.
27

Çözüm (ii): Bölüm (ii) şu çözümü gerektirir;
0 = exp(-bt) [ Cos(t) + c/(2m)Sin(t) ]

exp(-bt) hiçbir zaman sıfır olmadığında, şu denklem ile iki bölüme ayırırız;
F(t) =Cos(t) + c/(2m)Sin(t) ] = 0.

Parametrelerin verilen değerleri ile ve alt ve üst değerleri olan tlower = 0., tupper=0.2
ile Bisection metodu kullanılır, Bölüm (ii)’nin cevabını aşağıdaki şekilde buluruz;
t = 0.11636 seconds

Bu problem ayrıca Newton-Raphson metodu ile de çözülebilir.
28
29

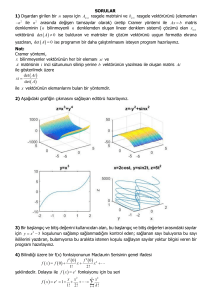
Bölüm (iii) Çözümü: Bu durumda bağımlı değişken zaman değil, kütle olan m'dir. Bu nedenle
şekillerde görüldüğü gibi bağımsız değişken m fonksiyonunu çizeriz. İlk şekil 0.5 kg aralığındaki
fonksiyonu tarama ile oluşturulur. Daha önce belirtildiği gibi bazı analitik analizleri kullanmadan ve bazı
mühendislik yargılarını kullanmadan bu denklemin yaklaşık köklerinin ne olacağını tahmin etmek zordur.
Bu problem sabit bir süre için iyi bir örnektir, bu durumda, sadece bir kütle, m olduğunda t=0.2 s olduğu
görülmektedir. Grafiklerden bunun durum olmadığı görülmektedir. Grafik dikatlice incelendiğinde şu
aralıkta kökleriin olduğu görülmektedir:
(0.5, 1.0) ; (1.5, 2.0) ; (2.5, 3.0) ; (5.5, 6.0) ; (16.5, 17.0) ; (153.5, 154)


Bununla birlikte ilk şekilden bütün bu noktaları bulmak zordur. Bunun için, grafiğin bu kısmı ikinci şekilde
genişletilir ve yeniden çizilir . Bu fonksiyon için m<0.5 doğrultusunda tablodaki değerler irdelenir. Bu
yüzden , bölüm (iii)ün uygun bir açıklaması için çözüm aralığını belirtmek gerekir. Örneğin şu şekilde
olabilir;
“Nesne, denge noktası olan (x=0) dan t=0.2 saniyede geçer gibi (10,20) aralığında m'nin muhtemel
değerlerini belirleyin..” Bu problemi çözmek için aşağı ve yukarı 10 ve 20 sınırı ile Bisection metodunu
uygularız. Bu aralıktaki kökler;
1.E-04’e bağlı bir hata ile
m = 16.861 kg
30
31
32





Celik, Ismail, B., “Introductory Numerical Methods for Engineering
Applications”, Ararat Books & Publishing, LCC., Morgantown, 2001
Fausett, Laurene, V. “Numerical Methods, Algorithms and
Applications”, Prentice Hall, 2003 by Pearson Education, Inc., Upper
Saddle River, NJ 07458
Rao, Singiresu, S., “Applied Numerical Methods for Engineers and
Scientists, 2002 Prentice Hall, Upper Saddle River, NJ 07458
Mathews, John, H.; Fink, Kurtis, D., “Numerical Methods Using
MATLAB” Fourth Edition, 2004 Prentice Hall, Upper Saddle River, NJ
07458
Varol, A., “Sayisal Analiz (Numerical Analysis), in Turkish, Course
notes, Firat University, 2001
33