3. Ders
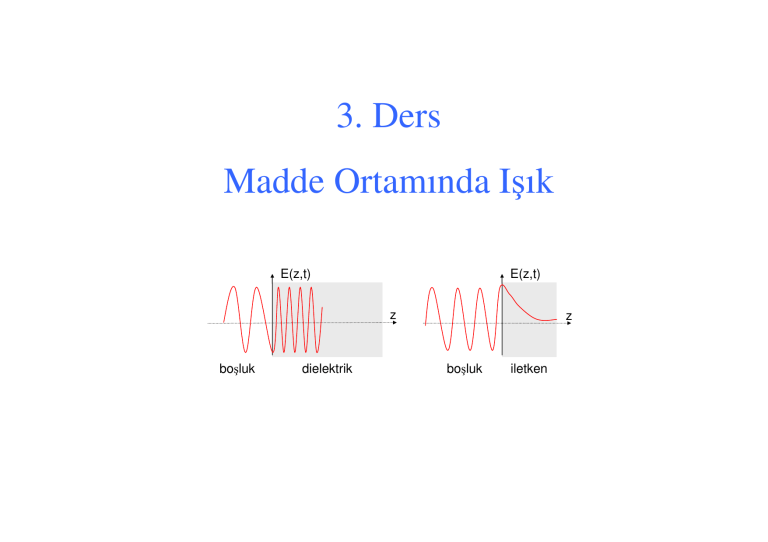
Madde Ortamında Işık
E(z,t)
E(z,t)
z
boşluk
dielektrik
z
boşluk
iletken
Bu bölümü bitirdiğinizde,
•
•
•
•
•
Işığın madde ortamında (dielektrik ve iletken) davranışı,
Kutuplanma vektörü,
Kırılma indisi,
Karmaşık kırılma indisi,
Soğurma katsayısı
konularında bilgi sahibi olacaksınız.
2
Üçüncü Ders: İçerik
•
•
•
•
•
•
•
Madde Ortamında Maxwell Denklemleri
Dielektrik Ortamda Maxwell Denklemleri
Dipol Momenti
Kutuplanma Vektörü
Kırılma İndisi Tanımı
Metal Ortamda Maxwell Denklemleri
Optik Sabitler
3
Madde Ortamında Işık-1
Maxwell denklemleri
(1)
(2)
(3)
(4)
r r ρ
∇ .E =
r r εo
∇ .H = 0
r
r r
∂H
∇ × E = − µo
∂t
r
r r
∂E r
∇ × H = εo
+J
∂t
Boşluk için yukarıdaki denklemleri çözüp, hem E hem de H alanının dalga denklemini
sağladığını göstermiştik.
Bu derste, Maxwell denklemlerini madde ortamı için yazıp çözmeye çalışacağız.
Birbirinden farklı iki tür ortamdan bahsedebiliriz. Bunlar;
• Dielektrik Ortam
• İletken Ortam
4
Madde Ortamında Işık-2
Dielektrik Ortam: J=0 ( Dielektrik ortam veya yalıtkan ortam veya saydam ortam) ρserbest=0
Metalik Ortam:
J≠0 ( İletken ortam veya metalik ortam veya yansıtıcı ortam) ρserbest=0
e
e
e
e
iyon
elektron
e
e
Dielektrik
ρ=0, J=0
Net yük yoğunluğu sıfırdır ve serbest
dolaşan yükler bulunmaz.
Metal
ρ=0, J≠0
Net yük yoğunluğu sıfırdır ancak serbest
dolaşan yükler (elektronlar) bulunur.
5
Madde Ortamında Işık-3
Madde ortamı söz konusu olunca neleri bilmek isteriz?
• Maddenin, dış elektrik alana tepkisi nasıldır?
• Bu elektrik alan elektromanyetik dalgayı oluşturan elektrik alan
(optik alan) bileşeni olduğunda maddenin tepkisi nasıl olur?
• Malzemenin elektrik alana tepkisini karakterize eden nicelikler
ile maddenin optik sabitleri arasındaki ilişki nasıldır?
• Ortamın tepkisinin ışığın frekansına bağlılığı nasıldır?
6
Madde Ortamında Işık-4
Durum I: J=0 ( Dielektrik ortam veya yalıtkan ortam veya saydam ortam) ρserbest=0
Dielektrik malzemeleri (SiO2 gibi) mükemmel yalıtkan olarak düşüneceğiz
(1)
(2)
(3)
(4)
Boşluk
r r
∇ .E = 0
r r
∇ .H = 0
r
r r
∂H
∇ × E = − µo
r∂t
r r
∂E
∇ × H = εo
∂t
Madde Ortamır r
r r ρ
−∇.P
∇.E = ind =
εo
r r εo
∇ .H = 0
r
r r
∇ .D = 0
r
r r
D ≡ εo (E + P)
r r
∂H
∇ × E = − µo
r∂t
r r
∂E
∇ × H = εo
∂t
• Madde ortamında Maxwell Denklemleri, boş uzayda yazıldığı forma indirgenerek bilinen
çözümler uygun şekilde düzenlenebilir.
• Dış alanlar (ışığın elektrik ve manyetik alanı) ortamdaki yük dağılımını değiştireceğinden bu
etkiyi göz önünde bulundurarak Maxwell denklemlerini düzenlememiz gerekecektir.
• Optoelektronik malzemelerin manyetik özellik göstermediklerini kabul ederek sadece elektrik
alandan kaynaklanan değişimler göz önünde bulundurulacaktır.
r r
• Dış elektrik alanla ortamın kutuplanmasından (P) dolayı oluşan net yükün ( ρind = ∇ .P) etkisini
E alanı yerine yeni tanımlayacağımız D vektörü ile ifade edeceğiz.
• Bu amaçla, ilk yapılacak iş ortamın kutuplanabilirliğini tanımlamak ve kutuplanabilirliği dış
elektrik alana bağlayacak eşitlik türetmek olacaktır.
7
Dipol Momentleri
Dış elektrik alanın ortamın elektrik özelliklerini nasıl değiştireceğini ortamdaki elektrik
dipollerini tanımlayarak anlatabiliriz.
Uygulanan dış alan madde içinde:
• İndüksiyon yolu ile elektrik dipoller oluşturur (atomun yük yoğunluğunun değişmesinden
kaynaklanan dipoller),
• Var olan dipolleri (dış alan olmadan da var olan dipollerin, örneğin su molekülünde
olduğu gibi) alan ile aynı doğrultuya getirmeye çalışır.
e
-Ze
e
+Ze
e
e
e
e
dipol moment tanımı
-q
p
+q
d
Aralarındaki mesafe d olan iki
zıt yükün dipol momenti (p)
p=qd
Enet
Eind
E=0
E
µ
+Ze
-Ze
E
E≠0
µatom=Bir atomun dipol momenti
µatom=(Ze)d
Dış elektrik alan atomun yük
yoğuluğunu değiştirerek dipol
momenti oluşmasını sağlar. 8
Kutuplanma Vektörü-1
Ortamın dış elektrik alana tepkisi ortamın kutuplanabilirliği ile ölçülür ve bu tepki
Kutuplanma Vektörü (Polarization Vector) ile ifade edilir.
Kutuplanma Vektörü (P)
r
P=
r
µ
∑ atom
V
şeklinde tanımlanır.
µatom=Bir atomun dipol momenti
V=Hacim
Kutuplanma Vektörü, vektörel bir nicelik olduğundan büyüklüğü ve yönü vardır:
Büyüklüğü (|P|): dipol moment/hacim
P=
Yönü: dipol momentin yönündedir.
Yoğunluğu ρ, atomik kütlesi A olan bir maddenin NA Avagadro sayısı olmak üzere
Kutuplanma vektörü (büyüklüğü)
r
N
P = ( A ρ)µ atom
A
şeklinde verilebilir.
Ortamın optik özelliklerinin bilinmesi açışından P ile E arasındaki ilişkinin bilinmesi gerekir
P ile E arasında nasıl bir ilişki vardır?
9
Kutuplanma Vektörü-2
Uygulanan dış elektrik alan (E) ile Kutuplanma Vektörü (P) arasında nasıl bir ilişki vardır?
Bu ilişki en genel olarak:
r r
r
r
r
r
(1)
(2) 2
(3) 3
P ( E ) = Po + ε o χ E + ε o χ E + ε o χ E + ...
şeklinde ifade edilebilir.
Burada Po , kalıcı kutuplanmadır (Dış elektrik alan olmadan var olan kutuplanma,
örneğin H2O molekülünde olduğu gibi) ve birçok malzeme için sıfırdır. Işığın
ortamda ilerleyişi söz konusu olduğundan dış elektrik alan ile oluşan değişim bizim
için önemli olduğundan bu terim ile ilgilenmeyeceğiz.
C+
O-
C+
O-
Po≠0
Po=0
H+
H+
χ ise elektrik duygunluk (electric susceptibility) ve madenin optik özelliklerini
incelemede oldukça önemli bir parametredir.
χ(1)= 1. dereceden elektrik duygunluk
χ(2)= 2. dereceden elektrik duygunluk (doğrusal olmayan optik)
Bu bölümde sadece elektrik alan ile orantılı olan doğrusal terim
r r
r
(1)
P(E) = εo χ E
ile ilgilenilecektir. Bölüm 11’de doğrusal olmayan terimler dikkate alınacaktır.
10
Kutuplanma Vektörü-3
P
E
r r
r
r
r
r
(1)
(2) 2
(3) 3
P ( E ) = Po + ε o χ E + ε o χ E + ε o χ E + ...
Kristal malzemeler yön özelliği gösterdiklerinden malzemenin elektrik
duygunluğu en genel durumda bir tensörle ifade edilir.
Böyle malzemelerde farklı yönlerde uygulanan aynı büyüklükteki
elektrik alana malzemenin tepkisi farklı olur ve E ve P vektörleri her
zaman birbirine paralel olmayabilir (Bölüm 8).
Bu durumda Kutuplanma Vektörü (P)
χ xx
Px
P = ε χ
y o yx
χ zx
Pz
χ xy
χ yy
χ zy
χ xz Ex
χ yz E y
χ zz Ez
x
z
y
χx≠χy≠χz
şeklinde ifade edilir. Tensörel ifadeden de görüleceği üzere kutuplanma vektörünün
bir bileşeni sadece elektrik alanın o yöndeki bileşeni cinsinden değil, diğer üç
bileşenin toplamı cinsinden ifade edilecektir.
Bu derste sadece izotropik malzemeler (yön özelliği olmayan malzemeler) ile
11
ilgilenilecektir, anizotropik malzemeler 8. Bölümde incelenecektir.
Optik Ortamlar
Elektrik duygunluk (χ) ortamın optik özelliğini
yansıttığından duygunluk ifadesini göz önünde
bulundurarak ortamı optik olarak sınıflandırabiliriz.
r r
r
r
r
r
(1)
(2) 2
(3) 3
P ( E ) = Po + ε o χ E + ε o χ E + ε o χ E + ...
(a) Homojen (Homogenous)
(b) İzotropik (İsotropic)
x
x
χ=sabit
χ(r)
y
y
homojen ortam
x
inhomojen ortam
x
χx=χy=χz=sbt
χx=sbt≠χy=sbt
y
≠χz
y
izotropik ortam
anizotropik ortam
x
(c) Dağıtkan (Dispersive)
x
v(ω)=sabit
(d) Doğrusal (Nonlinear)
v(ω)
y
dağıtgan olmayan ortam
x
y
dağıtgan ortam
x
PαE
doğrusal ortam
y
P α E2
12
y
doğrusal olmayan ortam
Elektrik Yerdeğiştirme Vektörü
Elektrik Yerdeğiştirme Vektörü (D)
Ortamın, dış elektrik alandan dolayı kutuplanmasını içerecek yeni bir vektör,
Elektrik Yerdeğiştirme Vektörü (D) tanımlanabilir.
Ortamın elektriksel özelliklerini içeren bu yeni vektör Maxwell denklemlerinde kullanılırsa
ortamın kutuplanma etkisi dalga denklemine yansıtılmış olur.
E ve P cinsinden yer değiştirme vektörü D
r
r r
D = ε o (E + P)
şeklinde tanımlanır. P’yi elektrik alan cinsinden (1. dereceden katkı alınarak) ifade edersek
r r
r
(1)
P( E ) = ε o χ E
E cinsinden D yerdeğiştirme vektörü
r
r
r
r
r
r
(1)
(1)
D = ε o ( E + χ E ) ⇒ D = (ε o + ε o χ )E = ε E
ε ≡ ε o (1 + χ (1) )
Ortamın elektrik geçirgenliği
13
Dielektrik Ortam-1
r
r
D =εE
ε ≡ ε o (1 + χ (1) )
Ortamın elektrik geçirgenliği
D vektörü, madde ortamında toplam (net) elektrik akısıdır.
Elektrik alan için yapılan benzer işlemler manyetik alan için de yapılabilir.
Elektrik Özellikler
E => D (D=εoE+P =>D=εE)
εo => ε
D=Elektrik yerdeğiştirme
Manyetik Özellikler
H => B (B=µoH+µoM => B=µH)
µo => µ
B=Manyetik akı
Madde ortamının özelliğini iki sabit, µ ve ε belirler. Bu ders kapsamında
ilgileneceğimiz optik malzemeler manyetik özellik göstermedikleri için µ≈µ0
olarak alınabilir; dolayısı ile sadece ε’nin özellikleri ile ilgileneceğiz.
Boşluk
r
2
r
∂ E
∇ 2 E = εo µo 2
∂t
( µ ≈ µo )
( εo→ε )
Madde ortamı
r
2
r
∂ E
∇ 2 E = εµo 2
∂t
Ortamı karakterize eden elektrik geçirgenlik ε, Maxwell denklemlerinde yerine
konularak madde ortamı için dalga denklemi elde edilir.
14
Dielektrik Ortam-2
r
2
r
∂ E
∇ 2 E = µo ε 2
∂t
vortam
Madde Ortamında Dalga Denklemi
1
1
≡ vm =
≅
<c
µε
µ 0ε
Dalga denkleminin çözümü :
r r
r r
r
E (r , t ) = Eo sin(km .r − ωt + φ )
r r
r r
r
H (r , t ) = H o sin(km .r − ωt + φ )
Elektrik alan
Manyetik alan
km: madde ortamında dalga vektörü
Madde ortamında ışığın hızı değiştiğinden dalga boyu dolayısı ile dalga vektörü
de değişime uğramıştır.
λm .ν = vm
15
Kırılma İndisi-1
Işığın madde ortamındaki hızı (vm) boş uzaydaki hızı (c) ile karşılaştırılabilir. Bu hız,
dalganın madde ortamındaki davranışına ilişkin birçok ifadede yer aldığı için
önemlidir.
Boş uzaydaki ışık hızı: c =
1
ε oµ 0
Kırılma indisi (n) tanımı
Madde ortamında ışık hızı: vm =
(
n≡
1
µ oε o
1
µ0ε
)
c
ε
=
=
vm ( 1 )
εo
µ oε
Kırılma indisi, ışığın boşluktaki hızının (c), madde içindeki hızına (vm) oranıdır.
Örneğin, kırılma indisi n=4.0 olan bir ortamda ışık, boşluktaki yayılma hızının
¼ katı hızda ilerleyecektir.
Kullanışlı bir başka tanım ise dielektrik sabitidir.
ε
= n2
Dielektrik sabiti (κ) tanımı: κ ≡
εo
16
Gerçekte ε ve κ frekansa bağlıdır ama şimdilik incelemelerimizde bunu göz ardı edeceğiz
Kırılma İndisi-2
Optoelektronik teknolojisinde yaygın olarak kullanılan bazı malzemelerin kırılma indisi
değerleri (Kırılma indisi frekansa çok sıkı bağlıdır, bu bağlılık Bölüm 6’da ayrıntılı olarak
incelenecektir.)
Madde
Kırılma İndisi
n≡
c
=
vm
ε εo
Boşluk
1,0000
Hava
1,0003
Su
1,333
Cam
1,5-1,7
Si
3,5
Ge
4,0
GaAs
3,6
AlAs
3,2
InP
3,5
InAs
3,8
InSb
4,2
17
Kırılma İndisi-3
Bu sonuca göre dielektrik ortamda ilerleyen dalganın dalga parametreleri kırılma indisi
ile orantılı olarak değişikliğe uğrayacaktır.
c
≡n
vm
ω
vm =
km
λo
n
Dalgaboyu
λm =
Açısal frekans
ωm = ωo = 2πv
(Azalır)
(Değişmez!)
2π
2π
=n
= nko (Artar)
λm
λo
Dielektrik durum için dalga denkleminin çözümleri (+z yönünde ilerleyen dalga için)
r
r
E ( z , t ) = Eo sin(km .z − ωt + φ )
λ m ν = vm
km =
Dalga vektörü
E(z)
ko
E(t)
c
ω
ω
v
z
t
km
Boş uzay z=0
λo
dielektrik
λm = λo n
Dalgaboyu, madde ortamında
kırılma indisi (n) kadar azalmıştır
Boş uzay
z=0 dielektrik
ωo = ωm
Açısal frekans iki
ortamda da aynı
18
İletken Ortam-1
Durum II: J ≠ 0 (İletken ortam, ρserbest=0)
İletkenlerde (örneğin altın, alüminyum, gümüş) serbest taşıyıcılar oldukça fazladır >1026 m-3
Maxwell Denklemleri:
r r
(1) ∇ .D = 0
r r
(2) ∇ .H = 0
r
r r
∂H
(3) ∇ × E = − µo
r∂t
r r
r
(4) ∇ × H = ε o ∂E + J
∂t
Bağlı elektronların (dipollerden gelen katkı) etkisi yani, kutuplanma etkisi, D alanı içindedir.
Bunun yanı sıra serbest elektronlardan gelecek katkı akım yoğunluğu (J) teriminin içindedir.
Yukarıdaki Maxwell denklemlerini çözebilmek için J ile uygulanan dış elektrik alan E
arasında bir ilişki türetmemiz gerekecektir.
Eğer işlemlerimizi doğrusal malzemelere (Ohm yasasına uyan malzemeler) sınırlandırırsak J
ile E arasındaki ilişki
r
r
J =σE
(Ohm yasası)
şeklinde yazılır. Burada σ iletkenliktir, ve öz direncin (ρ) tersi olarak tanımlanır (ρ=1/σ).
r
Bu durumda 4. Maxwell eşitliği:
r r
r
∂E
19
∇ × H = εo
+σ E
∂t
İletken Ortam-2
İletken ortamda Maxwell Denklemleri:
r r
(1) ∇ .D = 0
r r
(2) ∇ .H = 0
r
r r
∂H
(3) ∇ × E = − µo
r∂t
r r
∂E r
(4) ∇ × H = ε o
+J
∂t
r
r r
r
∂E
∇ × H = εo
+σ E
∂t
Boş uzay ve dielektrik ortamda yapılan işler tekrarlanırsa yukarıdaki denklemlerin çözümü
olacak elektrik alanın
r
r
2
r
∂ E
∂E
∇ 2 E = µoε 2 + µoσ
∂t
∂t
İletken ortamda dalga denklemi
(Manyetik alan için de benzer bir ifade yazılabilir)
şeklinde dalga denklemini sağlayacağı gösterilebilir. Görüldüğü gibi bu ifade, boş uzay ve
dielektrik ortamdaki dalga denklemine benzemesine rağmen iletkenlik ifadesini içeren
fazladan bir terim daha içermektedir.
Yukarıdaki dalga denklemi, ikinci dereceden kısmi diferansiyel denklemdir ve çözümleri
bilinmektedir.
20
İletken Ortam-3
Bu iki denklemi metal ortam için yeniden çözmek yerine, dielektrik ortam için
bulduğumuz çözümlere benzeterek iletken ortam için çözümler elde edebiliriz.
Dalga denkleminin metal ortamda çözümlerinin
r
r i ( kr .rr −ωt +φ )
E (r , t ) = Eo e m
r
r i ( kr .rr −ωt +φ )
H (r , t ) = H o e m
şeklinde olduğunu varsayabiliriz.
Bu çözümleri Maxwell denklemlerinde kullandığımızda aranan dalga vektörleri
(km) Maxwell denklemleri yardımı ile bulunabilir.
Dielektrik
r r
r
∇ × E = +iωH
r r
r
∇ × H = ε(−iω) E
İletken
r r
r
∇ × E = +iωH
r r
r
r
∇ × H = σE + ε(−iω) E
21
İletken Ortam-4
Dielektrik
İletken
r r
r
∇ × H = ε(−iω) E
r r σ
r
∇× H =
+ ε (−iω) E
−
ω
(
i
)
r r
Dielektrik ve iletken ortam için ∇× H denklemleri karşılaştırıldığında;
iletken ortamı temsil edecek karmaşık
bulunan çözümleri kullanabiliriz.
r r σ
r
∇× H =
+ ε (−iω) E
(−iω)
ε̂ tanımı yapılarak dielektrik ortam için
r r
r
ˆ
∇ × H = ε(−iω) E
Burada
σ
σ
εˆ ≡
+ε = ε+i
−iω
ω
Bu durumda karmaşık elektrik geçirgenlik cinsinden dalga denklemi
r
2
r
∂ E
∇ 2 E = µo εˆ 2
∂t
İletken ortamda dalga denklemi
ε karmaşık sayı!
Işığın (iletken içinde) hızı viletken =
ω
kiletken
=
1
µoεˆ
22
İletken Ortam-5
εˆ ≡ ε + i
Kırılma indisi tanımı hatırlanırsa n =
ε
εo
=>
σ
ω
nˆ =
εˆ
εo
Kırılma indisi de (bu durumda) karmaşık sayıdır!
n̂ = n + iK
Karmaşık Kırılma İndisi (iletken ortam)
n=Kırılma indisi (Gerçek Kısım)
K=Yoketme indisi (Sanal Kısım)
Dalga Vektörü
ω
kˆm = nˆ
c
ω
kˆm = (n + iK )
c
Karmaşık Dalga Vektörü (iletken ortam)
ω
n Dalga vektörü (gerçek)
c
ω
Im( kˆm ) = K Dalga vektörü (sanal)
c
Re( kˆm ) =
En genel durumda kırılma indisinin karmaşık bir nicelik olduğu, dolayısı ile ortamın
23
optik özelliklerini gerçek (n) ve sanal (K) sabitlerin belirlediği söylenebilir.
İletken Ortam-6
Karmaşık kırılma indisi fiziksel olarak ne anlama gelir?
Bunun için karmaşık dalga vektörünü dalga çözümünde kullanalım
ω
ˆ
n̂ = n + iK
kˆm =
ω
c
Re(k m ) =
(n + iK )
+z yönünde ilerleyen ışığı düşünelim
Im(kˆm ) =
c
ω
c
n
K
r
r i ( k .z −ωt +φ )
E(z,t)= Eo e m
Karmaşık km ifadesi bu çözümde kullanıldığında
i.i=-1
r
r i ( ωc nz +i ωc kz ) −ωt +φ
E(z,t)= Eo e
r
r − ω Kz i ωc nz −ωt +φ
E(z,t)= Eo e c e
ω
i nz −ωt +φ
r
r − ω Kz i ωc nz −ωt +φ
E(z,t) = Eo e c e
= E ( z )e c
İletken Ortamda
Elektrik Alan
Bu ifadede iki terim bulunmaktadır
Birinci terim genlik ifadesidir ve kırılma
İkinci terim, salınım yapan terimdir; bu
indisinin sanal teriminden (yoketme
ifade içinde kırılma indisinin gerçek kısmı
indisi) dolayı üstel olarak (z ile)
bulunmaktadır ve dalganın ortamda
azalmaktadır. Bu azalmadan serbest
yayılma özelliğini (z ile) belirler;
yükler sorumludur.
n̂ = n + iK dielektrik ortamda bulunan sonuç gibidir.
24
c / vm = n
K ∝ soğurma
İletken Ortam-7
Elektrik alanın genliği, z değerine bağlı olarak azalarak sıfıra gitmektedir.
ω
i nz −ωt +φ
r
r − ω Kz i ωc nz −ωt +φ
E(z,t) = Eo e c e
= E ( z )e c
İletken ortamda
elektrik alan
Ortamdaki enerji akısına yani Parlaklığa (Poynting vektörün zaman ortalaması) bakalım
r
r2
S = I = ε oc E
Parlaklık
Elektrik alanın karesinin zaman ortalaması alınırsa
r 2 −2( ω Kz )
I(z) = εvm Eo e c = I o e −αz
Burada
Kayıp ortamı
α>0, I<Io
Io
α
I
z
α≡
İletken ortamda
parlaklık
2ω
K soğurma katsayısı (1/uzunluk)
c
Soğurma katsayısı α, ölçülebilir bir nicelik olup
birim uzunluk başına (pratikte cm-1) soğurma
miktarıdır. Kayıplı ortamda α pozitif değere sahip
olmasına rağmen kazanç ortamında (lazer kovuğu)
negatif işarete sahiptir.
Kazanç ortamı
α<0, I>Io
Io
α
I
25
z
Madde Ortamında Işık
Boşluktan iletken bir ortama giren ışığın genliği, yoketme indisinin (K) sıfırdan farklı (ve
pozitif) olmasından dolayı azalır (soğrulur). Dielektik ortamda yoketme indisi sıfır olduğu
için genlikte bir azalma (soğrulma) olmaz.
E(z,t)
E(z,t)
z
z
Boş uzay z=0 iletken
Boş uzay z=0 dielektrik
ω
i nz −ωt +φ
r
E(z,t)= E ( z )e c
ω
i nz −ωt +φ
r
c
E(z,t)= e
I(z)
I(z)
Eo/e
z
δ
Boş uzay z=0 dielektrik
I(z)= I o
Boş uzay z=0 iletken
I(z) = I o e −αz
Genliğin e-1değerine
düştüğü z değerine
z (δ) “sızma derinliği
(penetration dept) ”
denir.
e-1=1/2.7≈1/3
Bakır (morötesi λo=100 nm) δ=0.6 nm26
(kızılaltı λo=10 000 nm) δ=6 nm
Maddenin Optik Sabitleri
Ortamın optik özelliğini karmaşık kırılma indisi verir (hem soğurmayı (yoketme indisi)
hem de dalganın ilerleyişini (kırılma indisi) karakterize eden nicelikleri barındırdığı için)
ω
km = n
c
r
r i ( ω nz −ωt +φ )
E(z,t)= Eo e c
ω
kˆm = (n + iK )
c
r
r i ( ωc nz +i ωc kz ) −ωt +φ İletken (σ≠0)
E(z,t)= Eo e
2ω
α≡
K
I(z) = I o e −αz
Parlaklık
Dielektrik (σ=0)
c
• Eğer bir ortamda dipollere ek olarak serbest taşıyıcılar da var ise ortamın kırılma
indisinin karmaşık bir sayı ile ifade edilmesi gerekecektir. Bu durumda kırılma
indisinin gerçek kısmı dalganın ortamdaki ilerlemesini, sanal kısmı (yoketme
indisi) ise ortamda soğrulmasını göstermektedir.
• Kırılma indisinin hem gerçek hem de sanal kısımları frekansa çok sıkı bağlıdır.
Belli bir dalga boyunda geçirgen olan (sanal kırılma indisi sıfır) başka bir
dalgaboyunda çok iyi bir soğurucu olabilir.
• Bazı durumlarda ise kırılma indisi tümüyle sanal olabilir (Bölüm 6). Bu durumda
ortam mükemmel ayna gibi davranır ve ortamda ilerleyen dalga bulunmaz, ara
yüzeye gelen ışık tümüyle yüzeyden geri yansır.
27
Boş Uzay
ρ=0
J=0
P=0
r
r r
∂H
∇ × E = − µo
∂t
r
r r
∂E
∇ × H = εo
∂t
r r
∇ .E = 0
r r
∇ .H = 0
Dielektrik Ortam J=0
ε o , µo
r
r
D ≡ ε oE
ρ=0
J=0
P≠0
P=εoχEo
r r
∇ .D = 0
r r
∇ .H = 0
c = νλ
n=
ω
km =
c
1
µ0ε o
c=
r
r r
r
D ≡ ε o E + P = ε E
ω
c
n=
1
µ0ε
vm =
E(z,t)
z=0
Boş uzay
λm < λ
ωm = ωo
λm < λ
ωm = ωo
z
z
z
Boş uzay
r
r − ω Kz
ω
E (z, t) = Eo e c sin( nz − ωt + φ )
c
E(z,t)
λo
ω0
1
µ 0ˆε
r
r ˆ
E ( z , t ) = Eo ei ( km z −ωt +φ )
r
r
ω
E (z, t) = Eo sin( nz − ωt + φ )
c
r
r
ω
E (z, t) = Eo sin( z − ωt + φ )
c
c
εˆ
=
>1
vm ε o
ω
kˆm = (n + iK )
c
n = ko n
r
r
E ( z , t ) = Eo ei ( km z −ωt +φ )
r
r
E ( z , t ) = Eo ei ( ko z −ωt +φ )
r
r r
∂H
∇ × E = − µo
∂t r
r r r
∂E
∇ × H = J + εo
∂t
r r
∇ .D = 0
r r
∇ .H = 0
vm = νλ m
c
>1
vm
vm =
E(z,t)
ε , µo
vm = νλ m
c c
n = = =1
v c
ko =
r
r r
∂H
∇ × E = − µo
r∂t
r r
∂E
∇ × H = εo
∂t
Metalik Ortam J≠0
ρ=0
J≠0
J=σE
P≠0
P=εoχE
εˆ, µo
Boş uzay
z=0
dielektrik
Boş uzay
z=0 iletken
28
Özet
Madde ortamında ışığın hızı
vm =
1
µ oε
(
Kırılma indisi tanımı
n≡
1
)
µ oε o
c
ε
=
=
vm ( 1 )
εo
µ oε
Dielektrik sabiti
κ≡
ε
= n2
εo
Kırılma indisi cinsinde madde ortamında ışığın hızı
v=
c
n
Kırılma indisi en genel durumda karmaşık bir sayıdır: n̂ = n + iK
Gerçek kısmı => n=Kırılma indisi
Sanal kısmı => Κ=Yoketme (extinction) indisi
Kırılma indisinin gerçek kısmı (n) ışığın madde ortamında ilerleme hızını, sanal kısmı
(K) ise ışığın ortam tarafından soğrulmasını ifade eder.
29
UADMK - Açık Lisans Bilgisi
Bu ders malzemesi öğrenme ve öğretme yapanlar tarafından açık lisans
kapsamında ücretsiz olarak kullanılabilir. Açık lisans bilgisi bölümü yani bu
bölümdeki, bilgilerde değiştirme ve silme yapılmadan kullanım ve geliştirme
gerçekleştirilmelidir. İçerikte geliştirme değiştirme yapıldığı takdirde katkılar
bölümüne sadece ekleme yapılabilir. Açık lisans kapsamındaki malzemeler
doğrudan ya da türevleri kullanılarak gelir getirici faaliyetlerde bulunulamaz.
Belirtilen kapsam dışındaki kullanım açık lisans tanımına aykırı olduğundan
kullanım yasadışı olarak kabul edilir, ilgili açık lisans sahiplerinin ve kamunun
tazminat hakkı doğması söz konusudur.
30








