TEŞEKKÜR
Bu projeyi hazırlamamızda bize yardımcı olan
fizik öğretmenimiz Olcay
Nalbantoğlu’na ve çalışmalarımızda bize tüm olanaklarını sunan okulumuza teşekkür
ederiz.
GİRİŞ
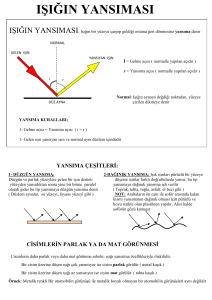
Işık ışınları bir ortamdan başka bir ortama geçerken yolunu değiştirebilir.
Şekil-I
İki ortamın kırılma indisine bağlı olarak ışık ışınları 5 farklı şekilde yollarına devem
ederler. Eğer 2. ortam 1. ortamdan yoğunsa (n > n ); ışın normale yaklaşarak
kırılacaktır (ışın V). Eğer her iki ortamın da kırılma indisi eşitse (n = n )
Işın kırılmadan yoluna devam eder (ışın IV). Eğer 1. ortam 2. ortamdan yoğunsa ışık
ya normalden uzaklaşarak (ışın III) kırılır ya tam yansıma yapar (ışın I) ya da sınır
açısıyla geliyorsa ayırma yüzeyinden geçecek şekilde kırılır (ışın II). Bu durum gelme
açısı ile sınır açısına bağlıdır.
Sınır açısı, ışının normalle dik açı yapacak şekilde kırıldığındaki gelme açısıdır. Snell
yasasına göre:
n . Sina=n . Sinb
a: gelme açısı (normal ile gelen ışın arasındaki açı)
b: kırılma açısı (normal ile kırılan ışın arasındaki açı)
Sınır açısını bulmak için kırılan ışığın normalle yaptığı açı 90 alınırsa:
Sinx=n /n (x sınır açısı)
Sınır açısından daha büyük açılarla gelen ışınlar diğer ortama geçemez. (Bu durum
sadece ışık çok yoğun ortamdan az yoğun ortama geçerken gözlenebilir.)
Kırılan veya yansıyan ışınlar Tablo-1’deki gibidir:
DURUM
IŞIN
n >n (gelme açısı>sınır açısı)
I
n >n (gelme açısı=sınır açısı)
II
n >n (gelme açısı<sınır açısı)
III
n =n
IV
n <n
V
Tablo-1
Bu proje değişik sıvıların, ışığı kırma indisini ölçmek için yapılmıştır. Kırıcılık indisi
maddelerin ayırt edici özelliklerindendir. Yine kırılma indisinden çözeltilerin
yoğunlukları hesaplanabilir.
Daha kesin sonuçlar elde edebilmek için farklı iki deney yapılmıştır. Birinci deneyde
çukur ayna kullanılırken, ikinci deneyde yarım daire şeklinde plastik bir kap
kullanılmıştır. Deneyler birçok defada yapılmış ve sonuçların ortalaması indisin
hesaplanmasında kullanılmıştır.
DENEY 1
ÇUKUR AYNA İLE KIRILMA İNDİSİNİN BULUNMASI
İlk önce çukur aynanın merkezi (eğrilik yarıçapı) Şekil-2’de görüldüğü gibi saptandı.
Daha sonra çukur ayna yüzeyi, indisi ölçülecek sıvı ile dolduruldu. (Şekil-3)
ŞEKİL-4
DENEY SONUÇLARI
R=20,5 için:
SIVI
Su
Etil alkol
Gliserin
BaCl çözeltisi
h (cm)
16,0
15,8
13,4
14,6
Tablo-2
İndis
1,28
1,30
1,53
1,40
DENEY 2
LAZER İLE KIRILMA İNDİSİNİN ÖLÇÜLMESİ
Yarım daire şeklindeki plastik kabın içi, indisi ölçülecek sıvı ile dolduruldu. Daha
sonra 10° ve 30° lik açılarla plastik kabın O noktasına lazer ışını yollandı. Işının (dik
gelmediği sürece) tamamı diğer ortama geçemediğinden yansıyan ışın (gelme
açısı=yansıma açısı kullanılarak) için de bir çizgi çizildi. Kırmızı lazer ışığı çizilen bu
iki çizgi ile aynı doğrultuda olduğu zaman kırılan ışığın normal ile yaptığı açı ölçüldü.
Plastik kabın ışığı kırması ihmal edildi.
SEKİL-5
30 Gelme Açısı İçin
SIVI
θ SIVI
İndis
Su
21
1,39
Etil alkol
21,5
1,36
Gliserin
20,1
1,45
BaCl
22,1
1,32
Tablo-3
10 Gelme Açısı için
θsıvı
Su
7,6
İndis
1,31
Etil alkol
7,9
1,26
Gliserin
6,6
1,51
BaCl çözeltisi(derişik)
7,3
1,36
Tablo-4
Sıvının içinden dışarıya (havaya) bakan bir gözlemciye göre , C deki bir noktasal cismi
(düzlem kırıcı yüzeydeki kırılmalardan dolayı) M de görmesi durumu ile eşdeğer bir
durumdur.
Dolayısıyla C “cisim” , M “görüntü” rolü oynamak üzere :
İlişkisi bu duruma uyarlanırsa
= 1 ve Dcisim
h
=n ve Dgörüntü
r olmak üzere 1/h = n/r ilişkisinden n=r/h
bulunur.
Burada hata yüzdesi: ∆n/n x 100%= (∆r/r + ∆h/h) x 100% çerçevesinde:
I
II
III
r ve h ın ölçülmesinde , sıvının ihmal ettiğimiz derinliğinden,
Cisim görüntü çakıştırmasından ki bu da r ve h’ nin belirlenişindeki hata
olasılığıdır,
Sıvı yüzeyinin düzlem sayılması ki bu da r ve h ölçümünde ve O kırılma
noktasında Snell yasası uygulamasında hataya yol açar.(Oysa, özellikte ayna
kenarlarına yaklaştıkça sıvı yüzeyi eğriselleşmektedir)
DENEY-2 Sonuçları:
sıvı
su
Etil alkol
Gliserin
BaCl
çözeltisi
Ortalama İndis
1,35
1,31
1,48
1,34
DEĞERLENDİRME
Yapılan deneylerin eşit ağırlıklı sonuçları ve gerçek değerler Tablo-4’teki gibidir:
sıvı
su
etil alkol
gliserin
BaCl2
çözeltisi
Deney-1
indisi
1,28
1,3
1,53
1,40
deney-2 indisi
1,35
1,31
1,48
1,34
TABLO-4
ortalama
indis
1,31
1,3
1,5
1,37
gerçek değer
1,33
1,36
1,47
1,35
hata oranı
(%)
1,2
2,2
2
1,4
Görüldüğü gibi kırılma indisi sıvının yoğunluğuna ve akışkanlığına bağlıdır. Genellikle
yoğunluk arttıkça indis artmaktadır.
Çözeltilerin derişimleri kırılma indisini etkilemektedir. Derişim arttıkça indis de
artmaktadır.
Hata payları ölçüm aletlerinin çok hassas olmamasından, lazer ışığının kalınlığından,
ayna üzerine konulan sıvı yüzeyinin düz olmamasından ve ayna ile sıvı arasındaki
uzaklığın ihmal edilmesinden kaynaklanmaktadır.
KAYNAKÇA:
Hanbook of Elementary, MIR, 1980