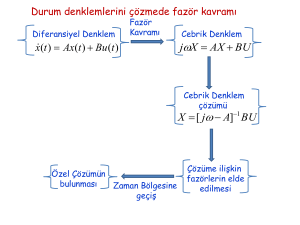
Hatırlatma
Elektrik Devrelerinin Temelleri dersinde ne yapacağız?
Amaç: Fiziksel devrelerin elektriksel davranışlarını öngörme
akım ve gerilim
Teori oluşturken işe nasıl başlarız?
Tanımlanmamış büyüklükler
Aksiyomlar
Sonra ne yaparız?
Yeni büyüklükler için: Tanımlar
Yeni sonuçlar için: Teoremler
Hatırlatma
Elektrik Devre Teorisi
Tanımlanmamış büyüklükler
Akım
i(t) [A]
uyumlu çift
1
+
v1 (t)
2
_
İ1 (t)
Gerilim
v(t) [V]
Hatırlatma
Aksiyomlar
Ne demek?
1. Toplu Parametreli Devre
Fiziksel devrede her aletin uçlarındaki akım i(t) ve gerilim v(t)
her t anında tam olarak tanımlanmışsa, devre toplu parametreli devredir.
Kirchhoff’un Gerilim Yasası (1845)
Önce biraz hazırlık
• n düğümü olan toplu parametreli, birleşik bir devrede
herhangi bir düğümü referans düğümü olarak seç.
• seçilen referans düğümüme göre n-1 tane düğüm gerilimi
tanımla
1
+
3
+
+
e1 e2
e3
. . . k
+.
ek
__ _
__
en=0 n
Vkn-1
2
. .
+
en-1
• k. düğüm ile j. düğüm
arasındaki gerilim farkı: vkj
n-1
Hatırlatma
2. Kirchhoff’un Gerilim Yasası (KGY)
Tüm toplu parametreli birleşik devrelerde referans düğümü keyfi
seçilmek üzere tüm k, j düğüm çiftleri için, her t anında
vkj (t ) ek (t ) e j (t )
bağıntısı geçerlidir.
2. Kirchhoff’un Gerilim Yasası (KGY)
Tüm toplu parametreli birleşik devrelerde tüm kapalı düğüm
dizileri için, her t seçilen kapalı bir düğüm dizisi için düğümden
düğüme gerilimlerin cebirsel toplamı sıfırdır.
Teorem:
Düğüm gerilimleri cinsinden
KGY
Kapalı düğüm dizileri cinsinden
KGY
Hatırlatma
Kirchhoff’un Akım Yasası (KAY)
+
_
Gauss Yüzeyi
içi ve dışı tanımlı, sadece devre elemanlarını
birleştiren bağlantıları kesecek şekilde çizilmiş
yüzey
3. Kirchhoff’un Akım Yasası (KAY)
Tüm toplu parametreli devrelerde, tüm Gauss yüzeyleri için her t
anında Gauss yüzeyini kesen akımların cebirsel toplamı sıfırdır.
3. Kirchhoff’un Akım Yasası (KAY) (Düğümler için)
Tüm toplu parametreli birleşik devrelerde, her t anında, herhangi
bir düğümden çıkan akımların cebirsel toplamı sıfırdır.
KAY ve KGY toplu parametreli devrelerde geçerli
KAY ve KGY elemanların özelliklerinden bağımsız
KAY ve KGY ile elde edilen denklemler katsayıları 1,-1,0 olan lineer
lineer, cebrik, homojen denklemler
Örnek
2
1
5
6
3
7
4
8
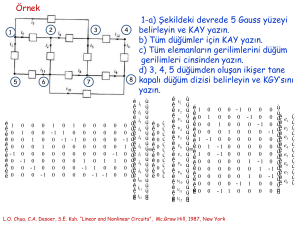
1-a) Şekildeki devrede 5 Gauss yüzeyi
belirleyin ve KAY yazın.
b) Tüm düğümler için KAY yazın.
c) Tüm elemanların gerilimlerini düğüm
gerilimleri cinsinden yazın.
d) 3, 4, 5 düğümden oluşan ikişer tane
kapalı düğüm dizisi belirleyin ve KGY’sını
yazın.
L.O. Chua, C.A. Desoer, S.E. Kuh. “Linear and Nonlinear Circuits”, Mc.Graw Hill, 1987, New York
Graf Teorisi
Pregel Nehri
http://en.wikipedia.org/wiki/Leonhard_Euler
Leonard Euler (1707-1783)
1736’da Königsberg’in yedi köprüsü problemini graf teorisinden
yararlanarak çözdü
Bir graf nasıl tanımlanır?
G {V , E}
düğüm
kümesi
çizgi
kümesi
1
1
2
2
9
7
6
8
3
3
6
4
4
Elektrik devrelerine ilişkin çizeceğimiz
graflarda çizgi yönlüdür
5
5
GD VD , ED 1,2,3,4,5,6 , 1,2,3,4,5,6,7,8,9
2-uçlu elemana ilişkin uç-grafı
1
+
1
İ1 (t)
Sadece ok yeterli,
neden?
v1 (t)
2
_
2
Tanım: (Ani Güç)
p(t ) ˆ v(t )i (t )
[Watt] [Volt] [Amper]
Ani güç, t anında elemanın bağlı olduğu devre tarafından elemana
aktarılan güç
3-uçlu elemana ilişkin uç-grafı
_
1
+
V21
İ1 (t)
İ2 (t)
3- uçlu
eleman
+_
1
2
2
3
1
2
3
İ3 (t)
_
+
1
2
3
Hangisini, nasıl seçeceğiz?
3
Referans nerede?
1
+
İ1 (t)
İ2 (t)
3- uçlu
eleman
+
2
1
2
İ1 (t)
İ2 (t)
_ _
3
Referans 3 düğümü
3
Referans nerede?
1
+
_
V1
İ1 (t)
3- uçlu
eleman
_
2
1
İ1 (t)
2
İ3 (t)
İ3 (t)
+
3
Referans 2 düğümü
3
Referans nerede?
_
1
V2
İ2 (t)
_
+
2
İ2 (t)
1
2
3- uçlu
eleman
İ3 (t)
+
İ3 (t)
3
Referans 1 düğümü
3
Bu graf gösterimleri ile birşeyler kayboldu, neler?
Kaybolanları nasıl bulacağız?
_
1
+
V21
İ1 (t)
İ2 (t)
3- uçlu
eleman
+_
G1
2
2
1
3
2
Kapalı düğüm dizisi için KGY
yazalım
v21(t ) v13 (t ) v32 (t ) 0
G1 Gauss yüzeyi için KAY
yazalım
İ3 (t)
_
+
3
i1 (t ) i2 (t ) i3 (t ) 0
n-uçlu elemana ilişkin uç-grafı
2
1
İ1 (t)
İ2 (t)
İk(t)
k
1
n- uçlu
eleman
İ1 (t)
2
k
İk(t)
İ2 (t)
İn-1 (t)
İn-1(t)
n
n
n-1
Tanım: (Ani Güç)
n 1
p(t ) ˆ vk (t )ik (t )
k 1
n-1
2-kapılılar, çok kapılılar
S1 Gauss yüzeyi için KAY yazalım:
i1 (t ) i1' (t ) 0
S2 Gauss yüzeyi için KAY yazalım: i2 (t ) i2' (t ) 0
i1 (t ) i1' (t )
i2 (t ) i2' (t )
2-kapılıya ilişkin uç-grafı
Tanım: (Ani Güç)
p(t ) ˆ v1 (t )i1 (t ) v2 (t )i2 (t )
L.O. Chua, C.A. Desoer, S.E. Kuh. “Linear and Nonlinear Circuits”, Mc.Graw Hill, 1987, New York
2- kapılı eleman içeren devre ayrık olmaz mı?
S1 Gauss yüzeyi için KAY yazalım:
ik (t ) 0
S1
Devre grafı: Verilen bir devre için devredeki her elemana ilişkin uç grafı
çizilerek elde edilen grafa devre grafı denir.
L.O. Chua, C.A. Desoer, S.E. Kuh. “Linear and Nonlinear Circuits”, Mc.Graw Hill, 1987, New York
Örnek
L.O. Chua, C.A. Desoer, S.E. Kuh. “Linear and Nonlinear Circuits”, Mc.Graw Hill, 1987, New York
GrafTeorisine İlişkin Bazı Tanımlar
Tanım: (Derece)
Bir düğüme bağlı eleman sayısına o düğümün derecesi denir.
Tanım: (Yol)
G grafının aşağıdaki özellikleri sağlayan Gy alt grafına yol denir:
• Gy ‘nin n çizgisi, n+1 düğümü vardır.
• Gy ‘deki çizgiler e1, e2, ...,en düğümler d1,d2, ....,dn+1 olmak
üzere sırasıyla öyle numaralanabilirler ki ek çizgisinin düğümleri
dk ve dk+1 olur.
• d1 ve dn+1 düğümlerinin dereceleri bir diğer düğümlerin dereceleri
ikidir.
Tanım: (Birleşik Graf)
Verilen G grafında herhangi iki düğüm arasında en az bir yol
varsa buna birleşik graf denir.
Tanım: (Çevre)
G grafının aşağıdaki özellikleri sağlayan Ga alt grafına çevre denir:
• Ga birleşik bir graftır.
• Ga ‘daki bütün düğümlerin dereceleri ikidir.
Tanım: (Ağaç)
Birleşik bir G grafının aşağıdaki özellikleri sağlayan GT alt grafına
ağaç denir:
• GT , G’nin tüm düğümlerini kapsar.
• GT çevre içermez.
Tanım: (Dal)
Ağaç’ın elemanlarına dal denir.
Tanım: (Kiriş)
G grafından GT çıkarıldığında geriye kalan alt grafa kirişler kümesi
denir.
Sonuç: nd düğümlü bir G grafında seçilecek dal sayısı nd-1 dir.