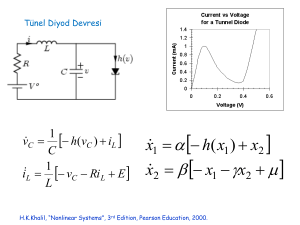
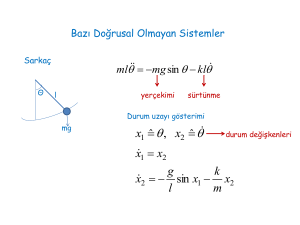
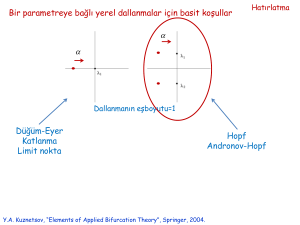
2. Mertebeden Diferansiyel Denklemlerin Çözümü
x1 a11
x a
2 21
a12 x1 b1
u ,
a22 x2 b2
x Ax Bu ,
x(t0 ) x0
x(t0 ) x0
Çözüm, 1. mertebeden diferansiyel denklemlerin çözümlerine benzer
şekilde
x (t ) x (t ) x (t )
T
h
özel
Homojen kısım: x
Ax,
xh (t ) Set
x(t0 ) x0
S1 t
e
S2
Set ASet
S AS
I AS 0
detI A 0
Çözüm Tahmini
belirlememiz gereken kaç
büyüklük var?
sıfırdan farklı çözüm erin
olması nasıl mümkün olur?
2 a b 0
Karakteristik
Denklem
Karakteristik denklemin kökleri:
1, 2 özdeğerler
Belirlememiz gereken S özvektör
Hangi uzayın elemanı?
O uzaya ait neyi belirlersek
aradığımızı bulmuş oluruz?
1I AS1 0 1‘e ilişkin özvektör
2 I AS2 0 2‘e ilişkin özvektör
S1 c1V1
S2 c2V2
1t
xh (t ) e V1
c1
c1
e V2 M (t )
c2
c2
2t
M (t )
Özel çözüm:
x1ö zel (t )
xözel (t )
x
(
t
)
2ö zel
Tam çözüm:
Temel Matris
Nasıl belirleyeceğiz?
x(t ) M (t )C xözel (t )
C M (t0 )1x(t0 ) xözel (t0 )
x(t ) M (t )M 1(t0 )x(t0 ) xözel (t0 ) xözel (t )
x(t0 ) M (t0 )C xözel (t0 )
x(t ) M (t )M 1(t0 )x(t0 ) xözel (t0 ) xözel (t )
(t )
Durum Geçiş
Matrisi
x(t ) (t ) x(t0 ) xözel (t ) (t ) xözel (t0 )
x(t ) (t ) x(t0 ) xözel (t ) (t ) xözel (t0 )
öz çözüm
zorlanmış çözüm
t
x(t ) e At x(t0 ) e A(t ) Bu ( )d
öz çözüm
t0
zorlanmış çözüm
x1 3 0 x1 0
x
x u (t ),
2 2 2 2 1
x1 (0) 4 Durum denklemleri ile verilen
x (0)
2 5 sistem için tam çözümü bulunuz.
Bir özel hal:
x (t ) Ax(t )
Çözümü bir daha yazarsak
Otonom sistem
özvektörler
x(t ) e1 (t to ) S1x1 (t0 ) e2 (t to ) S2 x2 (t0 ) .....en (t to ) Sn xn (t0 )
özdeğerler
Çözüm, özvektörler ve özdeğerler ile nasıl değişir
.............................................................................................................
Özvektörleri aynı özdeğerleri farklı iki sistem
0
A1
1
5
2
11 1 2i
12 1 2i
2 5
A2
1
4
21 3 2i
22 3 2i
0.9129
0.9129
S11
S 21
0.1826 0.3651i
0.1826 0.3651i
S12
0.9129
0.9129
S 22
0
.
1826
0
.
3651
i
0.1826 0.3651i
Hangisi daha hızlı sıfıra yaklaşıyor ?
A1
sistemi
A2
sistemi
Özdeğerleri aynı özvektörleri farklı iki sistem
0.2 5
B1
1
0
.
3
11 0.25 2.235i
12 0.25 2.235i
0.2 1
B2
5
0
.
3
21 0.25 2.235i
22 0.25 2.235i
0.9125
S11
0
.
0051
0
.
4081
i
0.0051 0.4081i
S 21
0
.
9125
0.9125
0
.
0051
0
.
4081
i
0.0051 0.4081i
0
.
9125
S12
S 22
B1
sistemi
B2
sistemi
Bu durumda lineer sistemin çözümleri neler olabilir?
Tüm bu durum portrelerinde ortak bir şey var, ne?
S. Haykin, “Neural Networks- A Comprehensive
Foundation”2nd Edition, Prentice Hall, 1999,
New Jersey.
Dinamik sistemin özel bir çözümü: Denge noktası
Tanım: (Denge noktası) x f (x) sisteminin x(t ) xd , t t0 sabit
çözümleri, sistemin denge noktalarıdır.
xd nasıl belirlenir? 0 f ( x ) Cebrik denkleminin çözümleri denge noktalarıdır.
d
xd lineer sistemde
A matrisi tersinir ise tek aksi taktirde sonsuz
0
Ax
d
nasıl belirlenir?
tane
Hatırlatma
(Norm) V vektör uzayı olmak üzere aşağıdaki üç özelliği
sağlayan bağıntı “norm”’dur
. :V R
x 0 x0
x x
x y x y , x, y V
Bazı normlar Euclid Normu
Taksi Şöförü Normu
Hamming Mesafesi
Kararlılık
Sıfır giriş kararlılığı x (t ) Ax(t ), x(t0 ) x0
Tanım: (Lyapunov anlamında kararlılık)
x (t ) f ( x(t ))
herhangi bir 0
sistemine ilişkin bir denge noktası xd olsun. Verilen
için
x(t0 ) xd ( , t0 )
eşitsizliği
x(t ) xd , t t0
eşitsizliğini gerektirecek şekilde bir ( , t0 ) bulunabiliyorsa xd denge
noktası Lyapunov anlamında kararlıdır.
Tanım: (Asimptotik kararlılık)
x (t ) f ( x(t ))
sistemine ilişkin bir denge noktası xd olsun.
1) Sistem Lyapunov anlamında kararlı,
2)
x(t0 ) xd ( , t0 ) eşitsizliği
lim x(t ) xd 0, t t0 ifadesini gerektirecek
t
şekilde bir ( , t0 ) bulunabiliyorsa xd denge
noktası Asimptotik kararlıdır.
Teorem:
x (t ) Ax(t ), x(t0 ) x0 Sistemi Lyapunov anlamında kararlıdır
Nasıl oluyorda sistemin Lyapunov anlamında
kararlılığından bahsedebiliyoruz?
(t , t0 ) c, t t0