(Microsoft PowerPoint - ek soru-cevap

Örnek 29
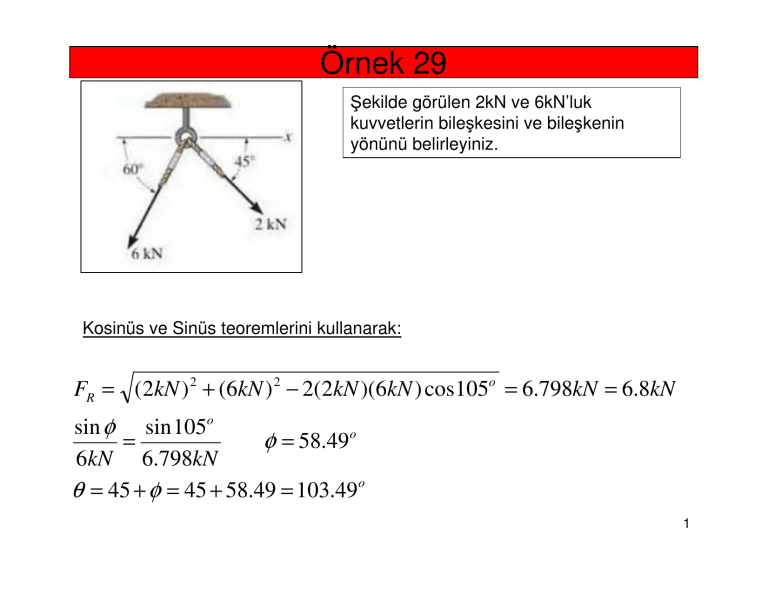
ekilde görülen 2kN ve 6kN’luk
kuvvetlerin bileşkesini ve bileşkenin
yönünü belirleyiniz.
Kosinüs ve Sinüs teoremlerini kullanarak:
FR = ( 2kN ) 2 + (6kN ) 2 − 2(2kN )(6kN ) cos105o = 6.798kN = 6.8kN
sin φ sin 105o
φ = 58.49o
=
6kN 6.798kN
θ = 45 + φ = 45 + 58.49 = 103.49o
1
Örnek 30
Çubuğun O noktasına etkiyen üç
kuvvetin bileşkesinin şiddetini ve
yönünü bulunuz.
2
3
4
Örnek 31
600 N
Bileşke kuvvetin şiddetini ve
yönünü bulunuz.
400 N
700 N
5
Örnek 32
Halkaya etkiyen bileşke
kuvvetin büyüklüğünü ve
doğrultu kosinüslerini bulunuz.
6
7
8
Örnek 33
F1 ve F2 kuvvetlerinin bileşkesinin
şiddeti 800 N ve yönü de z ekseni
doğrultusunda olduğuna göre, F2
vektörünün şiddetini ve doğrultu
kosinüslerini bulunuz.
9
10
Örnek 34
500 N
800 N
Kancanın ucuna etkiyen bileşke
kuvveti bulunuz.
4
3
(500 N ) ˆj + (500 N ) kˆ
5
5
= {400 ˆj + 300kˆ}N
F1 =
F2 = [(800 N ) cos 45] cos 30iˆ + [(800 N ) cos 45] sin 30 ˆj
+ (800 N ) sin 45(− kˆ)
= {489.90iˆ + 282.84 ˆj − 565.69kˆ}N
FR = F1 + F2 = {490iˆ + 683 ˆj − 266kˆ}N
11
Örnek 35
ekildeki A ve B noktalarına elastik bir bant
tutturulmuştur. Bantın uzunluğunu ve A’dan B’ye
ölçülen doğrultusunu belirleyiniz.
A’dan B’ye giden bir konum vektörü oluşturalım:
A(1m, 0, -3m)
B(-2m, 2m, 3m)
12
r doğrultusundaki birim vektörü yazalım:
Birim vektörün bileşenleri, doğrultu kosinüslerini verir:
Bu açılar, şekilde gösterildiği gibi,
r’nin başlangıcındaki A
noktasından başlayan bir koordinat
sisteminin pozitif eksenlerinden
ölçülmektedir.
13
Örnek 36
ekilde gösterilen adam ipi 70 lb’lik
bir kuvvetle çekmektedir. A
mesnedine etkiyen bu kuvveti
kartezyen vektör şeklinde ifade ediniz
ve doğrultusunu belirleyiniz.
A (0, 0, 30 ft)
B (6 ft, -8ft, 6ft)
A’nın x, y, z koordinatlarını
B’ninkilerden çıkartarak konum
vektörünü oluşturalım:
14
r ve F’nin doğrultusunu ve yönünü tanımlayan birim vektör
Kuvvet vektörü:
15
Örnek 37
ekildeki boruya B
ucundan, F=80 lb’lik
kuvvet uygulanmaktadır.
F ile BA parçası
arasındaki θ açısını ve
F’nin, BA’ya paralel ve
dik bileşenlerinin
büyüklüklerini belirleyiniz.
16
17
θ hesaplandığı için, aynı sonuç trigonometriden:
FBA = 80 cos 42.5 = 59 lb
F⊥ = F sin θ = 80 sin 45 = 54 lb
veya
F⊥ = F 2 − F 2 BA = (80) 2 − (59) 2 = 54 lb
18
Örnek 38
AB, BC ve CD kablolarında oluşan
kuvvetleri ve θ açısını bulunuz.
(B lambası 10 kg, C lambası 15 kg)
B noktasında;
∑ Fy = 0 ; TAB sin 15 − 10(9.81) N = 0
TAB = 379.03N = 379 N
∑ Fx = 0 ; TBC − 379.03 N cos15 = 0
TBC = 366.11N = 366 N
C noktasında;
∑ Fx = 0 ; TCD cos θ − 366.11N = 0
∑ Fy = 0 ; TCD − 15(9.81) = 0
TBC = 395 N
θ = 21.9o
19
Örnek 39
90 lb’lik yük şekildeki kancada asılıdır.
Yük iki ip ve k=500lb/ft katsayılı yay ile
tutulmaktadır. Denge durumunda,
iplerdeki kuvveti ve yayın gerilme
miktarını belirleyiniz. (AD ipi x-y
düzleminde, AC ipi x-z düzlemindedir.)
20
Önce serbest cisim diyagramını
çizelim:
21
Örnek 40
ekilde görülen 100kg’lık kutu, birine
yay bağlanmış üç iple tutulmaktadır.
Her bir ipteki çekme kuvvetini ve
yayın gerilme miktarını belirleyiniz.
Serbest cisim diyagramı:
22
F=ks
693.7=1500s
s=0.462m
23
Örnek 41
F kuvveti tarafından O noktası etrafında
oluşturulan momenti kartezyen vektör
olarak ifade ediniz.
24
1.yol
25
2.yol
26
Örnek 42
F kuvveti şekildeki desteğin
köşesinde etki etmektedir. Kuvvetin
O noktasına göre momentini
belirleyiniz (skaler ve vektörel
çözüm ile).
Çözüm 1- skaler analiz
27
Çözüm 2- vektörel analiz
28
Örnek 43
ekilde gösterilen çubuk, A ve B’deki
iki kelepçe tarafından tutulmaktadır.
F kuvvetinin ürettiği, çubuğu AB
ekseni etrafında döndürmeye çalışan
MAB momentini belirleyiniz.
29
30
Örnek 44
ekilde gösterilen desteğe
etkiyen kuvvetleri O noktasında
etkiyen bir eşdeğer bileşke
kuvvet ve kuvvet çifti momenti ile
değiştiriniz.
31
Kuvvet Toplamı
32
Moment Toplamı
33