ÖZEL TANIMLI FONKSİYONLAR − 6
( TERS FONKSİYONLAR )
FONKSİYONLAR BÖLÜM 6
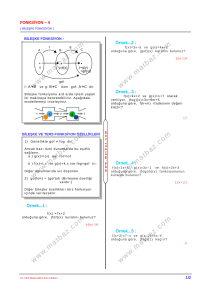
Örnek...2 :
R e e l s a yı l a r d a n r e e l s a yı l a r a t a n ım l ı
–1
f (x ) = 3 x + 1 f o nk s i yo n u i ç i n f ( 8 ) d e ğ e r i n i
h e s a p l a yı n ı z?
TERS FONKSİYON:
f , A k üm e s i n d e n B k üm e s i n e t a n ım l a n m ış
–1
b i r f o nk s i yo n o l s u n . B d e n A ya t a n ım l ı f
b a ğ ı n t ı s ı n ı n d a b i r f on k s i yo n o l m a s ı i ç i n f
f on k s i yo n u b i r e− b i r v e ö r t e n o lm a l ı d ı r.
–1
E ğ e r f b u ö ze l l i k l e r e s a h i p s e f e f i n
t e r s f o nk s i yo n u d e n i r.
Ş e k l i i n c e l e yi n i z.
f
A
B
Örnek...3 :
f
−1
U yg u n k o ş u l l a r d a f ( x ) = 2 x+ 3 i s e f −1 (7 )
d e ğ e r i n i h e s a p l a yın ı z .
y=f(x)
(y)=x
•
•
f(x)=y
⇔
f−1(y)=x
UYARI
–1
y= f ( x ) v e y= f ( x ) f o nk s i yo n l a r ı n ı n g r a f ik l e r i y= x ( 1 . A ç ı o r t a ya ) g ö r e s im e t r ik t i r.
y
y=f(x)
y=x
www.matbaz.com
f−1
Örnek...4 :
f (x ) = x 3 + x i s e f −1 (30 ) d e ğ e r i n i h e s a p l a yın ı z .
y=f −1(x)
x
0
Örnek...5 :
(
)
a b c
c a b
p e r m ü t a s yo n f o nk s i yo n u i ç i n f −1 (x) n e d i r ?
A = { a , b , c } k üm e s i n d e t a n ım l ı f =
Örnek...1 :
A={a,b,c} f:A → A ,f={(a,b),(b,b),(c,c)}
–1
–1
f o nk s i yo n u i ç i n f b a ğ ı n t ı s ı n ı ya z ı n ı z. f b i r
f o nk s i yo n m ud u r ?
12. Sınıf Matematik Konu Anlatımı 2014−2015
1/6
ÖZEL TANIMLI FONKSİYONLAR − 6
( TERS FONKSİYONLAR )
UYARI
UYARI
Ve r i l e n b i r f f o nk s i yo n u n u n k ur a l ı n ı
b u l m ak i ç i n a ş a ğ ı d ak i i k i a d ım i zl e n i r :
−d
a
ax+b
, f o nk s i yo }→ℝ−{ }, , f (x)=
c
c
cx+d
−dx +b
n u n t e r s i n i n k ur a l ı f −1 (x)=
d i r.
cx−a
f : ℝ−{
A d ım 1 ) Ve r i l e n f o nk s i yo n d a x i n y
c i n s i n d e d e ğ e r i b u l u n u r.
Örnek...10 :
A d ım 2 ) x v e y ye r d e ğ i ş t i r i l i r.
2x−3
, f o nk s i yo n u b i r e
3x−5
b i r v e ö r t e n s e a . b d e ğ e r i n i b u l u n u z?
f : ℝ−{a }→ ℝ−{b}, , f (x)=
Örnek...6 :
y= f ( x ) = 3 x + 5 f o nk s i yo n u n u n t e r s f o nk s i yo n u n u n k ur a l ı n ı b u l u n u z.
Örnek...7 :
Örnek...8 :
y= f ( x ) f o nk s i yo n u i ç i n
3y−2
eşitliği varsa
x=
y −4
www.matbaz.com
y= f ( x ) = a x + b f o nk s i yo n u n u n t e r s f o nk s i yo n u n u n k ur a l ı n ı b u l u n u z.
Örnek...11 :
ax+4
f : ℝ−{1}→ℝ−{2} , f (x )=
, f on k s i yo n u b i r e
cx+5
b i r v e ö r t e n s e a . c d e ğ e r i n i b u l u n u z?
f −1 (x) i b u l u n u z .
Örnek...12 :
f : R + → R + y= f ( x ) = x ² f o n k s i yo n u n t e r s
f on k s i yo n u n k u r a l ı n ı b u l u n u z.
Örnek...9 :
f : ℝ−{−3}→ℝ−{2}, f (x )=2x−1 , f on k s i yo n u n
x+3
t e r s f o n k s i yo n u n k ur a l ı n ı b u l u n u z .
12. Sınıf Matematik Konu Anlatımı 2014−2015
2/6
ÖZEL TANIMLI FONKSİYONLAR − 6
( TERS FONKSİYONLAR )
Örnek...13 :
Örnek...16 :
U yg u n ş a r t l a r a l t ın d a f (x)=3.4 x −1
f on k s i yo n u n u n t e r s i n i n k ur a l ın ı b u l u n u z?
f : [ − 2 , ∞ ) , → [ − 4 , ∞ ) , y= f ( x ) = x ² + 4 x
f o nk s i yo n u n t e r s f o nk s i yo n u n k u r a l ı n ı
bulunuz?
Örnek...17 :
Örnek...14 :
U yg u n ş a r t l a r a l t ın d a f (x)=e x +3 +5
f on k s i yo n u n u n t e r s i n i n k ur a l ın ı b u l u n u z?
3
www.matbaz.com
R e e l s a yı l a r d a
f (x)= √ 7x+2−4
f o nk s i yo n u n u n t e r s i n i n k u r a l ı n ı b u l u n u z ?
Örnek...15 :
1
,∞ ) , → K⊂ℝ f (x)=log 3(2x−1)
2
f o nk s i yo n u n u n t e r s i n i n k u r a l ı n ı b u l u n u z ?
f:(
Örnek...18 :
y
Grafiği verilen
y= f ( x ) f o n k i yo nu için
5
f −1(4)+f−1 (0)
=?
f−1(5)
4
y=f(x)
x
−2
12. Sınıf Matematik Konu Anlatımı 2014−2015
0
8
3/6
ÖZEL TANIMLI FONKSİYONLAR − 6
( TERS FONKSİYONLAR )
Örnek...19 :
y
y=f(x+3)
6
y= f ( x + 3 ) ü n g r a f i ğ i n e
f −1(0)
göre,
değeri
f −1(3)
kaçtır?
4
x
2
−3
0
1
Örnek...20 :
y
y=f(x+1)
G r af i ğ i v e r i l e n
y= f ( x + 1 ) f on k i yo n u
f −1 (2)
için
=?
f −1 (3)
3
2
x
−1
0
12. Sınıf Matematik Konu Anlatımı 2014−2015
1
www.matbaz.com
−3
4/6
ÖZEL TANIMLI FONKSİYONLAR − 6
( TERS FONKSİYONLAR )
DEĞERLENDİRME
1)
(
A={1,2,3} kümesinde tanımlı f = 1 2 3
2 3 1
permütasyon fonksiyonu için f
yazınız.
−1
5)
)
y=f(x+3) ün grafiğine
göre,
fonksiyonunu
y
y=f(x+3)
6
−1
f (4 )
+m. f−1 (0)=0
f (−3)
4
−1
ise m değeri kaçtır?
2
−3
x
0 1
−3
2)
√ 2−kx fonksiyonu
f : ℝ−{c}→ℝ−{−4} , f (x )=
3x +5
bire bir ve örtense k.c değerini bulunuz?
3) f: (−∞, 1 ) , f(x)=x2−10x−6 fonkiyonunun tersinin
2
kuralını bulunuz?
4) f(x)=x3+3 fonkiyonunun tersinin kuralını
bulunuz?
12. Sınıf Matematik Konu Anlatımı 2014−2015
www.matbaz.com
6) f doğrusal bir fonksiyon ve f(2)=3 , f−1(2)=5 ise
f(0) =?
7) 2x.f(x)−3=f(x)−x eşitliğiyle uygun şartlarda
verilen y=f(x) fonksiyonun tersinin kuralını
bulunuz?
5/6
ÖZEL TANIMLI FONKSİYONLAR − 6
( TERS FONKSİYONLAR )
8) y=f(x) fonksiyonu için x.y −4=1+3y eşitliği
11) Uygun koşullarda tanımlı f (x )=73x +2 −5
fonkiyonunun tersinin kuralını bulunuz?
5
varsa f-1(x)=?
−3
, ∞)→K⊂ℝ , f (x )=7−log 2 (3 +5x )
5
fonkiyonunun tersinin kuralını bulunuz?
f:(
www.matbaz.com
9)
10) Uygun koşullarda tanımlı f (x )=3+ln(ex−2)
fonkiyonunun tersinin kuralını bulunuz?
12. Sınıf Matematik Konu Anlatımı 2014−2015
6/6