elektrik devre temelleri

ELEKTRİK DEVRE TEMELLERİ
Öğretim üyesi: Doç. Dr. S. Özoğuz
Tel: 285 36 19
Ders saati:
e-posta: serdar@ehb.itu.edu.tr
Pazartesi, 10.00-13.00 / D-4102
İçindekiler
1. Devre teorisi, toplu parametreli devreler, Kirchhoff’un gerilim ve akım yasaları
2. Graf teorisi; temel tanımlar, lineer bağımsız denklem takımları
3. Bazı 2- ve 3- uçlu devre elemanlari, paralel-seri bağlantı
4. Genel direnç devreleri, Norton ve Thevenin eşdeğer devreleri, lineer olmayan
devreler
5. Dinamik devrelere giriş ve durum denklemleri
6. RLC ve çok uçlulardan oluşmuş devrelerde durum denklemlerinin elde edilmesi
7. İkinci mertebeden devreler
Kaynaklar:
1- Linear and Nonlinear Circuits L.O.Chua, C.A.Desoer, E.S.Kuh 1987-Mc Graw
Hill
2- Devre Analizi Dersleri Kisim I Prof. Dr. Yilmaz Tokat 1986-Çaglayan Kitapevi
3- Elektrik Devrelerinin Analizi Prof. Dr. Cevdet Acar 1995-I.T.U Elektrik-Elektronik
Fak.
4- Electric Circuits J.W.Nilsson 1994-Adison-Wesley-literature
5- Analysis of Linear Circuits Clayton R.Poul- Mc Graw Hill
6- M. H. Rashid, ”SPICE for Circuits and Electronics Using PSpice”, Prentice-Hall,
1995, New Jersey.
ELEKTRİK DEVRE TEMELLERİ
Amaç: Fiziksel devrelerin elektriksel davranışlarını niceliksel ve
niteliksel olarak öngörme
akım [A], gerilim [V]
Fiziksel devrede elemanların uçlarındaki akım ve gerilim, ölçme
elemanlarının koordinatlarına bağlı değil ise devreye toplu
parametreli devre denir. Aksi halde devre dağılmış parametreli
devre olarak adlandırılır.
Toplu parametreli devrede devrenin fiziksel uzunluğu d, işaretin
dalga boyundan çok küçük olmalıdır.
d << c/f
d=1mm⇒t=10-3/3.108=0,0033 ns
Uygulama alanı:
Gerilim µV (10-6)
Akım
fA (10-15)
Frekans 0 Hz
Güç
MV (106 V)
10-14W
MA
1GHz (109Hz)
1GW
Tanımlanmamış büyüklükler:
Akım i(t) [A] ve gerilim v(t) [V] devre teorisinin tanımlanmamış
büyüklükleridir.
Fiziksel devre ve model
İşaret üreteci, transformatör, pil, transiztör, direnç gibi elektrik
devrelerini oluşturmakta kullanılan aletlerden oluşmuş fiziksel
devreye karşı düşen, tanım bağıntıları ile tanımlı ideal devre
elemanlarından oluşan model oluşturulur. Devrenin çalışma
koşullarına (uygulanan kaynak büyüklükleri, incelemenin yapıldığı
frekans aralığı gibi) bağlı olarak aynı fiziksel devreye birden fazla
elektriksel model karşı düşebilir. Her model bir yaklaşıklıktır.
Fiziksel model ⇒ Fiziksel elemanlar
Devre modeli ⇒ Devre elemanları (eleman modeli)
Elemanların akım, gerilim yönleri
i1=2mA,
i2= -3mA, v1=3mV=vd1=vd2+3mV
1
A
Uyarma
Devresi
i(t)
+
v(t)
V
–
2
Kirchhoff'un gerilim yasası
n düğümlü birleşik ve toplu parametreli bir devrede herhangi bir
düğümü şekildeki gibi referans seçerek, (n-1) düğüm gerilimi
tanımlayalım.
Kirchhoff'un gerilim yasası (KGY)
vk-j=ek-ej
Kapalı düğüm dizileri için KGY
Tüm kapalı düğüm dizileri için, düğümler arası geriimlerin toplamı
sıfırdır.
Örnek:
1 - 2- 3-1
v12+v23+v31=0
KGY ⇔ kapalı düğüm dizileri için KGY
⇒1 - 2- 3-1
v12+v23+v31=(e1-e2)+(e2-e3)+(e3-e1)=0
⇐ v12+v23+v31=0 olsun.
3 düğümü referans ise
v23=e2, v31=-e1, v12+e2-e1=0
v12=e1-e2
Örnek:
vA=v12=e1-e2, vC=v23=e2-e3
2 - 4- 5- 2
T:
v24+v45+v52=0
v25=e2-e5=e2, v45=e4
1- 2- 3-4- 5 -1
v42=e4-e2
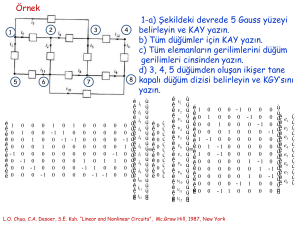
Gauss-yüzeyi: Sadece devre elemanlarını birleştiren bağlantıları
kesecek şekilde çizilmiş çift yönlü kapalı yüzey
Kirchhoff'un akım yasası (KAY)
Toplu parametreli devrelerde, tüm Gauss yüzeyleri için, her t
anında, Gauss yüzeyini kesen akımların cebirsel toplamı sıfırdır.
Düğümler için KAY: Bir düğümden çıkan akımların toplamı
sıfırdır.
i1 + i2 - i3 = 0
i1
i3
i2
Örnek:
S1: i1+i4+i5+i6=0
S4: -i4-i10-i7=0
S5: -i12-i3-i11-i8-i9=0
KAY ve KGY
- Toplu parametreli devrelerde
- Eleman özelliklerinden bağımsız
- Elde edilen denklemler katsayıları +1, -1 veya 0 olan lineer
denklemler
Graf teorisi
dal ve düğümlerden oluşan topolojik yapı
4
5
a
1
7
b
c
6
düğüm sayısı=4
dal sayısı=7
3
2
d
Uç graf
i
1
1
+
i
v
–
2
uygun yön
p=v.i
2
i1
c
+
3-uçlu
v1
i2
v2
–
–
e
+
d
d
c
v2, i2
v1, i1
e
n-uçlu elemana ilişkin uç grafı
2-kapılılar ve çok-kapılılar
1 i1
i2 2
+v
2
–
2'
v1+
–
1'
2
1
1
1'
2
2'
1
i1
v1+
–
i2
3-kapılı
v2+
–
i3
+
v3
–
1
3
1'
3
2
2
2'
2-kapılıların uç grafları ayrık
Ancak her ayrık graf aşağıdaki şekilde gösterildiği gibi, birleşik bir
grafa dönüştürülebilir.
Aşağıdaki altdevre hem 2-kapılı, hem de 3-uçlu olarak düşünülebilinir.
3'
Verilen bir devrede, her elemana ilişkin uç grafı çizilerek elde
edilen topolojik yapıya devre grafı denir.
Analiz = matematiksel model(ne)+bağlantı denklemleri (ne)
Bağlantı denklemleri: Akım denklemleri+gerilim denklemleri
(Bağlantı denklemleri elemanın cinsine bağlı değil)
Devre grafı: Devre elemanlarının özelliklerine bakılmaksızın
düğümler
arasındaki
bağlantının
mevcut
olup
olmadığını
belirleyen, yönlendirilmiş doğru parçalarından oluşmuş geometrik
yapı
Graf elemanı: İki düğüm arasındaki bağlantıyı gösteren
yönlendirilmiş doğru parçası
Düğüm: graf elemanının uçları. (küçük harfle gösterilir.)
İlmek: Tek düğümlü graf elemanı
Graf: Aralarında bazılarının ortak noktalarının olduğu sonlu
sayıda graf elemanının oluşturduğu yapı
Derece: bir düğüme bağlı graf elemanı sayısı
δ(di)=4
di
Ayrık düğüm: derecesi 0 olan düğüm
ne adet eleman ve n adet düğüm içeren bir grafta düğümlere ilişkin
derecelerin toplamı eleman sayısının iki katına eşittir.
Alt graf: Bir G grafının bazı elemanlarından oluşmuş yeni grafa
G'nin alt grafı denir.
Yol: G'nin, Gy alt grafı
a) Gy'nin n adet elemanı varsa, düğüm sayısı n+1 'dir
b) Gy'deki düğüm ve elemanlar d1, d2, .. ve e1,e2,.. olarak
numaralandırılırsa, herhangi bir ei elemanının ilişkin düğümler di
ve di+1 olur
c) birinci ve sonuncu düğümlerin dereceleri 1, diğerlerinin 2 dir.
Birleşik graf: Bir grafın herhangi iki düğümü arasında an az bir
yol varsa, bu grafa birleşik graf denir. Aksi halde, grafa ayrık graf
denir.
Parça: Ayrık bir G grafında aralarında en az bir yol bulunan
elemanlardan oluşmuş birleşik altgraflarının aralarında ortak ne bir
eleman, ne bir düğüm varsa, bu alt graflar G'nin parçalarıdır .
Çevre: Bir grafın tüm düğümlerinin derecesi 2 olan birleşik bir alt
grafına çevre denir.
Çevre yönü çizgisi: Çevrenin elemanlarını izleyecek biçimde
çevre içerisinde çizilmiş yönlü eğri.
Ağaç: Birleşik bir G grafının birleşik, G'nin tüm düğümlerini
içeren ve çevre içermeyen alt grafına ağaç denir.
Ağacın elemanlarına dal, ağaç dışı elemanlara da kiriş denir.
1. ne elemanlı ve nd düğümlü bir grafta dal elemanlarının sayısı
nd-1, kiriş elemanlarının sayısı ne-nd+1 dir.
2. Bir ağaç alt kümesinde düğümler arasında bir ve yalnız bir yol
vardır.
3. Seçilen bir ağaçtan sonra geriye kalan kiriş elemanlarının
oluşturduğu kümeye ağaç tümleyeni ya da kirişler kümesi denir.
Temel çevreler kümesi:
ne elemanlı ve nd düğümlü birleşik bir grafta GT ağacını seçelim.
GT grafının ne-nd+1 kirişinden her biri, sadece GT grafına ait olan
elemanlar (dallar) ile bir çevre oluşturur.
Bu şekilde elde edilen ne-nd+1 çevreye temel çevreler kümesi
denir.

1
13
{
2
€
5
3
|
8
7
}
9
10
4
6
~
11
12

Temel çevreler kümesi:
{8, 7}
{9, 7, 6}
{3, 12, 2}
{13, 1, 2}
{11,10, 12}
toplam ne-nd+1=13-7+1=7
Kesitleme: G'nin içindeki bazı elemanlar aşağıdaki özellikleri
sağlıyorsa, bunlara kesitleme kümesi denir.
a) Bu elemanlar graftan çıkarılırsa, graf iki parçaya ayrılır,
b) Bu kümenin hiç bir alt kümesi a) yı sağlamaz.
kesitleme çizgisi
2
B
A
d1
1
A
6
d2
5
kesitleme yönü
7
8
4
d3
d5
3
d4 B
B
Düğümlerin bir kısmına A,
diğerlerine
B
denilsin
(düğüm ayrımlaması).
İki ucu farklı harfli olan
elemanlar
bir
kesitleme
oluşturur.
Dikkat: Her düğüm ayrımlamasından bir kesitleme elde edilmez.
d3=A, d2=B
Temel Kesitlemeler Kümesi:
ne elemanlı ve nd düğümlü birleşik bir grafta GT ağacını seçelim.
GT grafının nd-1 dalından her biri, sadece GT' grafına ait olan
elemanlar (kirişler) ile bir kesitleme oluşturur.
Bu şekilde elde edilen nd-1 kesitlemeye temel kesitlemeler kümesi
denir.

1
{
2
€
5
ne=13 => dal nd-1=7-1=6
3
|
8
Birleşik graf
13
7
}
10
4
6
~
9
nd=7=> kiriş ne-nd+1=7
12

11
• Kirişler kümesi
GK={3, 4, 5, 8, 9, 11, 13}
• Dallar kümesi

GT={1, 2, 6, 7, 10, 12}
1
13
{
2
5
|
8
6
7
}
9
3
4
~
11
€
10
{5, 4, 10, 11} bir kesitlemedir
12

• Düğüm kesitlemesi GDK={1, 2, 3, 4 , 5}
1. numaralı düğüm ayrık parça
Bir G birleşik grafının G1 ve G2 altgrafları aşağıdaki koşulları
sağlıyor ise:
1. G1 ve G2 nin ortak elemanları yok
2. G1 içinde çevre yok (ağaç)
3. G2, G'in herhangi bir kesitlemesine sahip değil (kirişler),
G de bir GT ağacı seçilebilir.
Graf Matrisleri
1. Temel çevreler matrisi
G (birleşik) grafındaki temel çevreler kümesine ait Bt=[bij] matrisi
bij=0;
(devrenin) j. elemanı i. temel çevrede bulunmuyorsa,
bij=1;
j. elemanı i. temel çevrede bulunuyor ve bu elemanın
yönü çevre yönü ile aynı ise,
bij=-1;
j. elemanı i. temel çevrede bulunuyor ve bu elemanın
yönü çevre yönüne ters ise,
alınırsa, Bt’ye temel çevreler matrisi denir. (çevre yönü=kiriş yönü)
8
6 B nin boyutu (n -n +1) x (n )
t
e d
e
1
3
2
4
10
Bt =
5
9
7
1
2
3
4
5
6
7
8
9
10
(8)
-1
0
-1
0
-1
1
0
1
0
0
(9)
0
0
0
-1
1
0
-1
0
1
0
(10)
0
1
-1
-1
0
0
0
0
0
1
1444442444443 14243
dallar
kirişler
Bt = [
B1
M
U
]
123
123
nd-1
ne-nd+1
ne-nd+1
6
1
7
Bt
4
1
5
2
(7)
= (8)
(9)
3
4
5
9
Bt = [
B1
M
U
]
Rank {Bt} = ne-nd+1= kiriş sayısı = temel çevre sayısı
2. Temel kesitlemeler matrisi
G grafındaki temel kesitlemeler kümesine ait Qt=[qij] matrisi
qij=0;
(devrenin) j. elemanı i. temel kesitlemede
bulunmuyorsa,
qij=1;
j. elemanı i. temel kesitlemede bulunuyor ve bu
elemanın yönü kesitleme yönü ile aynı ise,
qij=-1;
j. elemanı i. temel kesitlemede bulunuyor ve bu
elemanın yönü kesitleme yönüne ters ise,
alınırsa, Qt’ye temel kesitlemeler matrisi denir.
(kesitleme yönü = dal yönü)
6
7
8
9
0 0 0 -1 -1 1 1 0 0
1 1 0 -1 0 0 0 1 0
0 -1 -1 0 -1 0 0 0 1
144424443 14243
dallar
kirişler
3
8
2
4
5
7
1
1
6
3
Qt
2
Qt = [
(4)
= (5)
(6)
(7)
2
3
1 1 -1
-1 -1 1
0 1 -1
-1 -1 0
14243
B1
4
3
1 0 0
0 1 0
0 0 1
14243
dallar
U
M
Q1 ]
123
123
nd-1
ne-nd+1
1
Bt
(1)
= (2)
(3)
2
5
6
7
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1
142443
U
B1= -Q1T
QtBtT=0 ⇔ BtQtT=0
⎡B1T ⎤
QtBt = [U Q1][B1 U] = [U Q1 ] ⎢ ⎥
⎣U⎦
T
T
= B1T+Q1 = B1T+( -B1T) = 0
5
6
7
-1 1 0 1
-1 1 -1 1
1 -1 1 0
1442443
kirişler
nd-1
Q1= -B1T
Özellik:
4
3. Düğümler matrisi
G grafındaki parçalarından biri tek bir düğüm olan kesitlemeler
kümesi ele alınsın ve kesit yönü tek düğüm olan parçadan diğerine
doğru olsun. Bu kümeye ait A=[aij] matrisi
aij=0;
(devrenin) j. elemanı i. düğüm kesitlemesinde
bulunmuyorsa,
aij=1;
j. elemanı i. düğüm kesitlemesinde ve yönü düğümden
uzaklaşan yönde ise,
aij=-1;
j. elemanı i. düğüm kesitlemesinde ve yönü düğümden
yaklaşan yönde ise,
alınırsa, A’ya düğümler matrisi denir.
9 A nın boyutu ( nd ) x ( ne )
4
5
a
7
1
b
c
6
2
d
3
A
(a)
= (b)
(c)
(d)
1
2
3
4
5
6
7
1
0
-1
0
0
0
1
-1
0
1
0
-1
-1
1
0
0
1 0
-1 1
0 -1
0 0
1
0
0
-1
4. İndirgenmiş düğümler matrisi, A
A matrisinden bir satır silinerek elde edilen matris
A
(a)
= (b)
(c)
(d)
1
2
3
4
5
6
7
1
0
-1
0
0
0
1
-1
0
1
0
-1
-1
1
0
0
1 0
-1 1
0 -1
0 0
1
0
0
-1
rank A = nd-1
* nd düğümlü birleşik bir grafına ilişkin indirgenmiş düğümler
matrisi, A’nın nd-1 satır ve nd-1 sütunlu altmatrislerinin tekil
olmamaları için gerek ve yeter koşul, bu altmatrislerin sütunlarına
ilişkin elemanların G’nin içindeki bir ağacın dalları olmalarıdır.
A’nın özellikleri:
A1
M
A2 ]
nd-1 ⇒
123
123
dallar
kirişler
-1
-1
A1 A = [ U M A1 A2 ] = QT = [ U M Q1 ]
9
A=[
⇒
Q1 = A1-1A2
A1-1A=QT
4
5
1
1
7
6
(a)
= (b)
(c)
A
3
2
A=[
A1
A2
M
⎡ 1 0 0⎤
A 1 = ⎢ 0 0 1⎥
⎢
⎥
⎢⎣− 1 1 0 ⎥⎦
2
3
1 0 0
0 0 1
-1 1 0
14243
dallar (A1)
4
]
⎡- 1 1 0 1⎤
A2 = ⎢ 1 - 1 1 0 ⎥
⎢
⎥
⎢⎣ 0 0 - 1 0 ⎥⎦
Qt
(1)
= (2)
(3)
2
3
1 0 0
0 1 0
0 0 1
14243
dallar (U)
4
5
6
7
-1 1 0 1
-1 1 -1 1
1 -1 1 0
1442443
kirişler (Q1)
6
7
-1 1 0 1
1 -1 1 0
0 0 -1 0
1442443
kirişler (A2)
⎡1 0 0⎤ ⎡ 1 0 0 − 1 1 0 1⎤
Q t = A1−1 A = ⎢1 0 1⎥ ⎢ 0 0 1 1 − 1 1 0⎥
⎢
⎥⎢
⎥
⎢⎣0 1 0⎥⎦ ⎢⎣− 1 1 0 0 0 − 1 0⎥⎦
1
5
Devreler Teorisinin 2. Postülası
G grafında seçilmiş bir ağaca ilişkin temel çevreler matrisi Bt
G nin elemanlarının gerilimlerinin oluşturduğu vektör, v(t)
Bt v(t) = 0
Bu bağıntıya temel çevre denklemleri adı verilir.
5
7
2
1
nd=5, ne=8
4
3
6
Bt v(t)=0
8
Bt =
1
2
3
4
5
6
7
8
(5)
-1
-1
0
0
1
0
0
0
(6)
0
1
0
-1
0
1
0
0
(7)
-1
0
1
0
0
0
1
0
(8)
0
0
-1
-1
0
0
0
1
1442443 1442443
dallar (B1)
kirişler (U)
temel çevre denklemleri
(5)
-v1(t)- v2(t)+ v5(t)
=
0
(6)
v2(t)- v4(t)+ v6(t)
=
0
(7)
- v1(t)+ v3(t)+ v7(t)
=
0
(8)
- v3(t)- v4(t)+ v8(t)
=
0
v1(t)
v2(t)
v3(t)
v4(t)
v(t) = v5(t)
v6(t)
v7(t)
v8(t)
Devreler Teorisinin 3. Postülası
G grafında seçilmiş bir ağaca ilişkin temel kesitlemeler matrisi Qt
G nin elemanlarının akımlarının oluşturduğu vektör, i(t)
Qt i(t) = 0
Bu bağıntıya temel kesitleme denklemleri adı verilir.
5
a
7
1
3e
c
b
2
4
nd=5, ne=8
6
Qt i(t)=0
d
8
Qt =
1
2
3
4
5
6
7
8
(1)
1
0
0
0
1
0
1
0
(2)
0
1
0
0
1
-1
0
0
(3)
0
0
1
0
0
0
-1
1
(4)
0
0
0
1
0
1
0
1
1442443 1442443
dallar (U)
kirişler (Q1)
temel kesitleme denklemleri
(1)
i1(t)+ i5(t)+ i7(t) =
0
(2)
i2(t)+ i5(t) - i6(t) =
0
(3)
i3(t) - i7(t)+i8(t) =
0
(4)
i4(t)+ i6(t)+ i8(t) =
0
i1(t)
i2(t)
i3(t)
i4(t)
i(t) = i5(t)
i6(t)
i7(t)
i8(t)
Qt=A1-1A olduğundan
⇔
Qt i(t) = 0
[
A1
A i(t) = 0
]
A2
14243 14243
dallar
kirişler
⎡ i1 (t) ⎤
⎢i (t)⎥ = 0
⎣2 ⎦
Her iki tarafı soldan A1-1 ile çarparsak
[
⎡ i (t) ⎤
A 2 ] ⎢ 1 ⎥ = U A1−1 A 2
⎣i 2 (t)⎦
A1−1 [A1
⎤
]⎡⎢ii (t)
= [U
(t)⎥
1
⎡ i (t) ⎤
Q1 ] ⎢ 1 ⎥ =
⎣i 2 (t)⎦
2
⎦
1
2
3
4
5
6
7
8
1
0
0
0
-1
0
-1
0
0
1
0
0
1
0
-1
0
0
0
-1
1
1
-1
0
0
0
0
1
0
-1
0
1
0
-1
0
0
0
0
1
-1
0
⎣
⎡ i (t) ⎤
Q t ⎢ 1 ⎥ = Q t i(t) = 0
⎣i 2 (t)⎦
5
a
7
c
b
2
1
3
e
8
4
6
d
A
a
= b
c
d
e
İndirgenmiş düğümler matrisi, A
1
A
a
= b
c
d
2
3
4
1 0 0 0
0 -1 0 0
0 0 1 0
0 0 0 -1
1442443
A1
5
6
7
i1(t)
i2(t)
i3(t)
i4(t)
i5(t)
i6(t)
i7(t)
i8(t)
8
i1(t)
1 0 1 0
-1 1 0 0
0 0 -1 1
0 -1 0 -1
142443
A2
i(t) =
=
İ2(t)
Düğüm denklemleri, A i(t) = 0
(a)
i1(t)+ i5(t)+ i7(t) =
0
(b)
- i2(t)- i5(t)+ i6(t)=
0
(c)
i3(t)- i7(t)+ i8(t) =
0
(d)
- i4(t)- i6(t)- i8(t) =
0
⎡1 0
⎢0 − 1
−1
A1 A 2 = ⎢
⎢0 0
⎢
⎣0 0
A1−1 [A1
0⎤
0⎥
⎥
0⎥
⎥
0 − 1⎦
0
0
1
[
⎡1 0
⎢
−1 ⎢0 − 1
A1 =
⎢0 0
⎢
⎣0 0
0⎤
0⎥
⎥
0⎥
⎥
0 − 1⎦
0
0
1
⎡ 1 0 1 0 ⎤ ⎡1 0 1
⎢− 1 1 0 0 ⎥ ⎢1 − 1 0
⎢
⎥=⎢
⎢ 0 0 − 1 1 ⎥ ⎢0 0 − 1
⎢
⎥ ⎢
⎣ 0 − 1 0 − 1⎦ ⎣0 1 0
⎡ i (t) ⎤
A 2 ] ⎢ 1 ⎥ = U A1−1 A 2
⎣i 2 (t)⎦
⎤
]⎡⎢ii (t)
= i (t) + Q i (t) = 0
(t)⎥
1
⎣
2
⎦
1
1 2
0⎤
0⎥
⎥ = Q1
1⎥
⎥
1⎦
Toplam ani güç özelliği ve Tellegen teoremi
İki farklı D ve D' devresi aynı G grafına sahip olsun.
D grafı
D' grafı
Bt v(t) = 0
Bt v'(t) = 0
Qt i(t) = 0
Qt i'(t) = 0
(v(t), i(t) ile v'(t), i'(t) farklı)
Daha açık olarak
[B1
⎡ v (t) ⎤
U] ⎢ 1 ⎥ = 0
⎣ v 2 (t)⎦
[B1
⎡ v' (t) ⎤
U] ⎢ 1 ⎥ = 0
⎣ v'2 (t)⎦
[U
⎡ i (t) ⎤
Q1 ] ⎢ 1 ⎥ = 0
⎣i 2 (t)⎦
[U
⎡ i' (t) ⎤
Q1 ] ⎢ 1 ⎥ = 0
⎣i'2 (t)⎦
v2(t) + B1 v1(t) = 0
v'2(t) + B1 v'1(t) = 0
i1(t) + Q1 i2(t) = 0
i'1(t) + Q1 i'2(t) = 0
v2(t) = -B1 v1(t)
v'2(t) = -B1 v'1(t)
i1(t) = -Q1 i2(t)
i'1(t) = -Q1 i'2(t)
[
]
⎡ i (t) ⎤
v T (t)i(t) = v1T (t) v T2 (t) ⎢ 1 ⎥ = v1T (t) i1 (t) + v T2 (t) i 2 (t) =
⎣i 2 (t)⎦
v1T(t) [ -Q1i2(t) ] + [ -v1T(t)B1T ] i2 (t)=
v1T(t) B1T i2(t) – v1T(t) B1T i2T(t) = 0 ( Q1 = -B1T )
yani vT(t)i(t) ≡ 0
Aynı şekilde Q1 ve B1 matrislerine sahip D' grafı için de
v'T(t) i'(t) ≡ 0
vT(t) i'(t) ≡ 0
v'T(t) i(t) ≡ 0
bağıntıları gösterilebilinir.
Buradan aşağıdaki teoremleri yazabiliriz.
Toplam ani güç özelliği
Bir devredeki toplam ani güç
T
ne
p (t ) = v(t) i(t) = ∑ v k (t)ik (t) ≡ 0
k =1
özdeş olarak sıfırdır. Yani üretilen enerji = tüketilen enerji
Telegen teoremi
Grafları aynı olan D ve D' graflarında çapraz ani güçlerin
toplamı özdeş olarak sıfırdır.
p1(t) = vT(t) i'(t) ≡ 0
p2(t) = v'T(t) i(t) ≡ 0
Devreler teorisindeki devrelerin özellikleri
1) Gerilim kaynaklları aralarında çevre oluşturmazlar
2) Akım kaynakları aralarında kesitleme oluşturmazlar.
Bu türden devrelere uygun devreler denir. Aksi halde, devre ancak
uygun kaynak fonksiyonları için kısmen çözülebilir.
Denklem kurma ağacı
Teorem: Uygun ve birleşik bir D devresinin grafı G ise, G'de öyle
bir ağaç seçilebilir ki, bu ağaç tüm gerilim kaynaklarına ilişkin graf
elemanlarını dal olarak içine alır ve tüm akım kaynaklarına ilişkin
graf elemanları bu ağacın dışında kalır.
Bu ağaca denklem kurma ağacı denir.
Denklem kurma ağacı seçilmiş grafa ilişkin denklemler
⎡ B11
⎢B
⎣ 21
B12
U
B 22
0
⎡U 0 Q11
⎢0 U Q
⎣
21
0⎤
U ⎥⎦
⎡ v e (t) ⎤
⎢ v (t)⎥
⎢ d ⎥=0
⎢ v k (t)⎥
⎥
⎢
⎣ v j (t) ⎦
⎡ i e (t) ⎤
⎢
⎥
Q12 ⎤ ⎢i d (t)⎥
= 0 şeklinde bölümlendirilebilir.
Q 22 ⎥⎦ ⎢i k (t)⎥
⎢
⎥
⎣ i j (t) ⎦
⎡ v k (t)⎤
⎡ B11
=
−
⎢ v (t) ⎥
⎢B
⎣ 21
⎣ j ⎦
⎡ i e (t) ⎤
⎡Q11 Q12 ⎤ ⎡i k (t)⎤
=
−
⎥
⎢i (t)⎥
⎢Q
⎥⎢
⎣ 21 Q 22 ⎦ ⎣ i j (t) ⎦
⎣d ⎦
B12 ⎤ ⎡ v e (t) ⎤
;
B 22 ⎥⎦ ⎢⎣ v d (t)⎥⎦
Tüm gerilimlere ilişkin v(t) vektörü
⎡ v e (t) ⎤ ⎡ U
⎢
⎥ ⎢
⎡ v1 (t) ⎤ ⎢ v d (t)⎥ ⎢ 0
v(t) = ⎢
⎥ = ⎢ v (t)⎥ = ⎢ − B
v
(t)
k
⎣ 2 ⎦
11
⎢
⎥ ⎢
⎣ v j (t) ⎦ ⎣− B 21
0 ⎤
U ⎥ ⎡ v e (t) ⎤
⎥
− B12 ⎥ ⎢⎣ v d (t)⎥⎦
⎥
− B 22 ⎦
Ayrıca
B11 = -Q11T, B12 = -Q21T, B21 = -Q12T, B22 = -Q22T
yardımıyla
⎡ U
⎢ 0
v(t) = ⎢ T
⎢Q11
⎢ T
⎣Q12
0 ⎤
U ⎥ ⎡ v e (t) ⎤ ⎡ U ⎤
⎥
v1 (t)
=
Q T21 ⎥ ⎢⎣ v d (t)⎥⎦ ⎢⎣Q1T ⎥⎦
⎥
Q T22 ⎦
olarak bulunur.
Benzer şekilde
⎡ i e (t) ⎤ ⎡ − Q11
⎥ ⎢
⎢
⎡ i1 (t) ⎤ ⎢ i d (t) ⎥ ⎢− Q 21
i(t) = ⎢
⎥ = ⎢i (t)⎥ = ⎢ U
i
(t)
k
⎣2 ⎦
⎥ ⎢
⎢
⎣ i j (t) ⎦ ⎣ 0
olmaktadır.
− Q12 ⎤
− Q 22 ⎥ ⎡i k (t)⎤ ⎡B1T ⎤
⎥⎢
⎥ = ⎢ ⎥ [i 2 (t)]
0 ⎥ ⎣ i j (t) ⎦ ⎣ U ⎦
⎥
U ⎦