![(Microsoft PowerPoint - B\326L\334M 5 [Uyumluluk Modu])](//s1.studylibtr.com/store/data/000988762_1-e33fda01f39f1f6a45a09c25b7c42bd4-768x994.png)
18.03.2013
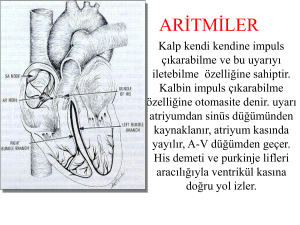
BÖLÜM 5
İDEAL AKIŞKANLARDA
MOMENTUMUN
KORUNUMU
Lineer İmpuls-Momentum Denklemi
Hareket halinde bulunan bir cismin herhangi bir andaki doğrusal hızı
V, kütlesi m olsun. Eğer dt zaman aralığında cismin hızı değişiyorsa,
cisim dengelenmemiş ΣF toplam dış kuvvetlerin etkisi altındadır. Bu
Newton’un II. kanunu olarak bilinir.
r
r d (mV)
ΣF =
dt
r
r
ΣF dt = d ( mV)
İmpuls
(5.1)
momentum (hareket miktarı)
Bir kütleye etki eden dış kuvvetlerin bileşkesi sıfır ise kütlenin
momentumu sabit kalır.
1
18.03.2013
•Boru ve kanal sistemlerindeki kıvrımların, en kesit değişimlerinin,
dallanmalarının veya akış ortamı içinde katı yüzeylerin var olduğu
yerlerde akımın hızı değişime uğrar.
•Akımın hızında doğrultu veya şiddetçe değişiklik meydana geliyorsa,
dengelenmemiş bir kuvvet söz konusudur.
•Bu kuvvet hız değişiminin meydana geldiği kısımlarda akışkana etki
eden bütün dış kuvvetlerin bileşkesi demektir.
Dengelenmemiş bileşke kuvveti oluşturan kuvvetler şunlar olabilir:
1. Akımın giriş ve çıkış kuvvetlerine etki eden basınç kuvvetleri.
2. Gerçek akışkanlar için, giriş ve çıkış kesitleri arasındaki boru veya
kanal yüzeylerinden dolayı meydana gelen sürtünme kuvveti.
3. Kütlesel kuvvet (yerçekimi kuvveti gibi).
Bir cismin hızı dt zaman aralığında V1’den V2’ye yükseliyor ise;
V2
r
ΣF ⋅ dt = m ∫ dV
V1
r
r
r
ΣF ⋅ dt = mV2 − mV1
r
r
r
ΣF ⋅ dt + mV1 = mV2
(5.2)
Bu elde edilen ifadeye “Lineer impuls momentum denklemi” denir.
Bu denklemde
r
Σ F dt = Kuvvetin dt süresi içindeki impulsu
r
m V
r
m V
1
2
= t anında m kütlesinin momentumu
= t+dt anındaki m kütlesinin momentumu
ΣF = dt zaman süresi boyunca m kütlesinin momentumunda
değişikliğe neden olan dengelenmemiş net kuvvettir.
2
18.03.2013
•Bu ifadenin akışkanlara uygulanmasında, akımın hızının değiştiği
kısımlarda bir kontrol yüzey çizilerek, elde edilen kontrol hacme
giren ve çıkan akışkan kütlesinin momentumu göz önüne alınır.
•Dikkate alınan kontrol hacminin, akışkan ortamı içinde sabit kaldığı,
yani akışkanla birlikte hareket etmediği kabul edilir.
r
∑F
K.Y
v2
V2
u2
P2
P1
2
V1
y
v1
r
V2
u1
x
1
r
r
V2 − V1
r
− V1
İmpuls momentum denklemini dt zaman süresinde giren ve çıkan
akışkan kütlesi için ifade edelim.
m giren = ρ ⋅ Q1 ⋅ dt = ρ ⋅ V1 ⋅ A1dt
m cikan = ρ ⋅ Q 2 ⋅ dt = ρ ⋅ V2 ⋅ A 2 dt
Bu ifadeler (5.2) de yerine konulursa;
r
r
r
ΣF ⋅ dt = ρ ⋅ Q 2 ⋅ V2 ⋅ dt − ρ ⋅ Q1 ⋅ V1 ⋅ dt
elde edilen bu ifade dt ile bölünürse;
r
r
r
ΣF + ρ ⋅ Q1 ⋅ V1 = ρ ⋅ Q 2 ⋅ V2
(5.3)
3
18.03.2013
Böylece akışkan akımı için impuls-momentum denklemi bulunur.
Q1= Kontrol hacme birim zamanda giren akım miktarı.
r
V1= Giriş kesitindeki hız
Q2= Kontrol hacminden birim zamanda çıkan akım miktarı.
r
V2 = Çıkış kesitindeki hız
ρ = Akışkanın özgül kütlesi
ΣF = Kontrol hacme etki eden kuvvetlerin toplamı olup, bunlar F1
giriş kesitindeki basınç kuvveti, F2 çıkış kesitindeki basınç kuvveti,
G kontrol hacim içerisindeki akışkanın ağırlığı, R reaksiyon
kuvvetidir.
Düzenli akımda kontrol yüzeyinden geçen debi sabi Q1 = Q2
olacağından (5.3) ifadesi aşağıdaki gibi yazılabilir;
r
r
r
(5.4)
ΣF = ρ ⋅ Q ⋅ V2 − V1
(
)
Skaler bileşenleri cinsinden ;
Σ F x = ρ ⋅ Q ⋅ (u
2
− u
)
v1 )
Σ F y = ρ ⋅ Q ⋅ (v
2
−
1
(5.5)
4
18.03.2013
Problemlerin Çözümü için:
1. Sistemde hızın yönünde ve şiddetinde değişiklik meydana getiren
kısmı içine alacak şekilde bir kontrol yüzeyi çizilir.
2. Kontrol yüzeyini çizdiğimiz kısım için akışkana etki eden
kuvvetler;
•Basınç ve impuls kuvvetleri giriş kesitinde çıkış doğrultusunda, çıkış
kesitinde ise akışa ters yönde
•Ağırlık kuvvetleri düşey ve aşağı yönlü yerleştirilir.
•Yatay konumda olan boru kanal kesitlerinde ağırlık kuvveti reaksiyon
kuvveti tarafından doğrudan karşılanacağından dikkate alınmayabilir.
Reaksiyon kuvveti ise herhangi bir yönde yerleştirilmelidir.
3. Bir x-y koordinat sistemi seçilir.
4. Sisteme etkili kuvvetlerin x ve y eksenleri üzerindeki izdüşümleri
alınarak impuls momentum denklemleri oluşturulur.
5. Denklemdeki bilinenler ve bilinmeyenler oluşturulur
6. Bilinmeyenler arasında Q,V,P,z,D gibi bilinmeyenler varsa
süreklilik ve Bernoulli denklemleri kullanılarak bu bilinmeyenler
hesaplanır.
7. Problemde su jeti, su fışkırtısı, su demeti, su hüzmesi gibi ifadeler
var ise basınç kuvvetleri yaklaşık olarak sıfır alınabilir. Çünkü bu tip
akımlarda akışkan en kesiti oldukça küçüktür.
5
18.03.2013
Su Jetinin Hareketli Bir Kanala veya Levhaya Çarpması Hali
Hareketli bir kanata etkiyecek kuvvetler impuls momentum
denklemleri ile hesaplanabilir
2
2
1
V2
ρQ(V-u)
1
V1
ρQ(V-u)
u
2
2
Rx
α
1
1
R
Ry
R x = ρ Q (V − u ) (1 − cos α)
R y = ρ Q (V − u ) (1 − sin α)
Burada u hareketli levhanın hızı (x yönünde)
V sistem yatay olduğundan V1=V2=V su jetinin hızı, (V-u ) su jetinin
hızı olarak tariflenir.
Kanadın yarım daire şeklinde, yani kepçe biçiminde olması halinde
V
u
V
R
İmpuls Momentum denklemi uygulanırsa, kanada etkiyen kuvvet
R = 2 ρ Q (V − u )
6
18.03.2013
Bu kepçeye çarpan jetin transfer ettiği enerji, yani güç bu kuvvetin
kepçe hızı ile çarpımından bulunur.
N=uR
N = 2 ρ Q (V − u ) u
Bu gücü maksimum yapan kepçe hızı
∂N
=0
∂u
2 ρ Q (V − u ) − 2 ρ Q u = 0
u = V/2
N max = ρ Q
V2
V2
= γQ
2
2g
Katı cisimlerin mekaniğinde bir m kütlesi V hızı ile bir levhaya
çarparsa levha hareket halinde bulunsa da bulunmasa da çarpan
cismin kütlesi değişmez.Ancak sıvıların kütlesi, hızın bir
fonksiyonu
ρ ds dA = ρ V dt dA
olduğundan impuls kuvvetindeki debi miktarı su jetinden çıkan
debiye göre farklı olacaktır. Çünkü levhayı u =V hızı ile xdoğrultusunda hareket etmesi halinde, su, bu levhaya hiç
çarpmayacaktır. O halde hareketli levhaya çarpan debi;
Q ' = (V − u ) A
7
18.03.2013
Levhaya etki eden kuvvet ise;
u
R = ρ Q ' (V − u )
A
Q
V
veya
R = ρ A (V − u ) 2
Eğer levha ters yönde hareket ediyorsa, rölatif hız =V+u. Debide
herhangi bir değişiklik olmaz ve debi; Q=V.A
Dolayısıyla impuls kuvveti
ρ Q (V + u )
8
![(Microsoft PowerPoint - B\326L\334M 5 [Uyumluluk Modu])](http://s1.studylibtr.com/store/data/000988762_1-e33fda01f39f1f6a45a09c25b7c42bd4-768x994.png)