üçgenler - WordPress.com

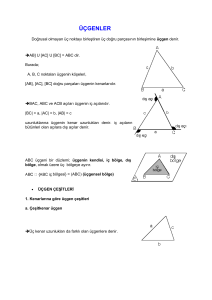
Düzlemde birbirine doğrusal olmayan üç
noktayı birleştiren, üç doğru parçasının
oluşturduğu çokgendir.
 A,B,C şeklide 3 açı(3 köşe) ve a,b,c şeklinde
3 kenardan oluşur.
GÜNÜMÜZDEN ÖRNEKLER
• Çamaşır
askısı
• Börek
• Kolye
• Trafik işareti
• Okul çantası
• Muska
ÜÇGEN ÇEŞİTLERİ
Üçgenler ikiye ayrılır
1. Kenarlarına Göre Üçgenler
 Çeşitkenar üçgen
 İkizkenar üçgen
 Eşkenar üçgen
2.Açılarına Göre Üçgenler
 Dar açılı üçgen
 Dik açılı üçgen
 Geniş açılı üçgen
örnek için
tıkla☺
örnek için
tıkla☺
Çeşit Kenar Üçgen: Üçgenin kenarlarının
hepsi farklıysa bu üçgene “Çeşit Kenar Üçgen”
denir.
İkiz Kenar Üçgen: Üçgenin kenarlarının iki
tanesi eşit olan üçgene “İkiz Kenar Üçgen” denir.
Bir ikizkenar üçgenin, taban açıların ölçüleri
birbirine eşittir.
Eşkenar Üçgen: Üçgenin kenarlarının hepsi
eşit olan üçgene “Eşkenar Üçgen” denir. Bir
eşkenar üçgenin iç açıları 60º `dir.
a
a
eşkenar
Üçgen
Çeşitkenar
Üçgen
İkizkenar
Üçgen
Dar Açılı Üçgen: Üçgenin açılarından her birinin
ölçüsü 90º`den küçük olan üçgene “Dar Açılı
Üçgen” denir.
Geniş Açılı Üçgen: Bir açısı geniş açı olan
üçgene “Geniş Açılı Üçgen” denir.
Dik Açılı Üçgen: Açılarından birisi dik açı olan
üçgene “Dik Açılı Üçgen” denir
> 90°
< 90°
Dar açılı
Üçgen
= 90°
Dik Üçgen
Geniş açılı
Üçgen
BİR ÜÇGENİN YARDIMCI ELEMANLARI
1) Üçgenin Yüksekliği: Üçgenin bir köşesinden karşı
tarafa indirilen, köşe ile kenar arasında kalan dik doğru
parçasına “Üçgenin Yüksekliği” denir.İndiği yerde 90
derecelik açı oluşur.”h” ile gösterilir.Yükseklikler dik
üçgenlerde dik açının köşesinde, geniş açılı üçgenlerde
ise üçgenin dışında kesişirler.
2.Üçgenin Kenar Ortayları: Üçgenin bir köşe ile bu
köşenin karşısındaki kenarın orta noktasını birleştiren
doğru parçasına “Üçgenin Kenar Ortayı” denir.Üçgenin
iç bölgesinde kalır. “V” ile gösterilir.
3.Üçgenin Açı Ortayı: Üçgenin açılarını iki eş açıya
bölen doğru parçasına “Üçgenin Açı Ortayı” denir. ” n ”
ile gösterilir.
 Üçgenin Kenarları Arasındaki Bağıntılar
A
a
│b-c│<a<│b+c│
│a-c│<b│a+c│
│a-b│<c<│a+b│
b
C
B
c
 Üçgende Açı Kenar Bağıntıları
A
Büyük kenarı gören açı en
büyük ,küçük kenarı gören
açı en küçüktür.Yani:
b
a
C
B
c
a<b<c ise A>B>C’ dir
A
PİSAGOR VE ÖZEL ÜÇGENLER
B
AB ve BC dik kenarlar
ve BC hipotenüstür.
AB²+ BC²=AC²
C
B
A
A
A
B
B
C
A
C
AB=7
BC=24
AC=25
C
AB=5
BC=12
AC=13
B
AB=3
BC=4
AC=5
C
AB=8
BC=15
AC=17
ÜÇGENDE ÇEVRE
 Üçgende çevre, üçgenin üç kenarının
toplanmasıyla bulunur.
Çeşitkenar üçgende çevre =a+b+c
İkizkenar üçgende çevre= a+a+b =2a+b
Eşkenar üçgende çevre=a+a+a=3a
ÜÇGENDE ALAN
Üçgende alan, bir kenar ve o kenara ait
yüksekliğin çarpımı ile bulunur.
A
A
c
h
B
a
C
A(ABC)=(a×h)/2
H
B
b
C
a
A(ABC)=(a×ha)/2=
(b×hb)2/=(c×hc)/2
İKİ ÜÇGENİN EŞLİĞİ
Kenar-Kenar-Kenar (KKK)
İki kenarı ve dahil ettikleri açı karşılıklı eş ise bu
üçgenler eştir
Kenar-Açı-Kenar (KAK)
İki açısı ve dahil ettikleri kenar karşılıklı eş ise
bu üçgenler eştir
Açı-Kenar-Açı (AKA)
Kenarları karşılıklı eş ise bu üçgenler eştir
Kenar-Açı-Açı (KAA)
İki açısı ile bunlardan birinin karşısındaki kenar
karşılıklı eş ise bu üçgenler eştir.
İKİ ÜÇGENİN BENZERLİĞİ
Açı-Açı (AA)
İkişer açılarının eş olması durumunda bu
üçgenler benzerdir
Kenar-Kenar-Kenar (KKK)
Karşılıklı kenarlarının orantılı olması durumunda
bu üçgenler benzerdir.
Kenar-Açı-Kenar (KAK)
Karşılıklı iki kenarının orantılı ve dahil ettikleri
açıların eş olması durumunda bu üçgenler
benzerdir.
D
A
B
C
E
5
F
5
m(A)=m(C)
m(B)=m(E)
m(C)=m(F)
│AB│=│DE│
│BC│=│EF│
│AC│=│DF│
ABC ile DEF üçgenleri eştir.
▲ABC≡▲DEF dir
D
A
K
L
M
3
B
C E
6
KLM İle ABC ve DEF üçgenler
benzerdir.
KLM▲≈ABC▲ ve KLM▲≈DEF▲
F
12
KAZANIMLAR
 Üçgenin iki kenar uzunluğunun toplamı veya farkı ile
üçüncü kenarının uzunluğu arasındaki ilişkiyi belirler.
Üçgenin kenar uzunlukları ile bu kenarların karşısındaki
açıların ölçüleri arasındaki ilişkiyi belirler.
Yeterli sayıda elemanının ölçüleri verilen bir üçgeni çizer.
Üçgende kenarortay, kenar orta dikme, açıortay ve
yüksekliği inşa eder.
Üçgenlerde eşlik şartlarını açıklar.
Üçgenlerde benzerlik şartlarını açıklar.
Pythagoras (Pisagor) bağıntısını oluşturur.
Dik üçgendeki dar açıların trigonometrik oranlarını belirler
KAYNAKLAR
vikipedi
www.matematikçifatih.com
MEB ilköğretim 8. sınıf matematik kitabı
8.sınıf matematik defteri
www.ekol hoca.com
www.vitaminegitim.com
HAZIRLAYAN
Gizem KUŞÇU
110404081
İlköğretim Matematik Öğretmenliği
2A(gece)