Name of presentation

Dönüş ÖZHAN
Üçgenler
Hedef: Üçgenlerde temel kavramları tanır.
Kazanımlar:
• Üçgende açı özellikleri ile ilgili işlemler yapar.
• Üçgenlerin kenar uzunlukları ile bu kenarların
karşılarındaki açıların ölçülerini ilşkilendirir.
• Uzunlukları verilen üç doğru parçasının hangi
durumlarda üçgen oluşturduklarını belirtir.
• Üçgenin yardımcı elemanlarını belirtir.
ÜÇGENLER
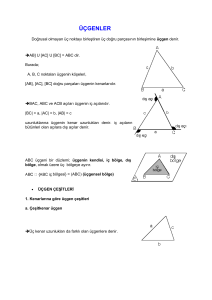
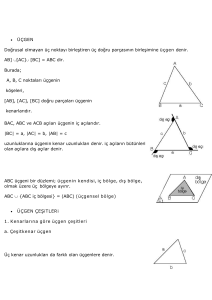
Üçgen: Doğrusal olmayan üç noktandan oluşan geometrik şekile üçgen denir.
A, B, C bir üçgen olmak üzere,
M, A, C doğrusal,
A, B, K doğrusal,
B, C, L doğrusaldır.
x, y ve z üçgenin iç açıları β, θ ve α
üçgenin dış açılarıdır.
Herhangi bir üçgende,
x + y + z = 180°
β + θ + α = 360° ‘dir.
A)20
B)30
C)40
D)50
E)60
Çözüm:
Üçgen Çeşitleri
a) Açılarına Göre Üçgenler
Dar açılı üçgenler: İç açılarının her biri 90° ’den küçük olan
üçgenlerdir.
Geniş açılı üçgenler: İç açılarının herhangi birinin ölçüsü
90° ‘den büyük olan üçgenlerdir.
Uyarı: Bir üçgende yalnız bir tane geniş açı olur.
Dik açılı üçgenler: Bir açısının ölçüsü 90° olan üçgenlere
denir.
Uyarı: Bir üçgende yalnız bir tane dik açı olur.
b) Kenarlarına göre üçgenler
İkiz kenar üçgen: İki kenar uzunluğu birbirine eşit olan üçgenlere
.
ikiz
kenar üçgen denir.
ABC ikiz kenar üçgeninde,
|AB|=|AC| olduğundan bu kenarları gören
taban açılarıda birbirine eşittir.
m(ABC)=m(ACB)= α ve tepe noktası
m(BAC)= β ‘dir.
Örnek:
.
Çözüm: Şekilde görüldüğü gibi ABD üçgeni ikiz kenar
olduğundan D açısı 40°, açısı iki iç açının toplamı kendisine
komşu olmayan bir dış açıya eşit olduğundan 40°+40°=80° dir.
|AD|=|AC| olduğundan C açısı 40° dir. Üçgenin iç açıları toplamı
180° olduğundan,
x+ 40°+ 80°= 180°
x+120°= 180°
x= 180°- 120°
x= 60°
.
Eşkenar üçgen: Bütün kenar uzunlukları birbirine eşit olan
üçgenlere eşkenar üçgen denir. Eşkenar üçgenlerin bütün açı
ölçüleri eşit olup 60° ‘dir.
Çeşit kenar üçgen: Bütün kenar uzunlukları birbirinden farklı
olan üçgenlere çeşitkenar üçgen denir.
Üçgen İle İlgili Özellikler
1. Herhangi bir üçgende iki iç açının ölçüsü toplamı kendisine
komşu olmayan bir dış açıya eşittir.
2.
Örnek:
A)40
Çözüm:
B)50
C)60
D)70
E)80
Üçgende Açı Kenar Bağıntıları
1. Bir üçgende büyük açı karşısında büyük kenar, küçük açı karşısında küçük kenar
eşit açılar karşısında eşit kenarlar bulunur.
Bir ABC üçgeninde,
|AB|>|BC|>|CA| ise m(C)>m(A)>m(B) olur.
Terside doğrudur. Eğer
m(C)>m(A)>m(B) ise |AB|>|BC|>|CA| olur.
Örnek:
Çözüm: ABC üçgeninde ACB açısını ölçüsü 61° ve ADC açısının
ölçüsü 80° derecedir. ADC üçgeninde 80° karşılık gelen kenar ACB
üçgeninde 60° ‘ye karşılık geldiği için ACB üçgeni ADC üçgeninden
büyüktür. ACB üçgeninde en büyük açı C açısı olduğundan buna
karşılık gelen kenarda en uzun kenardır yani a kenarıdır.
2. Bir üçgende herhangi bir kenar diğer iki kenarın uzunlukları
toplamından küçük, farklarının mutlak değerinden büyük olmak
zorundadır.
Örnek:
Çözüm:
x’ in alabileceği değerler,
|8-5|<x<8+5 ve |5-4|<x<5+4 arasındadır.
3<x<13 ve 1<x<9 olduğundan
3<x<9 değerleri iki aralığıda sağlar. Bu
değerlerin toplamı ise
4+5+6+7+8= 30 olur.
Not: Bir ABC üçgeninde,
a) Dik kenarların kareleri toplamı, 90° karşısındaki kenarın
karesine eşittir.
m(B)= 90° ise
a²+c² = b² olur.
(Pisagor bağıntısı)
b) Eğer ABC dar açılı bir üçgen ve m(B)<90° ise a²+c² > b² olur.
A
B
C
c) Eğer ABC geniş açılı bir üçgen ve m(B)>90° ise b² > a²+c² olur.
A
B
C
Üçgenin Elemanları
1. İç açıortay: Bir üçgenin bir iç açısını iki eşit parçaya ayıran ışının
karşı kenara değdiği nokta ile köşe arasında kalan doğru parçasına
üçgende iç açıortay denir.
2. Dış açıortay: Bir üçgenin bi dış açısını iki eşit parçaya ayıran ışının
karşı kenarın uzantısının değdiği nokta ile köşe arasında kalan
doğru
parçasına üçgenin dış açıortayı denir. [AN] dış açı ortay olup ile gösterilir.
3. Kenar ortay: Bir üçgende bir kenarın orta noktasını karşı köşeye birleştiren
doğru parçasına bu kenara ait kenar ortay denir.
4. Yükseklik: Bir üçgende bir köşeden karşı kenara çizilen dikmenin köşe ile
kenar arasında kalan parçasına bu kenara ait yükseklik denir.
Örnek:
Çözüm:
2ç+2d=180°
2a+2e=180°
ç+d=90°
a+e=90°
Dötgenin iç açıları toplamı 360°
olduğundan,
ç+d+a+e+2x+65° +4x-5° = 360° dır.
90°+90°+60°+6x=360°
6x=120°
x=20°
2x+65 ° +d+e=180°
2.20° +65° +d+e=180°
105° +d+e=180°
d+e=180° -105°=75°
d+e=75° ise 2d+2e=150°
m(A)+150° =180°
m(A)=180° -150° =30°