Slide 1 - Ninova
advertisement
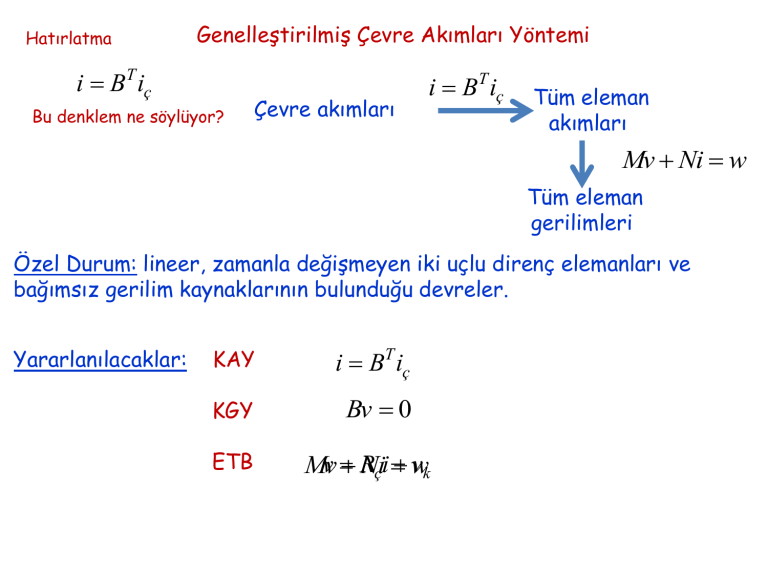
Hatırlatma Genelleştirilmiş Çevre Akımları Yöntemi i BT iç Bu denklem ne söylüyor? Çevre akımları i BT iç Tüm eleman akımları Mv Ni w Tüm eleman gerilimleri Özel Durum: lineer, zamanla değişmeyen iki uçlu direnç elemanları ve bağımsız gerilim kaynaklarının bulunduğu devreler. Yararlanılacaklar: KAY i BT iç KGY Bv 0 ETB v R vk Mv Niçi w Yöntem: Hatırlatma Bv 0 2. Adım: eleman tanım bağıntılarını yerleştir Bv 0 B[ Rçi vk ] 0 1. Adım: ne nd 1 göz için KGY’ını yaz BRçi Bv k 0 BRçi Bv k 3. Adım: eleman akımlarını çevre akımları cinsinden yaz i BT iç 4. Adım: çevre akımlarını bul BRç BT iç Bvk ˆ i v R ç ç b kontrollü elemanları Genel Durum: lineer, lineer,zamanla zamanladeğişmeyen değişmeyenakım iki uçlu dirençdirenç elemanları bağımsız gerilim kaynakları Birinci grup elemanlar akımuçlu kontrollü direnç lineer, zamanla değişmeyen çok dirençolmayan elemanları elemanlarıakım kaynakları bağımsız İkinci grup elemanlar bağımsız akım kaynakları Yöntem: Hatırlatma 1. Adım: ne nd 1 göz için KGYı’nı yaz Bv 0 v1 [ B1 B2 ] 0 v2 2. Adım: 1. grup elemanların eleman tanım bağıntılarını yerleştir, 2. grup elemanların eleman tanım bağıntılarını yaz. [ B1R1 i1 B2 ] B1vk v2 v2 [ M N ] w i2 3. Adım: eleman akımlarını çevre akımları cinsinden yaz i1 B1T iç i2 B2T iç B1R1B1T T NB 2 B2 iç B1vk M v2 w 4. Adım: çevre akımlarını ve ikinci grup elemanların gerilimlerini bul Toplamsallık ve Çarpımsallık Özelliği Teorem: (Toplamsallık) 1. Grup bağımsız kaynaklar 2. Grup bağımsız kaynaklar Lineer direnç elemanları+Bağımsız kaynaklar 1. Grup bağımsız kaynaklar devrede, 2. grup bağımsız kaynaklar devre dışı iken devre çözülsün i1,v1 2. Grup bağımsız kaynaklar devrede, 1. grup bağımsız kaynaklar devre dışı iken devre çözülsün i2 ,v2 Devrede tüm bağımsız kaynaklar varken ki çözüm Tanıt: w w w , Devrede ki tüm bağımsız kaynakları T 1 2 A 0 M 0 I N 0 iT 0 AT vT 0 0 eT wT ~ A x bT ~ xT A 1bT iT A v 0 T eT M 0 I N iT i1 i2 , vT v1 v2 0 AT 0 1 ~ 1 0 0 xT A w1 w2 0 0 wT 1. Grup bağımsız kaynaklar devrede A 0 M 0 I N 0 i 0 AT v 0 0 e w1 ~ A x b1 ~ x1 A 1b1 i1 A v 0 1 e1 M 0 I N 1 0 0 w1 1 0 0 w2 0 AT 0 ~ 1 0 x1 A w1 2. Grup bağımsız kaynaklar devrede A 0 M 0 I N 0 i 0 AT v 0 0 e w2 i1 A v 0 1 e1 M 0 I N ~ 1 0 x2 A w2 ~ 1 0 ~ 1 0 ~ 1 0 0 x1 x2 A A A xT w1 w2 w1 w2 ~ A x b2 ~ 1 x1 A b2 0 AT 0 Teorem: (Çarpımsallık) Lineer direnç elemanları+Bağımsız kaynaklar i, v var iken devre çözülsün Lineer direnç elemanları+Bağımsız kaynakların değeri k katına çıkarılsın ve devre çözülsün ~ i ki v~ kv ~~ i ,v Thevenin (1883) ve Norton (1926) Teoremleri Amaç: Lineer, zamanla değişmeyen çok uçlu, iki uçlu dirençlerden ve bağımsız akım ve gerilim kaynaklarından oluşmuş bir N 1-kapılısının basit bir eşdeğerini elde etmek. Thevenin Eşdeğeri: i R TH i + N 1-Kapılısı v _ + _ + VTH v _ RTH + _ RTH Thevenin eşdeğer direnci i + v VTH _ Devredeki tüm bağımsız kaynaklar devre dışı iken 1-1’ uçlarından görülen eşdeğer direnç VTH Açık devre gerilimi 1-1’ uçları açık devre iken 1-1’ uçları arasındaki gerilim Thevenin Teorem: N 1-kapılısının uçlarına i değerinde bir akım kaynağı bağlandığında tüm i değerleri için tek çözümü varsa ( tek v değeri belirlenebiliyorsa) Thevenin eşdeğeri vardır. Norton Eşdeğeri: i + N 1-Kapılısı v _ i + iN GN v _ i GN Norton eşdeğer iletkenliği + iN GN v _ Devredeki tüm bağımsız kaynaklar devre dışı iken 1-1’ uçlarından görülen eşdeğer iletkenlik iN Kısa devre akımı 1-1’ uçları kısa devre iken 1-1’ uçlarındaki akım Norton Teorem: N 1-kapılısının uçlarına v değerinde bir gerilim kaynağı bağlandığında tüm v değerleri için tek çözümü varsa ( tek i değeri belirlenebiliyorsa) Norton eşdeğeri vardır. • Thevenin Eşdeğeri: v(t ) RTH i(t ) vTH (t ) N kapılısı akım kontrollü değilse Thevenin eşdeğeri yok • Norton Eşdeğeri: i(t ) GN v(t ) iN (t ) N kapılısı gerilim kontrollü değilse Norton eşdeğeri yok • • RTH 0, v 0 GN 0, i 0 vTH (t ) RTH 0, Norton eşdeğeri yok RTH i (t ) G 0, Thevenin eşdeğeri yok vTH (t ) N N GN iN (t ) v (t ) v (t ) v (t ) vTH iN i (t ) iN i (t ) i (t ) vTH Sonuç: • Lineer, zamanla değişmeyen direnç ve bağımsız kaynaklardan oluşmuş N 1-kapılısı akım kontrollu ise bağlı bulunduğu devrenin çözümünü etkilemiyecek şekilde Thevenin eşdeğeri ile ifade edilir. •Lineer, zamanla değişmeyen direnç ve bağımsız kaynaklardan oluşmuş N 1-kapılısı gerilim kontrollu ise bağlı bulunduğu devrenin çözümünü etkilemiyecek şekilde Norton eşdeğeri ile ifade edilir. Eleman Tanım Bağıntıları f R (v, i, t ) 0 v i fC (v, q, t ) 0 q i q v f m ( , q, t ) 0 memristor endüktans Kapasite direnç f L ( , i, t ) 0 Ø Direnç Elemanı: v ve i arasında cebrik bağıntı ile temsil edilen eleman Endüktans Elemanı: Ø ve i arasında cebrik bağıntı ile temsil edilen eleman Kapasite Elemanı: v ve q arasında cebrik bağıntı ile temsil edilen eleman Memristor Elemanı: Ø ve q arasında cebrik bağıntı ile temsil edilen eleman