Deney No: 1
Deneyin Adı: Ölçü Aletlerinin Tanıtılması
Deneyin Amacı: Breadboard üzerinde devre kurma alışkanlığı kazanmak ve elektrik
devrelerindeki akım, gerilim, direnç gibi fiziksel büyüklükleri ölçmeyi öğrenmek
Önbilgi
1.Deney Ekipmanlarının Tanıtılması
a) Breadboard
Breadboard, elektrik devrelerinin üzerine kurulmasını sağlayan en temel deney ekipmanıdır.
Fotoğraf 1-a ve 1-b’de breadboard’un sırasıyla dıştan ve içten görünümü görülmektedir.
Breadboard dıştan, 1-30’a kadar rakamlar ve a-j’e kadar sayılarla satır ve sütun numarası
tanımlı, çok sayıda delikten oluşan dışı plastik kaplı bir devre ekipmanıdır. Fotoğraf 1-b’de
görülen iç yapısına bakıldığında ise; dıştan görülen delikleri elektriksel olarak birbirine
bağlayan birçok metal parçada oluştuğu görülmektedir. Bu parçalar, delikten sokulacak telleri
sıkıca yerinde tutacak şekillerde üretilmiş ve plastiğin içerisine sağlamca yerleştirilmişlerdir.
Fotoğraf 1: a) Breadboard’un Dıştan Görünümü, b) Breadboard’un İç Yapısı
Breadboard üzerindeki delikler yatay ve dikey olarak kısa devre edilmiştir. Fotoğraf 1-a’ da
görüldüğü gibi breadboard harflerden (a,b,c,d,e,f,g,h,i,j) oluşan satırlara ve (1,2,…30)
rakamlardan oluşan sütunlara ayrılmıştır. Ortada görülen deliklerden aynı rakam numarasına
sahip fakat farklı harf numarası bulunan 5’er delikler kendi arasında yatay olarak kısa
devredir. Örneğin; a1, b1, c1, d1, e1 aynı rakam numaralı dolayısıyla aynı hat üzerinde
bulunmaktadır.
Sayfa - 1 -
Toplam Sayfa - 21 -
b) DC Güç Kaynağı
DC güç kaynakları, elektronik devrelerin çalıştırılması için zamana bağlı olarak yönü ve
şiddeti değişmeyen elektriksel sinyal üretirler. DC güç kaynağının vermesini istediğimiz,
gerilim değeri, kaynağın üzerinde yer alan ayar düğmesi ayarlanır. Ayarlanan gerilim ve
kaynağın çektiği akım değerleri dijital ekranda gözlemlenir. Ayarlanabilir gerilim, -30V <
Vistenen <+30 V ise analog devre tasarımlarında kullanılır. Güç kaynağının sabit gerilimi (+ 5
V) TTL devre tasarımlarında kullanılır.
Fotoğraf 2: DC Güç Kaynağı
Şekil 1: a) DC Gerilim Sinyali, b) DC Akım Sinyali
c) İşaret Üreteci (Fonksiyon Jeneratörü)
İşaret üreteci, belirli alt ve üst sınırlar içerisinde, istenilen genlik ve frekans değerinde
sinüs, kare, üçgen gibi dalga şekillerini üretebilir.
Sayfa - 2 -
Toplam Sayfa - 21 -
Fotoğraf 3: Fonksiyon Jeneratörü
d) Multimetre
Akım, gerilim ve direnç ölçümü gibi temel ölçümlerin yanında kapasitans, endüktans,
diyot, transistör, frekans ve iletkenlik gibi elektriksel büyüklükleri de ölçebilen ölçü aletine
Multimetre denir. Multimetreler, analog ve sayısal olmak üzere iki çeşittir. Ölçülen değeri bir
ölçek üzerinde sapabilen ibre (ya da benzeri bir mekanik hareket) ile gösteren ölçü aletine
analog multimetre denir. Ölçülen değeri sayısal bir gösterge üzerinde sayısal olarak gösteren
ölçü aletine ise digital multimetre denir.
Fotoğraf 4: a) Analog Multimetre b) Digital Multimetre
Sayfa - 3 -
Toplam Sayfa - 21 -
Multimetre Ayar Düğmeleri
Şekil 2: a) Multimetre Elektriksel Büyüklük ve Kademe Ayarı Seçim Kısmı
OFF konumu
Cihazı kapatmak için kullanılır.
mA konumu
1.İşlevi: AC akım (mili amper mertebesinde)
ölçmek için kullanılır.
2.İşlevi: DC akım (mili amper mertebesinde)
ölçmek için kullanılır.
V konumu
1.İşlevi: AC gerilimi ölçer.
2.İşlevi: DC gerilimi ölçer.
20A konumu
1.İşlevi: AC akım (amper mertebesinde)
ölçmek için kullanılır.
2.İşlevi: DC akım (amper mertebesinde)
ölçmek için kullanılır
Ω/Buzzer konumu
1.İşlevi: Direnç ölçmek için kullanılır.
2.İşlevi: Kısa devre testi (Buzzer).
Hz konumu
Frekans ölçmek için kullanılır.
Diyot/C konumu
1.İşlevi: Diyot eşik gerilim değerini ölçer.
2.İşlevi: Kondansatör kapasite değerini ölçer.
Şekil 3: Multimetrede Ölçüm Problarının Bağlantı Şeklinin Gösterimi
Amper mertebesinde akım ölçmek için
kullanılır.
Referans ucu takmak için kullanılır.
Akım ölçümü haricinde multimetre ile
Miliamper mertebesinde akım ölçmek
ölçülebilen
diğer bütün büyüklükleri ölçmek
için kullanılır.
için kullanılır. (V,R,Hz gibi…)
Sayfa - 4 -
Toplam Sayfa - 21 -
2.Gerilim, Akım ve Direnç Ölçümü
Gerilim nasıl ölçülür?
1.Voltmetre, gerilimi ölçülecek devre elemanı ile paralel bağlanır.
Şekil 4: Voltmetre ile gerilim ölçmek için bağlantı şekli
2. DC gerilim ölçümünde yön önemlidir. Her şeyden önce hatalı bağlantı ile Kirchhoff’un
kanunlarına aykırı bir iş yapıldığı için yönler dikkate alınarak bağlanmalıdır. Ters yönde de
sapabilen analog ölçü aletleri mevcut olmasına karşın; Bazı analog voltmetrelerde,
voltmetrenin ölçüm uçları ter yönde sapma özelliğine sahip değildir. İbre ters yönde sapmaya
zorlanırsa, bunun sonucunda ibre eğrilebilir ya da ölçü aleti zarar görebilir.
3. AC gerilim ölçümlerinde voltmetrenin bağlanma yönü önemli değildir.
4. Ölçü aleti üzerinde gerilim ölçümü için mevcut olan uygun test soketlerinin kullanılması
gerekir. Örneğin gerilim ölçümü için gerilim test soketi gb.
5. AC veya DC ölçümün hangisi yapılıyorsa, fonksiyon seçme anahtarlarının bunlara uygun
konumlarda olması gereklidir. AC gerilim ölçümü yaparken DC kademede ise ortalama
değeri gösterir. AC kademede iken gerilimin efektif (etkin) değerini gösterir.
6. Ölçüm aralığı seçme anahtarlarının uygun konumlarda olması gereklidir. Eğer ölçülecek
değer tam olarak bilinmiyorsa, tahmin edilen değerin bir üst kademesine getirilerek ölçüme
başlanmalıdır. Ölçülen kademede okunan değer, ancak ve ancak alt kademenin en büyük
değerinden küçükse, hassas okuma yapmak için daha sonra alt kademeye getirilebilir. Bu
ayarlamaların uygun yapılmaması durumunda ölçü aleti zarar görebilir.
Akım nasıl ölçülür?
1.Ampermetre, akımı ölçülecek devre elemanına seri bağlanır.
Sayfa - 5 -
Toplam Sayfa - 21 -
Şekil 5: Ampermetre ile akım ölçmek için bağlantı şekli
2. DC akım ölçülürken yön önemlidir. Her şeyden önce hatalı bağlantı ile Kirchhoff’un
kanunlarına aykırı bir iş yapıldığı için yönler dikkate alınarak bağlanmalıdır. Analog DC
ampermetre de akım yönüne duyarlıdır. Ters bağlantı yapıldığında ibre ters yöne sapar.
Sayısal ampermetrelerde ise ters bağlantı durumunda göstergede akım değerinin başında eksi
işareti okunur, fakat ölçü aleti hasar görmez.
3. AC akım ölçümlerinde ampermetrenin bağlanma yönü önemli değildir.
4. Ölçü aleti üzerinde akım ölçümü için mevcut olan uygun test soketlerinin kullanılması
gerekir. Sadece akım ölçümü için ayrılan soketler kullanılmalıdır.
5. Ölçüm aralığı seçme anahtarlarının uygun konumlarda olması gereklidir. Eğer ölçülecek
değer tam olarak bilinmiyorsa, tahmin edilen değerin bir üst kademesine getirilerek ölçüme
başlanmalıdır. Ölçülen kademede okunan değer, ancak ve ancak alt kademenin en büyük
değerinden küçükse, hassas okuma yapmak için daha sonra alt kademeye getirilebilir. Bu
ayarlamaların uygun yapılmaması durumunda ölçü aleti zarar görebilir.
6. AC veya DC ölçümün hangisi yapılıyorsa, fonksiyon seçme anahtarlarının bunlara uygun
konumlarda olması gereklidir. AC akım ölçümü yaparken DC kademede ise ortalama değeri
gösterir. AC kademede iken akımın efektif (etkin)değerini gösterir.
7. Güç kaynağı açılır ve akımın geçtiği yöne göre (+) ya da (–) değer okunur. Elde edilen
değer (-) ise ve böyle bir bağlantı deney sorumlusu tarafından istenmemişse hatalı bir bağlantı
yapmışsınızdır. Ampermetre uçları güç kaynağı kapatılarak değiştirilmelidir.
Direnç nasıl ölçülür?
Elektriksel direnç Ohmmetre ile ölçülür. Ohmmetre olarak Avometre veya SMM kullanılır.
Direnci ölçülecek olan elemanın devre ile bağlantısının olmaması gerekir, en azından bir
ucunun boşta olması gereklidir. Ohmmetre ile direnç ölçümü için sırasıyla aşağıdaki
kurallar uygulanmalıdır:
1. Analog Ohmmetre ile ölçüm yapılacak ise, önce Ohmmetrenin ölçüm uçları birbirlerine
değdirilerek ibrenin sıfır ohm gösterecek şekilde sapıp sapmadığı kontrol edilir. Ohmmetre
pilinin kuvvetli ya da zayıf olmasına göre ibre sıfır ohm’un biraz sağında veya solunda
Sayfa - 6 -
Toplam Sayfa - 21 -
olabilir. İbre tam sıfır ohm çizgisi üzerinde değilse, ibreyi sıfır ohm çizgisi üzerine getirmek
için sıfır ayar vidası ile ayar yapılır.
2. Sayısal Ohmmetre ile ölçüm yapılacak ise, Ohmmetrenin doğru çalışıp çalışmadığından
anlamak için aşağıdaki işlemleri yapılır. Ohmmetrenin uçları açık iken göstergenin sol
tarafında yanıp sönen “1” sayısının olduğundan ve “Low Batt” mesajının görünmediğinden
emin olunuz. Göstergedeki yanıp sönen “1” sayısı Ohmmetrenin o anda ölçtüğü direncin
sonsuz (yani açık devre) olduğunu belirtir. Daha sonra Ohmmetrenin uçlarını birbirine
birleştirilir. Bu durumda göstergede çok küçük değerde bir reel sayı okunacaktır. Bu reel sayı,
ölçü aletinin ve ölçü aleti kablolarının toplam iç direncidir. Göstergede bunlardan farklı
değerler görünmesi durumunda ölçü aletiniz bozulmuş veya pili zayıflamış olabilir.
3. Uygun bir ohm kademesi seçilir. Eğer direnç değeri bilinmiyorsa, en yüksek kademeden
başlanarak uygun konumuna gelinceye kadar kademe azaltılır.
Şekil 6: Eşdeğer Direnç Ölçümü İçin Örnek Bağlantı Şekli
4. Ohmmetrenin ölçüm uçları direncin iki ucuna sıkıca temas ettirilir. Ölçüm sırasında, ölçüm
yapan kişi direncin bir ucundan tutabilir, fakat direncin iki ucundan da tutması durumunda
kendi vücut direnci de ölçülen direnç ile paralel bağlı olacağından hatalı ölçüm yapılmış olur.
5. Bazı sayısal Ohmetreler doğrudan değeri göstermez. Bu durumda kademenin yanında
yazan bir çarpan ile çarpılarak gerçek direnç değeri bulunur.
6. Dirençler üzerlerindeki değerde olmazlar. Dirençlerin gerçek değerlerinin Ohmmetre ile
ölçülmesi gerekir. Dirençlerin tolerans değerlerinin olması, teorik ve pratik sonuçlarda
farklılığa neden olan sebeplerden biridir.
7. Laboratuarda özellikle deney sorumlusu bir asistan yanınızda yokken, gerilim vererek ölçü
aletlerini öğrenmeyi deniyorsanız, kendinize ve cihazlara zarar verememek için hem KΩ
mertebesinde dirençler kullanmanız hem de küçük küçük gerilimlerle (örneğin 1V,5V..10V
gibi) çalışarak, devrenizden mA seviyesinde akımlar geçirmeniz istenmektedir. Örneğin
10V’luk bir gerilim kaynağına 1 Ω’luk seri bir direnç bağlarsanız, devreden 1 A gibi büyük
bir akım geçer. Böyle bir durumda ilk olarak, laboratuardaki dirençlerin gücü P=V.I=10W
olmadığı için hemen bozulacak veya yanacaktır. İkinci olarak eğer devrede bir ölçü aletinizde
varsa ve en yüksek kademede değilse o da zarar görecektir.
Direnç Renk Kodları
Direnç değerleri, ölçü aleti kullanmadan üzerindeki renklerin kodları kullanarak da
hesaplanabilir. Karbon dirençler üzerindeki renk bantları Şekil 7’de gösterilmiş, renk kodları
Tablo 1’de verilmiştir. Şekil 7’de görüldüğü gibi, dört renk bandından üçü (A, B ve C)
Sayfa - 7 -
Toplam Sayfa - 21 -
birbirine yakın, dördüncüsü (T) bu gruptan biraz uzaktır. A, B ve C renk bantları direncin
değerini tanımlar, T renk bandı ise direncin toleransını tanımlar.
Direncin toleransı, üretim hataları nedeniyle direnç değerinin üzerinde yazılı olan değerden
yüzde kaç farklı olabileceğini (beklenen değerden sapma miktarını) gösterir. Örneğin, 100’luk
bir direncin toleransı ±%5 ise, direncin değeri büyük bir olasılıkla 95 ile 105 Ω arasındır.
Şekil 7: Karbon Direnç Renk Bantları
Tablo-1: Direnç Renk Kodları
İpucu: En kolay ezberleme yollarından birisi, ezberlemek istediğimiz olay ya da durumu
kolayca hatırlayacağımız başka bir şeye benzemektir. Direnç renk kodlarını aklımızda tutmak
için,
“SO.KA.K.TA
SA.YA.MA.M”
sihirli
sözcüğünü
kullanabiliriz.
Sayfa - 8 -
Toplam Sayfa - 21 -
Deney No: 2
Deneyin Adı: Kirchoff’un Akım ve Gerilimler Yasası
Deneyin Amacı:
* Kırchoff’un akımlar ve gerilimler yasasını öğrenmek ve bread board üzerinde kurulan basit
elektrik devreleri yardımıyla bu yasaları pekiştirmek
* Direnç, diyot ve zener diyot gibi devre elemanlarının Akım-Gerilim öz eğrilerini çıkararak
elemanların karakteristik özelliklerinin anlaşılması
Önbilgi
Kırchoff’un Akımlar ve Gerilimler Yasası’nı daha iyi anlayabilmek için öncelikle çevre ve
düğüm kavramlarından bahsedilmelidir.
Düğüm: Bir devrede dolaşan akımın iki veya daha fazla parçaya bölündüğü her nokta, düğüm
olarak adlandırılır.
Çevre: Bir elektrik devresinde herhangi bir noktadan başlayıp tekrar aynı noktaya gelinceye
kadar devrede dolaşılan kapalı yola çevre denir.
Şekil-1: DC Beslemeli Bir Elektrik Devresinde Kapalı Çevrelerin Ve Düğüm Noktalarının
Gösterilmesi
1.Kırchoff’un Akımlar Yasası (KCL)
Bu yasaya göre herhangi bir düğüm noktasına gelen akımların toplamı, düğüm noktasından
çıkan akımların toplamına eşittir. Şekil-1’deki her bir düğüme ilişkin düğüm denklemlerini
(D1, D2, D3 ve D4) Tablo-1’de görmekteyiz.
Tablo-1: Şekil-1’de Verilen Devre İçin Düğüm Denklemleri
Düğüm
Düğüme Giren
Düğümden
Düğüm
Numarası
Akımlar
Çıkan Akımlar
Denklemi
1
I1
I2 ve I3
I1=I2+I3
2
I2
I4 ve ı5
I2=I4+I5
3
I3 ve I4
I6
I3+I4=I6
4
I5 ve I6
I7
I5+I6=I7
*Metni yazın+
2. Kırchoff’un Gerilimler Yasası (KVL)
Bir elektrik devresinde kapalı bir çevre içerisinde gerilimlerin toplamı sıfıra eşittir. Diğer
bir ifadeyle kapalı bir çevrede, kaynağın sağladığı gerilim, elemanlar (R, L ve C vs.) üzerinde
harcanan gerilim değerlerinin toplamına eşittir. Şekil-1’deki her bir kapalı çevreye ilişkin
(Ç1, Ç2 VE Ç3) çevre denklemlerini Tablo-2’de görmekteyiz.
Tablo-2: Şekil-1’de Verilen Devre İçin Çevre Denklemlerinin Elde Edilmesi
Çevre (Döngü) Çevrede Yer
Çevrede Yer
Düğüm
Numarası
Alan Gerilim
Alan Dirençler Denklemi
Kaynağı
1
E
R1,R2,R5
E=V1+V2+V5
2
R2,R3,R4
V3=V2+V4
3
R4,R5,R6
V5=V4+V6
Doğrusal Direncin Akım-Gerilim Öz eğrisinin Çıkarılması
Zamana bağlı olarak değeri değişmeyen, içinden geçen akım ile uçları arasındaki gerilim
düşümü arasındaki ilişki doğrusal olan devre elemanıdır. Doğrusal dirençlerde, direncin
üzerindeki gerilim düşümü arttığında orantılı olarak uçlarından geçen akımında artar
dolayısıyla R= V/I denkleminden direnç değeri her t anı için sabit kalır (Şekil 2-b).
(a)
(b)
Şekil-2: (a) Doğrusal Direncin Simgesi ve (b) Akım-Gerilim Özeğrisi
*Metni yazın+
Deney No: 3
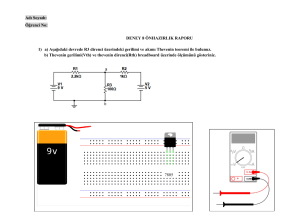
Deneyin Adı: Thevenin ve Norton Teoremi
Deneyin Amacı: Deneyin amacı, elektrik devrelerinin çözümlenmesinde kullanılan önemli
teoremlerden olan Thevenin ve Norton teoremlerinin deneysel olarak incelenmesidir.
Önbilgi
1.Thevenin Teoremi
Thevenin Teoremi, karmaşık bir devrede herhangi iki nokta arasında akan akım veya
gerilim hesaplanmak istenildiğinde ilgili devrenin daha basit çözümlenmesini sağlar. Bunun
için devre, Thevenin eşdeğer devresi denilen çok daha basit bir devreye dönüştürülür. Seçilen
uçlar arası açık devre düşünülerek, uçlar arasındaki açık devre gerilimi (Vth) ve eşdeğer
direnç (Rth) bulunarak iki nokta arasında görülen devre seri bağlı bir direnç (Rth) ve bir
gerilim kaynağı (Vth) ile ifade edilir (Şekil1).
Şekil 1:Thevenin Eşdeğer Devresi
Örnek Uygulama
Thevenin Teoremi, Şekil 2’de verilen örnek devre için adım adım uygulanırsa;
Şekil 2:Thevenin Teoremi uygulanacak örnek devre
1.Devrede bağımsız kaynaklar iptal edilerek (Akım kaynakları açık devre, gerilim kaynakları
kısa devre yapılır.) A-B uçları arasında görülen eşdeğer direnç (Rth) bulunur.
*Metni yazın+
Şekil3: 2’de verilen örnek devrenin 1. Adım uygulanmış şekli
2. Devre tekrar eski haline dönüştürülerek gerilim bölme kuralı yada ohm kanunu kullanılarak
A-B uçları arasında görülen açık devre gerilimi Vth bulunur.
Şekil4:2’de verilen örnek devrenin 2. Adım uygulanmış şekli
3. Bulunan Rth, Vth değerleri ve akım, gerilim (IL ve VL) değerleri bilinmek istenen RL
kullanılarak Thevenin Eşdeğer Devresi çizilir.
Şekil5: 2’de verilen örnek devrenin Thevenin Eşdeğer Devresi
2.Norton Teoremi
Norton Teoremi, Thevenin teoremine benzer şekilde seçilen iki
devrenin basitleştirilmesi esasına dayanır. Norton teoreminde farklı
üzerinden gidilir. Seçilen uçlar arası (A-B) kısa devre düşünülerek,
devre akımı (IN) ve eşdeğer direnç (RN) bulunarak iki nokta arasında
bağlı bir direnç (RN) ve bir akım kaynağı (IN) ile ifade edilir (Şekil6).
*Metni yazın+
uç arasında yer alan
olarak çözüme akım
uçlar arasındaki kısa
görülen devre paralel
Şekil 6: Norton Eşdeğer Devresi
Örnek Uygulama
Thevenin Teoremi uyguladığımız 2’de verilen örnek devre için Norton Teoremi uygulanırsa;
1. Devrede bağımsız kaynaklar iptal edilerek (Akım kaynakları açık devre, gerilim kaynakları
kısa devre yapılır.) A-B uçları arasında görülen eşdeğer direnç (RN) bulunur.
Şekil 7: 2’de verilen örnek devrenin 1. Adım uygulanmış şekli
2. Devrede yer alan bağımsız kaynak tekrar eski haline dönüştürülür ve A-B uçları arası kısa
devre yapılır.Bu durumda A-B uçları arasında görülen kısa devre akımı IN bulunur.
Şekil 8: 2’de verilen örnek devrenin 2. Adım uygulanmış şekli
A-B uçlarının kısa devre edilmesi 100 ohm’luk iki direncinde kısa devre edilmesi anlamına
gelmektedir. Bu durumda kısa devre yolundan akacak akım sadece 25’er ohm’luk iki seri
dirençten geçecek ve değeri IN=100V/50Ω=2A olacaktır.
3. Bulunan RN, VN değerleri ve akım, gerilim (IL ve VL) değerleri bilinmek istenen RL
kullanılarak Norton Eşdeğer Devresi çizilir.
*Metni yazın+
Şekil 9: 2’de verilen örnek devrenin Norton Eşdeğer Devresi
*Metni yazın+
Deney No: 4
Deneyin Adı: Devre Çözümlenmesinde Toplamsallık (Süperpozisyon) Teoremi
Deneyin Amacı: Deneyin amacı, elektrik devrelerinin çözümlenmesinde kullanılan önemli
teoremlerinden biri olan Toplamsallık teoreminin deneysel olarak incelenmesidir.
Önbilgi
Birden çok bağımsız kaynağın bulunduğu lineer bir devrede, herhangi bir elemana ilişkin
akım veya gerilim değeri; bağımsız kaynakların her birinin teker teker yapmış oldukları
katkıların toplamına eşittir.
Süperpozisyon ilkesini uygulamak için;
1. Devredeki gerilim veya akım kaynaklarından herhangi birisi seçilir. Bu sırada diğer
kaynaklar yok edilir (Gerilim kaynakları kısa devre, akım kaynakları açık devre yapılır).
2. İlgilenilen devre elemanlarına ilişkin akım ve gerilim değerleri hesaplanır ve kaydedilir.
3. 1. ve 2. Adımdaki işlemler her bir kaynak için teker teker yapılır.
4. Tüm kaynaklar için ayrı ayrı bulunan akım veya gerilim değerleri yönleri de dikkate
alınarak toplanır ve tam çözüme ulaşılır.
*Metni yazın+
Deney No: 5
Deneyin Adı:Güç Sakınımı Ve Maksimum Güç Transferi
1.Deneyin Amacı
*Devrede üretilen ve tüketilen güç toplamlarının sıfıra eşit olduğunu deneysel olarak ispat
etmek.
*Yüke maksimum güç aktarmak için yük empedansının hangi koşulları sağlaması gerektiğini
belirlemek.
*Maksimum güç transferi olduğu zaman, devrenin verimini gözlemlemek.
2-Önbilgi
2.1 Güç ve Güç Sakınımı
Bir elektrik devresindeki güç kaynağının amacı, yüke elektrik enerjisi sağlamaktır. Yük bu
enerjiyi, gerekli bazı işleri yapmak için kullanır. Elektrikte iş, elektrik akımının hareketi ile
yapılır. Güç, iş yapma oranıdır. Güç ölçü birimi Watt (W)'tır. Bir amperlik akım üreten bir
voltluk kuvvet, bir wattlık güce karşılık gelir. Wattmetre, güç ölçmek için kullanılan temel
cihazdır. Bir dc devredeki elektriksel güç aşağıdaki üç formülle ifade edilebilir:
P = E × I , P = I2 × R , P = E2 / R
Burada P = güç (watt)
E = gerilim (volt)
I = akım (amper)
R = direnç (ohm)
Güç kaynağı tarafından sağlanan elektriksel gücün, daima devrede harcanan güce
eşittir.(Tellegen Teoremi).
ΣPüretilen=ΣPtüketilen
Güç sakınımı: Σ p = 0
İşaret Referansı: Kaynağın güç harcadığını ya da güç verdiğini tespit etmek amacıyla
kullanırız.
*Metni yazın+
Şekil 1:İşaret Referansı
2.2 Maksimum Güç Transferi
Maksimum güç transferi kuramı; doğrusal bir devrede, yük direnci Thevenin eşdeğer
direncine eşitken, yükün güç kaynağından maksimum gücü çekebileceğini anlatır.
I = Eth / ( Rth + RL )
PRL = I2 × RL
PRL = [ Eth / ( Rth + RL ) ]2 × RL
Veya
PRL = ( Eth2 × RL ) / ( Rth + RL )2
PRL=Eth2/4
Şekil 2:Thevenin eşdeğer devresi
Thevenin eşdeğeri yerine Norton eşdeğeri kullanılması durumunda ise yine aynı sonuçlar
elde edilir. Bu kez, RL üzerine aktarılan maksimum güç Norton eşdeğer kaynağı IN türünden
elde edilir:
PRL=IN2xRth/4
*Metni yazın+
Deney No: 6
Deneyin Adı:Doğru Akım Devrelerinde Geçici Durumların İncelenmesi
1-Deneyin Amacı
*Zamanla değişmeyen DC gerilimlerle beslenen ve RC ve RL devre elemanlarını
birlikte içeren bir elektrik devresinde oluşabilecek geçici olayları incelemek.
*Geçici olaylara neden olan etkenleri ve etkilerini gözlemlemek.
2-Önbilgi
2.1 RC Devresinde Geçici Durum: Sistemlerin bir sürekli durumdan ikinci bir
sürekli duruma geçerken gösterdikleri davranışlara geçici olaylar adı verilir.Şekil
7,1 de verilen seri RC devresinde , s anahtarı açıkken c sığası tümüyle
yüksüzdür.t=0 anında s anahtarı kapatıldığında devrede belirtilen yönde ve
zamanla değişen bir i(t) akımı akmaya başlar.
Şekil-1:Seri bağlı RC devresinde geçici durum
Devreye Kirchoff gerilim yasası uygulanırsa aşağıdaki eşitlik elde edilir:
1∕C x ∫ i(t) dt + Ri(t) = E
Buradan akım ifadesi bulunmak istenirse:
İ(t)=E/R e –t/RC elde edilir.
*Metni yazın+
Akım eşitliğinden yararlanılarak direnç ve sığaç üzerindeki gerilim bağıntıları
aşağıdaki biçimde yazılabilir.
VR(t)=1/C ∫ i(t) dt=E x (1- e –t/RC)
İ(t), VR(t) ve VC(t)’nin zamanla değişimleri,sırasıyla Şekil-2(a),Şekil-2(b)’de
sunulmuştur.
Şekil-2: İ(t), VR(t) ve VC(t)’nin zamanla değişimleri
Bulunan eşitlikler yardımıyla direnç ve sığaç için güç bağıntıları:
PR(t)=VR(t) x i(t) = E2/R x e -2t/RC
PC (t)=VC(t) x i(t)= E2/R x (e-t/RC- e -2t/RC)
Güç bağıntılarının zamana bağlı olan değişim biçimleri Şekil-3’te sunulmuştur.
*Metni yazın+
Şekil-3:RC devresinde direnç ve sığaç güçlerinin zamanla değişimi
2.2 RL Devresinde Geçici Durum Analizi:Eşdeğer devresi Şekil-4’te verilen seri
bir RL devresinde S anahtarı kapatıldığı anda sabit bir gerilim uygulanmaktadır.
Şekil-4:Seri bağı RL devresinde geçici durum
Bu devreye Kirchoff gerilim yasası uygulanırsa aşağıdaki eşitlik elde edilir;
R x i(t)+L di(t)/dt =E
Bu eşitlik çözümlendiğinde akımın zamanla değişimi;
İ(t)=E/R x (1-e-Rt/L)
Olarak bulunur.Akım bağıntısından yararlanılarak direnç ve indüktans
gerilimlerinin zamanla değişimleri hesaplanabilir.
VR(t)=R x i(t)=E x (1-e-Rt/L)
VL(t)=L x di(t) / dt=E x e-Rt/L
İ(t), VR(t), VL(t)’nin zamanla değişimleri, sırasıyla şekil-5(a),Şekil-5(b)’de
sunulmuştur.
*Metni yazın+
Şekil-5: İ(t), VR(t), VL(t)’nin zamanla değişimleri
Direnç ve indüktansa ilişkin güçlerin zamanla değişimleri;
PR(t)= E2/R x (1- 2e -Rt/L+ e -2Rt/L)
PL(t)= E2/R x (e-Rt/L - e -2Rt/L)
Biçiminde bulunur.Bu iki güç bağıntısında toplam gücün zamanla değişimi elde
edilir.
PTop(t) = PL(t)+PR(t) = E2/R x (1- e-Rt/L)
Güç bağıntılarının zamanla değişimleri Şekil-6’da sunulmuştur.
Şekil-6:RL devresinde direnç ve indüktans güçlerinin zamanla değişimi
*Metni yazın+