ELE 201L – Deney 3
İsim: __________________________
Şube: ________
ELE 201L
DEVRE ANALİZİ LABORATUVARI
Süperpozisyon İlkesi ve Thevenin Eşdeğer Devreleri
Deney 3
İMZA KAĞIDI
(Bu sayfa laboratuvarın sonunda asistanlara teslim edilmelidir)
Ön-Çalışma Lab Saatin Başında Teslim Edildi
_______________________
Sözlü Sınav Notu:
_______________________
Deney A Tamamlandı
_______________________
Deney B Tamamlandı
_______________________
Deney C Tamamlandı
_______________________
ELE 201L – Deney 3
İsim: __________________________
Şube: ________
Deneyler
A. Thevenin ve Norton Eşdeğer Devreleri
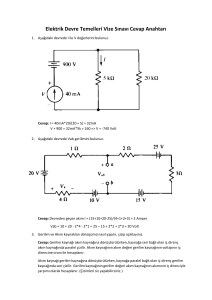
Devre tahtanız üzerinde Şekil 1’de gösterilen devreyi kurunuz. Devrenizde 𝑅1 = 2.2 𝑘Ω, 𝑅2 = 3.3 𝑘Ω,
ve 𝑅3 = 2.2 𝑘Ω direnç değerleri kullanınız. Önce multimetreyi kullanarak devrenin açık devre gerilimini
ölçünüz ve aşağıda verilen tabloda kaydediniz.
Ölçümünüzü ön çalışmadaki hesaplarınızla
karşılaştırınız, farkı yüzde olarak bulunuz. Kısa devre akımı ölçmek için multimetreyi çıkış terminallere
bağlayayınız – bu durumda, multimetre kısa devre olarak işlemektedir. Akım ölçümünüzü tabloya
kaydediniz.
Thevenin direnci ölçmek için üç farklı yöntem uygulanabilir:
1. Kısa devre akımı yöntemi: Açık devre gerilimin ve kısa devre akımın oranı olarak Thevenin direnci
hesaplanabilir.
2. Ohm metre yöntemi: Eğer devre sadece bağımsız kaynaklar içeriyorsa, yani hiç bir bağımlı kaynak
yoksa, multimetreyle çıkış direnci ölçerek Thevenin direnci hesaplanabilir.
Bu ölçümü
gerçekleştirirken bütün bağımsız kaynakları devreden çıkartıp, gerilim kaynakların yerine kısa
devre bağlanmalıdır. Not: Bu yöntem bilinmeyen devreler üzerinde genelde uygulanmaz çünkü
devre aktif veya doğrusal olmayan ögeler içerirse multimetre ölçümü doğru olmaz.
3. Gerilim bölücü yöntemi: Çıkış terminallere potensiyometre bağlayınız. Potensiyometre değerini
çıkış gerilimini açık devre gerilimin yarısı olacağı şekilde ayarlayınız: vout = voc/2 = VTH/2. Şekil 8’in
gösterdiği gerilim bölücü devrede olduğu gibi potensiyometre değeri Thevenin direncine eşit
olduğunda çıkış gerilim kaynak gerilimin (Vs=VTH) yarısına düşmektedir.
Şimdi hesapladığınız Thevenin eşdeğer direnci devre tahtanizda kurunuz ve aynı hesapları
tekrarlayınız.
Ölçümlerinizi tabloda kaydediniz.
Ön çalışmada yaptığınız analitik hesaplar
ölçümlerinize ne kadar uymaktadır? Farklara neler sebep olabilir?
Şekil 8: Thevenin Direncini Hesaplamak İçin Potansiyometre Kullanan Devre
ELE 201L – Deney 3
İsim: __________________________
Şube: ________
Thevenin Eşdeğer Devre Ölçümleri
Ölçüm
Analitik Hesap
Fark
Orijinal Devre
Açık Devre Gerilim
%
Kısa Devre Akım
%
Thevenin Direnç (Yöntem 1)
%
Thevenin Direnç (Yöntem 2)
%
Thevenin Direnç (Yöntem 3)
%
Thevenin Eşdeğer Devre
Açık Devre Gerilim
%
Kısa Devre Akım
%
Thevenin Direnç
%
B. Maksimum Güç Transferi
Şekil 2’de olduğu gibi Deney A’de kurulan devreye 10 k’luk potensiyometre bağlayınız.
Potensiyometreyi çıkış gerilimi V0 = 0.1 VTH olacağı şekilde ayarlayınız. Potensiyometreyi devreden
ayırarak multimetreyle direncini ölçünüz ve potensiyometrenin devreye bağlıyken tükettiği gücü
hesaplayınız. Ölçümlerinizi tabloya kaydediniz. Aynı prosedürü V0 = 0.2 VTH, 0.3 VTH, 0.4 VTH, 0.5 VTH,
0.6 VTH, 0.7 VTH, 0.8 VTH, ve 0.9 VTH için tekrarlayınız. Hesaplanan güç hangi direnç değeri için en
büyükyür? Güç transferin maksimum olduğu yük direncin değeri ön çalışma da yapılan hesaplarla
uyumlu mu?
Maksimum Güç Transferi için hesaplanan yük direnç değeri:
V0
0.1 VTH
0.2 VTH
0.3 VTH
0.4 VTH
0.5 VTH
0.6 VTH
0.7 VTH
0.8 VTH
0.9 VTH
Potensiyometre Direnci
Tüketilen Güç
ELE 201L – Deney 3
İsim: __________________________
Şube: ________
Yük Doğrusu Analizi
Yük doğrusu analizi devrelerin – özellikle doğrusal olmayan devrelerin – grafik çözümünde çok
kullanılan bir yöntemdir. Diyelim ki bir devreye yük direnci bağlandı, Şekil 9’da gösterildiği gibi. Grafik
yük analizi için önce devrenin v-i ilişkisi çizdirilmektedir. Eğer devre doğrusal değil ise, v-i ilişkisinin
eğrisi de doğrusal olmayacaktır. Ancak, tüm doğrusal devrelerin de Thevenin eşdeğeri bulunduğundan,
bu deney’de ele alacağımız doğrusal devrelerin v-i ilişkisini Şekil 10’de gösterildiği gibi çizdirebiliriz.
Bağlanan yükü v-i ilişkisini aynı eksenler üzerinde çizersek, bu iki eğrinin kesiştiği nokta bağlantığı
zaman terminallerin gerilim ve akım değerini vermektedir.
Şekil 9: Genel Bir Devreye Bağlanan Yük Direnci
Şekil 10: Doğrusal Bir Devrenin Yük Doğrusu Analizi
ELE 201L – Deney 3
İsim: __________________________
Şube: ________
Grafiksel yük doğrusu analizi yöntemiyle, maksimum güç transferini sağlayan RL direnç değeri için
yüke verilen akımı hesaplayınız. Analizi aşağıda verilen eksenler üzerinde yapınız.
iL =
ELE 201L – Deney 3
İsim: __________________________
Şube: ________
C. Süperpozisyon İlkesi
Şekil 7’de gösterilen devreyi aşağıda verilen öge değerleri için devre tahtanıza kurunuz.
R1 = 16 k
R3 = 3.9 k
R5 = 1.1 k
R2 = 16 k
R4 = 1.1 k
R6 = 8.2 k
Va = 12 V
Vb = 5 V
1. Önce tüm gerilim kaynaklar bağlıyken açık devre gerilimini ve Thevenin eşdeğer direnci
ölçünüz. Thevenin direnci ölçmek için istediğiniz yöntemi kullanabilirsiniz, yalnız hangi yöntemi
kullandığınızı not ederen laboratuvar raporunuzda belirtiniz.
2. Şimdi Va kaynağı devreden çıkartın ve yerine bir kısa devre bağlayınız. Açık devre gerilim ve
Thevenin direnç ölçümlerinizi tekrarlayınız.
3. Va kaynağı tekrar devreye bağlayarak, bu kez Vb kaynağı devreden çıkartınız ve yerine bir
kısa devre bağlayınız. Açık devre gerilim ve Thevenin direnç ölçümlerinizi tekrarlayınız.
Tüm ölçümlerinizi aşağıda verilen tabloda kaydediniz. Ölçümlerinize bakarak, yorumlayınız –
süperpozisyon ilkesiyle ölçülen Thevenin eşdeğer devre, tüm kaynaklar bağlıyken ölçülen
Thevenin eşdeğer devreyle aynı mı? Ölçerek bulduğunuz Thevenin eşdeğer devreleri önçalışmada yaptığınız analitiz hesaplarla uyumlu mudur? Değilse sebepleri açıklayınız.
Süperpozisyon Deney Ölçümleri
Ölçüm
Analitik Hesap
Fark
Orijinal Devre
Açık Devre Gerilim
%
Thevenin Direnç
%
Sadece Va Bağlıyken
Açık Devre Gerilim
%
Thevenin Direnç
%
Sadece Vb Bağlıyken
Açık Devre Gerilim
%
Thevenin Direnç
%