üçgende kenarortay
açıortay ve Kazanım
yüksekl
İk
:Üçgende kenarortay, açıortay ve yüksekliği inşa eder.
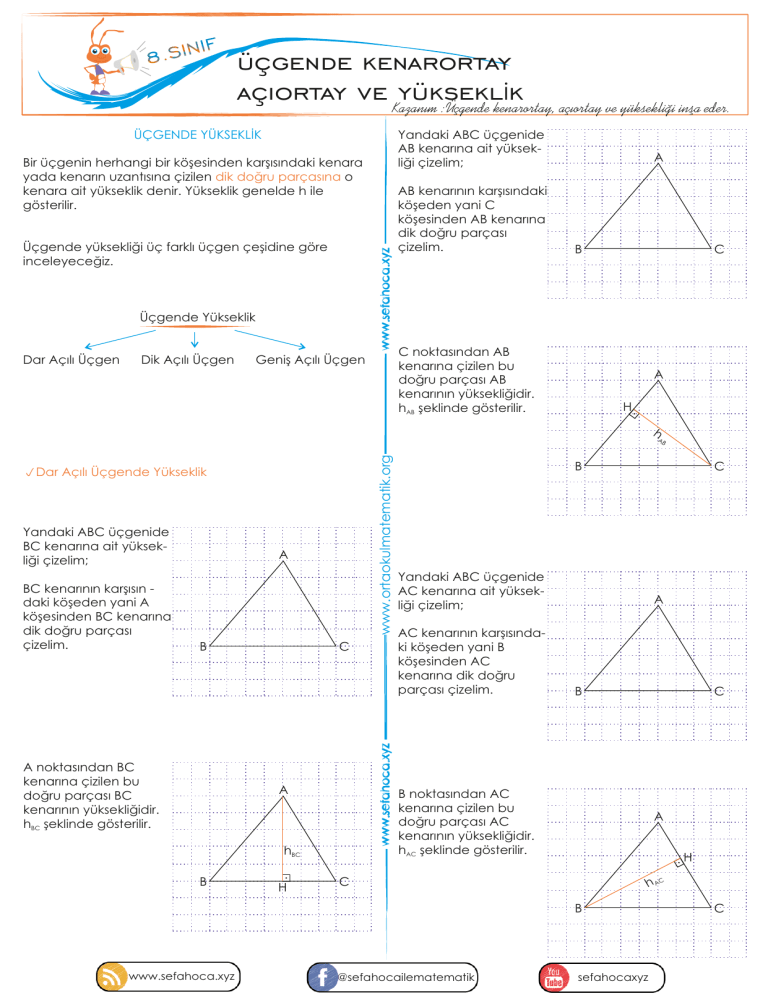
ÜÇGENDE YÜKSEKLİK
Yandaki ABC üçgenide
AB kenarına ait yüksekliği çizelim;
Bir üçgenin herhangi bir köşesinden karşısındaki kenara
yada kenarın uzantısına çizilen dik doğru parçasına o
kenara ait yükseklik denir. Yükseklik genelde h ile
gösterilir.
AB kenarının karşısındaki
köşeden yani C
köşesinden AB kenarına
dik doğru parçası
çizelim.
Üçgende yüksekliği üç farklı üçgen çeşidine göre
inceleyeceğiz.
A
B
C
Üçgende Yükseklik
Dar Açılı Üçgen
Dik Açılı Üçgen
C noktasından AB
kenarına çizilen bu
doğru parçası AB
kenarının yüksekliğidir.
hAB şeklinde gösterilir.
Geniş Açılı Üçgen
A
H
h
www.ortaokulmatematik.org
AB
Dar Açılı Üçgende Yükseklik
Yandaki ABC üçgenide
BC kenarına ait yüksekliği çizelim;
BC kenarının karşısın daki köşeden yani A
köşesinden BC kenarına
dik doğru parçası
çizelim.
A
B
A noktasından BC
kenarına çizilen bu
doğru parçası BC
kenarının yüksekliğidir.
hBC şeklinde gösterilir.
C
A
H
C
Yandaki ABC üçgenide
AC kenarına ait yüksekliği çizelim;
AC kenarının karşısındaki köşeden yani B
köşesinden AC
kenarına dik doğru
parçası çizelim.
A
B
C
B noktasından AC
kenarına çizilen bu
doğru parçası AC
kenarının yüksekliğidir.
hAC şeklinde gösterilir.
hBC
B
B
A
H
C
h AC
B
www.sefahoca.xyz
@sefahocailematematik
sefahocaxyz
C
Dik Açılı Üçgende Yükseklik
Yandaki ABC üçgenide
AC kenarına ait yüksekliği çizelim;
Yandaki ABC üçgenide
AB kenarına ait yüksekliği çizelim;
AB kenarının karşısındaki
köşeden yani C
köşesinden AB kenarına
dik doğru parçası
çizelim.
A
AC kenarının
karşısındaki köşeden
yani B köşesinden AC
kenarına dik doğru
parçası çizelim.
B
B
B noktasından AC
kenarına çizilen bu
doğru parçası AC
kenarının yüksekliğidir.
hBC şeklinde gösterilir.
A
C
C
C noktasından AB
kenarına çizilen bu
doğru parçası AB
kenarının yüksekliğidir.
Bu yükseklik aynı
zamanda üçgenin dik
kenarlarından bir
tanesidir.
hAB şeklinde gösterilir.
A
A
H
B
hAB
B
Yandaki ABC üçgenide
BC kenarına ait yüksekliği çizelim;
C
A
BC kenarının
karşısındaki köşeden
yani A köşesinden BC
kenarına dik doğru
parçası çizelim.
B
A noktasından BC
kenarına çizilen bu
doğru parçası BC
kenarının yüksekliğidir.
Bu yükseklik aynı
zamanda üçgenin dik
kenarlarından bir
tanesidir.
hBC şeklinde gösterilir.
www.ortaokulmatematik.org
h AC
Geniş Açılı Üçgende Yükseklik
Yandaki ABC üçgenide
AC kenarına ait yüksekliği çizelim;
A
AC kenarının
karşısındaki köşeden
yani B köşesinden AC
kenarına dik doğru
parçası çizelim.
B
C
B noktasından AC
kenarına çizilen bu
doğru parçası AC
kenarının yüksekliğidir.
hAC şeklinde gösterilir.
A
C
C
A
hBC
hAC
B
www.sefahoca.xyz
C
@sefahocailematematik
web sitemizi
ziyaret etmeyi unutmayın...
B
sefahocaxyz
C
Yandaki ABC üçgenide
BC kenarına ait yüksekliği çizelim;
A
Bir üçgende üç adet yükseklik vardır.
BC kenarının
karşısındaki köşeden
yani A köşesinden BC
kenarına dik doğru
parçası çizmeye
çalıştığımızda çizilen
doğru parçalarının dik
olmadığını görürüz.Bu
nedenle kenarın
uzantısına dik doğru
parçası çizeriz.
A noktasından BC
kenarının uzantısına
çizilen bu doğru parçası
BC kenarının
yüksekliğidir.
hBC şeklinde gösterilir.
Dar açılı üçgende yüksekliklerin üçü de üçgenin
içindedir.
B
Dik açılı üçgende yüksekliklerden biri üçgenin
içinde, ikisi kenarlar üzerindedir.
C
Geniş açılı üçgende yüksekliklerden biri üçgenin
içinde, ikisi üçgenin dışındadır.
örnek:
A
A
Yandaki ABC
üçgeninde BC
kenarı üzerindeki
hangi nokta ile A
köşesi birleştirilirse
BC kenarına ait
yükseklik elde
edilir?
hBC
Yandaki ABC üçgenide
AB kenarına ait yüksekliği çizelim;
C
A
AB kenarının karşısındaki
köşeden yani C
köşesinden AB kenarına
dik doğru parçası
çizmeye çalıştığımızda
çizilen doğru
parçalarının dik
olmadığını görürüz.Bu
nedenle kenarın
uzantısına dik doğru
parçası çizeriz.
C noktasından AB
kenarının uzantısına
çizilen bu doğru parçası
AB kenarının
yüksekliğidir.
hAB şeklinde gösterilir.
B
www.ortaokulmatematik.org
Bc’nin uzantısı
B
C
B
C
S E F A
örnek:
A
A
B
C
n
’ni
Ab
B
C
Yandaki ABC
üçgeninde BC
kenarına ait
yüksekliğin
uzunluğu ile BC
kenarının uzunluğu
farkı kaç birimdir?
uza
hAB
sı
ntı
www.sefahoca.xyz
@sefahocailematematik
web sitemizi
ziyaret etmeyi unutmayın...
sefahocaxyz
Üçgenin bir köşesinden karşı kenarına çizilen doğru
parçası o kenarı iki eş parçaya bölmüş ise;
başka bir ifadeyle köşeden çizilen doğru parçası kenarın
orta noktasına gelmiş ise bu doğru parçası
kenarortaydır.
İkizkenar üçgende eş olan kenarlara ait
yüksekliklerin uzunlukları birbirine eşittir.
Eşkenar üçgenin tüm yüksekliklerinin uzunluğu
birbirine eşittir.
S
A
K
VEA
E
L
C
ABC ikizkenar üçgeninde
AB = AC ise hAB = hAC dir.
hBC üçgeni iki eş parçaya
ayırır.
KLM eşkenar üçgeninde
tüm yüksekliklerin uzunluğu
birbirine eşittir.
ÜÇGENDE KENARORTAY
Bir üçgenin herhangi bir kenarının orta noktası ile
karşısındaki köşeyi birleştiren doğru parçasına
kenarortay denir. Kenarortay genelde V ile gösterilir.
A
Yukarıdaki SEA üçgeninin S köşesinden EA kenarına
çizilen doğru parçası EA kenarını iki eş parçaya
ayırmıştır.EA kenarının orta noktası F olduğuna göre orta
nokta ile karşı köşesi birleştiren SF doğru parçası EA
kenarının kenarortayıdır.
örnek:
A
B
X
B
Z
Y
I
C
II III IV
Yandaki ABC
üçgeninde BC
kenarı üzerindeki
noktalardan
hangisi A köşesi ile
birleştirildiğinde
üçgene ait bir
kenarortay elde
edilir?
C
Yukarıdaki ABC üçgeninde X,Y,Z noktaları üzerinde
bulundukları kenarların orta noktalarıdır.
örnek:
A
BC kenarının orta noktası (Y) ile karşısındaki köşeyi (A
köşesini) birleştiren doğru parçasında BC kenarının
kenarortayı denir. VBC şeklinde ifade edilir.
I
AB kenarının orta noktası (X) ile karşısındaki köşeyi (C
köşesini) birleştiren doğru parçasında AB kenarının
kenarortayı denir. VAB şeklinde ifade edilir.
AC kenarının orta noktası (Z) ile karşısındaki köşeyi (B
köşesini) birleştiren doğru parçasında AC kenarının
kenarortayı denir. VAC şeklinde ifade edilir.
www.sefahoca.xyz
A
F
M
www.ortaokulmatematik.org
B
III II
IV
B
@sefahocailematematik
web sitemizi
ziyaret etmeyi unutmayın...
Yandaki ABC
üçgeninde BC
kenarına ait
kenarortay, üçgen
içinde verilen
noktalardan
hangisinin
üzerinden geçer?
C
sefahocaxyz
Kenarortaylar üçgenin içinde bir noktada
kesişirler. Kenarortayların kesiştiği bu nokta
üçgenin ağırlık merkezidir.
Açıortay, kenarın ortasından geçmek
zorunda değildir.
Açıortay, kenara dik olarak çizilmek zorunda
değildir.
Açıortay sadece bulunduğu açıyı iki eş açıya
ayırmak zorundadır.
ÜÇGENDE AÇIORTAY
Bir üçgende bir iç açıyı iki eş parçaya ayıran ve açının
bulunduğu köşeyi karşısındaki kenarla birleştiren doğru
parçasına o açının açıortayı denir. Açıortay genelde n
ile gösterilir.
örnek:
A
0
40 0 40
Yandaki ABC üçgeninde A
açısına ait açıortayı
çizelim;
A
800'lik A açısını 400'lik iki eş
açıya bölen bir doğru
parçası çiziyoruz.
600
400
A
800
C
nA, açıortaydır.
Yandaki ABC üçgeninde B
açısına ait açıortayı
çizelim;
600'lik B açısını 300'lik iki eş
açıya bölen bir doğru
parçası çiziyoruz.
30
30 0
0
B
400
0
600
B
350
C
örnek:
A
nB, açıortaydır.
Yandaki ABC üçgeninde C
açısına ait açıortayı
çizelim;
A
80
C
www.ortaokulmatematik.org
B
D
Yandaki ABC
üçgeninde [CD],
ACB’nin
açıortayıdır.
m(ABC) = 600
m(BCD) = 250
olduğuna göre
m(BAC) = ?
Yandaki ABC dik
üçgeninde [AD]
açıortaydır.
m(ACB) = 400 ise
m(BAD) = ?
B
400
D
C
400'lik C açısını 200'lik iki eş
açıya bölen bir doğru
parçası çiziyoruz.
0
B
60
0
200
20
C
www.sefahoca.xyz
nC, açıortaydır.
@sefahocailematematik
web sitemizi
ziyaret etmeyi unutmayın...
sefahocaxyz
ÜÇGENDE KENAR ORTA DİKME
Üçgenin herhangi bir kenarının orta noktasından geçen
ve kenara dik olan doğru parçasına kenar orta dikme
denir.
Bir üçgende yükseklik, kenarortay ve
açıortay uzunlukları ;
Kenar orta dikme, üçgenin köşesinden geçmek zorunda
değildir.
yükseklik < açıortay < kenarortay
şeklinde sıralanabilir.
Kenar orta dikme, kenarın ortasından geçmek
zorundadır.
Kenar orta dikme, kenara dik olmak zorundadır.
A
ÜÇGENDE YÜKSEKLİK, KENARORTAY, AÇIORTAY İLE İLGİLİ
ÇIKMIŞ TEOG SORULARI
2013-2014
TEOG-2
ABC üçgeninin BC
kenarına ait kenar orta
dikmesini çizelim;
BC kenarının orta
noktasını buluyoruz. Bu
noktadan geçen ve
kenara dik olan bir
doğru parçası çiziyoruz.
A
ABC üçgeninin AB
kenarına ait kenar orta
dikmesini çizelim;
AB kenarının orta
noktasını buluyoruz. Bu
noktadan geçen ve
kenara dik olan bir
doğru parçası çiziyoruz.
www.ortaokulmatematik.org
C
B
C
B
2014-2015
TEOG-2
A
ABC üçgeninin AC
kenarına ait kenar orta
dikmesini çizelim;
AC kenarının orta
noktasını buluyoruz. Bu
noktadan geçen ve
kenara dik olan bir
doğru parçası çiziyoruz.
C
B
www.sefahoca.xyz
@sefahocailematematik
web sitemizi
ziyaret etmeyi unutmayın...
sefahocaxyz
www.ortaokulmatematik.org
2015-2016
TEOG-2
2015-2016
TEOG-2 MZRT
www.sefahoca.xyz
@sefahocailematematik
web sitemizi
ziyaret etmeyi unutmayın...
sefahocaxyz