Mekanik
Kuvvetlerin etkisi altında cisimlerin denge ve hareket
şartlarını anlatan ve inceleyen bir bilim dalıdır. Amacı
fiziksel olayları açıklamak, önceden tahmin etmek ve
böylece mühendislik uygulamalarına ışık tutmaktır.
Mekanik fiziksel olayları incelediği için fiziksel
bilimlerdendir. Bununla birlikte matematiğe ve
mühendislik konularına bağlanabilir.
Mühendislik
Matematik
Mekaniğin Alt Dalları
• Şekil Değiştirmeyen Cisimler Mekaniği (Rijit Cisimler
Mekaniği)
a. Statik : duran cisimleri inceler
b. Dinamik :hareketli cisimleri inceler
b.a.
Kinematik
:hareketin
sebeplerini
hesaba
katmaksızın (yer değ.,hız, ivme, zaman)
b.b. Kinetik : hareketin sebepleri ile kendisi arasında ilişki
• Şekil Değiştirebilen Cisimler Mekaniği (Mukavemet)
• Akışkanlar Mekaniği
a. Sıkıştırılamayan Akışkanlar Mekaniği (Sıvılar)
b. Sıkıştırılabilen Akışkanlar Mekaniği (Gazlar)
Geçmişi çok eski çağlara dayanan statiğin, bilimsel temellere
dayandırılışı yeni sayılabilir. Örneğin, Paralel Kenar İlkesi SIMON
STEVINUS (1548-1620) tarafından önerilmiştir.
Paralelkenar Kanunu: Bir maddesel noktaya etkiyen iki kuvvetin
yerine bir tek kuvvet koymak mümkündür; bileşke adı verilen bu
kuvvet, kenarları verilen kuvvetlere eşit bir paralelkenarın köşegenini
çizerek elde edilir.
Dinamiğin geçmişi, statikten de daha yenidir. İlk bilimsel
çalışmalar GALILEO GALILEI (1564-1642) ile başlamakla
birlikte, günümüze kadar uzanan temelleri ISAAC NEWTON
(1642-1726) atmıştır.
Mukavemet konusunda ilk metodlu çalışma Rönesans
zamanında LEONARDO DA VINCI (1452-1519) ile başlar.
Kuvvet : Bir cismin diğerine etkisini gösterir. Kuvvet şu elemanlarla belirlenir. Şiddet, tatbik noktası, yön ve doğrultu. Yön ve doğrultu vektör olduklarından kuvvet de bir vektörel büyüklük olarak tanımlanır.
B
A
y
B
Fyy
Fy
O
z
Fz
F
F
O
A
D
x
E
Fx
Fz
x
y
E
C
z
B
C
Fy F
O
z
A
Fx
E
z
Fz
Fx
C
D
x
D
x
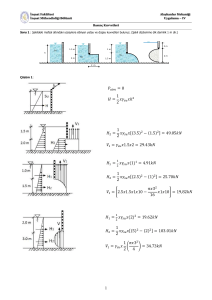
Statik dersi 1. sınıfın 2. yarıyılında okutulmakta olup işlenecek konular aşağıda verilmiştir;
•Düzlemde kuvvetler, yükler
•Düzlemde bağlar, taşıyıcı sistemler
•Üç mafsallı sistemler
•Gerber kirişler, genel mafsallı sistemler
•Kafes sistemler
•Kablolar
•Uzay kuvvetler ve yükler
•Uzayda bağlar
•Ağırlık merkezi
•Sürtünme •Virtüel iş
Yayılı yükler
Mesnetler ve mesnet kuvvetleri
Taşıyıcı sistemler
Kafes sistem
Üç mafsallı sistem
Uzay kuvvetler
Gerber Kiriş
Virtüel
iş
Ağırlık merkezi
Sürtünme
Mukavemet : taşıyıcı sistemlerin hesabı
ile uğraşan uygulamalı bir bilimdir
• Emniyet
• Ekonomi
• Estetik
Maliyet
Optimum
nokta
Emniyet
Mukavemet dersleri içerisinde işlenecek konular;
‐ İç Kuvvetler
‐ Şekil Değiştirme
‐ Gerilme – Şekil değiştirme bağıntıları
‐ Şekil Değiştirme Enerjisi
‐ Mekanik Özellikler
‐ Kırılma Teorileri
‐ Kesit Etkileri
‐ Eksenel Normal Kuvvet
‐ Kesme Kuvveti
‐ Burulma
•Atalet Momenti
•Basit Eğilme
•Kesmeli Eğilme
•Bileşik Kirişler
•Kayma Merkezi
•Elastik Eğri ( Diferansiyel Denklem Yöntemi, Mohr Yöntemi, Konsol Çubuk Yöntemi)
•Üç Moment Denklemi
•Eksantrik Normal Kuvvet
•Burulmalı Eğilme
•Enerji Yöntemi (Virtüel İş Yöntemi, Castigliano Yöntemi)
•Burkulma
gerilme
İç kuvvet ve gerilme
Şekil değiştirme
Eksenel normal kuvvet
Kesme,
Eğilme,
burulma
Kesit etkileri
eğilme
Bileşik çubuklar
Elastik eğri
burkulma
Atalet momenti
Burulmalı eğilme
Enerji yöntemi
ile yerdeğiştirme
Eksantrik normal kuvvet
Dinamik 2. sınıfın 2. yarıyılında okutulan ders olup;
Maddesel Noktaların
‐ Kinematiği, bağıl, bağlı hareket, eğrisel hareket, dik bileşenler, teğetsel ve normal , kutupsal ve silindirik koordinatlarda hız ve ivme bileşenleri
‐ Kinetiği, maddesel noktalar sistemi, merkezsel hareket, enerji yöntemleri, konservatif kuvvetler, İş‐Enerji İlkesi, Enerjinin Korunumu, İmpuls‐Momentum İlkesi, Çarpışma, Açısal Momentum İlkesi, Değişken kütleli sistemler
Rijit Cisimlerin ‐ Kinematiği, ‐ Kinetiği, İş‐Enerji İlkesi, İmpuls‐Momentum İlkesi
Mekanik Titreşimler
gibi konular işlenmektedir.
xC
xA
xB
C
A
B
ay
y
P
az
W
kartezyen
ax
dy
y
y2
A
x
z
A2
enerji
y
y1
an
at
Teğetsel, normal
v
P
x
O
P
Açısal momentum
a
r
O
v0
r
P
ar
x
kutupsal
0
r0
O
P0
hareket
Bağlı hareket
mivi
B
S
A
(m)vA
çarpışma
(m)vB
F t
S
M t
Değişken kütleli sistemler
B
mivi
S
A
Mekanik titreşim
Matematiğin kullanımları
F x
x lim
A0 A
-xm
xy lim
A 0
V yx
A
Vzx
xz lim
A0 A
T dF dA
O
Equilibrium
x
+xm
+
P
d 4v
EI 4 EIv ıv ( z ) q y z
dz
dM x
d 3v
EI 3 EIv ııı ( z ) Ty
dz
dz
d 2v
EI 2 EIv ıı ( z ) M x
dz
dv
EI
EIv ı ( z )
dz
EIv( z ) f