İnşaat Fakültesi
İnşaat Mühendisliği Bölümü
Akışkanlar Mekaniği
Uygulama – IV
Basınç Kuvvetleri
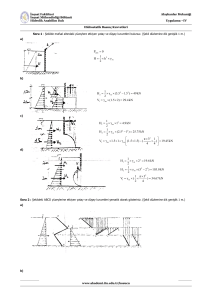
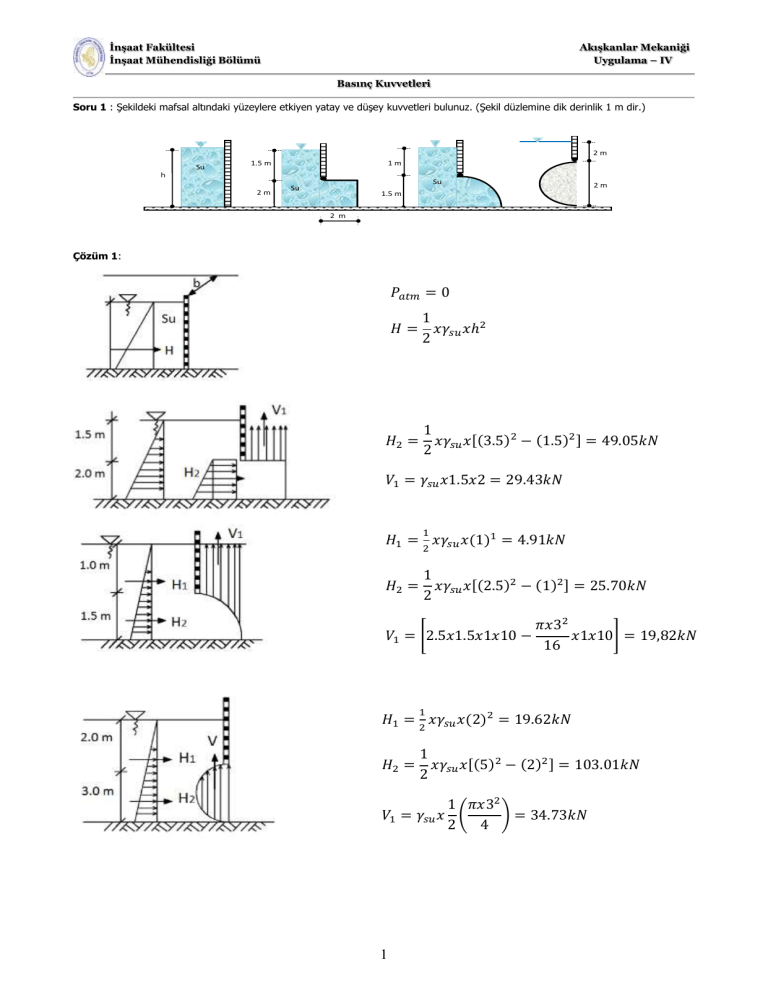
Soru 1 : Şekildeki mafsal altındaki yüzeylere etkiyen yatay ve düşey kuvvetleri bulunuz. (Şekil düzlemine dik derinlik 1 m dir.)
2m
Su
1.5 m
1m
h
2m
Su
Su
2m
1.5 m
2 m
Çözüm 1:
𝑃𝑎𝑡𝑚 = 0
1
𝐻 = 𝑥𝛾𝑠𝑢 𝑥ℎ2
2
1
𝐻2 = 𝑥𝛾𝑠𝑢 𝑥[(3.5)2 − (1.5)2 ] = 49.05𝑘𝑁
2
𝑉1 = 𝛾𝑠𝑢 𝑥1.5𝑥2 = 29.43𝑘𝑁
1
𝐻1 = 2 𝑥𝛾𝑠𝑢 𝑥(1)1 = 4.91𝑘𝑁
1
𝐻2 = 𝑥𝛾𝑠𝑢 𝑥[(2.5)2 − (1)2 ] = 25.70𝑘𝑁
2
𝑉1 = [2.5𝑥1.5𝑥1𝑥10 −
𝜋𝑥32
𝑥1𝑥10] = 19,82𝑘𝑁
16
1
𝐻1 = 2 𝑥𝛾𝑠𝑢 𝑥(2)2 = 19.62𝑘𝑁
1
𝐻2 = 𝑥𝛾𝑠𝑢 𝑥[(5)2 − (2)2 ] = 103.01𝑘𝑁
2
1 𝜋𝑥32
𝑉1 = 𝛾𝑠𝑢 𝑥 (
) = 34.73𝑘𝑁
2
4
1
İnşaat Fakültesi
İnşaat Mühendisliği Bölümü
Akışkanlar Mekaniği
Uygulama – IV
Basınç Kuvvetleri
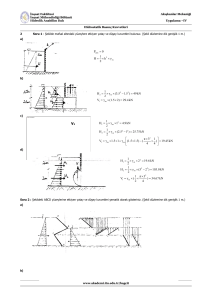
Soru 2 : Şekildeki ABCD yüzeylerine etkiyen yatay ve düşey kuvvetleri şematik olarak gösteriniz. (Şekil düzlemine dik derinlik 1 m dir.)
A
A
Su
C
B
Su
C
Su
A
D
B
Su
BB
A
C
D
Su
Su
E
Çözüm 2:
2
D
İnşaat Fakültesi
İnşaat Mühendisliği Bölümü
Akışkanlar Mekaniği
Uygulama – IV
Basınç Kuvvetleri
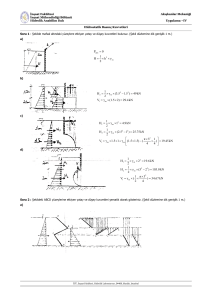
Soru 3 : Şekilde görülen A noktasından mafsallı AB kapağının genişliği 2 m olup bir haznenin iki bölümünü ayıran duvar üzerinde
bulunmaktadır.
a. Bölmelerde su olması durumunda,
b. Bölmelerde yağ olması durumunda, kapağın açılmaması için B noktasına uygulanması gereken kuvvetin yönünü ve şiddetini bulunuz.
(𝛾𝑦𝑎ğ = 7.85𝑘𝑁/𝑚3 )
0.8 m
A
1.2 m
Mafsal
Su
B
Sonuç:
Fsu=12.85 kN,
Su
0.9 m
Fyag=10.28 kN
Çözüm 3:
𝐻1𝑠𝑢 = 9.81𝑥0.8𝑥1.2𝑥2 = 18.83𝑘𝑁
𝐻1𝑦𝑎ğ = 7.85𝑥0.8𝑥1.2𝑥2 = 15.07𝑘𝑁
1
𝑋1.2 = 0.6
2
1
𝐻2𝑠𝑢 = x9.81x1.2x1.2x2 = 14.13kN
2
1
𝐻2𝑦𝑎ğ = 𝑥7.85𝑥1.2𝑥1.2𝑥2 = 11.30𝑘𝑁
2
2
𝑙2 = 𝑥1.2 = 0.8
3
1
𝐻3𝑠𝑢 = x9.81x0.9x0.9x2 = 7.95kN
2
1
𝐻3𝑦𝑎ğ = 𝑥7.85𝑥0.9𝑥0.9𝑥2 = 6.38𝑘𝑁
2
2
𝑙3 = 0.3 + 𝑥0.9 = 0.9
3
𝑙1 =
3
İnşaat Fakültesi
İnşaat Mühendisliği Bölümü
Akışkanlar Mekaniği
Uygulama – IV
Basınç Kuvvetleri
∑ 𝑀𝐴 = 0; 𝑠𝑢 𝑖ç𝑖𝑛
𝐻1𝑠𝑢 𝑥𝑙1 + 𝐻2𝑠𝑢 𝑥𝑙2 − 𝐻3𝑠𝑢 𝑥𝑙3 − 1.2𝑥𝐹 = 0
𝐹𝑠𝑢 = 12.85𝑘𝑁
∑ 𝑀𝐴 = 0; 𝑦𝑎ğ 𝑖ç𝑖𝑛
𝐻1𝑦𝑎ğ 𝑥𝑙1 + 𝐻2𝑦𝑎ğ 𝑥𝑙2 − 𝐻3𝑦𝑎ğ 𝑥𝑙3 − 1.2𝑥𝐹𝑦𝑎ğ = 0
𝐹𝑦𝑎ğ = 10.28𝑘𝑁
Soru 4 : Şekilde görülen A noktasından mafsallı dikdörtgen AB kapağının genişliği 4 m, ağırlığı 392.4 kN’ dur. Kapağın kendiliğinden
açılmaması için memba tarafındaki “h” su derinliği ne olmalıdır. Sonuç: hmax=5.5 m
A
h max
Mafsal
Su
2m
α
B
Çözüm 4:
𝐻1 − 𝐻3 = 𝛾𝑥(ℎ𝑚𝑎𝑥 − 2) − 𝛾𝑥1 = 𝛾𝑥(ℎ𝑚𝑎𝑥 − 3)
𝐻2 − 𝐻4 = 𝛾𝑥ℎ𝑚𝑎𝑥 − 3𝑥𝛾 = 𝛾𝑥(ℎ𝑚𝑎𝑥 − 3)
∑ 𝑀𝐴 = −[𝛾𝑥(ℎ𝑚𝑎𝑥 − 3)𝑥2𝑥4𝑥1] − [𝛾𝑥(ℎ𝑚𝑎𝑥 − 3)𝑥2𝑥4𝑥1] + 392.4𝑥1 = 0
2𝑥(ℎ𝑚𝑎𝑥 − 3) = 5
ℎ𝑚𝑎𝑥 = 5.5𝑚
Soru 5 : Şekildeki dikdörtgen kapak sisteminde;
a-
Kapağa gelen basınç kuvvetini ve tatbik noktasını,
b-
A ve B noktalarındaki reaksiyon kuvvetini bulunuz.
Not: Kapağın şekil düzlemine dik genişlik 5 m dir. A noktasındaki temas yüzeyi cilalıdır.
Sonuç:
b-
a) Fsu=5886 kN,
HA=4495.92 kN
B noktasından tatbik noktası,
HB=-212.88 kN,
4.58 m
VB=3531.60 kN
4
İnşaat Fakültesi
İnşaat Mühendisliği Bölümü
Akışkanlar Mekaniği
Uygulama – IV
Basınç Kuvvetleri
Su
A
15 m
6m
B
Mafsal
8m
Çözüm 5:
𝑉1 = 𝛾𝑠𝑢 𝑥9𝑥8𝑥5 = 3531.60𝑘𝑁
𝑉2 =
1
𝑥𝛾 𝑥8𝑥6𝑥5 = 1177.20𝑘𝑁
2 𝑠𝑢
𝐻1 = 𝛾𝑠𝑢 𝑥6𝑥9𝑥5 = 2648.70𝑘𝑁
1
𝐻2 = 𝑥𝛾𝑠𝑢 𝑥6𝑥5𝑥(15 − 9) = 882.90𝑘𝑁
2
Her bir kuvvetin B noktasına uzaklığı; (yatay, düşey)
8
𝑙𝑣1 = 4𝑚, 𝑙𝑣2 = 𝑚,
3
𝑙𝐻1 = 3𝑚, 𝑙𝐻2 = 2𝑚
Bileşke kuvvet;
2
𝐹 = √(∑ 𝐻İ ) + (∑ 𝑉İ )
2
→ 𝐹 = √(3531.60 + 1177.20)2 + (2648.70 + 882.90)2
𝐹 = 5886𝑘𝑁
8
𝐹𝑥𝑦𝑚 = 3531.60𝑥4 + 1177.20𝑥 + 2648.70𝑥3 + 882.90𝑥2
3
26977.50
𝑦𝑚 =
= 4.58𝑚 (𝐾𝑎𝑝𝑎𝑘 𝑏𝑜𝑦𝑢𝑛𝑐𝑎 𝐵 𝑛𝑜𝑘𝑡𝑎𝑠𝚤𝑛𝑑𝑎𝑛 𝑢𝑧𝑎𝑘𝑙𝚤𝑘)
5886
5
İnşaat Fakültesi
İnşaat Mühendisliği Bölümü
Akışkanlar Mekaniği
Uygulama – IV
Basınç Kuvvetleri
A noktasındaki P reaksiyon kuvveti,
∑ 𝑀𝐵 = 0;
−𝐹𝑥𝑦𝑚 + 𝑝𝑥6 = 0
𝑃=
𝐹𝑥𝑦𝑚 5886𝑥4.58
=
= 4492.98𝑘𝑁
6
6
∑ 𝑋 = 0 → −𝑃 + 𝐻𝐵 + 𝐹𝑠𝑖𝑛𝛼 = 0 → −4492.98 + 𝐻𝐵 + 5886𝑋
∑ 𝑌 = 0 → 𝑉𝐵 = 𝐹𝑐𝑜𝑠𝛼 → 𝑉𝐵 = 5886𝑥
6
= 0 → 𝐻𝐵 = 961.38𝑘𝑁
10
8
→ 𝑉𝐵 = 4708.80𝑘𝑁
10
Soru 6 : Şekildeki silindir kapağın, düzlemine dik derinliği’ 1 m alarak, kapağa gelen hidrostatik basınç kuvvetinin yatay ve düşey
bileşenlerini, bileşke kuvvetin değerini ve A noktasına göre tatbik noktasının koordinatlarını bulunuz. (𝛾𝑦𝑎ğ = 7.85𝑘𝑁/𝑚3 )
A
6m
Yağ B
D
C
Sonuç:
R= 204.83 kN (Bileşke kuvvet)
Çözüm 6:
1
𝐻1 = 𝑥𝛾𝑦𝑎ğ 𝑥62 𝑥1 = 141.26𝑘𝑁
2
1 𝜋𝑥62
𝑉1 = 𝑥
𝑥7.85𝑥1 = 110.98𝑘𝑁
2
4
1
𝐻2 = 𝑥9.81𝑥32 𝑥1 = 44.15𝑘𝑁
2
𝑉2 =
1 𝜋𝑥62
𝑥
𝑥9.81𝑥1 = 69.36𝑘𝑁
4
4
∑ 𝐻 = 141.26 − 44.15 = 97.11𝑘𝑁
6
Su
3m
İnşaat Fakültesi
İnşaat Mühendisliği Bölümü
Akışkanlar Mekaniği
Uygulama – IV
Basınç Kuvvetleri
∑ 𝑉 = 110.98 + 69.36 = 180.34𝑘𝑁
Kapak silindirik olduğuna göre bileşke kuvvet dairenin merkezinden geçecektir.
180.34 kN
97.11 kN
𝑡𝑎𝑛𝜃 =
180.34
= 1.85 → 𝜃 = 61.69°
97.11
𝑥𝐴 = 3𝑥𝑐𝑜𝑠𝜃 = 1.423𝑚
𝑦𝐴 = 3 − 3𝑥𝑠𝑖𝑛𝜃 = 0.36𝑚
Soru 7 : Şekildeki ABCD eğrisel yüzeyine gelen yatay ve düşey bileşke kuvveti bulunuz. (Şekil düzlemine dik genişlik 3 m dir.)
A
1.6 m
2.4 m
Su
Su
B
C
Sonuç:
Fyatay=37.08 kN, Fdüşey=67.59 kN
Çözüm 7:
7
İnşaat Fakültesi
İnşaat Mühendisliği Bölümü
Akışkanlar Mekaniği
Uygulama – IV
Basınç Kuvvetleri
𝑌1 = 2.4𝑥0.6𝑥3𝑥9.81 = 42.38𝑘𝑁
𝑋1 = 1.8𝑥9.81𝑥3 = 52.97𝑘𝑁
𝑋2 = 2.4𝑥9.81𝑥3 = 70.63𝑘𝑁
𝜋𝑥0.62
𝑌2 =
𝑥3𝑥9.81 = 16.68𝑘𝑁
2
𝜋𝑥0.62
𝑥3𝑥9.81 = 8.53𝑘𝑁
4
∑ 𝑋 = 37.08𝑘𝑁
𝑌3 =
∑ 𝑌 = 67.59𝑘𝑁
𝐹 = √𝑥 2 + 𝑦 2 = 77.09𝑘𝑁
Soru 8 : Şekildeki ABC yarım silindirik kapağın şekil düzlemine dik derinliği 5 m dir. Kapağın bir tarafında basınçlı hava vardır. Kapağa
etkiyen hidrostatik itkinin yatay ve düşey bileşenlerini bulunuz.
Sonuç: Fyatay=195.20 kN, Fdüşey=308.23 kN
4m
A
Basınçlı hava
2m
B
2m
4m
2
4.91 N/cm
P=0.5
kg/cm
C
Çözüm 8:
8
2
İnşaat Fakültesi
İnşaat Mühendisliği Bölümü
Akışkanlar Mekaniği
Uygulama – IV
Basınç Kuvvetleri
Düşey kuvvetler:
𝑉=
𝜋 2
𝑥2 𝑥9.81𝑥5 = 308.23𝑘𝑁
2
Yatay kuvvetler:
𝐻 = 𝐻1 + 𝐻2 − 𝐻3
𝐻1 = 4𝑥4𝑥5𝑥9.81 = 784.8𝑘𝑁
4
𝐻2 = 4𝑥 𝑥9.81𝑥5 = 392.4𝑘𝑁
2
𝐻3 = 5𝑥4𝑥49.1 = 982𝑘𝑁
𝐻 = 784.8 + 392.4 − 982 = 195.2𝑘𝑁
Gaz halinde bulunan bir akışkan kapalı bir kap içerisinde basınca maruz kalırsa her nokta da basınç aynıdır.
Soru 9 : Şekildeki hazne sisteminde silindirik kapağa gelen basınç kuvvetini bulunuz. Denge durumu için h2 yüksekliğini diğer verilere
bağlı olarak hesaplayınız. Sonuç:
𝛾
𝜋.𝑑
ℎ2 = ℎ1 (𝛾1 ) + (
2
8
𝛾
) 𝑥 (1 + 𝛾1 )
2
γ2
γ1
h1
h2
D
Silindir Kapak
Çözüm 9:
Yatay kuvvet yok çünkü sağdan ve soldan gelen kuvvetler birbirini götürüyor.
𝜋𝑑2
𝑉1 = (ℎ2 𝑑 −
) 𝛾2
8
𝜋𝑑2
𝑉2 = (ℎ1 𝑑 −
) 𝛾1
8
∑ 𝐹 = 𝑉1 + 𝑉2
Denge hali için
ℎ2 = ℎ1
𝑉1 = 𝑉2 olmalıdır. ℎ2 𝑑𝛾2 −
𝜋𝑑2
8
𝛾2 = ℎ1 𝑑𝛾1 −
𝜋𝑑2
8
𝛾1
𝛾1 𝜋𝑑
𝛾1
+
(1 + )
𝛾2
8
𝛾2
Soru 10: Şekildeki kare şeklinde tasarlanan AB kelebek kapağının açılabilmesi için gereken h derinliğine olmalıdır. Sonuç: h≤11.66 m
(Kapalı kalma şartı)
9
İnşaat Fakültesi
İnşaat Mühendisliği Bölümü
Akışkanlar Mekaniği
Uygulama – IV
Basınç Kuvvetleri
h=?
5.5 m
4.5 m
10 m
Su
A
Su yok
X
B
5.5 m
Mafsal
4.5 m
Kapak
Çözüm 10:
𝐻1 = ℎ𝑥10𝑥10𝑥𝛾𝑠𝑢 = 981ℎ
𝐻2 =
10𝑥10
𝑥10𝑥𝛾𝑠𝑢 = 4905𝑘𝑁
2
𝑀𝑥 = 0
−𝐻1 𝑥0.5 + 𝐻2 𝑥 (4.5 −
10
)=0
3
−490.50ℎ + 5722.50 = 0
ℎ = 11.67𝑚
ℎ > 11.6𝑚
A
Not: Kritik denge durumu için bileşke kuvvetin yeri, kapak milinin üzeri olmalıdır.
Aynı sonuca B noktasına göre moment alınarakta ulaşılabilirdi.
10
B

![1 z)5 = 0 = 1 2 jJ ℎ$ $ = 1 2 jJ [(3.5)$ − (1.5)$] = 49.05](http://s1.studylibtr.com/store/data/003390572_1-cdb355bbc0c5ccdf9fc6d6bf74b2fcd3-300x300.png)