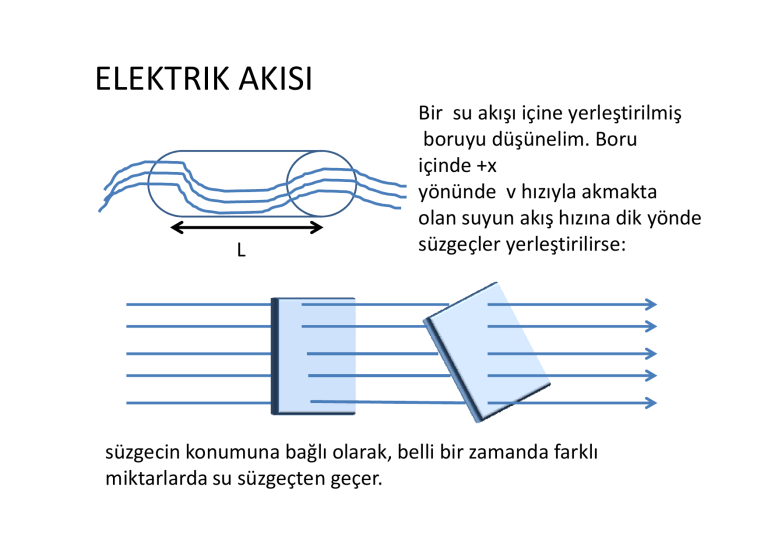
ELEKTRIK AKISI
L
Bir su akışı içine yerleştirilmiş
boruyu düşünelim. Boru
içinde +x
yönünde v hızıyla akmakta
olan suyun akış hızına dik yönde
süzgeçler yerleştirilirse:
süzgecin konumuna bağlı olarak, belli bir zamanda farklı
miktarlarda su süzgeçten geçer.
θ
(a)
(b)
süzgeç suyun akışına dik olarak yerleştirildiğine (a), 1 s de geçen
suyun hacmi
suyun akış hızı x süzgeç kesit alanı = v A olur
Birim zamanda geçen suyun hacmine akı denir.
Süzgeç, süzgeçe normal vektörüyle
akış doğrultusu θ açısı yapacak şekilde (b) yerleştirildiğinde
su miktarı cos θ kadar azalır.
akı = vAcosθ olur.
akı = vAcosθ ifadesinden hareketle akı
Φ=v.A
suyun içinden geçtiği yüzey, faklı yerlerde farklı
konuma sahip düzensiz bir yapı ise
dA
bu durumda akı, sonsuz küçük dA alanlarıdan geçen
akının toplamı olur.
Φ = ∫ v . dA
Su akış çizgileriye elektrik alan çizgileri arasındaki benzerlik
düşünülerek elektrik akısı benzer biçimde yazılabilir.
Φ = ∫ E . dA
Su akışı ile elektrik akısı arasındaki fark, elektrik alanda bir akışın
söz konusu olmamasıdır. Elektrik akısında herhangi bir fiziksel
hareket yoktur.
Bir yüzeyden geçen akı bu yüzeyden geçen elektrik alan çizgilerinin
sayısıyla doğru orantılıdır.
Örnek : Bir küpün yüzeylerinden geçen elektrik akısı
GAUSS YASASI
Kapalı bir yüzeyden (Gauss yüzeyi)
geçen elektriksel akı ile o yüzey
içerisindeki yük dağılımı arasındaki
ilişkiyi ortaya koyar
Gauss yasasının uygulanması için kapalı bir yüzeyden geçen
elektrik akısının bulunması gerekir.
Bu yüzey yük dağılımının geometrisine göre küre ya da silindir
yüzeyi olarak seçilir.
+
-
+
-
içinde net yük bulunmayan kapalı bir
yüzeyden geçen elektrik akısı sıfırdır.
Örnek : Pozitif ߣ çizgisel yük dağılımına sahip, sonsuz
uzunluktaki bir çubuğun elektrik alanın bulunuz.
Örnek : R yarıçaplı Q toplam yüklü küresel kabuk
içinde ve dışında elektrik alanı bulunuz.
ÖDEV 8: Düzgün dağılmış toplam Q yüküne sahip,
R yarıçaplı yalıtkan bir dolu kürenin içindeki ve dışındaki
elektrik alanı bulunuz.