Elektrik Devre Temelleri 3

Elektrik Devre Temelleri
3
TEMEL KANUNLAR-2
Doç. Dr. M. Kemal GÜLLÜ
Elektronik ve Haberleşme Mühendisliği
Kocaeli Üniversitesi
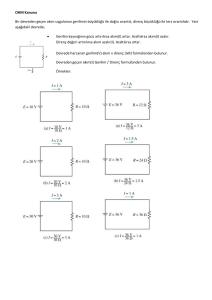
ÖRNEK 2.5
• v1 ve v2 gerilimlerini bulun.
(KGK)
PROBLEM 2.5
• v1 ve v2 gerilimlerini bulun.
ÖRNEK 2.6
• v0 ve i’yi bulun.
(KGK)
Örnek 2.7
• i0 ve v0’ı bulun.
(a düğümüne KAK uygulandığında)
Örnek 2.8
• Şekildeki devre için gerilim ve akımları
bulunuz.
KAK (a düğümü)
KGK (1 çevresi)
KGK (2 çevresi)
2.5. Seri Dirençler ve Gerilim Bölme
Çevrede KGK uygulandığında:
2.5. Seri Dirençler ve Gerilim Bölme
Bu denklem devrenin eşdeğer direnci ile de yazılabilir:
2.5. Seri Dirençler ve Gerilim Bölme
Seri bağlı dirençlerin eş değer direnci her bir
direncin toplamı ile bulunur.
• Devredeki her bir direnç üzerindeki gerilim;
2.5. Seri Dirençler ve Gerilim Bölme
• Dikkat edilirse gerilim, dirençler arasında
büyüklükleri ile doğru orantılı olarak paylaşılmıştır.
• Daha büyük direnç değerli eleman iki ucu arasında
daha fazla potansiyel farkına sahiptir.
• N elemanlı bir devre için:
Gerilim bölme kuralı olarak adlandırılır.
2.6. Paralel Dirençler ve Akım Bölme
• Devredeki dirençler a-b düğümleri
arasına paralel bağlanmıştır
• Dolayısı ile aynı potansiyel farkına
sahiptirler.
veya
• a noktası için KAK yazıldığında:
2.6. Paralel Dirençler ve Akım Bölme
• Req paralel bağlı dirençlerin eşdeğeri ise:
• Paralel bağlı 2 direncin eşdeğer direnci:
• N adet paralel bağlı direncin eşdeğer direnci:
2.6. Paralel Dirençler ve Akım Bölme
• Not: Paralel bağlantıda Req daima en küçük
dirençten daha küçük değerlidir!
• Eğer dirençler eşit ise:
• Paralel bağlı dirençler ile çalışırken direnç
yerine iletkenlik ile çalışmak daha uygun
olabilir:
2.6. Paralel Dirençler ve Akım Bölme
• a düğümüne giren toplam
akım bilinmekte ise i1 ve i2
akımlarını nasıl bulabiliriz?
Akım Bölme Kuralı
2.6. Paralel Dirençler ve Akım Bölme
• Kısa devre ve açık devre
durumlarında:
– Kısa devre:
– Açık devre:
Örnek 2.9
• Req =?
Örnek 2.10
• Req =?
Örnek 2.10
• i0, v0, p0 =?
ya da
2.7. Y- Dönüşümleri
• Şekildeki devrenin eş değer
direncini bulmak için seri ve
paralel bağlanma kuralları
kullanılamıyor
• Bu ve benzeri durumlar için
Y- dönüşümleri kullanılır.
• 3 uçlu eşdeğer devre elde
edilir.
2.7. Y- Dönüşümleri
• Amaç: Devrede bu şekilde bir yapı var ise bu yapıyı
analiz edilebilir diğer yapılara dönüştürmektir.
2.7. Y- Dönüşümleri
(3)
(1)
•  → Y Dönüşümü:
Benzer şekilde:
(2)
2.7. Y- Dönüşümleri
• Benzer şekilde:
• Not: Y devresindeki her bir direnç,  devresinde
komşu 2 daldaki dirençlerin çarpımının , 
devresindeki tüm dirençlerin toplamına oranıdır!
2.7. Y- Dönüşümleri
• Y →  Dönüşümü:
Örnek 2.14
•  → Y dönüşümünü yapın.
2.8. Uygulamalar
ÖRNEK: Şekildeki devrede 9 V luk pil, lambalara
bağlanmıştır.
a) Pilden çıkan toplam akım?
b) Her bir lambadan geçen akım?
c) Her bir lambanın direnci?
ÇÖZÜM: a) Pilin ürettiği güç, lambaların harcadığı güce eşittir.
Devredeki lambalar direnç olarak şekildeki gibi
modellenebilir.
b) R1 direnci üzerinden geçen akım;
KAK üst düğümde uygulanırsa:
c) Her bir lambanın gücü biliniyor öyle ise direnci için;
DC Metre Tasarımı
• Direncin akım sınırlama özelliği farklı uygulamalarda
kullanılır (örn; potansiyometre)
• Potansiyometre (pot) = Potansiyel + metre
• Ayarlanabilir gerilim bölücü:
DC Metre Tasarımı
• Ampermetre, voltmetre,
ohmmetre
– (d’Arsonval metre)
– Bobinden akım geçtiğinde tork
üretilir ve işaretçi hareket eder
– Akım miktarı işaretçinin değişim
miktarını belirler
DC Metre Tasarımı
• Analog ampermetre ve voltmetrenin devreye
bağlanması:
DC Metre Tasarımı
• Analog ampermetre ve voltmetrenin
devreye bağlanması:
•
•
•
•
Voltmetre elemana paralel bağlanır
d’Arsonval hareketini idealde sonsuz
değerli seri bir direnç ile sağlar
Devreden çekilen akım idealde sıfır
olmalıdır
İç direnç pratikte çok büyüktür
fs: full scale (maksimum ölçülecek değer)
Seçilen Vfs için kullanılacak direnç değeri:
DC Metre Tasarımı
• Analog ampermetrenin devreye
bağlanması:
•
•
•
•
Ampermetre elemana seri bağlanır
d’Arsonval hareketini idealde sıfır
değerli paralel bir direnç ile sağlar
Direnç üzerine düşen gerilim idealde
sıfır olmalıdır
İç direnç pratikte sıfıra yakındır
Seçilen Ifs için kullanılacak direnç değeri:
DC Metre Tasarımı
• Direnç Ölçümü:
• 2 şekilde yapılabilir:
• Ampermetre ile üzerinden geçen
akım; voltmetre ile üzerindeki
gerilim ölçülerek
• Ohmmetre ile doğrudan
Yandaki devreye KGK uygulandığında:
Rx=0 yapıldığında Im=Ifs iken R değeri
seçilir. Bu durumda;
DC Metre Tasarımı
• Not: d’Arsonval hareketine bağlı analog ölçü
aletlerinden farklı olarak sayısal ölçüm
aletleri op-amp gibi aktif devre elemanlarını
kullanırlar.
• Sayısal ölçü aletleri değeri ayrık sayılar
şeklinde gösterirken analog ölçü aletlerinde
işaretçi sürekli skalada çalışmaktadır.
Örnek 2.17
• Şekildeki gibi 4 ayrı aralıkta ölçme özelliğine
sahip voltmetreyi aşağıdaki ölçüm aralıkları
için tasarlayın (
)
Örnek 2.17