Bölüm_3_sunu
advertisement

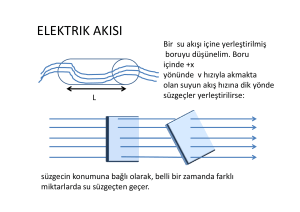
FİZ102 FİZİK-II Ankara Üniversitesi Fen Fakültesi Kimya Bölümü A-Grubu 2016-2017 Bahar Yarıyılı Bölüm-III Özeti 15.03.2017 Ankara A. Ozansoy Bölüm-III: Gauss Kanunu Elektrik Akısı 2. Gauss Kanunu (Yasası) 3. Gauss Kanununun Uygulamaları 4. Elektrostatik Dengedeki İletkenler 1. 2 A.Ozansoy 15.03.2017 1. Elektrik Akısı Soru: Bir bölgede elektrik alan çizgilerinin dağılımını biliyorsak o bölgede yük dağılımını belirleyebilir miyiz? Bilinmeyen miktarda yük içeren bir kutu içerisindeki yük miktarını belirleyebilmek için, E ’ yi kutu yüzeyinde ölçmek yeterlidir. Bunu ölçmenin yolu da bir q0 test yükü üzerindeki kuvveti ölçmektir. 3 A.Ozansoy 15.03.2017 Bir yüzeyden geçen elektrik akısı, elektrik alan çizgilerinin yüzeyden içe veya dışa doğru olması ile ilgilidir. 4 A.Ozansoy 15.03.2017 Elektrik akısının sıfır olduğu 3 durum: 5 A.Ozansoy 15.03.2017 Kutu içindeki yükü 2 katına çıkarmak akıyı da iki kat artırır. Kutunun boyutlarını 2 katına çıkarmak akıyı değiştirmez. Çünkü yüzeyde E ’ nin büyüklüğü (1/4) oranında azalırken, yüzey 4 kat büyümüştür. (Derste çözülen Örnek 3.3’ ü tekrar inceleyiniz.) 6 A.Ozansoy 15.03.2017 Sonuçlar: Kapalı bir yüzeyden geçen elektrik akısının içeri ya da dışarı olması, yüzey içindeki net yükün işaretine bağlıdır. Net elektrik akısı, yüzey içindeki yük miktarıyla doğru orantılıdır ancak yüzeyin boyutlarından bağımsızdır. 7 A.Ozansoy 15.03.2017 Örnek: a) Pozitif yükü çevreleyen küpün yüzeyinden geçen akı nedir? 6 adet alan çizgisi küp yüzeyinden çıktığı için, akı +6 br’ dir. b) Negatif yükü çevreleyen benzer bir küpün yüzeyinden geçen akı nedir? Bu durumda, 6 adet alan çizgisi yüzeyden içeri yöneleceği için, akı -6 br’ dir. Şekil Kaynak [1’] den alınmıştır. 8 A.Ozansoy 15.03.2017 Düzgün elektrik alanın akısı: E E A Düzgün elektrik alanın akısı. A Anˆ Yüzeyden dışarı doğru, yüzeye dik birim vektör. 9 A.Ozansoy 15.03.2017 Düzgün olmayan elektrik alanın akısı: Elektrik alan, seçilen küçük yüzey üzerinde her yerde aynı olacak şekilde yüzey küçük parçalara bölünür. E Ei Ai E lim Ai 0 Ei Ai i Şekil Kaynak[2]’ den alınmıştır. E dA yüzey Elektrik akısının en genel tanımı: E E dA yuzey 10 E cos dA yuzey A.Ozansoy 15.03.2017 (Carl Friedrich Gauss 1777-1855, Alman matematikçi ve gökbilimci) 2. Gauss Yasası Gauss Yasası; yüklü cisimlerin simetrilerinden yararlanarak oluşturdukları elektrik alanı hesaplamayı sağlar. Kapalı bir yüzeyden geçen net elektrik akısı, yüzeyin içindeki net yük miktarı ile doğru orantılıdır. Qiç E E dA 0 Yüzey içindeki net yük Toplam elektrik alan Gauss Yasası, yüzeyin bir noktasındaki elektrik alan ile yüzeyi çevreleyen toplam yük arasındaki ilişkiyi verir. Gauss Yasası, Coulomb Yasasının bir sonucudur. Ancak Gauss Yasası daha geneldir çünkü hareketli yüklere de uygulanabilir. 11 A.Ozansoy 15.03.2017 3. Gauss Yasasının Uygulamaları: Gauss Yasası, yüksek simetriye sahip yük dağılımlarına uygulanır. Sistemin simetrisine uygun bir Gauss yüzeyi seçilir. E ’ yi hesaplayacağımız nokta Gauss yüzeyi üzerinde olmalıdır. Gauss yasası’ nın uygulmaları için üç önemli simetri: Şekil Kaynak[1]’ den alınmıştır. 12 A.Ozansoy 15.03.2017 3.1. Düzgün yüklü yalıtkan küre; 13 A.Ozansoy 15.03.2017 3.2. Sonsuz çizgisel yük dağılımının alanı; E E dA sol E dA sag Qic E dA yan E (2rl ) 14 0 Elektrik alan, yük dağılımından dışarı doğrudur. Sistem silindirik simetriye sahip. E dA E ’ nin tele (ya da çubuk) paralel bileşeni yok. yan (Qiç l ) l E 0 2r 0 Sonsuz tel, bir idealleştirmedir. Eğer alanı hesaplayacağımız mesafe, telin 2k boyutları yanında çok kısa ise Gauss r Yasası yine uygulanabilir. A.Ozansoy 15.03.2017 3.3. Düzgün yüklü sonsuz düzlem levhanın alanı; Elektrik alan levhadan dışarı doğrudur. Gauss Yüzeyi, levhayı iki taraftan saran , levhaya dik bir silindir (ya da dikdörtgen prizma) olabilir. E E dA sol E dA sag E dA sol A.Ozansoy yan Qic E dA sag EA EA 15 E dA 0 A E 0 2 0 15.03.2017 3.4. Zıt yüklü iki düzlem levha: Biri + diğeri - yük yoğunluğu taşıyan iki levha a Levhaların dışında 16 E 0 (a ve c' de) E E1 E2 2 0 2 0 E (b' de) Levhalar arasında 0 A.Ozansoy 15.03.2017 3.4. Düzgün yüklü sonsuz silindirin alanı Hacimsel yük yoğunluğuna sahip, R yarıçaplı sonsuz silindirin içindeki ve dışındaki bölgelerde elektrik alan; (r 2l ) r R E dA E (2rl ) 0 r E 2 0 Şekil, Kaynak[3]’ ten alınmıştır 17 (R 2l ) r R E dA E (2rl ) 0 R 2 E 2 0 r A.Ozansoy 15.03.2017 4. Elektrostatik dengedeki iletkenler: (Bu kısım Kaynak[3]’ ten alınmıştır) 18 A.Ozansoy 15.03.2017 1. İletkenlerin içinde statik elektrik alan bulunmaz. 2. İletkene eklenen fazladan yükler yüzeyde toplanır. E= /0 3. İletkenlerin içine yalıtkan bir boşluk açıldığında, boşluğun içinde yük yoksa, iletken içinde elektrik alan sıfırdır. Boşluğun içinde yük varsa boşluğun dış yüzü indüksiyonla yüklenir, fazla yükler iletken yüzeyinde toplanır ve iletken içinde elektrik alan yine sıfır olur. küresel iletkenin 4. İletkenin hemen dışında E, iletken Yüklü yüzeye diktir ve değeri alanı E= / ’ dır. 0 Gauss yüzeyinin iletkenle arakesiti çok küçük alınırsa , arakesit üzerinde yük yoğunluğu sabit kabul edilir E sabit kabul edilir..! Qic E E dA üst 19 0 A EA E 0 0 A.Ozansoy Lokal yük yoğunluğu 15.03.2017 Örnek: Küresel iletken:. 20 A.Ozansoy 15.03.2017 Kaynaklar: 1. Fizik-İlkeler ve Pratik Cilt-II, E. Mazur (Çeviri Editörleri: A. Verçin ve A.U. Yılmazer) 1. Baskıdan çeviri, Nobel Akademik Yayıncılık, 2016. Ankara. 2. “ Fen ve Mühendislik için Fizik, Cilt-2”, R.A. Serway, R.J. Beichner, 5. baskıdan çeviri, Palme Yayncılık 2002. 3. http://www.seckin.com.tr/kitap/413951887 Fizik”, B. Karaoğlu, Seçkin Yayıncılık, 2012). (“Üniversiteler için 4. Diğer tüm şekiller ; “Üniversite Fiziği Cilt-I “, H.D. Young ve R.A. Freedman, 12. Baskı, Pearson Education Yayıncılık 2009, Ankara 21 A.Ozansoy 15.03.2017