Ders Tanıtım Bilgileri (Türkçe)
1
DERS TANITIM BİLGİLERİ (TÜRKÇE)
Ders Bilgileri
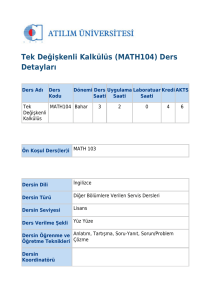
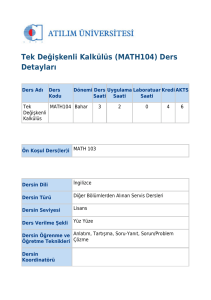
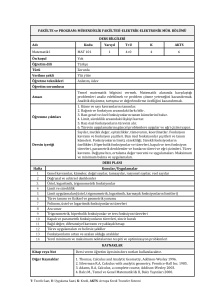
Dersin Adı
Tek Değişkenli
Kalkülüs
Önkoşul(lar)-var
ise
Dersin Dili
Ders Türü
Ders verilme şekli
Dersin Öğrenme ve
Öğretme Teknikleri
Dersin
sorumlusu(ları)
Dersin amacı
Dersin öğrenme
çıktıları
Dersin içeriği
Kaynaklar
Kodu
Yarıyılı
Math Bahar
104
Math 103
Teori
(Saat/Hafta)
Uygulama
(Saat/hafta)
Laboratuar
Yerel
Kredi
AKTS
3
2
0
4
6
İngilizce
Zorunlu
Yüz yüze
Anlatım, Soru-Yanıt, Tartışma, Sorun/Problem çözme
Bu dersin amacı, fonksiyon kavramını, fonksiyon türlerini ve bunların
özelliklerini hatırlamak ve kullanmak, limit, türev ve integral gibi
fonksiyonlar üzerinde yapılan temel işlemleri ve bunların uygulamalarını
anlatmak, ayrıca öğrencilerin problem çözme ve analitik düşünme
yeteneğini geliştirmesi ve gerçek hayat uygulamalarına yönelik becerilerini
artırmaktır.
1) Fonksiyon ve fonksiyon ile ilgili temel kavramları kullanır,
2) Fonksiyonlarda limit kavramını anlar,
3) Türev kavramını anlar, çeşitli fonksiyonların türevini alır,
4) İntegral kavramını anlar, çeşitli fonksiyonların integralini alır,
5) Türev ve integralin uygulamalarını yapar.
Fonksiyon ve fonksiyon ile ilgili temel kavramların hatırlatılması,
Trigonometrik Fonksiyonlar, Üstel ve Logaritma Fonksiyonları, Limit ve
Süreklilik, Türev, Türevin Uygulamaları, Belirli-belirsiz İntegraller, İntegral
Alma Teknikleri, Alan ve Hacim Hesaplama.
Ders Kitabı
B.E. Blank and S.G. Krantz, Single Variable Calculus, 2.ed., John Wiley &
Sons, Inc 2011.
Diğer Kaynaklar
1) J. Stewart, Single Variable Calculus: Early Transcendentals, Brooks Cole, 6
ed., 2007
2) Matematik II, Atılım Üniversitesi Matematik Bölümü Uzaktan Eğitim Ders
Notu
Ders Tanıtım Bilgileri (Türkçe)
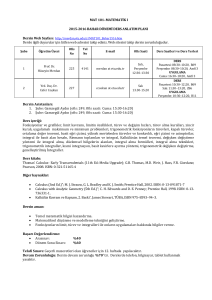
Haftalara göre işlenecek konular
Haftalar
1. Hafta
2. Hafta
3. Hafta
4. Hafta
5. Hafta
6. Hafta
Tartışılacak/işlenecek konular
Fonksiyonların Tekrarı: fonksiyonun tanım, değer
ve görüntü kümeleri; eşit fonksiyonlar; bir gerçel
pp.34-52
değişkenli fonksiyon örnekleri, parçalı fonksiyon,
fonksiyonların grafikleri, diziler, fonksiyonları
birleştirerek yeni fonksiyon elde etme
Ters Fonksiyonlar: Örten, Bire-bir Fonksiyonlar,
Ters fonksiyonun grafiği, dikey ve yatay ötelemeler,
pp. 52-75
Çift ve Tek fonksiyonlar, Parametrelenmiş eğriler
ve
fonksiyonların
grafikleri,
Trigonometrik
fonksiyonlar
Limit kavramı, Limit teoremleri: Tek Yönlü Limitler;
Temel limit teoremleri, Limitin var olmadığını
söyleyen bir kriter, Pinching Teoremi, bazı önemli
pp. 85-108
trigonometrik limitler, Bir sürekli fonksiyonun
tanımı
Sürekli genişletmeler,
tek yönlü süreklilik,
pp. 108-155
Süreklilik üzerine bazı teoremler, Sonsuz limitler ve
Asimtotlar, Üstel fonksiyonlar ve logaritmalar
Değişim hızı ve Teğet doğruları, Türev, Türev pp. 164-200
kuralları
Bazı temel fonksiyonların türevleri, zincir kuralı,
pp. 200-223
Üstel fonksiyonların türevleri, Ters fonksiyonların
türevleri
7. Hafta
Arasınav
8. Hafta
Logaritma fonksiyonlarının türevleri, Logaritmik
türev, Yüksek Basamaktan Türevler, Kapalı
fonksiyonların türevleri, Differansiyeller ve
fonksiyonların
yaklaşımı:
Teğet
Doğrusu
Yaklaştırımı, Differansiyeller
Ters trigonometrik fonksiyonlar, Ters trigonometrik
fonksiyonların türevleri, Bağımlı hız
Ortalama
Değer
Teoremi,
Fonksiyonların
maksimum ve minimum değerleri, uygulamalı
maksimum-minimum problemleri
Konkavlık, Fonksiyonların Grafiklerinin Çizimi,
l’Hopital’s Kuralları
Antidifferentiation ve uygulamaları: Belirsiz
integral, İntegral kuralları, Analiz’in Temel Teoremi
Değişken değiştirme metodu, Alan Hesabı, İntegral
alma teknikleri: Kısmi integrasyon yöntemi
İntegral
alma
teknikleri:
Trigonometrik
Fonksiyonların
kuvvetleri
ve
çarpımları,
Trigonometrik
değişken
değiştirme,
Kismi
9. Hafta
10. Hafta
11. Hafta
12. Hafta
13. Hafta
14. Hafta
Ön çalışma
pp. 223-253
pp. 253-268,282-289
pp. 289-320
pp. 320-348
pp. 357-366, 399-417
pp. 428 - 446, 470-479
pp. 479-506
2
Ders Tanıtım Bilgileri (Türkçe)
15. Hafta
16. Hafta
Kesirler—Doğrusal çarpanlar
İntegral alma teknikleri: Kismi Kesirler — pp. 506-551
İndirgenemez quadratik çarpanlar,
integral
uygulamaları: Hacimler
Genel Sınav
Değerlendirme Sistemi
Yarıyıl İçi Çalışmaları
Sayısı
Devam
Laboratuar
Uygulama
Alan Çalışması
Derse Özgü Staj (varsa)
Ödevler
Sunum
Projeler
Seminer
Ara sınavlar
Genel Sınav
2
1
Toplam 3
Katkı Payı %
60
40
100
60
40
100
Yarıyıl İçi Çalışmalarının Başarı Notuna Katkısı
Yarıyıl Sonu Sınavının Başarı Notuna Katkısı
Toplam
Ders Kategorisi
Temel Meslek Dersleri
Uzmanlık/Alan Dersleri
Destek Dersleri
İletişim ve Yönetim Becerileri Dersleri
Aktarılabilir Beceri Dersleri
AKTS (Öğrenci İş Yükü) Tablosu
Etkinlikler
Ders Süresi ( Sınav haftası dahildir: 16 x
toplam ders saati )
Laboratuvar
Uygulama
Derse özgü staj (varsa)
Alan Çalışması
Sınıf Dışı Ders Çalışma Süresi (Ön Çalışma,
pekiştirme, vb)
Sayısı
Süresi
16
3
Toplam İş
Yükü
48
14
2
28
14
4
56
3
Ders Tanıtım Bilgileri (Türkçe)
Sunum / Seminer Hazırlama
Proje
Ödevler
Ara sınavlara hazırlanma süresi
2
Genel sınava hazırlanma süresi
1
Toplam İş Yükü
13
22
4
26
22
180
Dersin Öğrenme Çıktılarının Program Yeterlilikleri/Çıktıları İle İlişkilendirilmesi
Program Yeterlilikleri/Çıktıları
1
1 Matematik lisans programından edindiği ileri düzeydeki kuramsal ve
uygulamalı bilgileri kullanarak matematik temelli lisansüstü
programlarda, kamu veya özel sektörde bilimsel çalışma ve araştırma
yapmaya yeterli bilgiye sahip olur.
2 Alanında edindiği kuramsal ve uygulamalı bilgileri uygun araçgereçleri kullanarak ortaöğretime uyarlar ve aktarır.
3 Alanında edindiği bilgi ve becerileri kullanarak, matematik veya
uygulandığı alanlardaki güncel problemleri modelleme ve çözüm için
gerekli olan matematiksel yöntemleri seçme, kullanma, geliştirme ve
çözme becerisine sahip olur.
4 Analitik düşünme yeteneğine sahip olur ve sonuç çıkarma sürecinde
zamanı etkin kullanır.
5 Bilgisayar bilimleriyle ilgili alanlarda çalışabilecek düzeyde temel
yazılım bilgisine ve bilişim teknolojilerini etkin bir şekilde kullanma
becerisine sahip olur.
6 Karar süreçlerinin ihtiyaç duyacağı verileri toplama, analiz etme,
yorumlama ve istatistiksel yöntemleri kullanabilme becerisine sahip
olur.
7 Matematiğin doğrudan veya dolaylı olarak kullanıldığı alanlarda
çalışma yapabilecek düzeyde bilgiye sahip olur ve yaşam boyu
öğrenmenin bilinci ile mesleki bilgi ve becerilerini yeniler.
8 Matematiğin kullanıldığı alanlarda bireysel olarak veya takımlarda
ekip üyesi olarak sorumluluk alır ve etkin biçimde çalışma becerisine
sahip olur.
9 Matematik veya uygulama alanlarındaki bilgileri izleyecek ve
meslektaşları ile iletişim kuracak düzeyde İngilizce bilir.
10 Görüş ve düşüncesini nicel ve nitel verilerle destekleyerek açık ve
anlaşılabilir biçimde yazılı ve sözlü ifade eder, paydaşlarıyla iletişim
kurar.
11 Matematik veya uygulama alanları ile ilgili verilerin toplanması,
yorumlanması, uygulanması ve sonuçların duyurulması aşamalarında
Katkı Düzeyi*
2
3
4
5
Ders Tanıtım Bilgileri (Türkçe)
evrensel ve toplumsal boyutlardaki etkilerini dikkate alan mesleki etik
ve sorumluluk bilincine sahip olur.
*Lütfen program yeterliliğine olan katkı düzeyini 0-5 arasında numaralandırarak belirtiniz.
1: En düşük, 2: Düşük, 3: Orta, 4: Yüksek, 5: Çok Yüksek
5