Appendix B: Olasılık ve Dağılım Teorisi

Yıldız Teknik Üniversitesi
İktisat Bölümü
Ekonometri I Ders Notları
Ders Kitabı: J.M. Wooldridge, Introductory Econometrics A
Modern Approach, 2nd. edition, Thomson Learning
Appendix B:
Olasılık ve Dağılım Teorisi
Doç. Dr. Hüseyin Taştan1
1 Yıldız Teknik Üniversitesi, İktisat Bölümü, Yıldız Kampüsü H Blok, Oda no. 124, Beşiktaş, İstanbul.
Email: tastan@yildiz.edu.tr
1
Rassal Değişkenler
(Random Variables)
• Alacağı değer belli bir rassal (random) deneyin
(experiment) sonucuna bağlı olan değişkenlere rassal
değişken (r.d.) denir.
• X: r.d.,
• x: X r.d.’nin aldığı belli bir değer
• Kesikli r.d.: Alacağı değerler sayılabilir (sonlu ya da
sonsuz) olan rassal değişken.
• Sürekli r.d.: Belli bir aralıkta (örneğin reel sayılar doğrusu
üzerinde) herhangi bir değeri alan rassal değişken.
Kesikli r.d.’den farklı olarak sürekli r.d. sayılamaz. Bu
nedenle bir sürekli r.d.’nin belli bir değere eşit olma
olasılığı sıfırdır.
Kesikli Rassal Değişkenler
Kesikli r.d.: Örnek
• Bir basketçinin iki atış yaptığını ve X r.d.’nin başarılı atış
sayısını gösterdiğini düşünelim. X’in alabileceği değerler
kümesi: {0,1,2} olsun. Olasılık fonksiyonu şöyle verilmiş
olsun:
f(0)=0.2, f(1)=0.44, f(2)=0.36
• En az bir başarılı atış olasılığı nedir?
P( X ≥ 1) = P( X = 1) + P ( X = 2)
= 0.44 + 0.36 = 0.80
• Bu dağılımın grafiği şöyledir:
Serbest basket atışı örneği için olasılık fonksiyonu
Sürekli Rassal Değişkenler
•
X sürekli r.d.’nin olasılık yoğunluk fonksiyonu (probability density
function, pdf) aşağıdaki koşulları sağlar:
f ( x) ≥ 0
+∞
∫ f ( x)dx = 1
−∞
•
Aralık olasılıkları:
•
Sürekli r.d.’in aralık olasılıkları şöyle yazılabilir:
Sürekli bir r.d.’nin a ve b arasında olma olasılığı
(taralı bölgenin alanı)
Birikimli Olasılık Fonksiyonu
Aralık Olasılıkları ve Birikimli Olasılık Fonksiyonu
Örnek: X~uniform(a,b)
Ortak (bağlı)dağılımlar (joint distributions) ve
bağımsızlık:
• X ve Y r.d. Aşağıdaki koşul sağlandığında
istatistik bakımından bağımsızdırlar:
• Sürekli:
• Kesikli:
• Sürekli durumda ortak yoğunluklar marjinal
yoğunlukların çarpımı olarak yazılabiliyorsa ya da
kesikli durumda ortak olasılıklar marjinal
olasılıkların çarpımı olarak yazılabiliyorsa bu
değişkenler istatistik bakımından bağımsızdırlar.
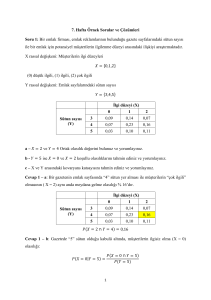
Örnek B.1 : İki serbest basket atışı
•
•
•
•
•
•
•
X :ilk atışın sonucu (1 veya 0)
Y : ikinci atışın sonucu (1 veya 0)
Atıcının genel başarı oranı %80 olsun: Yani, P(X=1)=P(Y=1)=0.80
Basketcinin iki atışı da basket yapma olasılığı nedir?
X ve Y bağımsız (independent) ise,
P(x=1,Y=1)=P(X=1).P(Y=1)=0.8x0.8=0.64
Bağımsız değillerse bu yanıt doğru olmaz.Örneğin, koşullu olasılıkları şöyle
olsun :
Yanıt: (B.15 ) den,
Beklenen Değer (Expected Value)
• E(x) veya µ: X’in tüm muhtemel değerlerinin ağırlıklı bir
ortalamasıdır. Ağırlıklar, olasılık fonksiyonları (ya da
yoğunluk f., pdf) tarafından belirlenir.
• Kesikli:
• Sürekli:
• Örnek : X kesikli r.d. -1,0,2 değerlerini sırasıyla 1/8, ½ ve
3/8 olasılıklarıyla alıyor olsun. Beklenen değerini bulalım.
devam
• X’in bir fonksiyonunun beklenen değeri:
Örnek B.4: Örnek B.3’den, X=-1,0 ve 2 ve olasılıklar,
sırasıyla, 1/8, ½ ve 3/8 idi. g(X)=X2 tanımlayalım.
Böylece,g(X)’in beklenen değeri :
BEKLENEN DEĞERİN ÖZELLİKLERİ
• c sabit bir sayı olmak üzere
• a, b sabit sayılar olmak üzere
• a1,a2,…,an sabit sayılar olmak üzere
• Özel durum: ai=1, her i=1,…,n
Varyans
• X, tesadüfi değişken (random variable), µ=E(X)
olsun.Varyans X rassal değişkeninin, kendi beklenen değeri
çevresindeki değişkenliğinin bir ölçüsüdür.
• Anakütle (population) varyansı ile örneklem varyansı
birbiriyle karıştırılmamalıdır.
• Varyans tanımı:
Aynı ortalamaya fakat farklı dağılımlara (varyansa) sahip iki
değişken : x ve y
Varyansın Özellikleri
• Eğer P(X=c)=1 ise Var(X)=0, E(X)=c
• Yani bir rassal değişkenin varyansı sıfırsa aslında o r.d.
bir sabit sayıdır. Başka bir deyişle, sabit bir sayının
varyansı sıfırdır.
• a ve b sabit sayılar olmak üzere
• Bir rassal değişkene sabit bir sayının eklenmesi o r.d.’nin
varyansını değiştirmez.
• Bir rassal değişken sabit bir sayıyla çarpılırsa, varyansı
sabitin karesiyle çarpılır.
Standart sapma
• Bir rassal değişkenin standart sapması o r.d.’nin
varyansının pozitif kareköküdür.
• Sabit bir sayının standart sapması sıfırdır.
• a ve b sabit sayılar olmak üzere
Bir değişkenin standardize edilmesi
• Rassal değişken X’in ortalaması µ ve standart
sapması σ olsun. X’in ortalamasından sapmalarını
standart sapmasına bölerek yeni bir Z değişkeni
tanımlayalım:
Kovaryans
• X ve Y tesadüfi değişkenlerinin beklenen
değerlerine,
ve
, diyelim.
• Kovaryans, X ve Y r.d.’lerinin ortalamalarından
farklarının çarpımının beklenen değeri olarak
tanımlanır:
Kovaryansın Özellikleri
• X ve Y bağımsız ise kovaryansları sıfırdır.
• Ancak bunun tersini söyleyemeyiz. Yani
kovaryansın sıfır olması X ve Y’nin bağımsız
olduğu anlamına gelmez.
• a, b sabit sayılar olmak üzere
• Cauchy-Schwartz eşitsizliği
Korelasyon katsayısı: doğrusal bağımlılık (linear
dependence) ölçüsü
• X ve Y bağımsız ise korelasyon katsayısı 0 olur.
• Korelasyon katsayısının 0 olması X ve Y’nin bağımsız
olduğu anlamına gelmez. Bu durumda X ve Y ilişkisizdir
(uncorrelated) denir.
• Korelasyon katsayısının işareti kovaryansın işaretine
bağlıdır.
• Nedensellik ilişkisi belirtmez.
Korelasyon (devam)
►
Tesadüfi değişkenlerin toplamlarının varyansı
• a ve b sabit sayılar olmak üzere
• X ve Y r.d. bağımsız ya da ilişkisiz ise sondaki
Kovaryans terimi sıfır olur ve:
devam
►
ve
Özel durum:
ikili olarak ilişkisiz rassal değişkenler
sabit sayılar olmak üzere
Koşullu beklenen değer (conditional
expectation)
• Korelasyon ve kovaryans iki değişken arasındaki
doğrusal (linear) ilişkiyi ölçer ve değişkenleri
simetrik olarak ele alır. X ile Y aynı konumdadır.
Oysa, çoğu kez, X’i bağımsız, Y’yi bağımlı değişken
alarak, belli bir X değeri verilmişken Y’nin alacağı
değeri bulmak isteriz. İlişki, doğrusalolmayan(nonlinear) türden olacaktır.
• Koşullu beklenen değer kovaryans ve korelasyon
katsayısının yakalayamayacağı doğrusal olmayan
ilişkileri de gösterir.
• Bu durumda tek bir sayıdan ibaret bir ölçü
bulamayacağız.Onun yerine, X’in verilmiş değerleri
için Y’nin koşullu beklenen değerine (conditional
expectation or conditional mean) bakacağız.
devam
►
•
•
•
Burada, ağırlıklar X’in aldığı değerlere göre değişen
olasılıklar olmaktadır. E(Y|x), x’in bir fonksiyonudur ve
Y’nin beklenen değerinin x ile birlikte nasıl değiştiğini
gösterir.
Örnek : X, eğitim durumu değişkeni (okunulan yıl sayısı),
Y, saat başına ücretler. Ülkedeki tüm çalışanlar
kapsanmaktadır (örnek değil kitle söz konusu)
Aşağıdaki grafik, tahsile göre ücretlerin beklenen değerini
verecektir.
devam
• öyle bir doğrusal ilişki bulunmuş olsun:
Koşullu beklenen değerin özellikleri
1.
c(X), X’in herhangi bir fonksiyonu olsun:
E[c(X)|X] = c(X)
Eğer X’e göre koşullu beklenti alıyorsak, X’in fonksiyonları
sabit gibi düşünülebilir (sabitin beklenen değeri
kendisine eşittir).
Örnek: E[X2|X] = X2
2. X’in a(X) ve b(X) gibi iki fonksiyonu için:
E[a(X)Y+b(X)|X] = a(X)E[Y|X] +b(X)
Örnek: XY+2X2’nin X’e göre koşullu beklenen değerini
bulalım:
E[XY+2X2|X] = X E[Y|X] + 2X2
devam
3.
X ve Y bağımsız ise
E(Y|X) = E(Y)
X ve Y bağımsızsa Y’nin X’e göre koşullu beklenen değeri
X’e bağlı değildir. X’in değeri ne olursa olsun Y’nin
koşullu beklentisi koşulsuz beklentiye eşit olur.
Örneğin, ücret-eğitim ilişkisinde eğer ücretler eğitim
düzeyinden bağımsız olsaydı ilkokul ve üniversite
mezunlarının ücret ortalamaları aynı olurdu. Ancak bu
doğru olmadığından ücret ve eğitim seviyesinin
bağımsız olduğunu varsayamayız.
Bu özelliğin özel bir durumu şudur: Eğer U ve X
bağımsızsa ve E(U)=0 ise:
E(U|X) = 0
devam
4.
Yinelenen Beklentiler Kanunu (Law of Iterated
Expectations)
E[E(Y|X)] = E(Y)
Anlamı: Eğer önce E(Y|X)’i X’in bir fonksiyonu olarak
hesaplar, daha sonra X’in dağılımına göre beklentisini
alırsak Y’nin beklenen değerine ulaşırız.
Bu özelliğin daha genel bir versiyonu:
E(Y|X) = E[E(Y|X,Z) |X]
5. Eğer E(Y|X) = E(Y) ise Cov(X,Y)=0 ve Corr(X,Y)=0
X’in her fonksiyonu Y ile ilişkisizdir.
U ve X iki r.d. olsun. E(U|X) = 0 ise (4) ve (5) özelliklerinden
hareketle E(U)=0’dir ve U ve X ilişkisizdir (kovaryansları
sıfırdır)
Koşullu Varyans
(Conditional Variance)
• Y’nin X’e göre koşullu varyansı ilgili koşullu dağılımdan
hareketle hesaplanan varyanstır:
Var(Y|X=x) = E{[Y-E(Y|x)]2 |x}
= E(Y2|x) –[E(Y|x)]2
• Eğer X ve Y bağımsızsa
Var(Y|X) = Var(Y)
Normal (Gaussian) Dağılım
• X sürekli rassal değişkeni normal dağılıma uyuyorsa
herhangi bir değeri alabilir.
• Normal dağılımın iki parametresi vardır: beklenen değer
ve varyans:
µ=E(X) ve σ2=Var(X)
• Olasılık yoğunluk fonksiyonu (pdf):
Normal Dağılımın oyf’nun grafiği
Ki-kare Dağılımı
• Zi, i=1,...,n, birbirinden bağımsız standart normal r.d.
olsun. Bunların karelerinin toplamı n s.d. ile ki-kare
dağılımına uyar.
t-Dağılımı
•
Z std normal dağılan, X ise n s.d. ile ki-kare dağılan birbirinden bağımsız
iki r.d. olsun. Bu durumda aşağıdaki r.d. n. s.d. ile t dağılımına uyar:
F Dağılımı
• X1 k1 s.d. ile X2 ise k2 s.d. ile ki-kare dağılımına uyan
birbirinden bağımsız iki r.d. olsun. Bu durumda aşağıdaki
r.d. (k1,k2) s.d. ile F dağılımına uyar: