ÖDEV 1

A.Ü. SBF, IV Maliye
EKONOMETRİ I
ÖDEV I
Ödevle ilgili bilgi yoklaması 6 Ekim 2015 Salı, Saat 15:30’da yapılacaktır.
1) Aşağıdaki ifadeler doğru mu, yanlış mı, belirsiz midir?
a) Ailenizin 2013 yılında elde ettiği gelir rassal değişkendir.
b) Sınıftan rastgele seçilecek bir öğrencinin ailesinin 2013 yılı geliri rassal değişkendir.
2) Aşağıda olasılık dağılımı verilen X rassal değişkeninin beklenen değer ve varyanslarını
bulunuz.
X
-1
0
1
PX(x)
0.25
0.50
0.25
3) Rassal bir değişkenin beklenen değeri (veya ortalaması) ve standart sapması bu değişken ile ilgili
olarak ne tür bilgi vermektedir? Diğer bir deyişle bu ölçütlerden ne öğrenilebilir?
4) X, ortalaması X ve standart sapması x olan kesikli bir rassal değişken olsun. Yeni bir Z
değişkeni Z = a + bX olarak tanımlanmıştır. Burada a = -X/x ve b = 1/x ise (X ve x
sabit sayılardır) Z rassal değişkeninin ortalama ve standart sapmasını bulunuz.
5) X değişkeni 0, 1 ve 2 değerlerinden birini, X değişkeni de 1 ve 2 değerlerinden birini
alabilmektedir. Bu değişkenlerin bileşik olasılık dağılımı aşağıdaki tabloda verilmiştir.
Y↓ X→
0
1
2
0
0.4
0.1
0.0
1
0.3
0.2
0.0
a) Bu değişenler için kovaryansı hesaplayınız ve yorumlayınız.
b) Var(Y|X=1) koşullu varyansını hesaplayınız
6) XN(12 , 4) ise X in 9 ile 13 arasında bir değer alma olasılığını hesaplayınız.
7) Ortalaması 1455, standart sapması 50 olan 2500 gözlemlik örneklem sonucuna dayanarak
anakütle için H0 :  = 1500, H1 :  1500 hipotezini %5 anlamlılık düzeyinde test ediniz.
Yaptığınız bir varsayım varsa belirtiniz.
8) Ortalaması μ, varyansı σ2 olan bir anakütleden seçilen üç gözlemli rassal örneklem X1, X2
ve X3 olsun. μ'nün aşağıdaki iki nokta tahmin edicisini ele alalım:
X1  X 2  X 3
X  4X 2  X 3
ˆ 2  1
3
6
a) Her iki tahmin edicinin de sapmasız olduğunu gösteriniz.
b) Hangi tahmin edici daha etkindir?
ˆ 1 
MATEMATİK ALIŞTIRMALAR
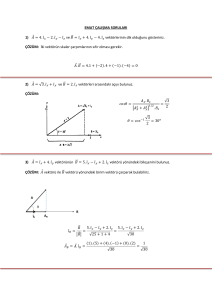
1) y = 5 + 4x – x2 fonksiyonunun varsa göreli uçdeğerlerini bulunuz, bu değerlerin maksimum
mu, minimum mu olduğunu belirtiniz.
 u1 
1 2
 
1 0 0 
 7 1 0 
u 
1 5
 
a


2



 
, x   , y 
4 
2) A  
 b  , k   4 2 5 , u     , h   1 1
1 3

 
2 1 3
13  3  4
 


 
1 1 

u n 
a) Yukarıdaki matrisler için şu çarpımlardan tanımlı olanları hesaplayınız:
Ay, Ay’, xy’, y’y, xk, u’u
b) Yukarıdaki matrislerden varolanlar için ters matrisi bulunuz.
c) k ve h matrislerinin rankını bulunuz.
3) Aşağıdaki denklem sistemini matrislerle ifade ediniz ve ters matris yöntemiyle x, y ve z’nin
çözümlerini bulunuz.
5=x
1 = 4x + 2y + 5z
-2 - y = 2x + 3z