3. EĞİK DÜZLEMDE HAREKET Hazırlayanlar Arş. Grv. M

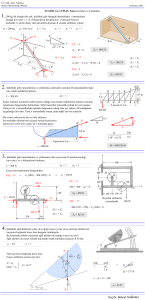
3. EĞĐK DÜZLEMDE HAREKET
Hazırlayanlar
Arş. Grv. M. ERYÜREK
Arş. Grv. H. TAŞKIN
AMAÇ
Eğik düzlemdeki ivmeli hareketi gözlemek ve bu hareket için yol-zaman, hız-zaman
ilişkilerini incelemek, yerçekimi ivmesini ve eğik düzlem ile sürtünme katsayısını ölçmek.
ARAÇLAR
Eğik düzlem ,tahta blok, cetvel, kronometre, dinamometre.
GĐRĐŞ
Bir cismin ortalama hızı onun birim zamanda aldığı yol olarak tanımlanır. Yani cisim bir ∆t
süresince ∆x kadar yer değiştirmiş ise ortalama hızı
vort =
∆x
∆t
(1)
x
x
2
∆x
olarak tanımlanır.
Hızın sabit olduğu (zamanla değişmediği) bir harekette yol-
x
1
t
zaman grafiği Şekil 1' de görüldüğü gibi bir doğrudur.
x 2 − x1
∆x
=
t 2 − t1
∆t
1
t
t
2
Şekil 1. Sabit hızla hareket
eden cismin yol-zaman
grafiği.
Bu doğrunun eğimi cismin sabit v hızını verir.
v = tan θ =
θ
∆t
(2)
Böylece hızın sabit olduğu bir hareket için yol-zaman grafiğinin denklemi
(3)
x = vt
olacaktır.
Hızın sabit olduğu durumdaki hız zaman grafiği ise Şekil 2’ deki gibi zaman eksenine paralel
bir doğru olacaktır. Bu grafik bize hızının zamanla değişmediğini, sabit kaldığını
anlatmaktadır.
31
Hızın sabit olmadığı (zamanla değiştiği) hareketlere ivmeli hareketler denilmektedir.
v
Eğer bir cismin hızı zamanla doğrusal olarak artıyor ya da
azalıyorsa cismin bu hareketine sabit ivmeli hareket
v
denilmektedir.
Böylece ivme birim zamandaki hız değişimi, yani
t
Şekil 2. Sabit hızla
hareket eden cismin
(4)
hız-zaman grafiği.
olarak tanımlanmaktadır. (Eğer hız zamanla azalıyorsa bu durumda cisim negatif ivmeli bir
hareket yapıyordur.)
Sabit ivmeli bir harekette yol-zaman grafiği eğer ilk hız sıfır ise Şekil 3’ deki gibi bir parabol
olur.
x
Bu parabolün denklemi
x=
1
2
at 2
(5)
∆x
θ
biçimindedir. Görüldüğü gibi burada alınan yol zamanla
0
∆t
t'
t
doğrusal olarak değil zamanın karesiyle orantılı olarak
Şekil3. Sabit ivmeli hareket
artmaktadır.
yapan bir cismin yol-zaman grafiği
Eğer cismin herhangi bir andaki hızını (anlık hız veya
ani hız) bulmak istersek, yol-zaman eğrisinde göz önüne aldığımız, bu zamana karşılık gelen
noktadaki “teğetin eğimini” hesaplamamız gerekir.
v
Böylece Şekil 3' deki t' anı için ani hız
v( t ') = tan θ =
∆x
(6)
∆t
bağıntısından hesaplanır.
v(t')
v
2
v
1
θ
Đlk hızın sıfır olduğu bir ivmeli harekette hız-zaman
t
t
t
grafiği ise hız zamanla doğrusal olarak arttığından Şekil
t'
1
2
4’ deki gibi bir doğru olur. Bu doğrunun denklemi
Şekil 4. Sabit ivmeli hareket
v = at
(7)
yapan cismin hız-zaman grafiği.
32
biçimindedir. Bir t anındaki anlık hız v( t') grafikten doğrudan bulunabilmektedir. Bu
doğrunun eğimi de bize hareketin ivmesini verecektir.
v − v1 ∆v
a = tanθ = 2
=
t2 − t1
∆t
(8)
Hızın zamanla doğrusal olarak değişmediği hareketlerde vardır. Bu tür hareketlere değişken
ivmeli hareketler denilmektedir. Şekil 5’ deki hız-zaman grafiği değişken ivmeli bir harekete
aittir.
v
∆V
θ
∆t
t
t'
Şekil 5. Değişken ivmeli bir hareket için hız-zaman grafiği.
Burada herhangi bir t' anındaki ivme (ani ivme) t' anına karşılık gelen noktadaki teğetin
eğiminin hesaplanmasıyla bulunur. Yani
a( t ') = tan θ =
∆v
(9)
∆t
olur.
SÜRTÜNME KUVVETĐ, STATĐK SÜRTÜNME KUVVETĐ
Sürtünme kuvvetinin daha iyi anlaşılabilmesi için basit bir deney yapmak faydalı olacaktır.
F
(a)
(b)
Şekil 6a-6b. Sürtünme kuvvetinin belirlenmesi için gerekli deney düzenekleri
Bunun için size verilen bir tahta bloğu, tahta zemin üzerine yerleştiriniz. Tahta bloğa bir
dinamometreyi
tutturunuz
(Şekil
6a).
Dinamometrenin
ucundan
yavaşca
çekiniz,
uyguladığınız kuvvetin bloğu harekete geçirmediğini göreceksiniz. Newton 'un ikinci
yasasına göre bir cisim, uygulanan kuvvetin etkisi ile ivmeli hareket yapmalıdır. Bu durumda
cisim hareket etmediğine göre cisme etki eden net kuvvet sıfırdır (eylemsizlik prensibi).
Ancak görünen tek kuvvet sizin uyguladığınız kuvvettir. Burada cismin hareketini engelleyen
ve uygulanan kuvvete zıt yönde yönelmiş bir kuvvetin varlığı söz konusudur. Đşte bu kuvvete
33
sürtünme kuvveti denir. Sürtünme kuvveti her zaman hareketi engelleyici yöndedir. Yatay
bir yüzey üzerinde duran bir cismi harekete geçirmek için üzerinde bulunduğu yüzeye paralel
doğrultuda uygulanması gereken minimum kuvvet statik sürtünme kuvvetine eşit olmalıdır.
Bu tanımlara göre statik sürtünme kuvvetini kolayca ölçebilirsiniz. Bunun için cisme
uyguladığınız kuvveti arttırınız. Cismin harekete başladığı andaki kuvveti dinamometreden
okuyunuz. Ölçtüğünüz kuvvet statik sürtünme kuvvetine eşittir. Böylece tahta yüzeyin cisim
üzerine uyguladığı sürtünme kuvvetini bulmuş olursunuz. Yapılan deneyler sürtünme
kuvvetinin, sürtünen yüzeyleri sıkıştıran normal kuvvetle orantılı ve yüzeylerin cinsine ve
fiziksel durumuna bağlı olduğunu göstermişlerdir. k sürtünme katsayısı, N normal kuvvet
olmak üzere sürtünme kuvveti;
Fs=kN
(10)
N
dir. Şekil 7’ ye göre N=W=mg, F=Fs olduğundan
cismin kütlesi biliniyorsa sürtünme katsayısı
Fs
kolayca bulunabilir. Eşitlik (10)’ da görüldüğü gibi
F
sürtünme kuvveti sürtünen yüzeylerin büyüklüğüne
W
Şekil 7. Sürtünmeli yüzey üzerindeki
cisme etkiyen kuvvetlerin gösterimi
bağlı değildir. Bunu görebilmek için cismin farklı
bir yüzeyini tahta düzleme oturtunuz ve yaptığınız
işlemleri tekrarlayarak, sürtünme kuvvetini ve
katsayısını bulunuz. Elde ettiğiniz değerlerin birbirlerine yakın olduğunu göreceksiniz.
SÜRTÜNMELĐ, SÜRTÜNMESĐZ EĞĐK DÜZLEM
Bilindiği gibi yeryüzü yakınında serbest düşmeye bırakılan tüm cisimler sabit g = 9.80 m/s2
ivmesi ile düşerler. Serbest düşme hareketi ayrıntıları ile kolayca gözlenemeyecek kadar hızlı
bir harekettir. Bu nedenle yapacağımız deneyde yerçekimi ivmesini ölçebileceğimiz eğik
düzlem deney düzeneğini kullanacağız.
N=mgcos θ
F=mgsin θ
h
θ
N`=mgcos θ
W=mg
θ
D
Şekil 8. Sürtünmesiz eğik düzlem.
34
Şekil 8' deki sürtünmesiz eğik düzlemi göz önüne alalım. Burada m kütleli cismi hareket
ettiren kuvvet onun W=mg ağırlığının düşey bileşeni olan
(11)
F = mg sin θ
kuvvetidir. W=mg ağırlığının yatay bileşeni olan N' = mg cos θ kuvveti ise sadece cismi
yüzeye bastırmaya çalışır, yani harekete bir etkisi yoktur. N = mg cos θ kuvveti, bu kuvveti
dengeleyen bir tepki kuvveti olarak ortaya çıkar.
Newton' un 2. yasası cisme etki eden kuvvetin
F=ma
(12)
ya eşit olacağını söyler. Böylece denklem (11) ve denklem (12) in birbirlerine eşitlenmesi ile
kayma ivmesi için,
(13)
a = g sin θ
ifadesi bulunur. Görüleceği gibi kayma ivmesi a daima g yerçekimi ivmesinden küçük
olmaktadır. Çünkü sinθ daima 1 den küçüktür.
Şimdi de Şekil 9' daki sürtünmeli eğik düzlemi gözönüne alalım. Burada cismi harekete
geçiren net kuvvet artık F = mg sin θ değil
Fnet = mg sin θ − Fs = mg sin θ − kmg cos θ
(14)
N=mgcos θ
Fs=kN
F=mgsin θ
h
θ
N`=mgcosθ
θ
W=mg
D
Şekil 9. Sürtünmeli eğik düzlemde bir cismin serbest cisim diyagramı.
kuvvetidir. Çünkü sürtünme kuvveti harekete daima zıt yönlüdür ve idealize edilmiş şekliyle
sadece normal kuvvete ve birbiri üzerinde kayan maddelerin cinsine bağlıdır. Temas
yüzeyinin alanına ve hıza bağlı değildir (k, sürtünme katsayısıdır). Denklem (14)’ ün ma 'ya
eşitlenmesiyle cismin sürtünmeli eğik düzlemdeki kayma ivmesi
a = g( sin θ − k cos θ)
(15)
35
olarak hesaplanır.
Eğer net kuvvet Fnet=0 ise Newton'un 2. yasası gereği cisim ya durgun kalacaktır ya da küçük
bir itmeyle sabit hızla (ivmesiz) kaymaya başlayacaktır. Net kuvvetin sıfıra eşitlenmesiyle
sınır açısı yani cismin tam kaymaya başladığı andaki açı;
θs = tan −1( k )
(16)
olarak hesaplanır.
DENEYĐN YAPILIŞIYAPILACAK ĐŞLER
1.Statik Sürtünme Kuvveti ve Sürtünme Katsayısının Bulunması: Terazi yardımıyla
bloğun kütlesini ölçünüz. Tahta bloğu düzleme yerleştiriniz ve dinamometre yardımıyla üç
farklı statik sürtünme kuvvet değerlerini tespit ederek ölçümleri deney raporuna yazınız .
2.Sürtünmeli Eğik Düzlemde Sınır Açısının Belirlenmesi: Tahta bloğunuzu eğik
düzleminiz üzerinde bir konuma yerleştiriniz. Eğik düzlemi üzerinde bulunan vida aracılığı
ile yükseltiniz.(tahta bloğu yükseltirken yavaş hareket ediniz.) Tahta bloğun kaymaya
başladığı andaki yükseklik için beş farklı değeri deney raporuna yazınız. Burada önemli olan
tahta bloğu her ölçüm için eğik düzlemin farklı noktalarına yerleştirmenizdir, çünkü sürtünme
katsayısı eğik düzlem üzerinde her noktada farklı olabilir.
3.Sürtünmeli Eğik Düzlemde, Alınan Yolun Zamana Bağımlılığının Đncelenmesi
Eğik düzlemin eğim açısını ayarlayınız.(eğim açısını 2.kısımda hesapladığınız sınır açısından
büyük bir değere ayarlayınız. Neden böyle bir seçim yapıldığını deney raporunun sonuçyorum bölümünde yorumlayınız.) Tahta bloğu daha önceden belirlenmiş (x= 20,40,60,80,100
cm) beş farklı konumdan kaymaya bırakınız ve kronometre yardımı ile her nokta için dört kez
iniş sürelerini ölçünüz. Ölçtüğünüz bu değerleri deney raporuna yazınız.
VERĐLERĐN ÇÖZÜMLENMESĐ
1. Ölçtüğünüz farklı statik sürtünme kuvveti değerlerinden ve tahta bloğun kütlesinden
yararlanarak gerekli bağıntılar yardımıyla her bir veri için sürtünme katsayını
hesaplayarak ortalama değerini bulunuz.
2. Ölçtüğünüz farklı yükseklik değerleri (h) ile bu yükseklik değerlerine karşılık gelen
taban uzunlukları için sınır açısını hesaplayınız ve sürtünme katsayısını bulunuz.
3. Ölçtüğünüz t değerleri için x-f(t) ve x-f(t2) grafiklerini çiziniz. Grafiğin eğiminden tahta
bloğun ivmesini hesaplayınız.gerekli bağıntılardan yararlanarak g yerçekimi
ivmesini bulunuz ve bilinen değer ile karşılaştırınız.
36
KAYNAKLAR
1. D. Halliday -R. Resnick , Temel Fizik ( çeviri)
2. Richards Sears,Werh Zemansky, Modern Üniversite Fiziği (çeviri)
3. Đsmet Ertaş , Denel Fizik Dersleri, Ege Üni. Basımevi
4. Enis Erdik , Mekanik ve Maddenin Özellikleri, Ank. Üni. Fen Fak. Yayınları
37