PowerPoint Sunusu - Başkent Üniversitesi

TBF 121 - Genel Matematik I
DERS – 12: Belirli İntegral
Prof. Dr. Halil İbrahim Karakaş
Başkent Üniversitesi
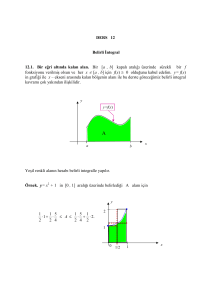
Bir eğri altında kalan alan. Bir [a , b] kapalı aralığı üzerinde sürekli bir f fonksiyonu
verilmiş olsun ve her x  [a , b] için f(x)  0 olduğunu kabul edelim. y = f(x) in grafiği ile
x – ekseni arasında kalan bölgenin alanı ile bu derste göreceğimiz belirli integral kavramı
çok yakından ilişkilidir.
y
y
y=f(x)
2
1
A
a
b
x
0 1/2
1
Yeşil renkli alanın hesabı belirli integralle yapılır.
Örnek. y = x2 + 1 in [0 , 1] aralığı üzerinde belirlediği A alanı için
1
1 5
1 5 1
 1    A     2  9  A  13
2
2 4
2 4 2
8
8
x
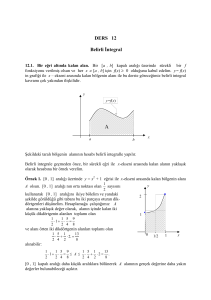
Belirli İntegral, Riemann Toplamları. Bir [a , b] kapalı aralığı üzerinde sürekli bir f
fonksiyonu verilmiş olsun.
y
(c1 , f(c1))
a=x0 < x1 < x2 < x3 < . . . < xn-2 < xn-1 < xn=b
ck  (xk-1 , xk) , 1  k  n
xk = xk – xk-1 , 1  k  n
c2
c1
x0 = a
x1
cn-2
c3
x2
x3
xn-3
cn-1
xn-2
cn
xn-1
b =xn
x
y = f(x)
Tn = f(c1)  x1 + f(c2)  x2 + . . . + f(cn)  xn =
denir.
n
 f (c )x
k 1
k
k
toplamına bir Riemann Toplamı
y
(c1 , f(c1))
a=x0 < x1 < x2 < x3 < . . . < xn-2 < xn-1 < xn=b
ck  (xk-1 , xk) , 1  k  n
xk = xk – xk-1 , 1  k  n
c2
c1
x0 = a
x1
cn-2
c3
x2
x3
xn-3
cn-1
xn-2
cn
xn-1
b =xn
x
y = f(x)
Riemann Toplamı:
Tn = f(c1)  x1 + f(c2)  x2 + . . . + f(cn)  xn =
 xk
n
 f (c )x
k 1
k
k
lardan her biri sıfıra yaklaşırken (ki bu durumda n sayısı da sonsuza ıraksar) Tn
Riemann Toplamı’nın limit değerine f fonksiyonunun [a , b] kapalı aralığı üzerinde belirli
integrali (definite integral) denir ve bu integral
sembolü ile gösterilir.

b
a
f (x) dx
integralin üst sınırı
integralin alt sınırı
y
(c1 , f(c1))
a=x0 < x1 < x2 < x3 < . . . < xn-2 < xn-1 < xn=b
ck  (xk-1 , xk) , 1  k  n
xk = xk – xk-1 , 1  k  n
c2
c1
x0 = a
x1
cn-2
c3
x2
x3
xn-3
cn-1
xn-2
cn
xn-1
b =xn
y = f(x)
Riemann Toplamı:
n
Tn = f(c1)  x1 + f(c2)  x2 + . . . + f(cn)  xn =
 f (c
k 1
k
)x k
Belirli İntegral:

b
a
f (x) dx  lim Tn
x k 0
 lim
x k 0
 f (c1 )x1  f (c2 )x2    f (cn )xn 
x
Eğer her x [a , b] için f(x)  0 ise,
b
 f (x)dx
belirli integrali [a , b] aralığı üzerinde
y = f(x) in grafiği ile x – ekseni arasında kalan alanı verir.
a
y
y = f(x)
b
A   f (x) dx
A
a
f(x)  0
a
b
, x  [a , b]
x

b

b
Eğer her x [a , b] için f(x) ≤ 0 ise, ( f (x))dx   f (x) dx belirli integrali [a , b] aralığının
a
a
altında y = f(x) in grafiği ile x – ekseni arasında kalan alanı verir.
y
a
b
x
A
y = f(x)
f(x)  0
, x  [a , b]
b
A    f (x) dx
a
Genel Durum:
y
A
a
C
c
d
b
x
B
y = f(x)
b
c
d
b
a
c
d
a f (x)dx  A  B  C   f (x)dx   f (x)dx   f (x)dx
y
(c1 , f(c1))
a=x0 < x1 < x2 < x3 < . . . < xn-2 < xn-1 < xn=b
ck  (xk-1 , xk) , 1  k  n
xk = xk – xk-1 , 1  k  n
c2
c1
x0 = a
x1
cn-2
c3
x3
x2
xn-3
cn-1
xn-2
cn
xn-1
b =xn
x
n
Tn   f (ck )x k
y = f(x)
k 1
Özellikler:
• 1. Eğer her x [a , b] için f(x)  0 ise,
b
 f (x)dx
a
belirli integrali [a , b] aralığı üzerinde
y = f(x) in grafiği ile x – ekseni arasında kalan alanı verir.
• 2.
 k  f (x)dx  k  f (x)dx
• 3.
  f (x)  g(x)dx  f (x)dx   g(x)dx
b
b
a
a
b
b
b
a
a
a
• 4. a < c < b için
b
c
b
a
a
c
 f (x)dx  f (x)dx   f (x)dx
Kalkülüs’ün Temel Teoremi(Fundamental Theorem of Calculus). Bu teorem belirli integral ile
belirsiz integral arasındaki ilişkiyi verir:
Kalkülüs’ün Temel Teoremi. f fonksiyonu [a , b] kapalı aralığında sürekli ve
f nin bir ters türevi F ise,
b
 f (x)dx  F (b)  F (a)
a
dir.
Kalkülüs’ün Temel Teoreminden belirli
integral için bir özellik daha yazabiliriz:
b
F (x) a  F (b)  F (a)
Gösterim.
F ' (x)  f (x) 
Örnek.
0 2x  1dx 
1
• 5.
b
a
a
b
 f (x)dx    f (x)dx
b
b
f
(
x
)
dx
 F (x) a  F (b)  F (a)
a
x  x  1  1  0  0   2.
2
1
0
Kalkülüs’ün Temel Teoremi. f fonksiyonu [a , b] kapalı aralığında sürekli ve
f nin bir ters türevi F ise,
b
b
a
a
 f (x)dx  F (x)
 F (b)  F (a)
dir.
Örnek.
1
x3
4
1 
2


x

1
dx




x


1

0

0

.


0
3
3
3 
0
1
y
2
y = x2+1
4
A   x 2  1dx  .
0
3
1
1
A
0
1
x
4
2

x
x
2
2
x

3
e

dx

 x  3e  4 ln x
1 
1
x
 4  3e 2  4 ln 2  1  3e  0 
2
 3(1  e 2  e)  4 ln 2.

6
0
2x
dx  ?
x2  4
u = x2 + 4


6
0
, du = 2x dx .
2x
1
dx

du  ln u  ln x 2  4   C
2

x 4
u
6
2x
2


dx

ln
x

4
 ln 40  ln 4  ln 10.
2
0
x 4
Belirli integralde değişken değiştirme. Son örneğimizde belirli integrali hesaplarken, ters
türevin, yani belirsiz integralin belirlenmesinde değişken değiştirme yöntemini kullandık. Bu
yöntemi doğrudan doğruya belirli integral üzerinde de uygulayabiliriz. Hatta bu durumda
zaman kazanılacağı da söylenebilir.
b
 F '(g(x))g'(x)dx 

a
g (b)
g (a )
F '(u) du  F (u) g(a)  F (g(b))  F (g(a))
g (b)
u = g(x) , du = g´(x) dx
x = a  u = g(a) ; x = b  u = g(b)
Son örneğimizi bu yolla yapalım:
2x
0 x 2  4 dx 
6

40
4
1
40
du  ln u 4  ln 40  ln 4  ln 10.
u
u = x2 + 4 , du = 2x dx
x = 0  u = 4 ; x = 6  u = 40
Başka bir örnek:
4
1
3
2
1
x 3x  1 dx  1 u du  1  u3
0
6
6

2
4
2
1
 u
9
3 4
2
1
7


 8 1  .
9
9
1
1
u = 3x2 + 1 , du = 6x dx , x dx = (1/6) du
x=0  u=1 ; x=1  u=4
Başka bir örnek:
 e
1
0
3x
 3x e 3 x  1dx
e 3
1
3
3
2 e 3
1
1 u
u du  
3 2
3
1
e 3 3
1
2
1
1
  u2  e 3  3  .
6
6
6
1
u = e3x – 3x , du = (3e3x – 3) dx , (e3x – 1) dx = (1/3) du
x=0  u=1 ;
x = 1  u = e3 - 3
Uygulama. Haftada x televizyon ünitesi üreten bir işletmenin haftalık marjinal kârı
K´(x) = 165 - (0.1)x , 0  x  4000
olarak veriliyor. Şu anda haftada 1500 ünite üreten firma, haftalık üretimini artırmak
istiyor. Haftalık üretimini 1600 e çıkarırsa, haftalık kârındaki değişim ne olacaktır? Para
birimi TL olsun.
Çözüm. Kârdaki artış
1600
K (1600)  K (1500)  K (x) 1500  1500 K '(x) dx
1600

165  0.1x  dx  165x  0.05x 2
1500
1500

1600
1600
 165  1 600  0.05  2 560 000  165  1 500  0.05  2 250 000
 16500  0.05  31 000  16500  15 500  1000
TL olur.
Daha önce belirsiz integral hesabında kullandığımız kısmî integrasyon yöntemini belirli
integral hesaplarken de kullanabiliriz.

Örnek.
1
0
u=x
,
du = dx



x e x dx  u dv  uv  vdu  xe x  e x dx
dv =
ex
 xe  e
x
dx
x 1
0
 0   1  1.
, v = ex
Bazı integrallerin hesabında değişken değiştirme ve kısmî integrasyon yöntemleri birlik-te
kullanılabilir.
Örnek.
2
1
1 1 2
2
1 


x
ln
x

1
dx



ln
t
dt



ln
t
dt



t
ln
t

t



 dt 
0
1  2  2 1

2
t  
1
2
t = x2 + 1
, dt = 2x dx , x dx = (1/2) dt
x=0 t=1 , x=1t=2
u = ln t
, dv = dt
du = (1/t) dt , v = t
1
1
 t ln t   t   2ln 2  2  0  1
2
2
1
1
1


 2ln 2  1  ln2  .
2
2
Örnek.
1
e
0
t  x , dt 
x
dx 
1
t
x
x 1
2
te
dt
 2 te dt  xe  e 0  0   1  1.
0
t
1
0
1
dx , dx  2 x dt  2tdt
2 x
x  0t  0 , x 1t 1
İntegral için ortalama değer teoremi. f fonksiyonu [a , b] kapalı aralığında sürekli ise,
öyle bir c (a , b) vardır ki
y
b
 f (x)dx  (b  a) f (c)
a
dir.
(c , f(c))
b
1
f (c) 
f (x) dx

a
(b  a)
a
c
f fonksiyonunun [a , b] aralığı üzerinde ortalama değeri
(Average value of f on the interval [a , b] )
Örnek. f(x) = x2 - 3x + 4 ün [-1 , 1] aralığı üzerinde ortalama değeri
1
2
1
1 x3 3 2
2
f (c) 
(x  3x  4) dx  (  x  4 x)


1
(1  (1))
2 3 2
1
11 3
1 3
 11
    4  (   4)   .
23 2
3 2
 3
b
x
Örnek. Fiyat–talep fonksiyonu p  500e ( 0.01) x olarak verilmişse, [200,300] talep aralığı
üzerinde ortalama fiyatın ne olduğunu belirleyelim. Para birimi TL olsun.
Verilen aralıktaki ortalama fiyat p
ile gösterilirse,
300
300
1
500 300 (0.01) x
( 0.01) x
( 0.01) x
p
500
e
dx

e
dx

5
e
dx



200
200
200
(300  200)
100
( 0.01) x 300
e
5
 0.01
  500e
( 0.01) x 300
200
 500(e 3  e 2 )  42.77 TL.
200
Alan Hesabı. Bir eğri ile x - ekseni arasında kalan alan.
y
y = f(x)
b
A   f (x) dx
a
A
a
b
f(x)  0
x
, x  [a , b]
y
a
b
x
A
y = f(x)
f(x)  0
, x  [a , b]
b
A    f (x) dx
a
Alan Hesabı. Bir eğri ile x-ekseni arasında kalan alan.
y
y = f(x)
a
b
c
x
d
Boyalı Alan : A
b
c
d
a
b
c
A   f (x) dx   f (x) dx   f (x) dx
Örnek. f(x) = 3 + 2x – x2 ,
0 x2
ile verilen bölgenin alanı.
y
y = 3+2x – x2
A   3  2 x  x 2  dx  3x  x 2 
2
0
x
3
A
23 
13 
2
 3  2  2    3  1  1  
3 
3
2
0
2
x
7 11
6  .
3 3
3 2
0
Örnek. f(x) = x2 - 2x - 5 ,
0 x 3
ile verilen bölgenin alanı.
y
A    x 2  2 x  5 dx
3
0
1
3
0
x
3
x

2
    x  5x 
 3
0
3
A
y = x2 – 2x - 5
 27

   9  15   0   15.
 3

Örnek. f(x) = x2 - 2x ,
-1  x  1
y
ile verilen bölgenin alanı.
A   x  2 x  dx   x 2  2 x  dx
0
1
2
1
0
y = x2 – 2x
3
1
 1   1  
 0
 1     1  0 
 3
  3  
1
-1
0
x
x
2
2
   x     x 
 3
 1  3
0
3
x
1
1
  1   1  2.
3
3
Örnek. f(x) = xex
,
-1  x  1
ile verilen bölgenin alanı.
y
0
1
A    xe dx   xe x dx
x
1
0
y = xex
  (x  1)e
x 0
1
 (x  1)e
x 1
0
  1  2e 1   0  (1)
1
-1
x
2
2 .
e
Örnek. f (x) 
2x
,
2
x 4
-2  x  2 ile verilen bölgenin alanı.
f (x) 
y
2x
x2  4
–2
x
2
2 2x
2x
A   2
dx   2
dx
2 x  4
0 x 4
0
 ln( x  4)
2
0
2
 ln( x  4)
2
2
0
 (ln 4  ln 8)  (ln 8  ln 4)
 2ln2  ln 4.
İki Eğri Arasında Kalan Alan. f ve g , [a , b ] aralığında sürekli fonksiyonlar, her x  [a , b ]
için g(x)  f(x) olsun . Bu durumda y = f(x) in grafiği y = g(x) in grafiğinin yukarısındadır ve
[a , b ] aralığı üzerinde bu iki eğri arasında kalan alan integral olarak şöyle ifade edilir:
y = f(x)
y
A
A    f (x)  g(x) dx
b
a
y = g(x)
a
b
x
Örnek. f(x) = x + 2 , g(x) = -x2 + 1 , 0  x  2
y
y=x+2
ile verilen bölgenin alanı.
A   x  2   x
2
0
2
 1 dx
  x 2  x  1 dx
A
2
0
1 2
y = -x2 + 1
x
2
x

x
    x 
 3 2
0
3
2
8
20
 22  .
3
3
İki eğri arasında kalan alan hesaplanırken, y = f(x) in grafiğinin bir kısmı y = g(x) in
grafiğinin yukarısında, bir kısmı da aşağısında olabilir. Bu durumda söz konusu aralık alt
aralıklara bölünerek alan hesaplanır. Örnek olarak aşağıdaki şekilde gösterilen bölgenin
alanına bakalım.
y = f(x)
y
a
c
b
x
A : Boyalı alan
y = g(x)
A    f (x)  g(x) dx   g(x)  f (x) dx
c
b
a
c
Örnek. f(x) = -x + 1 , g(x) = x2 - 1 , 0  x  2
A
y
1
0
ile verilen bölgenin alanı.
 x  1  x
2
 1 dx  
   x  x  2 dx  
1
y = x2 - 1
2
0
1
2
1
2
1
x
2
x
2
 1   x  1 dx
 x  2 dx
2
 x
 x

x
x
     2 x      2 x 
 3 2
0  3 2
1
3
2
3
2
 1 1
 8
 1 1 
     2  0    2  4     2
 3 2
 3
 3 2 
 3.
1
y = -x + 1
2
x
Hacim Hesabı , Dönel Cisimlerin Hacmi. Düzlemde bir bölgenin x-ekseni etrafında döndürülmesiyle meydana gelen cismin hacmi integral yardımıyla hesaplanabilir.
y = f(x)
y
Cismin Hacmi : V
f(x)
a
dx
V    f (x)2 dx
b
b
Silindirin Hacmi : dV
dV    f (x)2 dx
x
a
Örnek. f(x) = x2 , 0  x  1 ile verilen bölgeyi x - ekseni etrafında döndürünce meydana
gelen cismin hacmini hesaplayalım.
y
y=
V   x
1
x2

2 2
0
dx
1
   x 4 dx
0
5 1
1
x
x

5
0

 .
5
Örnek(Kürenin hacmi). Yarıçapı r birim olan küre, yarıçapı r birim olan bir yarım çemberin
çapı etrafında döndürülmesiyle elde edilir. Dolayısıyla, sözü edilen hacim
f(x) = (r2 - x2 )1/2 , -r  x  r
eğrisinin x - ekseni etrafında döndürülmesiyle elde edilir.
y
y  r 2  x2
V  
r
r
r

r
r
r
2
2
x
 dx
2
2
 x 2  dx
r
x
-r
r
 2
x3 
   r x  
3  r

 3 r3  3 r3 
  r     r   
3 
3 

4 r 3

.
3
Örnek(Koninin hacmi). Taban yarıçapı r birim ve yüksekliği h birim olan koni,
f(x) = (r/h)x , 0  x  h
eğrisinin x - ekseni etrafında döndürülmesiyle elde edilir.
V   (r / h)x 2 dx
h
y
0
y  (r / h)x

h
0
 r2 2 
 2 x  dx
h

h
x
h
r x 
   2 
h 3 0
 r 2 h3 
  2  
h 3 
 2
 r h.
3
2
3
Rant. Pazarda, bir üründen yüksek fiyatla daha az müşteriye satılarak veya düşük fiyatla daha
çok satın alınarak sağlanan faydaya toplam rant denir.
Kimi üretici ürününü pazar denge fiyatının altında bir fiyata satmaya razı iken pazarda oluşan
daha yüksek fiyattan satabilerek daha çok kazanç sağlamış olur. Üretici lehine oluşan bu
kazanç, üretici rantı olarak bilinir.
Kimi tüketici de pazardaki bir ürünü pazar denge fiyatından daha yüksek fiyata satın almaya
razı iken pazarda oluşan daha düşük fiyattan satın alabilerek bir tür kazanç sağlamış olur.
Tüketici lehine oluşan bu kazanç da tüketici rantı olarak bilinir.
Belli bir piyasada fiyat–arz fonksiyonu p = A(x), fiyat–talep fonksiyonu p = T(x), pazar denge
fiyatı p0 TL ve bu denge fiyatına karşılık gelen ürün miktarı x0 birim ise, bu piyasadaki üretici
ve tüketicilerin sağlayabilecekleri toplam rant aşağıdaki şekil yardımıyla açıklanacaktır.
p
T(0)
(x,T(x))
x0
Rt   (T (x)  p0 )dx
(x,p0)
TÜKETİCİ RANTI
0
p=A(x))
p0
ÜRETİCİ RANTI
p=T(x))
(x,A(x))
A(0)
x
x0
x0
x
Rü   (p0  A(x))dx
0
Örnek. Bir piyasanın fiyat–arz fonksiyonu p(x) = 4x + x2 ve fiyat–talep fonksiyonu
p(x) = 1200 - 72x - x2; para birimi TL dir. Bu piyasanın
a) pazar denge fiyatını
b) toplam üretici rantını
c) toplam tüketici rantını
bulalım.
a) Arz ve talebin çakıştığı ürün miktarı
1200  72 x  x 2  4 x  x 2  2 x 2  76 x  1200  0  2(x 2  38 x  600)  0
 2(x  50)(x  12)  0  x  12
O halde, pazar denge fiyatı
p0  122  4  12  192
TL.
b) toplam üretici rantı
12
12
0
0
Rü   (192  (x 2  4 x))dx   (192  4 x  x 2 )dx
x3
2
 192x  2 x 
3
12
 2304  288  576  1440 TL.
0
c) toplam tüketici rantı
12
12
0
0
Rt   (1200  72 x  x 2  192)dx   (1008  72 x  x 2 )dx
x3
2
 1008 x  36 x 
3
12
 12096  5184  576  6336
0
TL.
Gelir Dağılımı – Lorenz Eğrisi. Bir ülkede milli gelirin ülke bireylerince nasıl bölüşüldü-ğü,
bölüşümün adil olup olmadığının belirlenmesi için uygulanan çeşitli yöntemler vardır. Bu
yöntemlerden biri, nüfusun yüzde kaçının milli gelirin yüzde kaçını aldığının belirlenmesi ve
grafikle gösterilmesidir. Bu şekilde elde edilen grafiğe, yöntemi ilk uygulayan ve geliştiren
Amerikalı istatistikçi Max Otto Lorenz’e atfen Lorenz eğrisi adı verilmiştir.
Lorenz eğrisi şöyle oluşturulur: Ülkedeki bireyler milli gelirden aldıkları pay miktarına göre
(küçükten büyüğe) sıralanırlar. Ülke nüfusu N ise ve 0 ≤ x ≤ N olmak üzere
x
t
N
ise, bu sıralamaya göre ilk x birey nüfusun yüzde 100t lik dilimini oluşturur.
Örneğin, ülke nüfusu 75 milyon ise, ilk 15 milyon kişi, nüfusun yüzde 100(15/75)=20 lik
dilimini oluşturur.
İlk x bireyin gelirleri toplamı g(x), milli gelirin tamamı g(N) = G ise, ilk x bireyin milli,
gelirden aldıkları pay
g(x)
L
G
olmak üzere yüzde 100L olur. Örneğin, yukarıda sözü edilen ülkenin nüfusunun gelir
dağılımına göre ilk yüzde yirmilik dilimini oluşturan 15 milyon kişinin toplam geliri 51 milyar
dolar ve ülkenin milli geliri 850 milyar dolar ise, nüfusun yüzde yirmilik dilimi milli gelirin
yüzde 100(51/850)=6 sını almaktadır.
t
x
g( x )
, L
, 0  t  1, 0  L  1.
N
G
g(Nt ) Lorenz Fonksiyonu.
G
L(t ) 
Lorenz fonksiyonunun tanım kümesi [0,1] aralığı, görüntü kümesi de [0,1] aralığıdır.
y
A
1
y=t
y = L(t)
O
1
B
Lorenz Eğrisi
t
Gelir dağılımının ne dereceye kadar adil olduğunu belirlemek için şu orana bakılır:
1
1
taranan alan 0 (t  L(t ))dt


 2 (t  L(t ))dt.
0
OAB nin alani
1/2
0   1
olduğuna dikkat ediniz.
Gini katsayısı
Örnek. İki ülkede gelir dağılımına ilişkin yapılan çalışmada Lorenz fonksiyonları birinci ülke
için
L1 (t )  (0.93)t 2  (0.07)t
ikinci ülke için
L2 (t )  (0.99)t 2  (0.01)t
olarak elde ediliyor. Hangi ülkede gelir dağılımı daha adildir?
Birinci ve ikinci ülke için Gini katsayıları, sırasıyla
1
 1  2 (t  L1 (t )) dt
0
1
t3 t2
2
 2 ((0.93)t  (0.93)t ) dt  1.86(  )  1.86( 1  1 )  1.86  0.31
0
3 2 0
3 2
6
1
1
3
2
t
t
2
 2  2 (t  L2 (t )) dt  2 ((0.99)t  (0.99)t ) dt  1.98(  )  1.98( 1  1 )  1.98  0.33
0
0
3 2 0
3 2
6
1
1  2
1
Birinci ülkenin gelir dağılımı ikinci ülkenin gelir dağılımına göre daha adil.