Faraday Yasası
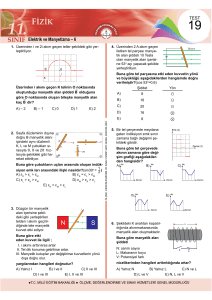
31. Bölüm
1. Faraday İndüksiyon Yasası
Faraday ve Henri:
Değişen manyetik alanlar da emk
(dolayısıyla akım) oluşturur.
Şekilde görüldüğü gibi akım ile
değişen manyetik alan arasında
bir ilişki vardır.
İndüklenmiş emk bir akım
meydana getirmektedir.
Faraday Deneyi
Anahtar aniden açıldığında ya da kapandığında
galvonometre de bir sapma meydana gelmektedir.
Kararlı akımlar durumunda ya da devreden hiç akım
geçmiyorken sapma olmaz.
Faraday İndüksiyon Yasası:
Zamanla değişen manyetik
akı bir emk oluşturur.
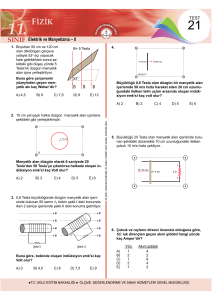
Devre, aynı akımın geçtiği N tane sarımdan oluşursa:
Şekildeki A alanına sahip ilmek B alanı içinde olsun:
B, A ya da θ dan herhangi birinin zamanla
değişimi bir emk yaratır.
Örnek 1
Örnek 2
2. Hareketsel EMK
B alanı zamanla değişirse durgun bir
devrede emk oluşurdu.
Yine B sabitken devre hareket ederse ne olur?
qE
FB
FB nin etkisi ile
+ yükler üste – yükler alt uca toplanır.
Bu iletken içinde bir E alanı oluşturur.
Hareketli bir iletken kapalı bir devrenin
parçası olursa:
Çubuk B alanında hareket ettikçe üzerindeki
serbest yükler indüklenmiş bir akım oluştururlar.
Oluşan manyetik akının zamana göre değişimi
(yani indüklenmiş emk):
Hareketsel emk
İndüksiyon akımı
Çubuk sabit hızla hareket ederse: FB = Fuyg
v
Örnek 4
Örnek 5
3. Lenz Yasası
İndüksiyon emk’nın yönü, manyetik akı değişimine karşı koyacak biçimdedir.
Φ=BA
Sola
Sağa
Dışa doğru bir B alanı yaratır.
İçe doğru bir B alanı yaratır.
Çubuk sağa hareket ettirilirse manyetik akı artar,
O halde indüksiyon akımı bu akıyı azaltacak yönde
manyetik alan yaratmalıdır. Ι saate ters yöndedir.
Ι Saat yönündedir.
Mıknatıs sağa hareket
ettirilirse halkadan geçen akı
artar. Akıda meydana gelen
bu artışa karşı koymak için
indüksiyon akımının yönü
(b) deki gibi olur.
Örnek 6
4. İndüklenmiş EMK ve Elektrik Alanlar
• Değişen manyetik akı,
iletken ilmekte bir emk ve
akım oluşturur.
• Akı değişince iletkende E
alanı da oluşur.
– Bu E alanı elektrostatikteki
E alanının özelliklerinden
farklıdır.
– Ancak indüklenmiş E alanı
korunumlu olmayıp
zamanla değişir.
Bunu incelemek için şekildeki gibi
halka düzlemine dik uygulanan bir
B alanı içindeki r yarıçaplı halkayı
inceleyelim.
B zamanla değişirse emk ve akım oluşur. Bu akım bir E alanı yaratır.
Deneme yükü q halka etrafında 1 kez dolandırmak için
W=qε
kadarlık iş yapmak gerekir.
Ayrıca yüke etkiyen Fe = q E kuvveti de iş yapar.
Değişen B alanı indüklenmiş E
alanı yaratır.
Herhangi bir kapalı yol için emk, çizgi integrali ile bulunur:
Faraday yasasının genel biçimi.
• Buradaki E alanı elektrostatik E alanı
değildir.
• Elektrostatik E alanı korunumlu
olduğundan çizgi integrali sıfırdır.
• Bu nedenle bu E alanına indüklenmiş E
alanı denir. Bu alan korunumlu olmayıp
değişen B alanı ile oluşturulurlar.
Örnek 8
7. Maxwell Denklemleri
Tüm klasik elektromanyetik
etkileşmeler bu
denklemlerle anlaşılır.
Lorentz Kuvveti
1. Denklem: Gauss Yasası
• Kapalı bir yüzeyden geçen akı, yani bu
yüzeyi delerek geçen kuvvet çizgisi sayısı,
yüzeyin içinde hapsedilen net yük miktarı
ile doğru orantılıdır.
• Elektrik alan çizgileri pozitif yüklerden
başlayıp negatif yüklerde sonlanır. Gauss
yasası E alanını yük dağılımına bağlar.
2. Denklem: Manyetizmada Gauss Yasası
• Kapalı bir yüzeyden geçen net manyetik akı
sıfırdır.
• Yani, kapalı bir hacme giren manyetik çizgi
sayısı ile bu hacimden çıkan çizgi sayısı eşittir.
• Bu denklem, manyetik alan çizgilerinin herhangi
bir noktada başlayamayacağını ya da
sonlayamayacağını söyler.
– Bu, o noktada yalıtılmış manyetik tek-kutupun
olmasını gerektirirdi. Ama bu hiç gözlenmemiştir.
3. Denklem: Faraday Yasası
• Herhangi bir kapalı yol boyunca elektrik
alanının çizgi integrali (emk’ya eşittir), bu
kapalı yolun sınırladığı bir yüzeyden geçen
manyetik akının zamanla değişim hızına
eşittir.
4. Denklem: Ampere-Maxwell Denklemi
• Kapalı bir yol boyunca manyetik alanın
çizgi integrali, bu kapalı yol içinden geçen
net akımlar ile bu kapalı yolun sınırladığı
yüzeyden geçen elektrik akısının zamanla
değişiminin toplamına eşittir.