Hatırlatma
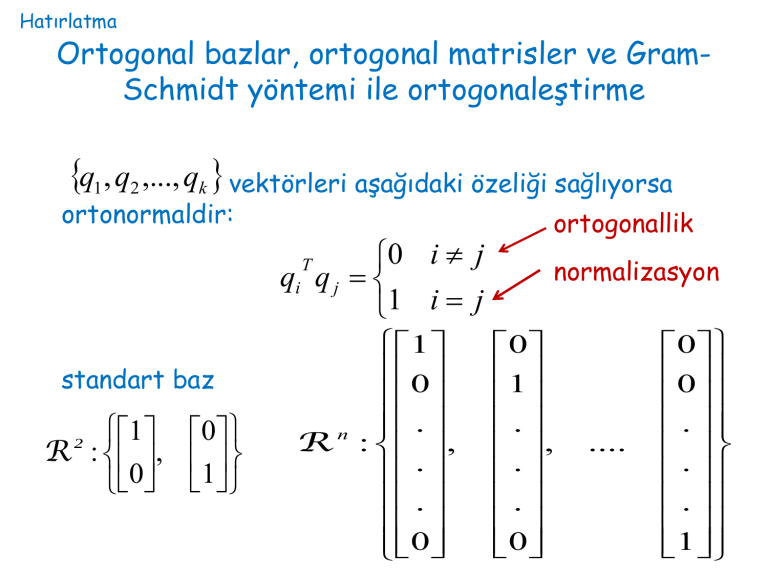
Ortogonal bazlar, ortogonal matrisler ve GramSchmidt yöntemi ile ortogonaleştirme
q1 , q2 ,..., qk vektörleri aşağıdaki özeliği sağlıyorsa
ortonormaldir:
0 i j
qi q j
1 i j
T
standart baz
1 0
R : ,
0 1
2
Rn
1
0
.
: ,
.
.
0
ortogonallik
normalizasyon
0
1
.
,
.
.
0
....
0
0
.
.
.
1
Hatırlatma
*Ortogonal martis, sütunları ortonormal vektörlerden
oluşan kare matristir
*Q’nun sütunları ortonormal vektörlerden oluşmuş ise:
Neden ortogonal
matris denmedi?
QT Q I
q 1T
T
q2
.
T
Q Q q1
.
.
T
qn
q2
1 0 ... 0
0 1 ... 0
. .
... qn
.
.
.
.
0 0 ... 1
QT Q 1
Q dikdörtgen matris olsa bile QTQ=I ancak QT sadece sol
ters
Hatırlatma
Varlık ve teklik teoremi
Varlık: Ax=b’nin her b için en az bir çözümü x vardır
A’nın sütunları Rm ‘i örter
Bu durumda r=m’dir ve ve AC=Imxm sağlayan A’nın nxm
boyutlu sağ tersi vardır.
Bu durum m≤n ise mümkündür.
Hatırlatma
Teklik: Ax=b’nin her b için en çok bir çözümü x vardır
A’nın sütunları lineer bağımsız
Bu durumda r=n’dir ve ve BA=Inxn sağlayan A’nın nxm
boyutlu sol tersi vardır.
Bu durum m≤n ise mümkündür.
Hatırlatma
Sağ ve sol tersleri bulmanın yolu
B ˆ A A
T
Sol ters
1
A
T 1
C ˆ A ( AA )
T
T
Sağ ters
İki örnek
cos
Q
sin
sin
cos
Ortogonal mi?
Başka ortogonal matris hatırlıyor musunuz?
0 1 0
P 0 0 1
1 0 0
Ortogonal matris ile çarpma vektörün boyunu korur
Qx x x
Aynı zamanda iki vektörün iç çarpımı
ve
aralarındaki açıyı da korur
Nasıl anlarız?
Qx T Qy xT QT Qy
xT y
Ortonormal bazın bize sağladığı bir kolaylık…..
q1 , q2 ,...., qn V vektör uzayının ortonormal qi
vektörlerinden oluşmuş bir bazı olsun. v V ise
v 1q1 2 q2 ... n qn şeklinde yazılır
i ‘leri
Ortonormal baz işte burada kolaylık sağlayacak
biliyorsak
v 1q1 2 q2 ... n qn
1
0
0
q1 v 1q1 q1 q q2 ... q qn
T
T
1 q1T v
T
2 1
T
n 1
Ortonormal baz!!!
Benzer şekilde…..
v 1q1 2 q2 ... n qn
0
1
q2T v 1q2T q1 2 q2T q2 ... n q2T qn
.
.
.
0
0
0
2 q2T v
1
qnT v 1qnT q1 2 qnT q2 ... n qnT qn
n qnT v
Tüm bu işlemleri matris şeklinde yazarsak
Sütunları baz vektörleri
baz vektörleri ortonormal olmasaydı
nasıl olacaktı?
Kazancımız matris tersi hesaplamak
yerine…
Q v
T
B v
B v
1
Bir şeye daha dikkat……
aT b
b’nin a’’ya izdüşümü p: p a T
a a
=1
qT v
Tekrar yazalım p
: i qi T , i
q q
n
T
v vektörü için ne diyebiliriz? v q i v qi
i 1
Q mxn boyutunda ise ne olacak….
Artık QT, Q’nun tersi değil ama hala daha QTQ=I
Bunu daha önce
gördük
Sonuç:
Qx bb‘nin çözümü Q kare ise tam çözüm, Q
Ax
dikdörtgen ise en küçük kareler çözümü
Hatırlatma
m denklem ve n bilinmeyen içeren, tutarsız Ax=b denklem
takımının en küçük kareler yaklaşıklığı ile elde edilecek
çözümü x*
ATAx*=ATb
Eşitliğini sağlar ve A’nın sütunları lineer bağımsızsa, ATA
tersinirdir ve
x*=(ATA)-1ATb
b’nin sütun uzayına izdüşümü p de
p=Ax*=A(ATA)-1ATb
eşitliğini sağlar
Q’ nun sütunları ortonormal ise en küçük kareler problemi
basitleşiyor…..
x*=(AT A)-1 ATb yerine x*=(QTQ)-1QTb
ortonormal Q için:
Qx=b (dikdörtgen sistemlerde çoğu b için çözüm yoktur)
QTQx*=QTb (en iyi x* için denklem)
x*= QTb (çözüm)
p=Qx* (b’nin sütunlara izdüşümü- qT bq1 q2T bq2 ... qnT bqn)
1
P=QQT (izdüşüm matrisi)
Gram-Schmidt Yöntemi
Ortonormal vektörler kolaylık sağladığına göre
verilen herhangi bir vektör kümesini ortonormal
vektörlere dönüştürebilir miyiz?
Lineer
özelikleri ne?
bağımsız
v1 , v2 ,...., vn verilmiş olsun, nasıl q1 , q2 ,...., qn ‘ları elde ederiz
Doğrultusu v1 ile aynı,
boyu da 1
v1
Kolay olan q1’i bulmak: q1
v1
q2, q1’e dik olmalı:
Bu neye karşı
düşüyor?
vˆ2 v2 q1 v2 q1 V2’nin q1
Peki, neden
çıkarıyoruz
T
doğrultusunda ki
bileşenine
vˆ2 q1
Ancak ortonormal vektörler kümesine
katılması için boyunun 1 olması gerek
vˆ2
q2
vˆ2
q1,q2 var q3’ü oluşturalım: vˆ3 v3 q1T v3 q1 q2T v3 q2
vˆ3 q1 , vˆ3 q2
vˆ3
q3
vˆ3
Diklik sağlandı birim
olma da sağlanmalı
Benzer şekilde…..
vˆn vn q v q1 q v q2 ... q v qn 1
T
1 n
T
2 n
T
n 1 n
vˆn
qn
vˆn
Eskisi
neydi?
Gram-Schmidt bize A matrisi için yeni bir ayrıştırma veriyor
v1
v2 ... vn q1
A QR
q2
q1T v1
0
.
... qn
.
.
0
q1T v2 ... q1T vn
q2T v2 ... q2T vn
.
.
.
T
0
... qn vn
A sütunları lineer bağımsız mxn boyutunda bir
matris olsun; Q sütunları ortonormal bir matris
ve R tersinir, üst üçgen olmak üzere A’nın
A=QR ayrışımı vardır. m=n ise ve tüm matrisler
kare ise Q ortogonal matristir.
Bu ayrışımı en küçük kareler yönteminde kullanırsak:
(ATA)x*=ATb
(RTQT QR)x*= (RTQT)b
(RTR)x*= (RTQT)b
Rx*= QTb
Biraz tekrar
3 1
0
A 4 2 , b 20
0 2
10
1
1
11
1 1
x1
, x2
21
6 3
1
5
A matrisinin sütunlarından Gram-
Schmidt yöntemiyle ortonormal bir
baz elde ediniz. A=QR ayrışımını elde
edniz ve Ax=b’nin en küçük kareler
çözümünü belirleyiniz.
x1 ve x2 R4 ‘de ortonormal bir küme
oluşturmaktadır. Bu kümeyi ortonormal
baza tamamlayınız.