KAREKÖK ALMA # 6

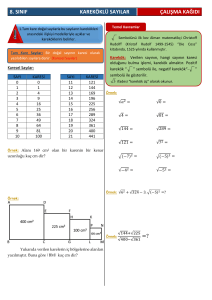
KAREKÖK ALMA
Kuvvet alma
Karekök alma
22 = 2. 2 = 4
4  22  2
52 = 5 . 5 = 25
25  52  5
92 = 9 . 9 = 81
81  9 2  9
...
...
O halde pozitif reel sayılarda karekök alma işlemi , kuvvet alma işleminin tam
tersidir.
Not : Negatif
sayıların
reel
kökü
yoktur.
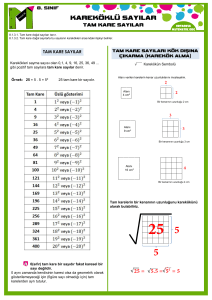
Tam Kare
Kare kökü tamsayı olan sayılara tam kare denir.
ÖR: 1 , 4 , 9 , 16 , 25 , 36 , 49 , . . . , 100 , 121 , 144 . . .
Örnek: 144 sayısının karekökünü bulalım.
144 = 24.32 = 22.3= 4.3= 12
Not :. Karekök alma işlemi verilen sayının hangi sayının karesi olduğunu bulma
işlemidir.
Karekök içindeki bir sayıyı a. b şeklinde yazma
32 sayısını kök dışına çıkaralım.
32 = 16.2 = 16 . 2 = 4. 2
Genel olarak a 2..b = a. b dir.
Karekök içindeki sayı , çarpanlarından birisi bir doğal sayının karesi olacak
şekilde iki sayının çarpımı şeklinde yazılır. Tam kare olan çarpan kök dışına
çıkarılarak köklü sayıya kat sayı yapılır.
Kareköklü Bir Sayının Kat Sayısını Kök İçine Alma
Örnek: 2 5 =
225  4.5  20
Kat sayının karesi alınarak kök içndeki sayının yanına çarpım olarak yazılır. Kök
içindeki sayı ile çarpılır ve çarpım kök içine yazılır.
a b  a 2 .b ‘ dir. (a > 0)
KAREKÖKLÜ SAYILARLA TOPLAMA VE ÇIKARMA İŞLEMİ
Örnek:
3.
3
+5
3
-7
3
=
3 3  5  7 = 3
Kök içleri ayni olan kareköklü sayıları toplayıp veya çıkarırken ; kat sayıları
toplanır veya çıkarılır, ortak kareköke katsayı olarak yazılır.
DEĞERLENDİRME:
1- 2 2 -3 2 +12 2 =?
2- 48 sayısını kök dışına çıkarınız.
3. 3 5 sayısının kat sayısını kök içine alınız.
Kareköklü Sayılarla dört işlem # 7
Kök İçleri Aynı Yapılabilecek Şekilde Verilen Kareköklü Sayılarla Toplama
Çıkarma İşlemi
Örnek:
125  80  20  25.5  16.5  4.5  5 5  4 5  2 5
 5.5  4  2  7 5
Kareköklü Sayılarla Çarpma İşlemi
 Kök içlerinin eşit olması gerekmez.
 Katsayılar çarpılır.


Kök içindeki sayılar aynı kök içine yazılıp çarpılır.
Kök içindeki sayı dışarıya çıkarılabilirse çıkarılır.
Örnekler
2. 2  22  2
5 . 5  52  5
Genel olarak
a . a  a2  a dır. (a>0)
Örnekler
2. 3  6
13. 5  65
Genel Olarak a . b  a.b dir. Bunun tersi de doğrudur. Yani ,
Karekök altında çarpım şeklinde olan sayıların karekökü bu sayıların ayrı ayrı
kareköklerinin çarpımına eşittir.
Kareköklü Sayılarla Bölme İşlemi
a
a
dir. Bunun terside doğrudur.

b
b
Karekök altında bölme şeklinde olan sayıların karekökü , ayrı ayrı kareköklerinin
bölümüne eşittir.
Örnekler
8
1.
2
2.
?
32
2
3.
?
0,01  ?
Alıştırmalar
1. Aşağıda verilen işlemleri yapınız.
a)
c)
6. 24  ? (c=12)
b)
d)
8  18  ?(c  5 2 )
0,25  0,64  1,44  ?(c 
1
)
10
5 6 4  ? ( 7 )
DEĞERLENDİRME Sf. 26-27’ deki alıştirmalar
1. 5 4  2 9  ?(c  16)
2.
64  81  49   ?(c  10)
3. 2 50  128  162  ?(c  9 2 )
4.
46  5  16  ? (c=7)
5.
14  7  1  64  ? (c=4)
6.
7.
-
2 24  3 54
5 27  12
 ? (c=
2. 50  12. 3
2. 32  3. 48
2)
 5 1  ? (c= 1)
0,25  0,81  0,01  ?
Hazırlayan
Mustafa GÜDER