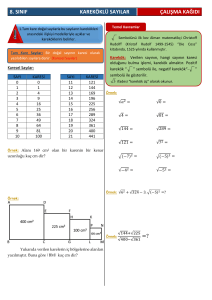
tam kare sayılar ve karekök
Kazanım :Tam kare doğal sayılarla bu sayıların karekökleri
arasındaki ilişkiyi modelleriyle açıklar ve kareköklerini belirler.
Tamkare Sayı : Herhangi bir sayının karesi (ikinci kuvveti)
olan sayılara tam kare sayılar denir.
62 = 36
22 = 4
72 = 49
32 = 9
82 = 64
42 = 16
92 = 81
52 = 25
102 = 100
Karekök içindeki bir sayının kök dışına çıkması için kök
içindeki sayının çarpanları şeklinde yazılması ve bu
çarpanların aynı olması gerekir.Yani tamkare olması
gerekir.
Yukarıda görüldüğü gibi 1, 4, 9, 16, 25, 36, 49, 64, 81 ve
100 sayıları tamkare sayılardır.Çünkü bir sayının karesi
şeklinde ifade edilebiliyorlar.
www.sefahoca.xyz
12 = 1
#Biliyor muyuz?
Örneğin ;
25 52 5
100 102 10
Daha önce tamkare sayıların bazıları öğrenmiştik;
2
1br 1br
1br
2
2br 4br
3br
9br2
4br
3br
2br
16br2
5br
4br
25br2
5br
Siz de alanı 144 br2 olan karenin bir kenar uzunluğu-nu
bulabilir misiniz?
www.sefahoca.xyz
Tamkare sayılar aynı zamanda karenin alanını temsil
etmektedirler.
sembolü ile gösterilir.
Örnek olarak 22 = 4 idi.O halde
32 = 9 idi. O halde
4 = 2 dir.
www.sefahoca.xyz
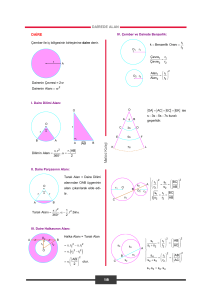
Karekök: Verilen sayının, hangi sayının karesi olduğunu
bulma işlemi karekök almaktır.
Karekök ,
62 = 36
22 = 4
72 = 49
32 = 9
82 = 64
42 = 16
92 = 81
52 = 25
102 = 100
Şimdi de tamkare sayıların kareköklerini bulalım;
Peki alanı 196 br2 olan karenin bir kenar uzunluğunu
bulabilir misiniz?
Basit bir ifadeyle karenin alanından yola çıkarak kenar
uzunluğunu bulmak karekök almaktır.
12 = 1
1=1
36 6
4 =2
49 7
9 =3
64 8
16 = 4
81 9
25 = 5
100 10
9 = 3 dir.
1
web sitemizi ziyaret etmeyi unutmayın...
tam kare sayılar ve karekök
Kazanım :Tam kare doğal sayılarla bu sayıların karekökleri
arasındaki ilişkiyi modelleriyle açıklar ve kareköklerini belirler.
Aşağıda alanları verilmiş karelerin kenar uzunluklarını
bulunuz.
#Biliyor muyuz?
Kök içindeki sayıyı kök dışına çıkarmak için sayıyı
çarpanlarına ayırırsak daha kolay bulabiliriz;
B
C
2
2
2
2
3
3
çarpanları ikişer ikişer gruplandırıyoruz.
144 = 22.22.32 o halde
144 22.22.32 = 2.2.3 =12 olarak bulunur.
A
225 cm2
2
E
cm
144
72
36
18
9
3
1
144 sayısını ;
81 cm2
1
Örneğin
www.sefahoca.xyz
64 cm2
D
49 cm2
H
100 cm2
G
2
16
cm
F
324 cm2
I
örnek:
196 cm2
256
128
64
32
16
8
4
2
1
2
2
2
2
2
2
2
2
çarpanları ikişer ikişer gruplandırıyoruz.
256 22.22.22.22 2.2.2.2 16
şeklinde bulunur.
www.sefahoca.xyz
256 nin değerini bulalmı;
örnek:
169 ve 196 nin değerlerini bulabilir misiniz? Sıra sizde
www.sefahoca.xyz
...
2
web sitemizi ziyaret etmeyi unutmayın...