Bazı Lineer 2-kapılı Direnç Elemanları Akım Kontrollü

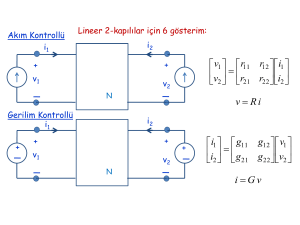
Bazı Lineer 2-kapılı Direnç Elemanları
Akım Kontrollü Gerilim Kaynağı
i2
i1
+
v1=0
_
+
_
+
rmi1
v2
_
 v1   0
v   r
 2  m
0  i1 
0 i2 
 i1   0
i    g
 2  m
0  v1 
0 v2 
Gerilim Kontrollü Akım Kaynağı
i2
i1=0
+
v1
_
gmv1
+
v2
_
Akım Kontrollü Akım Kaynağı
i2
i1
+
αi1
v1=0
+
v2
_
_
v1   0 0  i1 
i    0 v 
 2 
 2 
Gerilim Kontrollü Gerilim Kaynağı
i2
i1=0
+
v1
_
+
_
µv1
+
v2
_
 i1   0 0 v1 
v    0 i 
 2 
 2 
İdeal Transformatör
v1   0 n  i1 
i    n 0 v 
 2 
 2 
n:1
p(t )  v1(t )i1(t )  v2 (t )i2 (t )
1
 v1 (t )i1 (t )  v1 (t )ni1 (t )
n
0
http://www.ece.uci.edu/docs/hspice/hspice_2001_2-2497.jpg
Jiratör
i1
+
v1=0
_
g
i2
+
v2
_
 i1   0 G   v1 
i    G 0  v 
 2 
 2 
Şekildeki 2-kapılının tanım bağıntısını belirleyiniz
L.O. Chua, C.A. Desoer, S.E. Kuh. “Linear and Nonlinear Circuits”, Mc.Graw Hill, 1987, New York
1
+
+
_
V12
İ1 (t)
İ2 (t)
+
2
iˆ1
1
iˆ2
v̂1
3- uçlu
eleman
3
v̂ 2
2
(b)
İ3 (t)
_
_
3
(a)
Şekil (a) daki 3-uçlu elemanın tanım bağıntısını aşağıda verilmiştir:
v13  2i1  3v23  0
4i1  i2  0
a) Şekil (b)’deki uç grafta işaretlenen akım ve gerilimler cinsinden
3-uçlu elemanın tanım bağıntısını bulunuz.
b) Sadece 2-uçlu dirençler ve bağımlı kaynaklar kullanarak verilen
tanım bağıntısına sahip bir 3-uçlu çiziniz.
Lineer olmayan 2-kapılı Direnç Elemanları
RR  v1, v2 , i1, i2  : f1v1, v2 , i1, i2   0, f2 v1, v2 , i1, i2   0
Lineer dirençler için
f1 v1, v2 , i1, i2   11v1  12v2  13i1  14i2  0
f 2 v1, v2 , i1, i2    21v1   22v2   23i1   24i2  0
Lineer olmayanlar için
1
3
f1 v1, v2 , i1, i2   i1  2i2  (v1  v2 )  2(v2  v1 ) 3  0
bir örnek
f 2 v1, v2 , i1, i2   2i1  i2  2(v1  v2 )  (v2  v1 )
3
1
3
0
6 gösterim lineer olmayanlar için nasıl belirlenir
Akım kontrollü
v1  vˆ1 (i1, i2 )
v2  vˆ2 (i1, i2 )
L.O. Chua, C.A. Desoer, S.E. Kuh. “Linear and Nonlinear Circuits”
Mc.Graw Hill, 1987, New York
Gerilim kontrollü
i1  iˆ1 (v1 , v2 )
i2  iˆ2 (v1 , v2 )
Hibrit1
v1  vˆ1 (i1, v2 )
i2  iˆ2 (i1, v2 )
L.O. Chua, C.A. Desoer, S.E. Kuh. “Linear and Nonlinear Circuits” Mc.Graw Hill, 1987, New York
Hibrit2
i1  iˆ1 (v1, i2 )
v2  vˆ2 (v1, i2 )
Transmisyon 1
Transmisyon 2
L.O. Chua, C.A. Desoer, S.E. Kuh. “Linear and Nonlinear Circuits” Mc.Graw Hill, 1987, New York
npn Bipolar Tranzistör
Emitör
Alçak Frekanslardaki Eşdeğeri
Ebers-Moll
Denklemleri
Kollektör
Baz
ie   I ES e

veb
1
vT
ic   F I ES e

  R I CS e
veb
1
vT
 I CS e


vcb
1
vT
vcb
1
vT
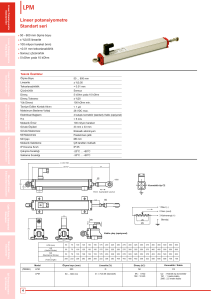
Parametreler: I ES , I CS ,  F , R ,VT
I ES , ICS 1012 1010 A,  F  0.99,  R 0.5  0.8, VT ~
 25mV (25 C)
Ebers-Moll Denklemleri ile verilen tranzistör nasıl bir eleman?
3-uçlu, gerilim kontrollü
L.O. Chua, C.A. Desoer, S.E. Kuh. “Linear and Nonlinear Circuits” Mc.Graw Hill, 1987, New York
3-uçlu elemanın referansını baz yerine emitör olarak alırsak...
vbe  veb
vce  vcb  veb
ib  (ie  ic )
ib  (1   F ) I ES e
ic   F I ES e
vb e
1
vT
vb e
1
vT
Ebers-Moll
denklemlerine
yerleştir
 (1   R ) I CS e
 I CS e
vb e vce
1
vT
vb e vce
1
vT
L.O. Chua, C.A. Desoer, S.E. Kuh. “Linear and Nonlinear Circuits” Mc.Graw Hill, 1987, New York
L.O. Chua, C.A. Desoer, S.E. Kuh. “Linear and Nonlinear Circuits” Mc.Graw Hill, 1987, New York
Ortak emitör karakteristiklerinin parça parça lineer eşdeğeri
Biraz daha basitleştirirsek....
L.O. Chua, C.A. Desoer, S.E. Kuh. “Linear and Nonlinear Circuits” Mc.Graw Hill, 1987, New York
DC Çalışma Noktasının Belirlenmesi
D1
D2
KGY+ KAY+ETB
vbe  E1  R1ib vce  E2  R2ic
Varsayım: E1  0, E2  0
D1 kısa devre, D2 açık devre
vbe  E0
ib 
ic  ib
vce
ic 
1
( E1  E0 )
R1

( E1  E0 )
R1
R2
 E2  
( E1  E0 )
R1
L.O. Chua, C.A. Desoer, S.E. Kuh. “Linear and Nonlinear Circuits” Mc.Graw Hill, 1987, New York
VbeQ  E0 , I bQ
E1  E0

,
R1
VceQ  E2  
R2

( E1  E0 ), I cQ 
( E1  E0 )
R1
R1