Ural Federe Bölgesi Öğretmen Evi X. Uluslararası Bilim Temelleri

Ural Federe Bölgesi Öğretmen Evi
X. Uluslararası Bilim Temelleri Bilgi Yarışması
2013-2014 öğretim yılı
1.etap
Matematik
11.sınıf
Andrew John Wiles‘e ithafen
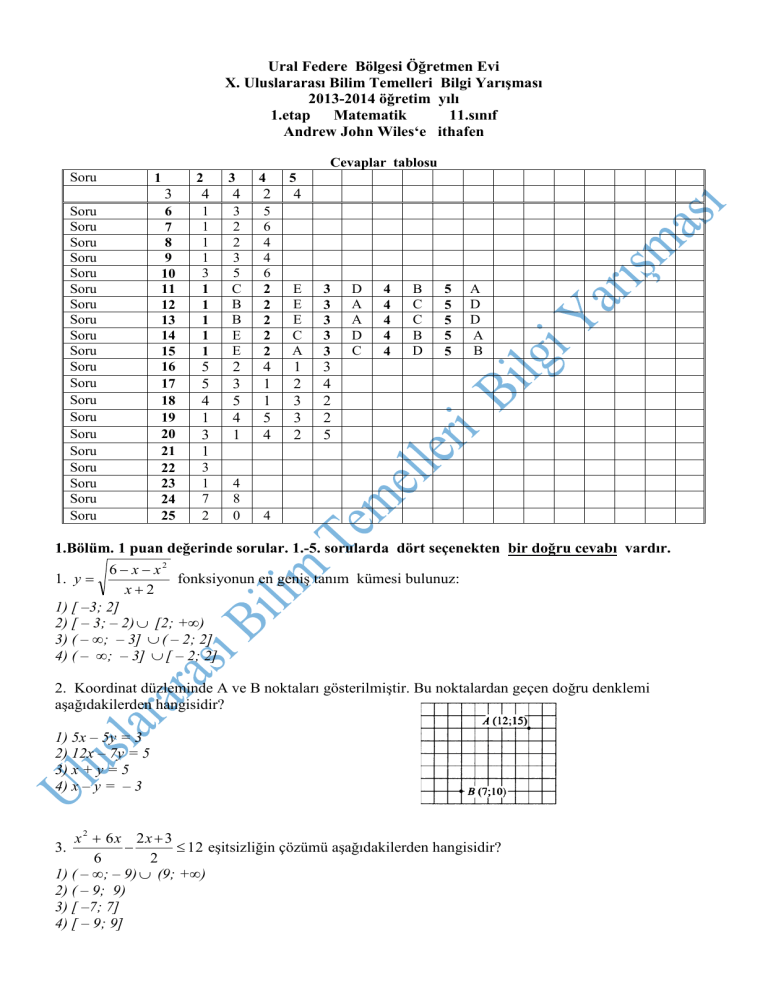
Cevaplar tablosu
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
1
2
3
4
5
3
4
4
2
4
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
1
1
1
1
3
1
1
1
1
1
3
2
2
3
5
C
В
B
E
E
5
6
4
4
6
2
2
2
2
2
E
Е
E
C
A
3
3
3
3
3
5
5
4
1
3
1
2
3
5
4
1
4
1
1
5
4
1
2
3
3
2
3
4
2
2
5
4
8
0
4
3
1
7
2
D
A
A
D
C
4
4
4
4
4
B
С
C
B
D
5
5
5
5
5
A
D
D
A
B
1.Bölüm. 1 puan değerinde sorular. 1.-5. sorularda dört seçenekten bir doğru cevabı vardır.
6  х  х2
fonksiyonun en geniş tanım kümesi bulunuz:
х2
1) [ –3; 2]
2) [ – 3; – 2)  [2; +∞)
3) ( – ∞; – 3]  ( – 2; 2]
4) ( – ∞; – 3]  [ – 2; 2]
1. у 
2. Koordinat düzleminde A ve B noktaları gösterilmiştir. Bu noktalardan geçen doğru denklemi
aşağıdakilerden hangisidir?
1) 5х – 5у = 3
2) 12х – 7у = 5
3) х + у = 5
4) х – у = – 3
х 2  6х 2х  3

 12 eşitsizliğin çözümü aşağıdakilerden hangisidir?
6
2
1) ( – ∞; – 9)  (9; +∞)
2) ( – 9; 9)
3) [ –7; 7]
4) [ – 9; 9]
3.
4. у = х2(1 – 2х) fonksiyonun türevini bulunuz:
1) у '  x  4x 2
2) y '  2 x  6 x 2
3) y '  2 x  6 x 2
4) y '  4 x  6 x 2
5. cos
6
7
6
7
 cos
 sin
 sin
çarpımının sonucu aşağıdakilerden hangisidir?
5
10
5
10
1) 1

10

3)  sin
10
4) 0
2) cos
2.Bölüm. 3 puan değerinde sorular. 6.-10. sorularda altı seçenekten üç doğru cevabı vardır.
6. Aşağıda verilen ifadelerden doğru eşitlikleri seçiniz:
1) sin 2   cos2   1
2) sin     sin cos   cos sin 
3) cos(   )  cos cos   sin  sin 
4) cos(   )  cos cos   sin  sin 
5) sin     sin cos   cos sin 
6) sin 2   cos2   1
7. АВСD üçgen piramitin BC kenarı, ABD üçgen düzlemine diktir, BC = │12│’dir. ABD üçgenin
m( ABD)  900 , m( DAB)  300 ,│ АD│ = 14'tür. Buna göre aşağıdakilerden doğru ifadeleri seçiniz.
1) ВСD ve ABD düzlemleri dik kesişendir.
2) D noktasının ABC düzlemine uzaklığı 7’dir.
3) A noktası ve CD doğrusu arasındaki uzaklık 14’dür.
4) АВD ve СВD düzlemleri arasında açının tanjantı 0’dir.
5) A noktası ve [BD] doğru parçası arasındaki uzaklık 7’dir.
6) A noktası ve [BC] doğru parçası arasındaki uzaklık 7 3 ’tür.
8. М ve N, АВСDA1 B1C1 D1 paralel yüzlüsününün СС1 ve ВС ayrıtlarının ortasında bulunan noktaları
olduğuna göre aşağıdaki ifadelerden doğru olanları seçiniz:
1) [BC] ve [A1D1] eş doğru parçalarıdır.
2) [MN] ve [AD1] lineer bağımlıdır.
3) [BC1] ve [CB1] dik kesişirler.
4)[ NM] ve [BC] doğrudaştır.
5) NM   2 ВС1
6) [AA1] ve [D1D] lineer bağımlıdır.
9. Doğru ifadeleri seçiniz:
1) sin    cos 
'
2) cos '  sin
3) cos 3  = – 3sin(3  )
'
4) ((2 – 3х)2)’= – 12 + 18x
5) u n   u n 1
6) ((2 + 3х)2)’= 4 + 6x
'
10. Doğru ifadeleri seçiniz:
1) İki düzlem bir doğruyu dik keserse, bu düzlemler birbirine diktir.
2) Aynı doğrultuda olmayan en az bir nokta bir düzlem belirtir.
3) Küpün bütün ayrıtları birbirine diktir.
4) Prizmanın tabanı kare ise bu dik prizmadır.
5) Dikdörtgenler prizmasının yanal alanı, taban çevresinin uzunluğu ile yan ayrıtının çarpımına eşittir.
6) Dik prizmalarda taban şekli ne olursa olsun, hacim, taban alanı ile yüksekliğin çarpımıdır
3.Bölüm. 5 puan değerinde sorular. 11.-15.sorularda eşleştirme, 16.-20.sorularda sıralama yapılacaktır.
Cevap,her kare içine bir harf veya rakam olarak yazılacaktır ( Örnek 1A2B3C4D5E, ABCED, 12435 ). Büyük
harf ve kitap harfi (el yazısı değil ) kullanınız. Nokta, virgül ve diğer işaretleri kullanmayınız.
11. İfadeleri sadeleştirip uygun eşleştirmeleri yapınız:
İfadeler
1) sin t  cost  tgt
2) sin t  cost  ctgt
3) sin2 t  tgt  ctgt
sin 2t
 sin t
4)
cos t
5) cos2 t  sin2 t  (ctg 2t  1)
Sonuç
А)  sin t
В) sin t
2
С) sin 2 t
D)  cos2 t
Е) cos2 t
14. Bu bilgi yarışması; İngiliz ve Amerikan matematikçi Andrew John Wiles’e ithaf edilmiştir. Andrew John Wiles ile
ilgili verilen ifadeleri tamamlayınız:
Açıklamalar
1) Andrew John Wiles, ….. yılında Cole Ödülü almıştır.
2) Andrew John Wiles, ….. yılında Wolfskehl Ödülü almıştır.
3) Andrew John Wiles,…. yılında Fermat'ın Son Teoremi profesyonel
çalışması başlamıştır.
4) Andrew John Wiles, ….. yılında Kral Faysal Ödülü almıştır.
5) Andrew John Wiles, ….. yılında Britanya İmparatorluğu Şövalyesi
olmuştur.
13. ( – 7 ; 7) aralığında у = f(х) türev fonksiyonun grafiği
şekilde gösterilmiştir. Buna göre doğru ifadeleri eşleştiriniz
Tarih
A)1986
B) 1996
C) 1998
D) 2000
E) 1997
Açıklamalar
1) [– 6; 6] aralığında fonksiyonun extremum noktaların sayısı …
2) у = f(х)fonksiyonun artan aralıkların sayısı …
3) Azalma aralığın en büyük uzunluğu …..
4) Fonksiyonun minimum nokta sayısı …
5) [– 6; 0] х0= aralığında fonksiyonun extremum noktası …
14. Formülleri ile grafikleri eşleştiriniz:
Sonuç
А) 6
B) 3
C) 1
D) – 4
E) 2
Formül
1) у  log 1 x
Grafik
А)
2
х
1
2) у =   – 3
2
B)
3) у  log2 ( x  2)
C)
4) у = 2х – 1
D)
5) у = х – 2
E)
15. Problemleri çözüp uygun eşleştirmeleri yapınız:
Açıklamalar
1) Bir zar bir defa atıldığında üst yüzüne çift sayı gelme olasılığı
kaçtır?
2) Bir zar bir defa atıldığında üst yüzüne 3 sayı gelme olasılığı
kaçtır? (sayıyı en yakın yüzlüğe yuvarlayınız)
3) Aynı anda bir çift zar atıldığında üst yüze gelen sayıların
toplamının 8 olma olasılığı kaçtır? (sayıyı en yakın yüzlüğe
yuvarlayınız)?
4) Aynı anda bir çift zar atıldığında üst yüze gelen sayıların
toplamının 5 olma olasılığı kaçtır? (sayıyı en yakın yüzlüğe
yuvarlayınız)?
5) Aynı anda iki zar atıldığında her iki zarın üst yüze çift sayı gelme
olasılığı kaçtır?
Cevaplar
A) 0,17
B) 0,25
C) 0,14
D) 0,11
E) 0,5
16. İşlemlerin sonuçları küçükten büyüğe doğru sıralayınız:

 
 
1) sin    cos  cos  
3
 4
 4




2) cos  cos  cos  cos
6
4
3
2
 
 3 
3) sin    cos    sin 

 2
 2 
4) sin

 cos
6
 3
5) sin 
 4

6
 sin

3
cos 0



 
 
  cos    sin  cos  cos 0  sin  
4
2

 4
 2
17. Aşağıdaki sayıları büyükten küçüğe doğru sıralayınız:

1)
2

2)
3
3) 2
4) 3  2
5) 2,5
18. Aşağıdaki sayıları küçükten büyüğe doğru sıralayınız:
1) 2
1
3
2) 21,5
3) 2
2
4) 2
2
5) 1
19. x0 noktasında у  f (x) fonksiyonun değişim oranları bulup büyükten küçüğe doğru sıralayınız:
1) f ( x)  x2 , x0  2
2) f ( x)  2x2 , x0  1
1 2
x , x0  2
2
1
4) f ( x)  , x0  2
x
2
5) f ( x)  , x0  2
x
20. Denklemlerin kökleri bulup küçükten büyüğe doğru sıralayınız:
1) log3 x  1
1
2) log5 x 
2
3) log 1 x  1
3) f ( x) 
7
4) log 5 x  0
5) log1 x  3
2
4.Bölüm. 6 puan değerinde sorular. 21.-25. sorular. Cevap, ilk kareden başlayarak rakam veya kelime (tekil ve
yalın durumda !)her kare içine bir rakam veya bir harf olarak yazılacaktır. Büyük harf ve kitap harfi (el yazısı
değil ) kullanınız. Cevap, iki veya fazla kelimeden ise virgül kullanınız.
Ondalık kesri yazabilmek için virgül işareti kullanınız.
21. arcsin(5  4 x)  arcsin x 2 denkleminin sonucunu bulunuz.
22. х  4 ve х  4  (2х  5)  0 eşitsizlik sistemini sağlayan tamsayıların toplamını bulunuz.
23. Aynı miktarda % 13 lük ve % 15 lik iki çözelti karıştırıldığında yeni karışım % kaçlık olur?
24. Bir araba, ilk saatte 120 km /h, sonraki iki saatte 85 km/ h ve daha sonraki iki saatte 50 km / h hızla
giderse ortalama hızı kaç olur?
25. Bir satranç tahtasında toplam kaç tane ‘kare’ vardır?
Ural Federe Bölgesi Öğretmen Evi
XI. Uluslararası Bilim Temelleri Bilgi Yarışması
2014-2015 eğitim-öğretim yıl 1.etap Matematik
11.sınıf
Cevap Anahtarları
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
1
2
3
4
5
2
4
3
1
4
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
2
1
1
2
1
1
1
1
1
1
4
2
2
4
4
C
В
С
B
D
6
5
5
5
5
2
2
2
2
2
E
Е
A
D
A
3
3
3
3
3
3
4
3
3
3
6
5
1
2
2
4
8
4
2
5
5
2
3
2
5
4
4
1
7
1
3
1
1
5
6
0
7
5
R
2
5
5
E
C
O
R
D
A
B
A
B
4
4
4
4
4
D
E
B
С
E
E
E
5
5
5
5
5
A
D
D
C
C
25.SORU 1.CEVAP RECORDE 2.CEVAP REKORDE 3.CEVAP REKORD.
22.soru a=0 y=2 x =5
Soru
25
1.Bölüm. 1 puan değerinde sorular. 1.-5. sorularda dört seçenekten bir doğru cevabı vardır.
x2  2x  3
 0 eşitsizliğin çözüm kümesi aşağıdakilerden hangisidir?
1. 2
x  x 6
1)  3;2 1;3
2)  3;2  1;3
3)  3;2  1;3
4)  ;3  2;1 3;
2. Şekilde gösterilen grafik aşağıdaki fonksiyonlardan
hangisine aittir?
1)
2)
3)
4)
y  2 sin x
y  2 sin x
y  cos 2 x
y  2 cos x
2
 x
3. cos    
2
 4
3 k

,k  Z
1) 
16
2
4.
1)
37
2
 12 2

eşitliğinin çözüm kümesi hangisidir?
2) (1)k 3  6 k , k  Z
3)  3  8k ,k  Z
4) 3  7 k , k  Z
n
5 2 n 1  7 2 n  1
kesrinin eşiti hangisidir?
7
5
2)
5
7
3)
1
35
4)
25
49
5. Bir yamuğun üst tabanı ile alt tabanı oranı 3/4 ve orta tabanı 28 olduğuna göre en büyük tabanı kaçtır?
1) 24
2) 64
3) 16
4) 32
2.Bölüm. 3 puan değerinde sorular. 6.-10. soruların altı seçenekten üç doğru cevabı vardır.
Cevap, her kare içine rakam olarak virgül kullanılmadan yazılacaktır ( Örnek 123).
6. Aşağıdaki eşitliklerden hangileri doğrudur?
1) cos 2   sin2   1
2tg
2) tg 2 
1  tg 2
3) sin 2  2 sin
4) cos 2  cos 2   sin2 
5) cos 2  1  2 sin2 
6) sin2  2 sin  cos
7. Doğru ifadeleri seçiniz:
1) Karmaşık sayılar kümesi C ile gösterilir.
2) a ve b birer reel sayı ve i  1 olmak üzere, z = a + bi şeklinde ifade edilen z sayına, karmaşık
sayı denir.
3) a ve b tam sayı ve sıfır olmamak üzere a/b şeklindeki sayılara karmaşık sayı denir
4) İrrasyonel sayılar kümesi ile rasyonel sayılar kümesinin birleşimi karmaşık sayılar kümesini oluşturur.
5) Reel kısımları ve imajiner kısımları kendi aralarında eşit olan iki karmaşık sayı,birbirine eşittir.
6) Her tam sayı karmaşık sayıdır ve her karmaşık sayı da tam sayıdır.
8. Doğru ifadeleri seçiniz:
1) Herhangi iki rasyonel sayı arasında sonsuz sayıda rasyonel sayı bulunur.
2) Herhangi iki irrasyonel sayı arasında sonsuz sayıda rasyonel sayı bulunur.
3) Herhangi iki irrasyonel sayının toplamı rasyonel sayıdır.
4) Herhangi iki rasyonel sayının toplamı irrasyonel sayıdır.
5) Herhangi iki rasyonel sayı arasında sonsuz sayıda irrasyonel sayı bulunur.
6) ) Herhangi bir irrasyonel sayı ile rasyonel sayının toplamı tam sayı olabilir.
9. Aşağıdaki eşitliklerden hangileri doğrudur?
5
1

3
2
11  1
2) sin 

 6  2
1) cos
3) cos 3300 
1
2
4) tg( 1800  t )  tgt
5) ctg3150  1
6) cos( 
7
1
)
3
2
10. Doğru ifadeleri seçiniz:
1) Havaya atılan bir tavla zarının 7 gelme olasılığı sıfırdır.
2) Aynı düzlemde 4 farklı çember, en fazla 16 noktada kesişir.
3) Bir kesin olayın olma olasılığı ½’dir.
4) İki zar aynı anda havaya atıldığında üste gelen sayıların toplamını 10 olma olasılığı 1/12’dir.
5) Sevgi,3 etek ve 4 bluzu ile 12 farklı biçimde giyinebilir.(etekleri ve bluzu üst üste giymeden)
6) Hiç bir olayın olma olasiliği 1'den küçük olamaz.
3.Bölüm. 5 puandeğerindesorular. 11.,12.,13.,14.,15. sorularda eşleştirme, 16.,17.,18.,19. ve
20.sorularda sıralama yapılacaktır. Cevabı,her kare içine bir harf veya rakam olacak şekilde yazınız.
( Örnek 1A2B3C4D5E, ABCED, 12435 ). Büyük harf ve kitap harfi (el yazısı değil ) kullanınız. Nokta,
virgül ve diğer işaretleri kullanmayınız.
11. ABCDA1B1C1D1 birim küptür. M noktası [BC] kenarın orta noktası olduğuna göre sol üstte verilen iki
doğru parçası arasındaki açı değerlerini bulunuz:
Doğrular
Açı değeri
1) [AC] ve [BD]
1
А) arctg
2
2)[AA1] ve [B1C]
В) 600
3) [A1C] ve [BB1]
С) 900
4) [AD1] ve [A1B]
D) arctg 2
5) [A1A] ve [B1M]
Е) 450
12. ABCD paralelkenarında köşegenlerin kesiştiği nokta О (0; 1,5; 0) dir. Köşe noktalarından ikisi
A (1; 3; –1), B (–2; 1; 0) olduğuna göre aşağıda istenilen nokta ve kenar koordinatları eşleştiriniz.
Şart
Sonuç
1) C noktasının koordinatları …
A) (–0,5; 2; –0,5)
2) D noktasının koordinatları …
B) (–1; 0; 1)
3) [AB] kenarın orta noktasının koordinatı …..
C) (1,5; 2,5; –0,5)
4) [AD] kenarın orta noktasının koordinatı …..
D) (–3; –2; 1)
E) (2; 2; 0)
5) AB vektörün koordinatları …
13.Yandaki şekilde, (–3; 10) aralığında tanımlı y  f ( x ) fonksiyonun
türevinin grafiği gösterilmiştir. Buna göre doğru ifadeleri eşleştiriniz:
Açıklama
1)[–2; 5]aralığında fonksiyonun ekstremum noktaları sayısı …. tanedir.
2) у = f(х) fonksiyonun artış aralığın uzunluğu … birim kadardır.
3) En büyük azalma aralığın uzunluğu … birim kadardır.
4) [0; 4] aralığında fonksiyonun en büyük türev değeri х = … apsisinde elde edilir.
5) ) [0; 4] aralığında fonksiyonun en küçük türev değeri … dir.
14. Uygun eşleştirmeleri yapınız:
Açıklama
1) Çember çevresinin uzunluğunun, çapının uzunluğuna bölünmesi ile elde
edilen sabit sayı ………….
2) 1 ve kendisinden başka hiçbir sayma sayısı ile bölünemeyen 1’den
büyük tam sayı …………
3) a ve b tam sayı ve sıfır olmamak üzere a/b şeklindeki sayı ……..
4) İki tam sayının birbirine bölümü şeklinde yazılmayan sayı ………
5) Katsayıları tam sayılar olan bir polinomun kökü olarak ifade edilebilen
sayı ……………..
Sonuç
А) 7
B) 6
C) 1
D) 0
E) 3
Matematik terim
A) Rasyonel sayıdır
B) Pi sayısıdır
C) Cebirsel sayıdır
D) Asal sayıdır
E) İrrasyonel sayıdır
15. Şatranç oyununda Şaban’in hile yapma olasılığı 0,6'dır. Kazanma olasılığı 0,1 ve berabere kalma
olasılığı 0,2 dir. Diğer durumlarda kaybediyor. Buna göre aşağıdaki ifadeleri eşleştiriniz.
Açıklama
Olma
olasılığı
1) Rastgele seçilmiş bir oyun partisinde Şaban’ın hile yapması ama yeni de A) 0,12
kazanmaması olasılığı …. dir.
2) Rastgele seçilmiş bir oyun partisinde Şaban’ın hile yapmaması ve oyunu kaybetmeme B) 0,36
olasılığı … dir.
3) Rastgele seçilmiş bir oyun partisinde Şaban’ın hile yapmaması ve oyunu C) 0,42
kazanmaması olasılığı …. dir.
4) Rastgele seçilmiş bir oyun partisinde Şaban’ın hile yapması ve oyunu kaybetmeme D) 0,54
olasılığı … dir.
5) Rastgele seçilmiş bir oyun partisinde Şaban’ın hile yapması ve oyunu kaybetmesi E) 0,18
olasılığı … dir.
16. Temel trigonometrik özdeşlikleri kullanarak istenen trigonometrik fonksiyon değerlerini bulunuz.
Fonksiyonları, değerlerine göre küçükten büyüğe doğru sıralayınız:
3

1
1) arc cos x  ise sin 2 x  ?
2) arcsin x  , 0  x  ise cos x  ? 3) arcctgx  3 ise tan x  ?
3
5
2
3

4
4) arcsin x  , x  (0; ) ise tan x  ?
5) arccosx  ise tg 2 x  ?
5
2
5
17. Aşağıdaki ifadeleri değerlerine göre büyükten küçüğe doğru sıralayınız:

2
1
3

3) arcsin  
4) arccos 
1) arccos 0
2) arcsin

2
2


2


5) arctg1
18. Aşağıdaki fonksiyonların verilen aralığa göre en büyük değerlerini bularak küçükten büyüğe doğru
sıralayınız:
1) y  3  2 x , x   1;3
2) y  2 x 2  2 x , x   3;2
3) y   x , x  1;9
  
5) y  tgx, x   ; 
 4 4
4) y  2 sin2 x , x    ;  
19. Aşağıdaki ifadeleri değerlerine göre büyükten küçüğe doğru sıralayınız:
1) 0 ,3
9
2
3) 0,3
2) 1
4)
1
2
0 ,3
5)
1
3
0 ,3
20.Belirtilen aralıkta her denklemin kökünü bulunuz ve kök değerlerine göre küçükten büyüğe doğru
sıralayınız:
1) sin x 
2
,
2
 
 2 ;  
4) tgx 
2) cos x 
1
,
3
 
0; 2 
2
,
2
  
 6 ; 3 
3) sin x  0, 0,  
5) sin x  1, 0; 2 
4.Bölüm. 6 puandeğerindesorular. 21.-25. sorular. Cevap olacak rakam veya kelime ilk kareden
başlayarak (tekil ve yalın durumda!)her kare içine bir rakam veya bir harf gelecek şekilde
yazılacaktır. Büyük harf ve kitap harfi (el yazısı değil ) kullanınız. Cevap, iki veya daha fazla
kelimeden oluşuyor ise virgül kullanınız. Ondalık kesri yazabilmek için virgül işareti kullanınız.
21. Bir ev çatısının düzgün dörtgen piramit şekli vardır. Çatı yüksekliği 2,4 metre, yan yüz yüksekliği ise 7,4
metredir. Çatıyı kaplamak için, %10 kadar fazla (yedek olsun diye) kiremit alınacaktır. Kiremidin 1m2 si 300
ruble olduğuna göre bu çatıyı kaplamak için kaç rubledir gerekir?
22. x,y ve a rakam ve yx,xa ve ya iki basamaklı sayılar olmak üzere
1) yx + yx = xa
2) yx –yx = a
3) yx – x = ya
olduğuna göre a ,y, x rakamlarını bulunuz.
Cevap tablosuna bulunan rakamları küçükten büyüğe doğru virgül kullanmadan yazınız.
23. Bir sınıfta 30’dan az öğrenci vardır. Seçilen rastgele bir kız öğrencinin başarılı çıkma olasılığı
rastgele bir erkek öğrencinin ise başarılı çıkma olasılığı
3
,
13
4
olduğuna göre bu sınıfta kaç başarılı öğrenci
11
vardır?
24. Baba ile oğlunun yaşların toplamı 38, oğlu ile dedenin yaşların toplamı 64, baba ile dedenin yaşların
toplamı 84 olduğuna göre dedenin yaşı kaçtır? Cevap tablosuna sadece rakam yazınız.
25. 16.yüzyıla kadar bütün matematikçiler kendilerine has “eşittir” işaretleri kullanırlardı ve ortak bir
gösterim biçimi olmaması, birbirlerini anlamalarını zorlaştırmaktaydı. “Eşittir”işaretinin günümüzdekine
benzer şeklini ile ilk kez 1557 yılında İngiliz matematikçi ve doktor, Robert …… kullanmıştır. The
Whetstone of Witte adlı yapıtında şöyle açıklama yapmış : "Eşittir sözcüğünü bıktırıcı bir biçimde tekrar
tekrar kullanmaktansa, genelde çalışırken yaptığım gibi paralel iki çizgi koyacağım, çünkü paralel iki
çizgiden daha eşit bir şey olamaz" diyerek ilk kez kullanmıştır.
Cevap tablosuna matematikçinin soyadı yazınız.
Ural Federe Bölgesi Öğretmen Evi
X. Bilim Temelleri Bilgi Yarışması
PREMİER LİG 2013-2014 öğretim yılı
Matematik
Final
İngiliz matematikçi Andrew John Wiles ‘e ithafen
Cevap anahtarları
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
1
2
3
4
5
6
7
8
9
10
11
12
2
1
1
1
1
1
1
1
4
3
1
1
5
2
2
2
4
E
E
D
1
5
А
D
6
6
4
4
5
2
2
2
2
2
2
2
D
C
E
5
4
D
B
3
3
3
3
1
3
3
C
D
C
4
4
4
B
A
A
C
A
4
4
В
C
Soru
Soru
Soru
Soru
Soru
Soru
Soru
13
14
15.1
15.2
15.3
15.4
16.1
M
7
4
1
4
1
-
İ
3
L
1
E
6
N
5
Y
2
U
8
M
4
0
,
2
5
5
5
5
A
B
B
11.sınıf
Soru
Soru
Soru
16.2
16.3
16.4
3
-
1
1
2
,
7
5
1.Bölüm. 3 puan değerinde sorular. 1.-5. sorularda altı seçenekten üç doğru cevabı vardır.
Doğru yanıtların numaralarını cevap tablosuna yazınız.
1. Aşağıdaki eşitsizliklerden hangileri yanlıştır?
1) sin1cos2sin3cos4 > 0
2) cos1sin2cos3sin4 < 0
4) sin1sin2sin3sin4 < 0
5) sin1sin2cos3cos4 < 0
3) cos1cos2cos3cos4 < 0
6) cos1cos2sin3sin4 < 0
2. (‒2; 0) aralığında türevleri negatif olan fonksiyonlar aşağıdakilerden hangileridir?
1)
2)
3)
4)
5)
6)
3. Aşağıdaki dizilerden hangileri sınırlıdır?
1) y n  3 
5
n
4) y n  5  n 1
3) y n  3n 2  8
2) yn  (1) n sin n
5) y n  5n  8
6) y n 
2n  1
5
4. Köklerin çarpımı pozitif olan denklemler aşağıdakilerden hangileridir?
1) x 2  2 x  3x  6
x2  3
x
 2
 2,5
4)
x
x 3
2) 5
x 3  6  x
5) x 2  3x 
5
3
8
x  3x  2
2
5. Aşağıdaki fonksiyon grafiklerinden hangileri periyodiktir?
x 2
 27
3) 3
2x  5
3
6)
x2
2.Bölüm. 5 puan değerinde sorular. 6.-8.sorularda uygun eşleştirme, 9.-10.sorularda uygun sıralama
yapılacaktır.
Cevap,her kare içine bir harf veya rakam olarak yazılacaktır ( Örnek 6.-8.sorularda 1A2B3C4D5E, 9.-10.sorularda- 13425 ). Büyük harf ve kitap harfi (el yazısı değil ) kullanınız. Nokta,
virgül ve diğer işaretleri kullanmayınız.
6. Denklemler ile uygun kökleri eşleştiriniz:
A) ‒4
1) ( x  2) x  x 2  0
2) x 8  2 x  7 8  2 x  0
B) 5,0625
3) 3x  2 x  8
C) 4
4) 2 x  74 x  3  0
D) 3
E) 0
5) 2 x 2  1  x 2  1
7. Aşağıdaki eşitsizlikleri çözüm kümeleriyle eşleştiriniz.
A) 1,5;2
1) 510 x  5 4  56 x
x 2 10 x 9
B) 2;
1
2) 19
13
3) 7 x
2
0,3
 49 20
x 2 1, 5 x
1
4)  
 7  2 x 3
7
 
5) 2  3 x  1 3 x  9  0
C) 1;9
D) - ;-1  1;
E) 1; 
8. Aşağıda verilen problemleri cevaplarıyla eşleştiriniz.
1) Çevresi104 birim olan eşkenar dörtgenin bir köşegeni 48 birim olduğuna göre alanı kaç
birimkaredir?
2) Tabanları 14 ve 34 olan bir ikizkenar yamuğun, çevresi ise 100 olduğuna göre alanı kaçtır?
3) Köşeleri (‒1,‒1), (5,3), (‒7,8) olan bir dik üçgenin çevrel çemberinin yarıçapı kaçtır?
4) ABC üçgenin m(A) = 500 , B köşesinin dış açısı 940. Buna göre C açısı kaç derecedir?
5) Bir dik üçgenin bir açısı 620 olduğuna göre dik üçgenin hipotenüsüne indirilen yüksekliği
ve açıortaya arasındaki açının derecesi bulunuz.
A) 44
B) 17
C) 6,5
D) 480
E) 576
9. Aşağıdaki ifadeleri çözünüz ve çıkan sonuçlarına göre küçükten büyüğe doğru sıralayınız:
1) log0,5 5 64
2) log81 log9 2 8
 
log
6
3) 9 3 3
4) log3 32  log2 25 log0, 2 3
5) log14 56  log14 686
10. Doğruları eğimlere göre (en büyükten başlayarak)sıralayınız:
1) 0,1x + 0,01у = 0,001
2) 0,16х + 0,25у = 36
3) 8х ‒ 5у = 40
4) 12х + 3у = 4
5) 25х ‒ 16у = ‒9
3.Bölüm. 8 puan değerinde sorular.
11.-12. uygun eşleştirme, 13.-14.sorularda uygun sıralama yapılacaktır. Cevap, her kare içine bir harf
veya rakam olarak yazılacaktır ( Örnek 11.-12.sorularda -1A2B3C4D5E, 13.-14.sorularda- 13425 ).
15.1–15.4 alt sorularda verilmiş seçeneklerden bir doğru vardır. Cevap numaraları cevaplar
tablosuna yazınız. Büyük harf ve kitap harfi (el yazısı değil ) kullanınız. Nokta, virgül ve diğer
işaretleri kullanmayınız.
11. Aşağıda verilen fonksiyonları grafikleriyle eşleştiriniz.
А)
1) y  3 x 1  1
1
2) y   
2
3) y  2
x 1
B)
C)
x
4) y  3 x  1
D)
12. Uygun eşleştirmeleri yapınız:
1)
1
1
log2
3
1024
А)
7
 5x  6
2x  3
2) ‒e
В) x 2  2 x  3
3) π
С) 3  2 x  11
4)  e 2 2
D) x 2  4 x   x 2  9  4 x  9
13. Aşağıdaki ifadeleri çözünüz. Sonuçları, her sayıya eşit olan sonucun harfı yazınız ve cevap tablosuna
Oluşmuş matematik terimi yazınız.
 16 
3
9
2
 320, 2
24
-M


21  2 25  2 84 - L
58 
7
3
-M

7 3
7 3
442  262
-İ
35
3
88  30 7  3 7 - E

11 6 0,5  3
12 3  2 2
2



 1,50

2
-Y


28  10 3 5  3 - U
2
-N
8

0 , 25 8
17
‒5
2,75
0,81
22
2,5
‒8
14. Aşağıda verilen şekilleri çizginin eğimlerinin artışına göre sıralayınız:
1)
3)
4)
7)
8)
2)
5)
6)
15. [‒5;5] aralığında y = f(x) ve y = g(x ) fonksiyonların grafikleri şekilde gösterilmiştir.
15.1. y = f(x) fonksiyonun değeri, y = g(x) fonksiyonun değerinden daha büyük olmaması için x kaç
olmalıdır?
1)  5;4  2;1
2)  3;2 1;5
3)  4;2 1;5
4)  4;3   3;2 1;5
15.2. f(x) ≤ g(x) eşitsizliğini sağlayan en küçük, negatif olmayan ve tamsayı değeri aşağıdakilerden
hangisidir?
1) 1
2) 0
3) 5
4) ‒1
15.3. g(x) > 0 eşitsizliğin kaç tane tamsayı çözümü vardır?
1) 0
2) 2
3) 3
4) 7
15.4. Verilen aralıkta g(x) fonksiyonun en büyük ve en küçük değerlerinin toplamı aşağıdakilerden
hangisidir?
1) 2
2) 1
3) ‒3
4) 0
4.Bölüm. 16.soru 20 puan değerindedir.
16.soruda 4 alt soru vardır ve her alt soru 5 puan değerindedir. Cevap her kare içine bir harf olarak
boşluk bırakmadan yazınız. Virgül ve diğer işaretleri kullanmayınız. Büyük harf ve kitap harfi (el
yazısı değil ) kullanınız.
2 x  3
 2 cos x denklemi çözünüz.
16. sin( x   )  cos
2
16.1. Denklemin en büyük negatif kökü х0 bulunuz. Cevap tablosuna,
х0

’ye eşit sayı ondalık kesir olarak
yazınız.
16.2. x0 ‒ bu denklemin en küçük pozitif kök olduğuna göre tgx0 değerini bulunuz.
16.3. [‒5,5π;‒3π] aralığında denklemin kaç kök olduğunu bulunuz.
16.4. [‒5,5π;‒3π] aralığında denklemin köklerinin toplamı bulunuz. Toplamı π ile bölünüz ve sonuç cevap
tablosuna yazınız.
Ural Federe Bölgesi Öğretmen Evi
IX. Bilim Temelleri Bilgi Yarışması
PREMİER LİG 2012-2013 öğretim yılı
Matematik
Maxim Kontsevich ‘e ithafen
Final
11.sınıf
Cevap anahtarları
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15.1
15.2
15.3
15.4
16.1
16.2
16.3
16.4
1
1
1
1
1
1
1
1
2
5
1
1
5
8
3
3
4
5
3
2
4
8
3
2
2
3
3
B
D
E
3
3
D
D
1
3
5
4
3
4
4
2
2
2
4
4
2
2
2
5
E
А
C
5
2
B
H
8
1
3
3
3
1
1
3
3
4
4
D
C
А
4
4
4
А
E
B
5
5
5
C
B
D
E
F
3
2
4
4
7
7
А
А
6
6
5
5
C
B
6
6
H
G
7
7
F
C
8
8
G
E
8
1.Bölüm. 3 puan değerinde sorular. 1.-5. sorularda beş seçenekten üç doğru cevabı seçiniz.
Cevaplar her rakam her kare içinde boşluk bırakmadan yazınız.
1. Doğru ifadeleri seçiniz:
1) iki yan yüzü tabana dik olan bir üçgen piramit vardır.
2) yan yüzleri tabana dik olan bir üçgen piramit vardır.
3) iki yan yüzü tabana dik olan bir dikdörtgen piramit vardır.
4) üç yan yüzü tabana dik olan bir dikdörtgen piramit vardır.
5) iki bitişik yüzü tabana dik olan bir dikdörtgen piramit vardır.
2. у=f(х) fonksiyonu ( – 5; 11) aralıkta bulunmaktadır. Bu fonksiyonun türevinin grafiği şekilde
gösterilmiştir.Buna göre aşağıdakilerden hangileri doğrudur:
1) ( – 4; – 1) aralığında fonksiyon azaladır.
2) fonksiyonun artış aralığın en büyük uzunluğu10’dur.
3) fonksiyonun iki maksimum noktası vardır.
4) fonksiyonun iki minimum noktası vardır.
5) fonksiyon grafiğin teğeti, у=2 doğrusuna paralel üç
noktasında olabilir.
3. Dikdörtgenler prizmasi ile ilgili doğru ifadeleri seçiniz:
1) kesit yamuk olabilir.
2) tüm tepe noktalarından eşit mesafede bulunan bir noktası vardır.
3) prizmanın simetri ekseni vardır.
4) diyagonal(cisim köşegeni) kesiti her zaman karedir.
5) diyagonal(cisim köşegeni) ,aynı zamanda da simetri doğrusudur.
4. Aşağıdaki ifadelerden doğru olarak tamamlayınız:
…………… , bu olayın olasılığı %50 den fazla olamaz.
1) Zar attığında çift sayı gelmesini,
2) 2 zar attığında toplam en fazla 7 gelmesini
3) sırayla iki sefer iki zar attığında 1 veya 6 hiç gelmemesini
4) sırayla üç sefer iki zar attığında en az bir seferinde puan sayısının toplamı 10 ve fazla gelmesini,
5) sırayla üç sefer iki zar attığında her seferinde farklı puan sayısının gelmesini
5. Belirli 20 sorunun sorulacağı bir sınavda bir öğrenci, 12 soru ezberledi,5 soruya hiç bakmadı, diğer
soruların ise bazılarını biliyor bazılarını bilmiyor. Sınavda 3 soru sorulacak. Buna göre doğru ifadeleri
seçiniz:
1) olabilecek tüm üçlü soru kombinasyonlar 1140’dır.
2) olabilecek tüm üçlü soru kombinasyon arasında öğrenci tüm soruları 180 kombinasyonda bilir.
3) olabilecek tüm üçlü soru kombinasyonlarından tüm çeşit sorular ( 1 soru ezberlenmiş, 1 soru hiç
bakmamış ve 1 soru biliyor bilmiyor) toplam 180 tane vardır.
4) üçlü soru kombinasyonlarından 748 tanesini öğrenci ezberlemiş.
5) olabilecek tüm üçlü soru kombinasyonlarından öğrenci 15 tane bilmiyor
2.Bölüm. 5 puan değerinde sorular. 6.-8. sorularda uygun eşleştirmeleri yapınız.
Cevap her kare içine bir harf olarak yazınız. Büyük harf ve kitap harfi (el yazısı değil ) kullanınız.
6. Aşağıda verilen fonksiyonları kök sayıları ile eşleyiniz.
f(x) fonksiyonu
1
1) f(x) =
х
2) f(x) = tgx
3) f(x) = 2 cos x
4) f(x) = 3  log1 x
2
denklemin kök sayısı
А) kök yoktur
B) bir
C) iki
D) üç
5) f(x) = 3 – х
E) sonsuz sayıda
7. Uygun eşleştirmeleri yapınız:
Türev grafikler
Fonksiyon grafikleri
А)
1)
2)
B)
3)
C)
4)
D)
5)
E)
8. Uygun eşleştirmeleri yapınız:
Problem şartları
1) Bir doğru üzerinde cisim hareket ettiğinde S mesafesi А) 36
S(t)= 7t – 4 formülüne göre değişiyor. Hareket başladıktan 3.
saniyedeki hızı kaçtır?
2) Bir doğru üzerinde cisim hareket ettiğinde S mesafesi B) 13
S(t)= 3t2 – 2t – 7. formülüne göre değişiyor. Hareket
başladıktan 2. saniyedeki hızı kaçtır?
3) Bir doğru üzerinde cisim hareket ettiğinde S mesafesi C) 10
S(t)= 2t3 – 3t2 + 1 formülüne göre değişiyor. Hareket
başladıktan 3.saniyedeki hızı kaçtır?
4) Bir doğru üzerinde
cisim hareket
ettiğinde S mesafesi D) 1 + 2е
Cevap
S(t)= t3 + 2lnt + 5 formülüne göre
başladıktan 2. saniyedeki hızı kaçtır?
değişiyor. Hareket
5) Bir doğru üzerinde cisim hareket ettiğinde S mesafesi S(t)= E) 7
t2
 2e t formülüne göre değişiyor. Hareket başladıktan 1
2
saniyedeki hızı kaçtır?
9.soruda uygun sıralamaları yapınız. Cevap her kare içinde bir rakam olarak boşluk bırakmadan
yazınız. Virgül ve diğer işaretleri kullanmayınız.
9. Bu bilgi yarışması; Fields ödülü alan rus kökenli fransız matematikçi Maxim Kontsevich’e ithaf
edilmiştir. Maxim Kontsevich ile ilgili verilen ifadelerin kronolojik sıralamasını yapınız:
1)Maxim Kontsevich Forbes derginin reytingine göre dünyaca en ünlü rus kökenli 10 bilimadam arasında
yer aldı.
2) M.Kontsevich Moskova Devlet Üniversitesi mekanik-matematik fakültesi bitirdi.
3) M.Kontsevich Bonn Üniversitesi'nde PhD derecesini aldı.
4) M.Kontsevich Poincare ödülü almıştır.
5) Witten'in hipotezsi kanıtığı için Fields ödülü aldı.
10. Aşağıda verilen fonksiyonların x= х0 noktasındaki teğetilerinin yaptıkları pozitif yöndeki açıları
büyükten küçüğe doğru sıralayınız:
1) f(x) = cos(x), х0=
2) f(x) =2∙ sin(

6
3

), х0=
2
3
3) f(x) = ln x – 1, (1, 0)
1
4) f(x)=х3+1, х0= 
2
5) f(x)= 2ex, x0 = ln2
3.Bölüm. 8 puan değerinde sorular.
11.-12.sorularda uygun eşleştirmeleri yapınız. Cevap her kare içinde bir harf olarak boşluk
bırakmadan yazınız. Büyük harf ve kitap harfi (el yazısı değil ) kullanınız.
11. f(x)= |x – 1|– 2 ise integralleri hesaplayıp uygun eşleştirmeleri yapınız:
İntegral
3
 f ( x )dx
İntegral değeri
А) – 3
1) 0
2
2)
 f ( x )dx
B) 1,5
3
C) – 2
4
3)

f ( x )dx
2
4
4)
 f ( x )dx
2
E) 0
3
5)

f ( x )dx
3
F) 0, 5
4
6)

f ( x)dx
3
1
7)

G) 2
f ( x )dx
2
H) – 1
1
8)
D) – 3,5

f ( x )dx
3
12. İkinci sınıf tren vagonunda 54 oturma yeri ( 9 kabin: 4 ön ( 2 alt/ 2 üst) ve 2 yan ( 1 alt / 1 üst) oturma
yeri ) vardır. Çift sayılı - üst, tek sayılı – alt oturma yerleridir. Bir yolcu tren bileti alırken oturma yeri
rastgele belirtilmiştir. Buna göre aşağıdaki eşleştirmeleri yapınız.
Olay (A)
Olasılık P(A)
1) alt yan oturma yerine bilet alma olayı
1
А)
4
2) üst yan oturma yerine bilet alma olayı
2
B)
3
3) alt oturma yerine bilet alma olayı
9
C)
17
4) 1.-35. oturma yerleri satıldığında, alt oturma yerine bilet alma olayı
1
D)
3
5) 3/1’i oturma yerleri satıldığında, alt oturma yerine bilet alma olayı
13
E)
22
6) 1.-32. oturma yerleri satıldığında, üst yan oturma yerine bilet alma
1
F)
olayı
2
7) 1.-20. oturma yerleri satıldığında, yan oturma yerine bilet alma
9
G)
olayı
22
8) 1.-20. alt oturma yerleri satıldığında, ön oturma yerine bilet alma
1
H)
olayı
6
13.-14.sorularda doğru sıralamaları yapınız.Cevap her kare içinde bir harf olarak boşluk bırakmadan
yazınız. Büyük harf ve kitap harfi (el yazısı değil ) kullanınız.
13. Sayıları küçükten büyüğe doğru sıralayınız:
5) cos (  )
5
1) sin( 
)

12
6) ctg( )
6
13
2) cos (
)

24
7) tg( )
4
5
3) sin(
)
8)
sin(0)
24
17
4) sin(
)
6
14. Metinde boş bırakılan yerleri uygun ünlü matemitikçilerin isimleri ile tamamlayınız. Cevaplar
tablosuna, metin içinde bunların sırayla gelen numaraları yazınız
XII. yüzyılda yaşamış Hint matematikçi _____________ (1114 – 1185) «Lilavati » eserinde
kombinasyon ve permütasyon ile ilgili problemlerin araştırmaları yapmış. Kombinatorik, genellikle
sonlu soyut nesneleri konu alan pür matematik dalı XVI.yüzyılında ortaya çıkmış. Zar ouynlarında farklı
seçenek olasılığı ile ilk araştırmaları italyan matematikçi __________________(1499-1557) başlamıştır.
Kombinatorik teoretik araştırmaları XVII yüzyılında fransız bilimadamları Blaise Pascal (1623-1662) ve
____________(1601-1665) yapmışlardır.Bundan miza problemi önemli bir rol oynamıştır. Bu
problemi
_____________________ çözmüştür. Bu problemin çözümü « matematiksel beklenti » kavramının
tanıtılmasına yol açmıştır. Daha sonraki kombinatorik gelişiminde, isviçre matematikçi
________________ 1654-1705), alman matematikçi _____________(1646-1716),
_________________(1707-1783) yer almışlardır. Ancak onların araştırmalar da farklı oyunlara( loto,
soliter oyunu, v.s.) bağlıydı.
Modern kombinatorik babası olarak, kombinatoryal olasılık analizi yapan, Macar matematikçi
____________ (1913-1996) kabul edilir.
1) Blaise Pascal
4) Jakob Bernoulli
7) Leonard Euler
2) Gottfried Leibniz
5) Pierre de Fermat
8) Bhaskara
3) Niccolo Tartaglia
6) Pal Erdos
15.1–15.4 alt sorularda verilmiş seçeneklerden bir doğru vardır. Cevap numarası cevaplar
tablosuna yazınız.
15. Problemleri çözünüz:
15.1 Ayşe bir piramide bakmış ve üç sayı toplamış.Buna göre bir piramidin tepe noktaların sayısı ,
kenar sayısı ve yüzey sayısı toplamı kaç olabilir?
1) 28
2) 29
3) 30
4) 31
5) 32
15.2 Aytaç atış etmeye öğreniyor. Bir ay önce ilk derste 100 atıştan 40 atış başarılıydı. Bugün 200
atıştan Aytaç’ın başarılı atış oranı % 80 artmıştır. Aytaç bugün kaç başarılı atış yapmış.
1) 120
2) 140
3) 144
4) 160
5) 240
15.3 Bir çiçekçinin 84 kırmızı, 24 beyaz ve 36 sarı gülü vardır. Tüm mevcut gülleri kullanarak aynı
buket kaç tane yapılabilir?
1) 4
2) 6
3) 8
4) 12
5) 18
15.4 Sayı bilmecesinde KAN – GAR = OO farklı harfler farklı sayıya, aynı harfler aynı sayıya eşittir.
KAN sayı en büyük olduğuna göre N sayı kaçtır?
1) 8
2) 7
3) 6
4) 5
5) 4
4.Bölüm. 16.soru 20 puan değerindedir.
16.soruda 4 alt soru vardır ve her alt soru 5 puan değerindedir. Cevap her kare içine bir harf
olarak boşluk bırakmadan yazınız. Virgül ve diğer işaretleri kullanmayınız. Büyük harf ve kitap
harfi (el yazısı değil ) kullanınız. Ondalık kesir virgül ile yazınız.
16. Problemleri çözünüz:
16.1 13  13  x  x denkleminin çözüm kümesini bulunuz.
67
67
67
67
 20052005
 20052007
 20052004
16.2 20052006
ifadesinin sonucu kaçtır?
12345
12345
12345
12345
16.3 Her gün aynı saatte Ahmet amca arabayla işe gidiyor. Ahmet amcanın ortalama hızı 40 km/s. saat
08:03’te, ortalama hızı 60 km/s. iken saat 07:57de iş yerine varıyor. Saat tam 08.00’te iş yerine
varabilmesi için Ahmet amcanın ortalama hızı kaç olmalıdır?
16.4 Köyde 250 hobbit yaşar. Her hobbitin ayrı bir evi vardır. Akşam hobbitler bir birine ziyaret ederler.
Bir akşamda her hobbit, evde bulunabilecek herkese ziyaret eder ve kendisi de bu akşam evde
bulunmaz. En az kaç akşam geçtikten sonra herhangi iki hobbitten biri diğerine ziyaret edebilecektir?
Ural Federe Bölgesi Öğretmen Evi
XI. Uluslararası Bilim Temelleri Bilgi Yarışması
2014-2015 eğitim-öğretim yılı
Final Premier lig
Matematik 11.sınıf
Cevap anahtarları
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
1
2
3
4
5
6
7
8
1
1
1
1
1
1
1
1
3
2
3
2
2
D
C
C
5
4
4
3
5
2
2
2
A
E
A
3
3
3
B
A
B
4
4
4
C
B
D
5
5
5
E
D
E
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
9
10
11
12
13
14
15.1
15.2
15.3
15.4
16.1
16.2
16.3
16.4
5
1
1
1
1
4
4
0
9
9
5
2
4
4
D
C
3
3
3
2
2
2
2
2
1
3
C
D
4
1
2
5
3
3
B
B
4
4
A
A
2
9
0
0
0
0
1.Bölüm. Her soru 3 puan değerindedir. 1.-5. soruların altı seçenekten üç doğru cevabı vardır.
Doğru yanıtların numaralarını cevaplar tablosuna yazınız.
1. [2; 4] aralığına ait değerler aşağıdakilerden hangileridir?
1) log3 54 – log3 2
3) ( 2 5 )2 : 10
2) ( 5  2 )2  4 5
5) ( 14  10 )  14  10 )
6)( 48∙sin386°):sin26°
4) (19∙cos45°):sin45°
2. ax = b denklemin var olma şartları aşağıdakilerden hangileridir?
1) a > 0
4) b > 0
2) a ≠ 1
5) b ≠ 0
3) a=0
6) b ≠ 1
3. Okula yazı tahtası, masa, bilgisayar ve yazıcı satın alınmıştır. Bilgisayar, yazıcının ve masanın
toplamından daha pahalı, yazıcı ise masa ve tahtanın toplamından daha pahalı olduğu bilinmektedir.
Buna göre aşağıdakilerden hangileri doğrudur?
1) bilgisayar tahtadan daha pahalıdır
2) masa tahtadan daha pahalıdır
3) bilgisayar satın alınan eşyalardan en pahalısı
4) bilgisayar ve yazıcı toplamında iki masa ve tahta toplamından daha pahalıdır
5) tahta yazıcıdan pahalıdır
6) yazıcı masadan ucuzdur
4. Aşağıdakilerden hangileri fraktaldır?
1) Serpinskiy halısı
4) Newton havuzları
2) Koch eğrisi
5) Mandelbrot kümesi
3) Menger süngeri
6) Julia kümesi
5. Düzlemsel şekillerin döndürülmesi ile oluşan geometrik cisimler aşağıdakilerden hangileridir?
1)
2)
3)
4)
5)
6)
2.Bölüm. 6.-10.sorular. Her soru 5 puan değerindedir.
6. - 8.sorularda uygun eşleştirmeleri yapınız. Eşleştirdiğiniz rakam ve harfi cevaplar tablosuna
örnekteki gibi yazınız. ÖRNEK:
1 A 2 C 3 B 4 D 5 E
6. 1 cm x 1 cm karelerden oluşan kareli defterde, çizilen şekillerin alanlarını bularak uygun eşleştirmeleri
yapınız.
1)
2)
3)
4)
5)
A) 9 cm2
B)16 cm2
C)28 cm2
D)12cm2
E)20 cm2
7. Problemleri , doğru cevaplarıyla eşleştiriniz.
Soru
1) Bir mağaza, sivrisinek ilacının şişesini 120 rubleden alıp %35 kârla satmaktadır. Bu
mağazadan 900 rubleye en fazla kaç şişe alınabilir?
2) Bir şehrin nüfusu 200 000 kişi. Nüfusun %10’u çocuk ve ergendir. Yetişkinlerin
%50’si ise çalışmamaktadır (emekliler, öğrenciler).Buna göre şehirde çalışan yetişkin
sayısı kaçtır?
3) %15’i tuz olan 6 litrelik bir tuz-su karışımına, 4 litre su eklenirse, karışımın tuz oranı
kaç olur?
4) Bir okuldan mezun olan 8 kişi diğer şehirlerde eğitimlerine devam edecekler. Bu
kişiler, toplam mezun olanların sayısının %5’i olduğuna göre okuldan kaç kişi mezun
olmuştur?
5) Bir dolmuşta bir yolculuk ücreti 2 liradır. Yolculuk ücretinde %30 artış olduktan sonra
160 lira ile en fazla kaç yolculuk yapılabilir?
8. Eşitsizlikleri çözümleri ile eşleştiriniz:
Eşitsizlik
1) (x – 1)·(x – 2) ≤ 0
2) (x – 1):(x – 2) ≤ 0
3) 1:((x – 1)·(x – 2)) < 0
4) –(x – 1):(x – 2) < 0
5) –(x – 1)·(x – 2) ≤ 0
Cevap
A) 9
B) 160
C) 5
D) 61
E) 90.000
Cevap
А) 1 ≤ x < 2
B) 1 < x < 2
C) 1 ≤ x ≤ 2
D) x < 1, x > 2
E) x ≤ 1, x ≥ 2
9.-10.sorularda uygun sıralamaları yapınız. Yaptığınız sıralamayı cevaplar tablosuna örnekteki gibi
yazınız. ÖRNEK:
1
3 5 2 4
9. İfadelerin değerleri bularak büyükten küçüğe doğru sıralayınız:
1) sin30°∙(sin12°∙cos 18° + cos12°∙sin18°)
4) 1 – (cos45°∙cos15° – sin15°∙sin45°)2
2) sin10°∙sin 50°∙sin 70°
5) (sin75°∙cos15° – sin15°∙cos75°)2 + 0,5
3) cos15°∙cos45° – cos45°∙cos75°
10. Denklemlerin köklerini bularak küçükten büyüğe doğru sıralayınız:
1) log2(4 − x) = 8
3) log3(x + 2) = 2
4) (x + 7)3 = 216
2) 32  4 х  4
5) 2 х  31  9
3.Bölüm. 11.-15.sorular. Her soru 8 puan değerindedir.
11. - 12.sorularda uygun eşleştirmeleri yapınız. Eşleştirdiğiniz rakam ve harfi cevaplar tablosuna
örnekteki gibi yazınız. ÖRNEK:
1 A 2 C 3 D 4 B
11. Aşağıdaki eşitsizliklerin çözüm kümelerini, sayı doğrusundaki görüntüleri ile eşleştiriniz.
Eşitsizlik
Çözüm kümesi
х
1) 0,5 ≤ 2
А)
2) 2х ≥ 2
В)
3) 2х ≤ 2
С)
4) 0,5х ≥ 2
D)
12. Grafikte, bir otomobilin motor gücünün(tork) bağıntısı gösterilmiştir. Apsis ekseninde dakikada devir
sayısı gösterilmiştir. Ordinat ekseninde ise tork (N∙m) olarak gösterilmiştir. Grafiği kullanarak motorun
devir sayısı aralığını, bu aralıktaki motorun tork bağıntısının özelliği ile eşleştiriniz.
İşlem durum özellikleri
1) tork değişmemiş
2) tork düşmüş
3) torkun maksimum artışı yapmış
4) tork 60 N∙m geçmemiş
Devir aralıkları
А) 0 – 1 500 d/dak.
В) 1 500 – 2 000 d/dak.
С) 2 500 – 4 000 d/dak.
D) 4 000 – 6 000 d/dak.
13. - 14.sorularda uygun sıralamaları yapınız. Yaptığınız sıralamayı cevaplar tablosuna örnekteki
gibi yazınız. ÖRNEK:
1
3 4 2
13. Soruların cevaplarını bularak değerleri küçükten büyüğe doğru sıralayınız:
1) Ali, demir parayı yazı çıkana kadar atmaktadır. Tam 4 kez atma olasılığı nedir?
2) 0-999 aralığından rastgele alınan bir sayının 449'dan büyük olma olasılığı nedir?
3) Bir parti ihraç malında 1050 parça ürün bulunmaktadır. Bunlardan 630 tanesi A tipidir; diğerleri ise B
tipidir. Rastgele alınan parçanın B tipi parça olma olasılığı nedir?
4) 75 paraşütten 6'sı arızalıdır. Rastgele alınan paraşütün arızalı olmama olasılığı nedir?
14. Denklemleri verilen doğruların eğimlerini büyükten küçüğe doğru sıralayınız:
1) 0,2x + 0,02у = 0,002
2) 0,17х + 0,26у = 42
3) 9х – 6у = 20
4) 13х – 2у = 6
15.soruda 4 alt soru vardır. Cevabı, her kare içine bir rakam gelecek şekilde boşluk bırakmadan
cevaplar tablosuna yazınız. Cevabı rakamla yazınız.
15. Resimde y = f (x) fonksiyonun grafiği gösterilmiştir. Grafiği kullanarak, soruları çözünüz.
15.1. f (x) en büyük değerini bulunuz.
15.2. f (x) en küçük değerini bulunuz.
15.3. f(2) bulunuz.
15.4. f (x) = 0 denkleminin en küçük kökünü bulunuz.
4.Bölüm. 16.soru 20 puan değerindedir.
16.soruda 4 alt soru vardır ve her alt soru 5 puan değerindedir. Cevabı, her kare içine bir rakam
veya harf gelecek şekilde boşluk bırakmadan yazınız. Ondalık kesri yazabilmek için virgül işareti
kullanınız.
16. Veli, Paşa ve Mikail aynı anda 1 km lik koşu yarışına başlar. Veli yarışı bitirdiğinde Paşa 100 m
arkasındaydı, Mikail ise Paşa'nın 90 m arkasındaydı. Paşa, Veli'ye göre 18 saniye daha geç koşuyu
bitirmiştir. Her birinin hızı tüm mesafe boyunca sabit olduğu bilinmektedir.
16.1. Paşa koşuyu bitirdiğinde Mikail kaç metre koşmuş olur?
16.2. Mikail 18 saniyede kaç metre koşar?
16.3. Mikail'in hızı kaç (m/s olarak)?
16.4. Mikail, Paşa'ya göre kaç saniye geç gelir?