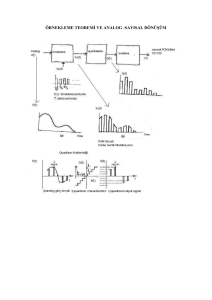
LOGARİTMA
ÜSTEL FONKSİYON
f:R " R +, f(x) = a x (a ! 1, a ! R)
bire - bir (1 - 1) v e örten fonksiyonuna
ÖRNEK:
x
f: R " R, f(x) = c1 m ,
3
fonksiyonunun değişimini inceleyelim.
üstel fonksiyon denir.
Örneğin; f:R " R+, f(x) = 2 x,
x
+
f:R " R , f(x) = c 1 m
3
fonksiyonları üstel fonksiyonlardır.
ÖRNEK:
f:R " R+, f(x) = 2 x,
fonksiyonunun değişimini inceleyelim.
Örneklerde gördüğümüz durumları
şu şekilde genelleyebiliriz.
a21
olmak üzere,
f (x) = ax fonksiyonunun
grafiği aşağıdaki gibidir.
1/a
1
a
-1
1
0 1 a 1 1 olmak üzere,
f (x) = ax fonksiyonunun
grafiği aşağıdaki gibidir.
a
-1
1/a
1
1
ÖRNEK:
ÖRNEK:
x
f: R " R + , f (x) = 3 - 2
+
f: R " R , f (x) = 4
x +2
fonksiyonunun grafiğini çiziniz.
fonksiyonunun grafiğini çiziniz.
ÖRNEK:
NOTLAR:
f: R " R +, f (x) = a 1 k + 2
2
x
fonksiyonunun grafiğini çiziniz.
LOGARİTMA
f(x) = a x fonksiyonunun ters fonksiyonuna
logaritma fonksiyonu denir ve f - 1 (x) = log a x
şeklinde gösterilir.
a ! R + - " 1 , olmak üzere,
f:R " R +, f(x) = a x , f - 1:R + " R, f - 1 (x) = log a x dir.
Tanıma göre,
y = a x , x = log a y
ÖRNEK:
Aşağıdaki soruları cev aplayınız.
a) log a 16 = 2 & a = ?
b) log n 125 = 3 & n = ?
olur.
ÖRNEK:
Aşağıdaki soruları cev aplayınız.
a) 5 x = 4 & x = ?
c) log 3 27 + 2 = x & x = ?
d) log 2 27 & x = ?
3 8
b) 3 - x = 7 & x = ?
ÖRNEK:
c) 2 x + 2 = 5 & x = ?
d) 6 - x - 1 = 3 & x = ?
ÖRNEK:
Aşağıdaki fonksiyonların tersini bulunuz.
a) f(x) = 5 x
b) f(x) = 3
c) f(x) = a 2 k
3
Aşağıdaki soruları cev aplayınız.
a) log 3 x = 2 & x = ?
ÖRNEK:
b) log 2 (x + 1) = 3 & x = ?
c) log 2 x + 1 = 3 & x = ?
d) log 1 ^ 2x - 1h = 2 & x = ?
3
x -2
x+1
ÖRNEK:
Aşağıdaki fonksiyonların terslerini bulunuz.
x
a) f(x) = 3 + 5
LOGARİTMA FONKSİYONUNUN
TANIM ARALIĞI
f(x) = log h (x) (g(x)) fonksiyonunun
b) f(x) = 7
x -3
tanımlı olması için ;
h(x) 2 0, h(x) ! 1 ve g(x) 2 0
-4
olmalıdır.
1 -x
c) f(x) = a 2 k
-3
5
ÖRNEK:
f(x) = log 3 (x + 3)
fonksiyonunun
en geniş tanım aralığını bulunuz.
ÖRNEK:
Aşağıdaki fonksiyonların terslerini bulunuz.
a) f(x) = 1 + log 3 ^ x + 1 h
b) f(x) = 2 - log 4 ^ x - 1h
ÖRNEK:
f(x) = log 3 (3x - 4)
c) f(x) = 3 + log 3 ^ 2x - 1 h
fonksiyonunun
en geniş tanım aralığını bulunuz.
5
ÖRNEK:
log 3 ^ log 2 x + 1 h = 2 & x = ?
ÖRNEK:
f(x) = log x (x + 2)
fonksiyonunun
en geniş tanım aralığını bulunuz.
DOĞAL LOGARİTMA FONKSİYONU
ÖRNEK:
2
f(x) = log^ 2 -xh (x - x - 20)
fonksiyonunun
en geniş tanım aralığını bulunuz.
f (x) = lo g a x fonksiyonunda a = e alınırsa
f (x) fonksiyonuna doğal logaritma fonksiyonu
denir ve log e x = lnx şeklinde gösterilir.
ÖRNEK:
lnx = 3
olduğuna göre x kaçtır?
ÖRNEK:
ln6log^ lnx h @ = 0
olduğuna göre x kaçtır?
ONLUK LOGARİTMA FONKSİYONU
f (x) = lo g a x fonksiyonunda a = 10 alınırsa
f (x) e onluk logaritma fonksiyonu denir
ve logx şeklinde gösterilir.
ÖRNEK:
ÖRNEK:
logx = 3 olduğuna göre x kaçtır?
f(x) = 2 + ln^ 3x - 1 h olduğuna göre
f -1 ^ x h
fonksiyonunu bulunuz.
ÖRNEK:
f(x) = 4 + log^ 2x - 2 h
f -1 ^ x h
olduğuna göre,
fonksiyonunu bulunuz.
LOGARİTMA FONKSİYONUNUN
ÖZELLİKLERİ
ÖZELLİK 1:
1 den farklı her pozitif reel sayının
aynı tabandaki logaritması 1 dir.
6 a ! R + - " 1 , olmak üzere,
log a a = 1
ÖRNEK:
x = log 3 3 + lne - log10
olduğuna göre x kaçtır?
ÖZELLİK 2:
1 in herhangi bir tabandaki
logaritması 0 dır.
6 a ! R + - " 1 , olmak üzere,
log a 1 = 0
ÖRNEK:
x = log 3 1 + (ln1). (log10)
olduğuna göre x kaçtır?
ÖZELLİK 4:
6 a ! R + - " 1 ,, x ! R + ve n ! 0
olmak üzere,
log an x = 1 .log a x
n
ÖRNEK:
log 0, 04 5 + log 27 3 + log
7
7 =?
ÖZELLİK 5:
ÖRNEK:
x24
olmak üzere,
log^ x -3h ^ x - 3 h + (lne). (log^ x -2h 1)
ifadesinin değeri kaçtır?
6 a ! R + - " 1 ,, x ! R + v e n ! 0
olmak üzere,
log an x m = m .log a x
n
ÖRNEK:
log 0, 09 81 + log 4 32 + log
5
25 = ?
ÖZELLİK 3:
6 a ! R + - "1 , v e x ! R +
olmak üzere,
n
log a x = n.log a x
ÖRNEK:
ÖZELLİK 6:
İki pozitif sayının çarpımınıın logaritması,
bu iki sayının logaritmalarının toplamına
eşittir.
a) log 3 8 = 3.t & t = ?
6 a ! R + - " 1 ,, x ! R +
olmak üzere,
log a ^ x.yh = log a x + log a y
b) log 5 125 = ?
ÖRNEK:
c) log100 - lne 3 = ?
log7 = a
olmak üzere, log70 ifadesinin a
türünden değeri kaçtır?
ÖRNEK:
ÖRNEK:
log8 = x
log 6 4 + log 6 9 = ?
olduğuna göre, log125 in x türünden
ifadesini bulunuz.
ÖRNEK:
log2 = a
olmak üzere, log5 ifadesinin
a türünden değeri kaçtır?
ÖZELLİK 8:
TABAN DEĞİŞTİRME
6 a, c ! R + - " 1 ,, b ! R +
olmak üzere,
b
log a b = log c
log c a
ÖRNEK:
log 2 ^ cot 1 c h + log 2 ^ cot 5 c h + log 2 ^ cot 9 c h + ...log 2 ^ cot 8 9 c h = ?
ÖRNEK:
log7 = a
4 olduğuna göre,
log5 = b
log 5 7 nin, a ve b türünden
değerini bulunuz.
ÖZELLİK 7:
İki pozitif sayının bölümünün logaritması,
bu iki sayının logaritmalarının farkına eşittir.
6 a ! R - " 1 ,, x, y ! R
olmak üzere,
x
log a a k = log a x - log a y
y
+
+
ÖRNEK:
x.y
k =?
z
a)
loga
b)
log 2 a 5 k = ?
16
SONUÇ 1:
6 a, b ! R + - " 1 ,, a, b ! R +
olmak üzere,
log a b = 1
log b a
SONUÇ 2:
6 a, b, c ! R + - " 1 ,, a, b, c, d ! R +
olmak üzere,
log a b.log b c.log c d = log a d
ÖRNEK:
ÖRNEK:
log 2 3.log 3 5.log 5 64 = ?
x log3 5 .5 log3 x = 25
olduğuna göre x kaçtır?
ÖRNEK:
ÖRNEK:
1
1
1
1
+
+
+
=?
log 2 120 log 3 120 log 4 120 log 5 120
ÖRNEK:
3
2
+
=?
log 2 72 log 3 120
ÖZELLİK 9:
a ! R+ - "1 ,, b ! R+
a loga b b
=
SONUÇ:
a logb c
= c logb a
olmak üzere,
dir.
3 k log3 4 .5 2k log5 8 = 32
olduğuna göre k kaçtır?