LYS – 1 / GEOMETRİ DENEME ÇÖZÜMLERİ
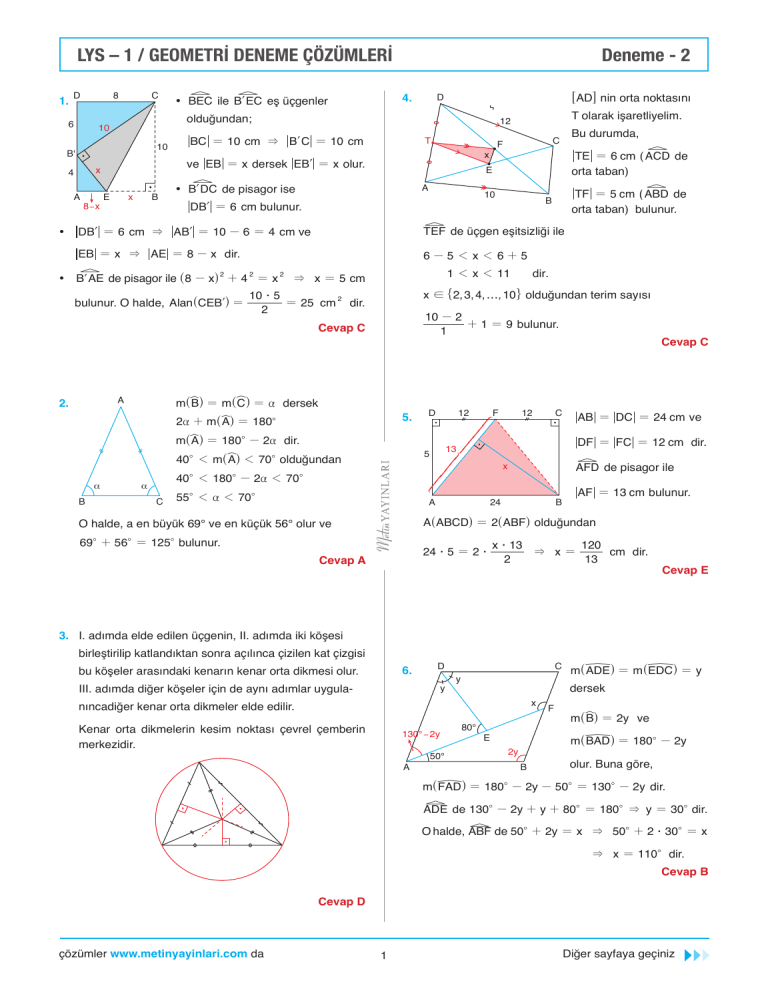
1.
D
8
6
C
10
B'
8−x
E
x
B
BC = 10 cm & BlC = 10 cm
T
6-5 1 x 1 6+5
1 1 x 1 11
10 - 2
+ 1 = 9 bulunur.
1
12
C
3
A
AB = DC = 24 cm ve
&
AFD de pisagor ile
x
44
55c 1 a 1 70c
Cevap C
DF = FC = 12 cm dir.
44
4
C
13
5
40c 1 180c - 2a 1 70c
F
42
40c 1 m ^W
Ah 1 70c olduğundan
12
D
14
5.
44
4
2a + m ^W
Ah = 180c
m ^W
Ah = 180c - 2a dir.
B
dir.
x ! "2, 3, 4, f, 10, olduğundan terim sayısı
10 $ 5
= 25 cm 2 dir.
2
m ^W
Bh = m ^X
Ch = a dersek
α
B
&
TEF de üçgen eşitsizliği ile
Cevap C
α
10
DBl = 6 cm bulunur.
&
∑ BlAE de pisagor ile ^8 - xh 2 + 4 2 = x 2 & x = 5 cm
A
&
TE = 6 cm ( ACD de
orta taban)
&
TF = 5 cm ( ABD de
orta taban) bulunur.
E
A
EB = x & AE = 8 - x dir.
2.
Bu durumda,
C
F
x
&
∑ BlDC de pisagor ise
bulunur. O halde, Alan ^CEBlh =
T olarak işaretliyelim.
12
∑ DBl = 6 cm & ABl = 10 - 6 = 4 cm ve
6AD@ nin orta noktasını
D
ve EB = x dersek EBl = x olur.
x
A
4.
olduğundan;
10
4
&
&
∑ BEC ile BlEC eş üçgenler
Deneme - 2
24
B
AF = 13 cm bulunur.
A ^ABCDh = 2 ^ABFh olduğundan
O halde, a en büyük 69° ve en küçük 56° olur ve
69c + 56c = 125c bulunur.
24 $ 5 = 2 $
Cevap A
3. I. adımda elde edilen üçgenin, II. adımda iki köşesi
120
x $ 13
cm dir.
& x=
2
13
birleştirilip katlandıktan sonra açılınca çizilen kat çizgisi
6.
bu köşeler arasındaki kenarın kenar orta dikmesi olur.
D
III. adımda diğer köşeler için de aynı adımlar uygula-
y
C
y
nıncadiğer kenar orta dikmeler elde edilir.
130° − 2y
A
m ^\
ADEh = m ^\
EDCh = y
dersek
x
Kenar orta dikmelerin kesim noktası çevrel çemberin
merkezidir.
Cevap E
80°
m ^W
Bh = 2y ve
m ^\
BADh = 180c - 2y
E
50°
F
2y
B
olur. Buna göre,
m ^\
FADh = 180c - 2y - 50c = 130c - 2y dir.
&
ADE
de 130c - 2y + y + 80c = 180c & y = 30c dir.
&
O halde, ABF de 50c + 2y = x & 50c + 2 $ 30c = x
& x = 110c dir.
Cevap B
Cevap D
çözümler www.metinyayinlari.com da
1
Diğer sayfaya geçiniz
LYS – 1 / GEOMETRİ DENEME ÇÖZÜMLERİ
y
3
44
2
4
44
44
4
1
3
7
2
15
B
24
açısı 110°, 120°, 130° ise bu köşelerdeki dış açılar
sırası ile 180° – 110° = 70°, 180° – 120° = 60° ve
180° – 130° = 50° dir.
pisagor ile OD = 24 cm
44
O
25
14
20
10.Konveks çokgen n kenarlı olsun. Bu çokgenin üç iç
&
AOB de pisagor ile
&
AO = 20 cm ve COD de
25
44
144424443
A
13
C
44
4
7.
Diğer n – 3 köşedeki iç açılar 160 ar derece olduğu için
dış açılar 20 şer derecedir. (180° – 160° = 20°)
bulunur. Bu durumda
D x
144424443
y
x
+
= 1 dir.
15
20
y
x
CD nin denklemi :
+ = 1 dir.
24
7
_
y
x
+
= 1b denklemleri birlikte çözüldüğünde
b
15
20
`
312
y
x
K noktasının apsisi x =
bulunur.
+
= 1bb
25
24
7
a
Bir çokgenin dış açıları toplamı 360° olduğu için
AB nin denklemi :
70° + 60° + 50° + (n – 3) $ 20° = 360° & n = 12 bulunur.
Cevap B
CEVAP C
11.
&
ABC de pisagor ile
8. y
B
=
a+b
b
a
a
5
b
A
b−a
C
a
O
^b - ah 2 + b 2 = ^a 5 h 2
C
B merkezli çeyrek
çemberin yarıçap
uzunluğuna r dersek,
r
A 1 E
& 2a 2 + ab - b 2 = 0
b
r−2
F
4
2
& 4a + 2ab - 2b = 0
x
3
4
& a 2 + b 2 - 2ab + b 2 = 5a 2
2
r+1
D
14444444244444443
Deneme - 2
r
14444444244444443
B
AB = DC = r + 1
FC = r - 2 olur.
r+1
& ^2a - bh $ ^a + bh = 0
EB = FB = r
&
FCB de pisagor uygularsak
& 2a - b = 0 0 a + b = 0
a
1
=
O halde, 2a - b = 0 & 2a - b = 0 &
dir.
b
2
^r - 2h 2 + 4 2 = r 2 & r = 5 bulunur.
Cevap E
Cevap A
E
9.
a
L
D
S3
K
B
dilimleri benzer olduğundan
&
&
10
OD
DC
DC
= % &
=
16
8
OA
AB
&
& DC = 5 cm
10
42
R
16
44
4
A
S1
S3
Aynı (O) merkezli daire
O
44
2a
S2
12.
44
P
C
144
S4 a
S4
RB ' CF ve
BK = CK olduğundan
&
&
KRB , KFC dir.
F
PD ' EC ve
CL = DL olduğundan
&
&
LPD , LEC dir.
A1
C
44
D
&
&
LPD , LEC olduğundan EL = LP = a diyelim.
LD
LP
&
&
=
& AP = 2a .
Buna göre LPD + APB &
AB
AP
&
&
A `APRj = S 1 , A ^PRKCLh = S 2 , A `KRBj = S 3 ve
44
6
3
A
5
A2
8
&
A `LPDj = S 4 dersek;
&
&
&
A `KCFj = S 3 `KRB + KFCj
&
&
&
A `LECj = S 4 `LPD + LECj
&
3S 1 = S 2 + S 3 + S 4 ( AFE de 6PR@ orta taban) olur.
3s1
O halde,
644474448
S + S2 + S3 + S4
4S 1
A ^AFEh
2
=
=
= 1
6S 1
3
2 `S 2 + S 3 + S 4 j
A ^ABCDh
144424443
Cevap B
3s
A1 + A2 =
ve A 1 =
B
Daire diliminin alanı gördüğü
yayın uzunluğu ile yarıçap
uzunluğunun çarpımının yarısı ile de bulunabilir. O halde,
16 $ 8
= 64 cm 2
2
10 $ 5
= 25 cm 2 dir.
2
2
Buna göre A 2 = 64 - 25 = 39 cm bulunur.
Cevap C
1
çözümler www.metinyayinlari.com da
2
Diğer sayfaya geçiniz
LYS – 1 / GEOMETRİ DENEME ÇÖZÜMLERİ
r
8−
B
15
15
O
T
−r
15 − r
C
1444444442444444443
F
%
m ^\
ABCh = 10c & m ^ADh = 20c
17
olduğundan
m ^\
BACh = 90c dir.
ADOE karesinin
kenar uzunluklarına
r dersek;
AD = r & BD = 8 - r & BT = 8 - r
& m ^\
DFAh = 10c dir.
%
m ^\
ACBh = 20c & m ^AEh = 40c
& TC = 15 - r & EC = 15 - r olur.
BC = 17 cm olduğundan
8 - r + 15 - r = 17 & r = 3 cm bulunur.
&
ADO da pisagor ile; AO = 3 2 cm bulunur.
&
ABC nin dik köşesine (A noktasına) çember üzerindeki
en yakın nokta P dersek;
& m ^\
EFAh = 20c dir
O halde,
8−r
r
4
10°
Pr
14
C
17 2 = 8 2 + 15 2
4
20°
r
E
42
D
D
r
44
4
E
20°
8
3
20°
A
44
10°
40°
r
44
44
3
B
16.
44
4
A
14
4
44
2
13.
Deneme - 2
m ^\
DFEh = a = 20c + 10c = 30c bulunur.
Cevap B
AP = AO - OP = ^3 2 - 3h cm bulunur.
Cevap A
17. A
P noktasından kuvvet ile
α
2α
P
2
PT
2
= PA $ PB
PT
2
= 2$8
S2
4
PT = 4 cm bulunur.
A
α
6
B
B
x+8
O
h1
h1
A
h
AO = x + 8 ve
OE = x + 2 olur.
x+2
A
A1
d1
OB = x dersek
E
d2
B
B1
x
B
8
C
C
C
C1
h2
h2
8
bulunur.
Cevap C
h + 2h1 + 2h2
h + h1 + h2 = 8
&
h 1 + h 2 = 8 - h dir.
A ^ABCh =
6$h
= 3h olduğuna göre
2
3 6 $ h + 2h + 2h
8–h
^
h
G
1
2
A `A 1 B 1 C 1 j =
= 3 8h + 2 ^h 1 + h 2hB
2
= 3 ^h + 16 - 2hh = 48 - 3h olur.
&
AEB de öklit uygulanırsa
^x + 2h 2 = x $ ^x + 8h & x = 1 cm bulunur.
O halde,
O halde,
küçük çemberin çapı = 2x + 8 = 2 $ 1 + 8 = 10 cm ise
10
= 5 cm bulunur.
yarıçap =
2
Cevap C
çözümler www.metinyayinlari.com da
3
S 1 - S 2 = ^14 - 4rh cm 2
18.
6
E
7
Cevap E
15.
4
ve BC = 4 + 3 = 7 cm dir.
Kırmızı taralı bölgenin alanına A dersek
4$7
2
S1 + A =
= 14 cm
2
90c
S2 + A =
$ r $ 4 2 = 4r cm 2
360c
TA
2
1
dir.
= =
4
2
TB
D
D
14444444244444443
&
&
Açı açı benzerliği ile TPA + BPT olacağından
&
A
S1
m ^\
TBAh = a dersek
%
m ^TAh = 2a ve m ^\
ATPh = a olur.
TA
PA
=
TB
PT
AB = BE = 4 cm (yarıçap)
144444244443
T
144424443
14.
A ^ABCh + A `A 1 B 1 C 1j = 3h + 48 - 3h = 48 cm 2
bulunur.
Cevap A
3
Diğer sayfaya geçiniz
Deneme - 2
19.
O1
2 r
1
R−2
Üst tabanın, alt tabanın ve
2
A
sırası ile r1, r2 ve R diyelim.
R
2
2
2
∑ rr 1 = 20r & r 1 = 20 cm
B
&
olduğuna göre, O 1 OA da
x
pisagor ile
r2
x
22.
kürenin yarı çap uzunluklarına
R
O
R−x
O2
LYS – 1 / GEOMETRİ DENEME ÇÖZÜMLERİ
^R - 2h 2 + r 21 = R 2 & R = 6 cm bulunur.
Şekilde üstten görünümü verilen bir küpün bir yüzeyinden 4 tane simetri düzlemi geçer.
∑ rr 22 = 32r & r 22 = 32 olduğuna göre,
Buna göre,
&
OO 2 B de pisagor ile;
∑ Üst ve alt yüzeylerden 4 tane
^R - xh 2 + r 22 = R 2 & ^6 - xh 2 + 32 = 6 2
∑ Sağ ve sol yüzeylerden 3 tane (1 tanesi üst ve alt
& x = 4 cm bulunur.
yüzeylerden sayıldığı için)
Cevap B
∑ Ön ve arka yüzeylerden 2 tane (1 tanesi alt ve üst, 1
tanesi ön ve arka yüzeylerden sayıldığı için)
20.
E
B
4
4
Toplam, 4 + 3 + 2 = 9 simetri düzlemi vardır.
Prizmanın üst tabanındaki EAB
4 3
Cevap E
ikizkenar üçgeninde
A
30° – 120° – 30° üçgeni ile
5
3
K
4
u - 2v
Yan yüzler tabana dik olduğu
için ABCD dikdörtgendir.
D
4
3
şekildeki u - 2 v vektörü elde edilir.
24. BA = ^- 1 - 3, 1 - 0, - 1 - 2h = ^- 4, 1, - 3h
olduğundan u = BA + v
O halde, prizmanın hacmine V dersek
4
ekleme yöntemi ile toplarsak
Cevap B
20 3 = 4 3 $ AD & AD = 5 br bulunur.
&
AKD de pisagor ile AK = 3 br bulunur.
V = e6 $
u ile - 2 v vektörlerini uç uca
- 2v
u
A ^ABCDh = 20 3 br 2 olduğuna göre,
2
u - 2 v = u + ^- 2 u h olduğundan
23.
AB = 4 3 br bulunur.
C
= ^- 4, 1, - 3h + ^3, 2, - 4h
o $ 3 = 72 3 br 3 dür
= ^- 1, 3, - 7h bulunur.
14243
taban alanı yükseklik
Cevap D
Verilen şartlara uygun 6AB@
y
25.
A
şekilde çizilmiştir.
3
21.
R
11
43
44
17
42
14
4
6
11
11
11
6
6
6
8
8
15
15
1444442444443
y
O
25 cm
x
AK = 3 br, KB = 2 br ve
K noktasının koordinatları
(x, y) olsun.
K(x, y)
y
2
P
B
x
x 2 + AR
2
= 3 2 & AR =
9 - x 2 dir.
&
&
ARK + KPB olduğundan
Verilen ifadeye uygun şekil yukarıdaki gibidir. Verilen
uzunlukları şekildeki dikdörtgenler ve dik üçgen üzerinde kullanırsak suyun yüksekliği en az 25 cm bulunur.
9 - x2
3
=
& 4x 2 + 9y 2 = 36 dır.
y
2
2
2
O halde K(x, y) noktaları 4x + 9y = 36 denklemli
elipstir.
Cevap A
Cevap D
çözümler www.metinyayinlari.com da
x
&
ARK de pisagor ile
11
6
Cevap B
4
Diğer sayfaya geçiniz
LYS – 1 / GEOMETRİ DENEME ÇÖZÜMLERİ
26.
29.I. Adım : A ^- 2, 4h
A
II. Adım : A ^- 2, 4h ün x eksenine göre yansıması
B ^- 2, - 4h dir.
d
F
G
B
Deneme - 2
A noktası d doğrusu
üzerinde hareket ettirildiğinde
E
III. Adım: B ^- 2, - 4h ü orijin etrafında +270° döndürünce C ^- 4, 2h elde edilir.
C
D
-2-4
1 -2-4
&
A ^ABCh =
= 8 br 2 dir.
2 -4-2
-2-4
AG
= 2 oranı bozulmayacağı için G noktası da bir
GD
doğru boyunca hareket eder.
Cevap A
Cevap A
30. A ^- 2, m - 3, n - 4h noktası xOz düzlemine 4 birim
27. Ax 2 + Bxy + Cy 2 + Dx + Ey + F = 0 denkleminin
parabol belirtmesi için D = B 2 - 4AC = 0 olmalıdır.
uzunlukta ise
O halde, verilen denkleme göre
^a - 3h - 4 $ 1 $ 4 = 0 & a = 7 ve a = - 1 olduğundan a nın alacağı değerler toplamı
7 + ^- 1h = 6 dır.
Cevap R
m - 3 = 4 & m = 7 veya m = - 1 dir.
n - 4 = 6 & n = 10 veya n = - 2 dir.
Yukarıda bulunan m ve n değerlerine göre m + n toplamı –5 yapan ^m, nh ikilisi yoktur.
y
28.
A ^- 2, m - 3, n - 4h noktası xOy düzlemine 6 birim
uzaklıkta ise
2
Cevap A
B(0, b)
K
3
A'(−a, 0)
F'(−c, 0)
H
O
F(c, 0)
A(a, 0)
x
B'(0, −b)
2
2
y
x
+
= 1 olduğuna göre
25
16
2
2
a = 25 ve b = 16 dır.
Elips denklemi
a 2 = b 2 + c 2 & 25 = 16 + c 2 & c = " 3 bulunur.
Buna göre çemberin denklemi x 2 + y 2 = 9 dur.
&
OF = 3 br & OK = 3 br dir ve AKO da pisagor ile
&
AK = 4 br bulunur. AKO da alan eşitliği uygularsak
5 $ KH
3$4
12
bulunur.
=
& KH =
2
2
5
12
yazarsak
Çember denkleminde y yerine
5
2
9
12
m = 9 & x = " dir. K birinci bölgede
x2 +c
5
5
9 12
m olacağından koordinatlar toplamı
olduğu için K c ,
2 5
9
12
21
+
=
bulunur.
5
5
5
Cevap D
çözümler www.metinyayinlari.com da
5
Diğer sayfaya geçiniz