Zaman Uzayı Sonlu Farklar Yöntemi
Dr. Serkan Aksoy-2015
YEE Algoritması - Basit Ortam ve Kartezyen Koordinatlarda ZUSF
Maxwell denklemlerindeki diferansiyel operatörler en basit formlarına Kartezyen koordinatlarda sahip
olmaktadırlar. ZUSF yöntemi ilk kez Kartezyen koordinatlarda verildiğinden (ayrıca düzlemsel dalgaların
Kartezyen koordinatlarda kolayca ifade edilebilmesi önemli bir ayrıcalıktır), Kartezyen koordinatlarda
(
)
(
) olmak üzere, problem uzayı
(
) olacak şekilde uzayda bir
ızgara tanımlanırsa
(
)|
(
)
(
)
gösterimi temel alınabilir. Buna göre yukarıda verilen ayrıklaştırmalardan anlaşılabileceği gibi aynı ana
( ) değerlerinin hesaplanması gerekmektedir.
karşılık gelmek üzere, zamanda kayık olarak ( ) ve
( ) ve
( ) ifadelerinin
(
Bu kapsamda zamanda yarım birim kayık
) formülü gereği konumda da kayık olması gerekir. Buna göre söz konusu kayıklığın sağlandığı her bir
küçük kübik hücreye ZUSF hücresi (birim YEE hücresi) adı verilir. YEE hücresinin daha iyi anlaşılabilmesi
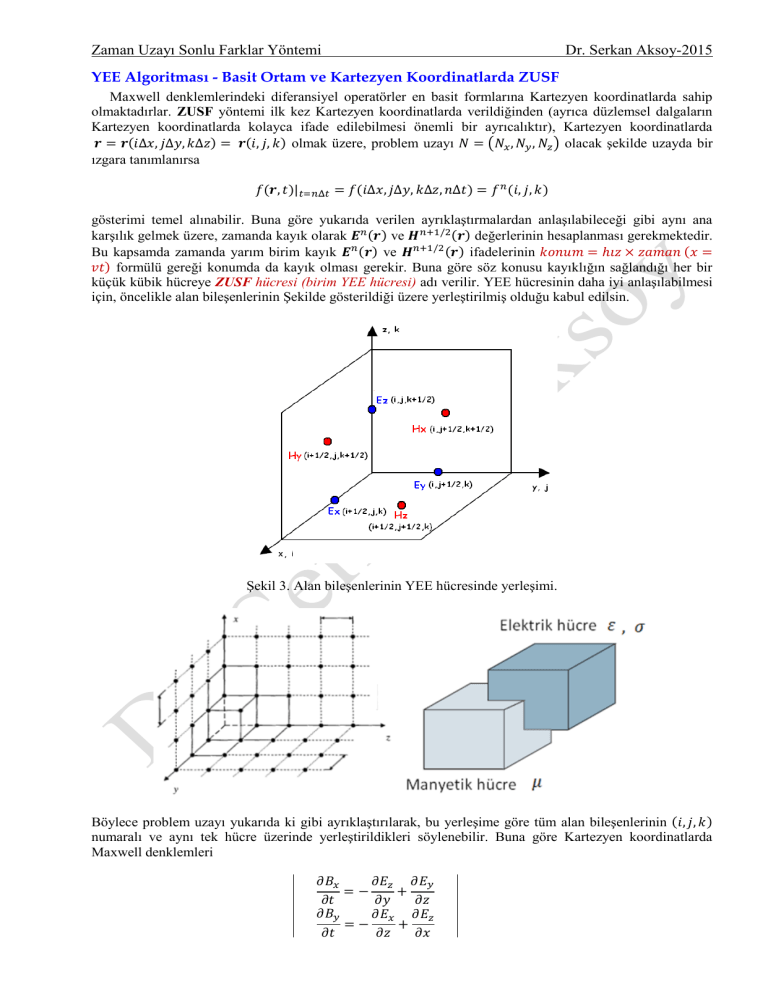
için, öncelikle alan bileşenlerinin Şekilde gösterildiği üzere yerleştirilmiş olduğu kabul edilsin.
Şekil 3. Alan bileşenlerinin YEE hücresinde yerleşimi.
)
Böylece problem uzayı yukarıda ki gibi ayrıklaştırılarak, bu yerleşime göre tüm alan bileşenlerinin (
numaralı ve aynı tek hücre üzerinde yerleştirildikleri söylenebilir. Buna göre Kartezyen koordinatlarda
Maxwell denklemleri
Zaman Uzayı Sonlu Farklar Yöntemi
Dr. Serkan Aksoy-2015
olarak yazılır. Buradan zaman adımında Şekil 3’de verilen yerleşim de göz önüne alınarak, basit ortamlar
( ) olmak üzere, güncelleme denklemleri
için, ( )
(
|
|
|
)
zamana ve konuma bağlı sayısal türevler kullanılarak
|
|
|
|
|
|
(
buradan zamanda en ileri adımda olan
)
|
çekilirse
|
|
|
|
|
|
(
)
olarak
için güncelleme denklemi elde edilir [Chu et al, 1991]. Bu çıkarımda ilk etapta
ve ’nin de
) konumunda olarak düşünüldüğü unutulmamalıdır.
ile aynı (
ve
için de aynı
teknikle güncelleme denklemleri elde edilebilir.
( ) olmak üzere, güncelleme denklemleri
Benzer biçimde basit ortamlar için ( )
(
|
|
|
|
)
zamana ve konuma bağlı sayısal türevler kullanılarak
|
|
|
|
|
|
|
(
)
bulunarak, zamanda en ileri adımda olan
|
|
|
(
|
çekilirse
|
|
|
|
)
Zaman Uzayı Sonlu Farklar Yöntemi
Dr. Serkan Aksoy-2015
için güncelleme denklemi elde edilir. Bu çıkarımda ilk etapta
ve
’nin de
ile aynı (
) konumunda olarak düşünüldüğü unutulmamalıdır.
ve
için de aynı teknikle güncelleme
denklemleri elde edilebilir.
Bilgisayar programının geliştirilerek çözülebilmesi bakımından yarım adımlık indisler tam sayılı (integer
number) indislere dönüştürülürse
olarak
|
|
|
|
(
|
(
|
|
|
|
|
|
)
|
|
)
formu elde edilir. Buna göre birim YEE hücresinde hücre içi yerleşimleri farklı olan üç elektrik ve üç
manyetik alan bileşeni bulunur. Elektrik alan bileşenleri kenar çizgilerinin ortasında iken, manyetik alan
bileşenleri hücre yüzeylerinin ortasında yerleştirilmiştir. Hücre içerisinde elektrik ve manyetik alanların
yerleşimlerindeki farklılık nedeni ile otomatik olarak zaman adımları birbirlerinden yarım zaman adımı
kadar kayık olacak şekilde farklılık gösterir. Buna göre ZUSF yönteminde, problem uzayının (
) adet birim YEE hücresinden oluştuğu düşünülür.
Birim YEE hücresinde temel mantık aynı olmakla beraber farklı biçimlerde alan bileşenleri
yerleştirilebilir. Yerleşimin aşağıdaki gibi olduğu düşünülerek
Birim YEE hücresi
bileşeni için, güncelleme denkleminin (
|
⁄
⁄
⁄
⁄
⁄
|
⁄
|
⁄
)
|
⁄
⁄
|
|
⁄
⁄
⁄
[
(
|
⁄
⁄
⁄
⁄
|
⁄
⁄
)]
biçiminde eldesi mümkündür. Elektromanyetik problemler birim YEE hücreleriyle lego olarak bilinen
oyuncaklarla bir model yapılması gibi düşünülerek çözülebilir1.
1
ZUSF güncelleme denklemlerinin indüktör-kapasitör eşdeğeri de mevcuttur [Gwarek, 1988].
Zaman Uzayı Sonlu Farklar Yöntemi
Dr. Serkan Aksoy-2015
ZUSF problem uzayının birim YEE hücresinden oluşturulması.
ZUSF yöntemi ilk kez Kartezyen koordinatlarda verilmiş olup, bu koordinat sisteminde hesap uzayının
saçıcı yüzeyinden yeterince uzak olması, birim hücrelerin en az
boyutlarında olması ve kararlılık
kriterini sağlaması gibi üç temel unsuru sağlaması gereklidir. Örneğin dördüncü denklem ele alınırsa:
[
(
)]
olarak düzenlenir. Buradan
(
|
)
⁄
⁄
olarak seçilmek üzere,
|
⁄
⁄
⁄
⁄
|
⁄
⁄
|
⁄
|
⁄
⁄
|
|
⁄
⁄
⁄
(
[
|
⁄
⁄
⁄
⁄
|
⁄
⁄
)]
halini alır. Burada tüm manyetik alan bileşenleri zaman anında hesaplanırken, soldaki ve sağdaki elektrik
alan büyüklüklerinin farklı zaman aralıklarında hesaplanması gerekmektedir. Bu durum daha fazla
algoritmik karmaşaya ve hafızaya gereksinim duyulmasına yol açacağından
|
|
⁄
⁄
⁄
⁄
olmak üzere ortalama yaklaşımı yapılırsa, ana denklem
|
⁄
⁄
⁄
|
⁄
⁄
⁄
⁄
|
⁄
⁄
⁄
Zaman Uzayı Sonlu Farklar Yöntemi
Dr. Serkan Aksoy-2015
|
⁄
|
⁄
|
⁄
|
⁄
|
⁄
⁄
⁄
⁄
|
⁄
(
⁄
⁄
⁄
⁄
⁄
|
⁄
⁄
[
)
]
olarak yazılır. Bu durumda denklem yeniden düzenlenirse
⁄
|
⁄
⁄
⁄
⁄
⁄
(
⁄
⁄
⁄
⁄
⁄
(
⁄
⁄
⁄
⁄
⁄
⁄
⁄
|
)
⁄
|
|
)
|
⁄
⁄
|
⁄
⁄
⁄
(
|
⁄
⁄
)
halini alır. Diğer alan bileşenleri için de benzer denklemler bulunabilir. İteratif denklemlerden görüldüğü gibi
uzayın her bir noktasındaki manyetik/elektrik alan bileşeni, aynı noktada bir önceki değerine ve diğer
eksenlerdeki komşu manyetik alan değerlerine bağlıdır. Ör:
değeri, kendisinin zamanda önceki değeri ile
komşu
ve
değerlerine bağlıdır. Bu denklemler ZUSF güncelleme denklemleri (update equation) adı
ile bilinir.
ve her zaman elektrik alanların bulunduğu hücre numaralarına yerleştirilmelidir. Benzer durum
manyetik geçirgenlik 'nün de her zaman manyetik alanın bulunduğu hücrelere yerleştirilmesi gerekliliğidir.
ZUSF algoritmasından görülebileceği gibi hücre başına toplamda 24 toplama ve 18 çarpma işlemi
gerekmektedir.
Burada bir diğer önemli durumda ilk katsayının sıfır veya negatif olma ihtimalinin
⁄
⁄
⁄
⁄
olacak şekilde kritik bir kayıp değerine bağlı olmasıdır. Yani uygulanacak
alamaz. Bu durumu aşmak için çözüm önerileri mevcuttur [Luebbers vd, 1995].
değeri herhangi bir değer










