7
Vektör - Kuvvet
1
5.
Test 1’in Çözümleri
A)
B)
C)
K
L
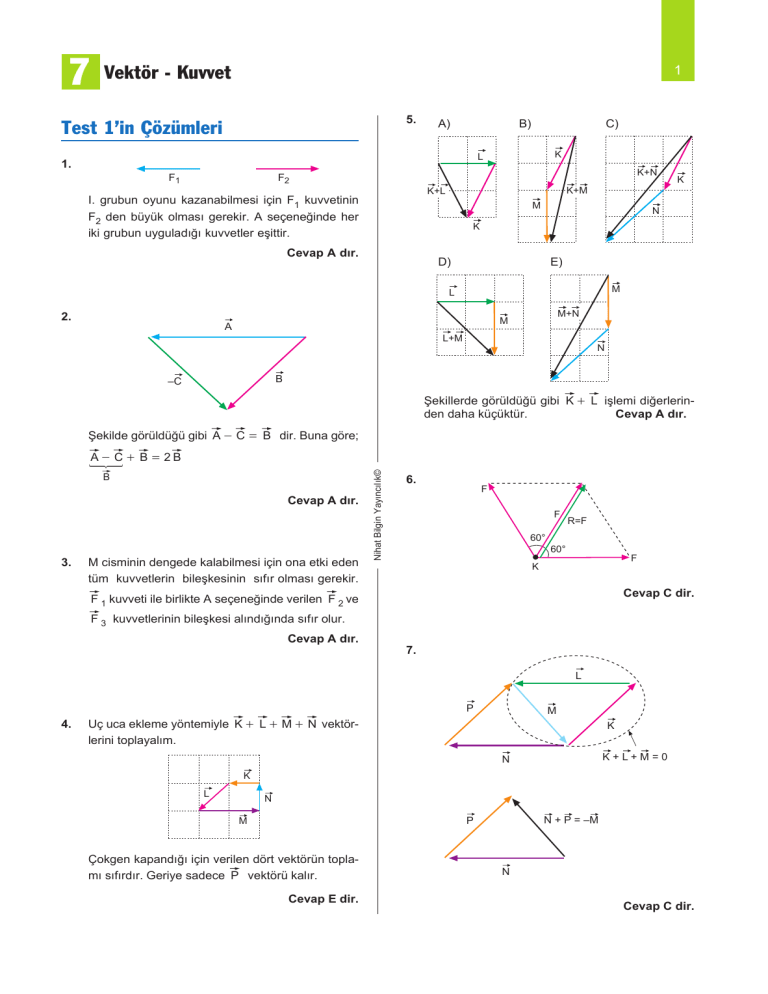
1.
F1
K+N
F2
I. grubun oyunu kazanabilmesi için F1 kuvvetinin
F2 den büyük olması gerekir. A seçeneğinde her
iki grubun uyguladığı kuvvetler eşittir.
M
N
K
Cevap A dır.
D)
E)
M
L
2.
K
K+M
K+L
M+N
M
A
L+M
N
B
–C
Şekillerde görüldüğü gibi K + L işlemi diğerlerinden daha küçüktür.
Cevap A dır.
A - C + B = 2 B
\
B
Cevap A dır.
3. M cisminin dengede kalabilmesi için ona etki eden
tüm kuvvetlerin bileşkesinin sıfır olması gerekir.
Nihat Bilgin Yayıncılık©
Şekilde görüldüğü gibi A - C = B dir. Buna göre;
6.
F
F
R=F
60°
60°
F
K
Cevap C dir.
F 1 kuvveti ile birlikte A seçeneğinde verilen F 2 ve
F 3 kuvvetlerinin bileşkesi alındığında sıfır olur.
Cevap A dır.
7.
L
P
M
4. Uç uca ekleme yöntemiyle K + L + M + N vektörlerini toplayalım.
K
K+L+M=0
N
K
L
N
N + P = –M
P
M
Çokgen kapandığı için verilen dört vektörün toplamı sıfırdır. Geriye sadece P vektörü kalır.
Cevap E dir.
N
Cevap C dir.
2
VEKTÖR - KUVVET
8.
Şekilde görüldüğü gibi bileşke kuvvet P doğrultu-
Y
sundadır.
II ve III. önermelerdeki F 1 ve F 3 kuvveti kaldırıldı-
L
ğında bileşke P doğrultusunda çıkmıyor.
–X
Cevap A dır.
K
Y–X=L+K
Verilenlerin içinde doğru olan Yalnız I dir.
12.
Cevap A dır.
R
Y
9.
X
F3
O
Bileşkenin büyüklüğü;
F1
R2 = X2 + Y2 + 2XY.cosβ
F 1 ve F 3 kuvvetleri aynı yönlü olduğundan bunların bileşkesi en büyüktür.
bağıntısı ile bulunur. β açısı küçüldükçe veya α
açısı büyüdükçe bileşke vektörünün büyüklüğü
artar.
Nihat Bilgin Yayıncılık©
Cevap B dir.
10.
Y+ Z + K + L = X
X
Y
Z
13.
L
K
Cevap B dir.
F
F
30°
30°
Y, Z, K ve L vektörleri uç uca ekli biçimde verildiğinden bunların vektörel toplamı X vektörüne eşittir. X + X = 2 X olur.
30°
120°
30°
O
R = 2F
F
F
30° 30°
F
F
120°
F
F
Cevap B dir.
Cevap B dir.
11. M cisminin P doğrultusunda hareket edebilmesi
için bileşkenin bu doğrultuda çıkması gerekir.
I.
F 2 kuvvetini kaldırıp, F 3 kuvvetini 3 katına
çıkarılım.
F1
bileşke
M
F3
P
14. F 1 ve F 2 kuvvetlerinin yerleri değiştirildiğinde bileşke kuvvetin büyüklüğü değişmez. Ancak
hareket yönü ile hareket doğrultusu değişebilir.
Hareket yönü ve doğrultusunun değişmemesi için
F 1 ve F 2 kuvvetlerinin büyüklüklerinin eşit olması gerekir. Bu yönde bir açıklama olmadığına göre
Yalnız I doğrudur.
Cevap A dır.
3
VEKTÖR - KUVVET
15.
3 br
18. F 1 + F 2 + F 3 = 0 olduğuna göre;
4 br
F2 + F3 =- F1
F1 + F3 =- F2
5 br
yazabiliriz. F 1 kuvveti ters çevrildiğinde bileşke
R 1 olmaktadır. Buna göre;
3 br
R 1 = - F 1 + F 2 + F 3 = - 2 F 1
1 44 2 44 3
- F1
O
4 br
bulunur. F 2 kuvveti ters çevrildiğinde bileşke kuvvet R 2 olmaktadır.
Biri 3 br, öteki 4 br olan iki vektör arasındaki açı
θ = 0° olsaydı bileşke 7 br olurdu. θ = 90° olsaydı bu durumda bileşke 5 br olurdu. 0° < θ < 90°
olduğuna göre, bileşke 5 ile 7 arasında bir değer
alacaktır.
R 2 = F 1 - F 2 + F 3 = - 2 F 2
| R1 |
Cevap D dir.
=
| R2 |
|2 F1 |
|2 F2 |
=
| F1 |
| F2 |
16. α > θ olduğundan bileşke kuvvet F 2 ye daha
yakın olur. Açı kuvvet ters orantı ilişkisinden yararlanarak, | F 2| > | F 1| yazabiliriz.
| R | ile | F 1| ve | R | ile | F 2| arasında kesin birşey
söylenemez.
Cevap A dır.
17.
A
F3
F1
F3
F2
–F2
F 1 + F3 = 2 F2
Şekil I
Şekil I de;
→ → →
→
F1 + F2 + F3 = 3F2
Şekil II de;
→ → → →
F1 + F3 – F2 = F2
F1 + F3 = 2 F2
Şekil II
F2
30°
F1
3α + 4α + 5α = 12α eder. 12α = 360° olduğuna
göre, α = 30° dir.
Buna göre, açılar şekilde verildiği gibidir.
A
F1
Nihat Bilgin Yayıncılık©
F3
.................. (1)
.................. (2)
(1) denkleminin (2) denklemine oranı 3 olur.
Cevap C
F2 = F1·cos30°
3
F2 = F1 ·
2
F1
2 3
2
bulunur.
=
=
F2
3
3
Cevap C dir.
VEKTÖR - KUVVET
Test 2’nin Çözümleri
5.
X + Y vektörü ile Z vektörü
X
aynı yönlü iki vektördür. Bu
3
nedenle X + Y + Z = Z
2
dir.
1. Başlangıç ile bitiş noktalarını birleştirdiğimizde
bileşke kuvvet 1 numaralı vektör olur.
X+Y
4
Y
Cevap A dır.
Z
Cevap B dir.
2. F1
K
F2x
6.
k , , , m, n, p vektörlerinin bileşkesi sıfırdır. Geriye
kalan s ve r vektörlerinin bileşkesi m kadardır.
F2
Cevap D dir.
F2
F2y
K noktasal cisminin –y yönünde hareket etmesi
için Şekil II deki 2 numaralı kuvvetin de uygulanması gerekir. Bu durumda F 2 y kalır.
Cevap B dir.
R
P+S
–P + R
P
S
–P
S
k = P + R + S = 2R
8.
60°
a
/ = –P + R + S = 2S
P - R vektörü ile S vektörü ters yönlü olduğundan
m vektörünün büyüklüğü
en küçüktür.
60°
a
a
X, Y, K, L vektörlerinin bileşkesi sıfırdır. Geriye
yalnızca Z vektörü kalır.
Cevap A dır.
R
Nihat Bilgin Yayıncılık©
3.
7.
a
a
Şekil II
P–R
P
Cevap E dir.
Şekil I
Şekil I deki üç vektörün bileşkesi sıfırdır.
–R
v3 a
Geriye kalan iki
vektörün bileşkesi
Şekil II deki gibi olup
büyüklüğü 3 a dır.
Cevap D dir.
4.
Soruda | F 1 | = 1 br, | F 2 | = 5
olarak verilmektedir. F 2 vektörü ters çevrilip şekildeki gibi
bileşke alındığında,
| F 3 | = 2 2 br bulunur. Buna
F3
–F2
göre, | F 3 | > | F 2 | > | F 1 | dir.
Cevap A dır.
F1
9.
Vektörler kaydırılarak şekildeki gibi bir köşede toplanabilir. Her üç kuvvetin bileşkesinin büyüklüğü 2F olur.
Cevap C dir.
R = 2F
F
F
60°
F
F
5
VEKTÖR - KUVVET
10. Noktasal K cismi dengede kaldığına göre, kuvvetlerin x ve y doğrultularındaki bileşenleri birbirine
eşit olmalıdır.
14. Kuvvetlerin karşılarındaki açılar aşağıdaki şekil
üzerinde verildiği gibidir.
F 1 vektörünün –y doğrultusundaki bileşeni, F 3
vektörünün +y doğrultusundaki bileşenine eşit
olmalıdır. Bu nedenle I. önerme doğru, II. ve II.
önermeler yanlıştır.
F2
F1
150°
120°
Cevap A dır.
F3
11. Bileşkenin –x yönünde F büyüklüğünde olması
için;
F1·cos37° = F
4
F1·
=F
5
5
F1 = F
4
F1·sin37° = F2
5
3
F · = F2
5
4
3
olmalıdır. Buradan F2 = F bulunur.
4
Cevap A dır.
15.
y
F3
Cevap A dır.
12. F 6 kuvveti kaldırılırsa noktasal m cismi +y yönünde hareket eder.
Cevap B dir.
Nihat Bilgin Yayıncılık©
Sinüs teoremine göre karşısındaki açısı küçük
olan kuvvet en büyüktür. Buna göre, F3 > F2 > F1
bulunur.
K
|F2|=F
|F1|=F
x
|R1,2| = v2F
F 1 ve F 2 kuvvetlerinin bileşkesinin büyüklüğü
| R 1, 2 | = 2 F dir. F 1, F 2 ve F 3 kuvvetlerinin
bileşkesinin sıfır olması için F 3 kuvvetinin büyüklüğü 2 F olması gerekir.
13. I. F 1 ve F 2 nin bileşkesi alındığında - F 3 kuvvetine eşit değildir.
F1 + F2 - 2 F3 =-3 F3
1 44 2 44 3
II. F 3 kuvvetinin ucuna F 4 kuvveti eklendiğinde
bileşkesi F 1 kuvvetini verir.
Buna göre F 1 + F 2 - 2 F 3 işleminin büyüklüğü
3 2 F bulunur.
III.
O
- F3
Cevap C dir.
16. Yay sabitleri k1, k2, k3 olan ve birbirine paralel
bağlı yayların eş değer yay sabiti;
–F2
F1
keş = k1 + k2 + k3 + ... +
biçiminde bulunur. Eğer bu yaylar birbirine seri
bağlanırsa eş değer yay sabiti;
1
1
1
1
=
+
+
k eş k 1
k2
k3
bağıntısıyla bulunur.
F1 –F2
F 1 - F 2 vektörü F 4 vektörüne eşit değildir.
Cevap B dir.
6
VEKTÖR - KUVVET
Yay sabiti k olan bir yaya büyüklüğü F olan bir
kuvvet uygulanırsa yay x kadar açılır veya sıkışır.
Yayın açılma veya sıkışma miktarı F = k·x bağıntısıyla bulunur.
öteki P kuvvet gibi yayı açıyor. Şekil III te yayın bir
ucu bağlı, öteki ucuna kuvvet uygulanıyor.
Her üç şekilde de yayı açan kuvvetler eşit olup P
kadardır. Bu nedenle x1 = x2 = x3 olur.
Cevap A dır.
Şekil I için;
keş = 3k ve F = 3k·x
Şekil II için;
keş =
yazabiliriz. Her iki şekil için F aynı olduğundan;
3k·x =
6
6
k ve F =
k·xœ
5
5
6
5
k·xœ ⇒ xœ =
x bulunur.
5
2
19.
(2+3)mgsinθ
3m
Cevap B dir.
2mgsinθ
2m
θ
Şekil I de; G1 = k·x
Şekil II de; G2 = 9k·x
G1
k·x
1
=
=
bulunur.
9k·x
9
G2
18.
1
Cevap A dır.
2
P
yay
tutuyor
yatay
P
yatay
Şekil II
Şekil I
3
2P.
sin
30°
30
°=P
yatay
Şekil III
Şekil I de yayın bir ucu bağlı, öteki ucuna P kuvveti uygulanıyor. Şekil II de P lerden biri yayı tutuyor,
Nihat Bilgin Yayıncılık©
17. Yay sabiti telin boyu ile ters orantılıdır. 3/ uzunluğundaki yayın sabiti k ise, / uzunluğundaki yayın
sabiti 3k olur. Şekil II de yaylar paralel bağlı olduğundan keş = 9k dır.
yatay
S yayının açılmasına neden olan kuvvet 5mgsini,
T yayının açılmasına neden olan kuvvet 2mgsini
dır. Özdeş yaylardan S yayı 5 birim uzarsa, T yayı
2 birim uzar.
xS
5
x T = 2 olur.
Cevap E dir.