Üç Katlı ˙Integraller

T I M U R K A R A Ç A Y- H A Y D A R E Ş - İ B R A H I M İ B R A H I M O Ğ L U
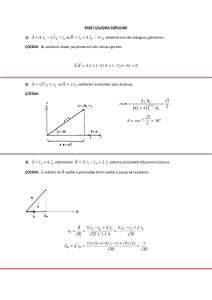
CALCULUS
S E Ç K I N YAY I N C I L I K
Copyright © 2017 Timur Karaçay-Haydar Eş-İbrahim İbrahimoğlu
B U K I TA P B A Ş K E N T Ü N I V E R S I T E S I N D E H A Z I R L A N M I Ş T I R .
ANKARA
Büyün hakları saklıdır. Yazarların izni alınmaksızın, bu kitabın tamamı vaya bir kısmı elektronik, mekanik, fotokopi veya
başka bir yolla çoğaltılamaz, kopyalanamaz, basılamaz, internet ve bilgisayar ortamında tutulamaz. Bu konuda TELİF
HAKLARI YASASI HÜKÜMLERİ geçerlidir.
Birinci baskı, Eylül 2017
Contents
Katlı İntegral
9
Hacim hesapları
33
Fiziksel uygulamalar
Üç Katlı İntegraller
Index
81
41
67
7
Cumhuriyeti kuranlara adanmıştır.
Katlı İntegral
Bu bölümde iki ve üç katlı integral uygulmlarına yer verilecektir.
Figure 1: Riemann toplamı
İki katlı İntegral
f : [a, b] ⊂ R → R, y = f (x) fonksiyonunun tek katlı integralini, Del t ax =
b − ak t ∈ [x i −1 , x i ] olmak üxere
Z
b
a
f (x)d x = lim n → ∞
n
X
f (t )∆x i
(1)
i =1
Riemann toplamının limiti olarak tanımlamıştık. f (x) ≥ 0 ise
Rb
a
f (x)d x
integrali [a, b] aralığı üzerinde ve f fonksiyonunun grafiği altında kalan
düzlemsel bölgenin alanına eşit olduğunu biliyoruz.
Şimdi, tek değişkenli fonkiyonlar için bildiğimiz bu integral kavramının
Figure 2: Riemann toplamı
f : D ⊂ R2 → R, z = f (x, y)
(2)
iki eğişkenli fonksiyonuna genelleştireceğiz. tek katlı integraldeki küçük
∆z uzunluğu yerine küçük Del t axDel y a y dikdörtgen alanı gelecektir. S
yüzeyi
S = {(x, y, z) ∈ R3 | 0 ≤ z ≤ f (x, y), (x, y) ∈ D}
(3)
f : D ⊂ R2 → R, z = f (x, y)
(4)
olsun.
Figure 3: Riemann toplamı
fonksiyonu D bölgesinde tanımlı ve her (x, y) ∈ D için | f (x, y)| ≤ M olacak
biçimde bir M sayısı var olsun. Eğer
D = {(x, y)| a ≤ x ≤ b, c ≤ y ≤ d }
(5)
ise, koordinat eksenleine paraleller çizerek, D bölgesini Şekil (13)
deki gibi sonlu sayıda küçük dikdörtgenlere ayıralım. Oluşan küçük
Figure 4: Bölüntü
dikdörtgenler ailesine D bölgesinin bir bölüntüsü (partition) denilir. Bu
bölüntüyü P ile gösterirsek;
D i j = [x i −1 , x i ] × [y j −1 , y − j ]
= {(x, y)| x i −1 ≤ x ≤ x i , y j −1 ≤ y ≤ y j }
(i = 1, 2, 3, . . . , m;
j = 1, 2, 3, . . . , n)
olur. Bölüntü aralıklarını eşit alarak,
∆x =
b−a
d −c
, ∆y =
m
n
(6)
10
CALCULUS
diyelim. D i j dikdörtgenlerinin herbirisin alanı
∆A i j = ∆x i .∆y j
(7)
dir. Bu dikdötgen alanının köşegen uzunluğuna d i j diyelim. pisagor
teoreminden, d i2j = (δx i )2 + (∆y j )2 olur.
||P || = max{d i j : (i = 1, 2, 3, . . . , m; j = 1, 2, 3, . . . , n)}
lim
m→∞,n→∞
(8)
⇒ ||P || → 0
olacaktır.
Tanım 0.1.
ve (s, t ) ∈ D i j olmak üzere
Ï
f (x, y)d A =
D
m X
n
X
lim
m→∞,n→∞
m X
n
X
= lim
f (s, t )∆A i j
i =1 j =1
||P ||→0 i =1 j =1
f (s, t )∆A i j
limiti varsa, bu limite f (x, y) fonksiyonunun D bölgesinde iki katlı
1
f (x, y) fonksiyonu D bölgesinde
sürekli ise, yukarıdaki limitler vardır.
Dolayısıyla, bir bölgede sürekli olan
iki değişkenli fonksiyonun o bölge
üzerinde iki katlı integrali vardır.
integrali denilir. 1 2 3
Süreksizlik noktalarını atarak fonksiyonun sürekli olduğu bir D bölgesinde integralini tanımlayabiliriz. D ⊂ R ve f fonksiyonu D üzerinde
sürekli olmak üzere
2
f (x, y) ≥ 0 ise z = f (x, y)
yüzeyinin altında ve D bölgesinin
üzerinde oluşan katı cismin hacmi
Ï
V=
f (x, y)d A
(9)
D
3
dır.
f (x, y) = 1 ise z = f (x, y) = 1 yüzeyinin altında ve D bölgesinin üzerinde oluşan
katı cismin hacmi V = A × 1 = A
olacağından, D bölgesinin alanı
Ï
A=
dA
(10)
D
olur.

 f (x, y) (x, y) ∈ D
F (x, y) =
0
(x, y) 6∈ D
tanımını yapalım. Buradan
Ï
Ï
f (x, y)d A =
F (x, y)d A
D
(11)
R
çıkar.
İki Katlı İntegralin Özelikleri
1.
Ï
D
2.
Ï
¡
D
α f (x, y)d A = α
¢
f (x, y) ± g (x, y d A =
Ï
(α ∈ R)
f (x, y)d A
Ï
D
(12)
Ï
f (x, y)d A ±
f (x, y)d A
(13)
D
3.
Ï
I=
=
f (x, y)d A
ÏD
D1
Ï
f (x, y)d A +
f (x, y)d A,
(D = D 1 ∪ D 2 ,
D2
D 1 ∩ D 2 = ;)
4. Her (x, y) ∈ D için f (x, y) ≤ g (x, y) ise
Ï
D
5.
Ï
f (x, y)d A ≤
g (x, y)d A
¯Ï
¯ Ï
¯
¯
¯
¯
¯
¯≤
¯g (x, y)¯ d A
f
(x,
y)d
A
¯
¯
D
(14)
D
D
Bunların ispatları iki katlı integral tanımından çıkarılabilir.
(15)
K AT L I I N T E G R A L
Ardışık İntegral
Çok katlı integral hesabı yaparken, tanımı kullanmak pratik değildir.
Onun yerine katlı integrali tek katlı integrallerin art arda uygulanması
haline dönüştürebiliriz. Bu yöntem işi çok kolaylaştırır. D bölgesi (5) gibi
verilsin. Bu durumda
Ï
D
b µZ d
Z
f (x, y)d A =
a
¶
f (x, y)d x d y
(16)
c
eşitliği vardır.
Bu eşitlikte x le y değişkenlerinin sırası değişirilebilir:
¶
Ï
Z d µZ b
f (x, y)d A =
f (x, y)d y d x
D
c
Örnek 0.2.
Ï
(17)
a
x 2 yd A
(18)
D
integralini D = {0 ≤ x ≤ 3; 1 ≤ y ≤ 2} bölgesi üzerinde bulunuz.
Çözüm 1:
Ï
x 2 yd A
D
Z 3Z 2
=
x 2 yd yd x
0 1
¶
Z 3 µZ 2
2
=
x yd y d x
I=
0
1
Z 3µ
=
x2
0
2
Z
=
1
¯2
y 2 ¯¯
dx
2 ¯ y=1
3 2
x dx
2
27
2
=
Çözüm 2:
Ï
I=
x 2 yd A
D
2Z 3
Z
x 2 yd x y
¶
Z 2 µZ 3
=
x 2 yd y d x
=
1
0
1
0
Z 2µ
y
=
1
2
Z
=
=
¯3
x 3 ¯¯
dy
3 ¯x=0
9yd y
1
27
2
Theorem 0.3.
(Fubini) f (x, y) fonksiyonu D = {a ≤ x ≤ b; c ≤ y ≤ d } bölgesi üzerinde
sürekli ise
Ï
D
Z
f (x, y)d A =
eşitliği vardır.
bZ d
a
c
d
Z
f (x, y)d yd x =
Z
b
f (x, y)d xd y
c
a
11
12
CALCULUS
Örnek 0.4. D = {1 ≤ x ≤ 2; 0 ≤ y ≤ 1} bölgesi üzerinde
Ï
x2 y 5d A
(19)
D
integralini bulunuz.
Çözüm 1:
Ï
I=
x 2 yd A
D
2 µZ 1
¶
7
x y dy dx =
18
1
0
¶
Z 1 µZ 2
7
x2 y 5d x d y =
=
18
1
0
Z
2 5
=
Örnek 0.5.
f (x, y) = 2
(20)
fonksiyonunun D = {2 ≤ x ≤ 4; 3 ≤ y ≤ 6} bölgesi üzerinden integralini
bulunuz.
Çözüm:
Z 4Z
Ï
D
2d A =
3
4
2
4
Z
2dx d y = 2
3
4d y = 8
Örnek 0.6.
f (x, y) = 6x y 2
(21)
fonksiyonunun D = {[2, 4] × [1, 2]} bölgesi üzerinden integralini bulunuz.
Çözüm 1:
Z Z
D
6x y 2 d A =
Z 4Z
2
(6x y 2 ) d y d x
1
4
Z
=
2
2
¢¯2
¡
2x y 3 ¯1 d x
4
Z
14x d x
=
1
¯4
= 7x 2 ¯2
= 84
ntegrallerin sırasını değiştirirsek,
Çözüm 2:
Z Z
D
6x y 2 d A =
Z 2Z
1
¯4
3x 2 y 2 )¯2 d x
1
4
Z
=
(6x y 2 ) d y d x
2
2¡
Z
=
4
14x36y 2 d y
1
¯2
= 12y 3 ¯1
= 84
Örnek 0.7.
f (x, y) = 2x − 4y 3
(22)
fonksiyonunun D = {[−5, 4] × [0, 3]} bölgesi üzerinden integralini bulunuz.
K AT L I I N T E G R A L
Çözüm 1:
Z Z
D
2x − 4y 3 d A =
4
Z
Z
3
−5 0
Z 4
=
Z
=
¯3
(2x y − y 4 )¯0 d x
−5
4
−5
(2x − 4y 3 ) d y d x
(6x − 1) d x
¯4
= (3x 2 − 81x)¯−5
= −756
Örnek 0.8.
f (x, y = 2 sin x − 3y 3 + 5,
(23)
fonksiyonunun D = {x 2 + y 2 ≤ 1} bölgesi üzerinden integralini bulunuz.
Çözüm:
Z
Z Z
D
34
4
Z
(2 sin x − 3y 3 + 5) d x d y
Z
Z 4
Z Z
2d A
= 34
(2 sin x) d x d y +
A
2
Z
Z 4
= 34
(−3y 3 ) d x d y
2d A =
2
2
Z Z
+
2d A
D
Z 4Z
=
4
(5) d x d y
3
2
Örnek 0.9.
f (x, y = 6x y,
(24)
fonksiyonunun A = {0 ≤ x ≤ 2; 0 ≤ y ≤ x 2 } bölgesi üzerinden integralini
bulunuz.
Çözüm 1:
x2
Z 2Z
Z Z
A
2d A =
6x yd yd x
0
2
Z
=
0
2
Z
=
0
¯x 2
(3x y 2 ¯ y=0 d x
3x 5 d x
0
1
= x 6 |20
2
1
1
= (64) − (0)
2
2
= 32
13
14
CALCULUS
Çözüm 2:
Z 2Z
Z Z
A
2d A =
0
4¡
Z
=
0
4
Z
=
0
4
Z
=
2
p
0
6x yd yd x
y
¯x 2
3x y 2 ¯ y=0 d x
¯2
3x2y ¯ y=0 d x
(12y − 3y 2 )d y
¯4
= (6y 2 − y 3 ¯0
= (6(42 ) − 43 ) − 6(02 − 02 )
= 32
Örnek 0.10.
f (x, y = y z
(25)
fonksiyonunun V = {0 ≤ y ≤ 2; −1 ≤ z ≤ y 2 ; 1 ≤ x ≤ z} bölgesi üzerinden
integralini bulunuz.
Çözüm:
Z 2Z
0
−1 y
2
z
Z
1
=
Neden İntegral sırasını değiştiriyoruz*
Katlı integrali ardışık integral (iterated) haline getirebidiğimiz durumlarda, birisini öne ya da sona almak çoğu kez önem taşımaz. ama bazı
durumlarda birisini öne almanın kolaylık sağladığı görülebilir. Bununla
ilgili iyi bilinen iki örnek verceğiz.
Örnek 0.11.
x
f (x, y) = e y
(26)
fonksiyonunun D = {1 ≤ x ≤ y; 0 ≤ y ≤ 1} bölgesi üzerinden integralini
bulunuz.
Çözüm:
Z Z
x
D
Z 1Z
e y dA=
y
x
e y dx dy
0 0
¯y
Z 1
¯
x2 ¯
=
(ye ¯ ) d y
Z
0
1
0
(e − y) d y
Z 1
= (e − 1)
yd y
0
¯1
¯
1
= (e − 1)y 2 ¯¯
2
0
1
= (e − 1)
2
R
Burada intgralin sırasını değiştirirsek xy d y integralini hesaplayamayız.
=
0
K AT L I I N T E G R A L
Örnek 0.12.
f (x, y) = e x
2
(27)
fonksiyonunun D = {0 ≤ y ≤ x; 0 ≤ x ≤ 1} bölgesi üzerinden integralini
bulunuz.
Çözüm:
Z Z
e
D
x2
x
Z 1Z
dA=
0
=
¯
2 ¯y
(ye x ¯ ) d y
0
0
1
Z
=
¯x
(yex 2 )¯0 d x
0
Z
=
0
1
Z
2
ex d y d x
1¡
¢
xex 2 d x
0
1
= (e − 1)
2
R
Burada intgralin sırasını değiştirirsek xy d y integralini hesaplayamayız.
Örnek 0.13.
f (x, y) = 6x 2 y
(28)
fonksiyonunun D = {−1 ≤ x ≤ 3; 0 ≤ y ≤ 1} bölgesi üzerinden integralini
bulunuz.
Çözüm:
3
Z
1
Z
6x 2 yd yd x
−1 0
Z
3
Z
−1
3
=
=
=
¯1
3x 2 y 2 ¯ y=0 d x
3x 2 d x
−1
¯3
x 3 ¯−1
= 28
Örnek 0.14.
f (x, y) = 6x 2 y
(29)
fonksiyonunun D = {0 ≤ x ≤ 1; −1 ≤ y ≤ 3} bölgesi üzerinden integralini
bulunuz.
Çözüm:
Z 1Z
0
3
−1
6x 2 yd xd y =
1
Z
0
1
Z
=
=
¯3
2x 3 y ¯x=−1 d y
56yd y
0
¯1
56y 2 ¯¯
2 ¯ y=0
= 28
Örnek 0.15.
f (x, y) = p
y
x + y2
(30)
fonksiyonunun D = {1 ≤ x ≤ 4; 0 ≤ y ≤ 2} bölgesi üzerinden integralini
bulunuz.
15
16
CALCULUS
Çözüm:
Z 4Z
1
2
0
y
p
x + y2
d yd x =
Z 4 ³p
1
p ´
x +4− x dx
p
p ¯¯4
= 2 ( x + 4 − x)¯
1
³p
p
p ´
p
= 2 8 − 4) − ( 5 − 1)
´
³ p
p
= 2 (2 2 − 2 − 5 + 1)
³ p
´
p
= 2 2 2− 5−1
Örnek 0.16.
f (x, y) = p
y
x + y2
(31)
fonksiyonunun D = {1 ≤ x ≤ 4; 0 ≤ y ≤ 2} bölgesi üzerinden integralini
bulunuz.
Çözüm:
Z 2Z
0
4
1
y
p
2
Z
x + y2
d xd y =
2y
0
µq
¶
q
4 + y2 − 1 + y2 d y
³ p
´
p
= 2 2 2 − 5 − 1)
Örnek 0.17.
f (x, y) = x y
(32)
fonksiyonunun D = {(x, y) : 0 ≤ 1, 0 ≤ y ≤ 3)}, bölgesi üzerinden integralini
bulunuz.
Çözüm:
Z 1Z
Z Z
=
D
x yd A =
3
x y d yd x
0
0
¯3
y 2 ¯¯
dx
2 ¯0
0
Z 1
9
=
x( − 0) d x
2
0
¯1
9 x 2 ¯¯
=
2 2 ¯0
9
=
4
Z
=
1
x
Örnek 0.18.
Figure 5: Riemann toplamı
f (x, y) =
p
xy
fonksiyonunun D = {(x, y) : 1 ≤ x ≤ 4, 4 ≤ y ≤ 9} bölgesi üzerinden
integralini bulunuz.
(33)
K AT L I I N T E G R A L
17
Çözüm:
Z 4Z
1
9p
4
Z 4Z
x y d yd x =
1
9p
4
4p
x
Z
p
y dy dx
9p
2
x
y d yd x
3 1
4
Z
¯9
2 4p
=
x(3 − 2)¯4 d x
3 1
Z
2 4p
=
x(3 − 2) d x
3 1
¯4
p
2 2
¯
= ( )( ) x 3 ¯
1
3 3
4
= ( )(8 − 1)
9
28
=
9
Z
=
Örnek 0.19.
Figure 6: Riemann toplamı
f (x, y) = ye x
(34)
fonksiyonunun D = {(x, y) : 0 ≤ x ≤ 2, −1 ≤ y ≤ 1} bölgesi üzerinden
integralini bulunuz.
Çözüm:
Z 2Z
0
Z
1
1
2
=0
Z
x
ye d x d y =
1
−1
Z
−1 0
2
¯1
y 2 ¯¯
dx
2 ¯−1
0
µ
¶Z 2
1 1
=
−
exd x
2 2 0
Z
ye x d yd x =
Z
=
−1
1
−1
ex
¯2
¯
ye ¯
x¯
dx
x=0
y(e 2 − 1)d y
¯1
y 2 ¯¯
= (e − 1) ¯
2 y=−1
µ
¶
1 1
2
= (e − 1) −
2 2
2
=0
Aşağıdaki integrallerde integral sırası önem kazanmaktadır. Hesabı
kolaylaştıran integral sırasını belirleyerek integrali hesaplayınız.
RR
xy
a) D = {(x, y) : 0 ≤ x ≤ 1, 1 ≤ y ≤ 2)},
D xe d A
Figure 7: Yüzey Altında
18
CALCULUS
Z Z
D
xe x y d A =
Z 1Z
2
xe x y d y d x
¶
Z 1 µZ 2
xy
=
x
e dy dx
0
1
0
=
1
1¡
Z
e
2x
0
2x
¢
− ex d x
¯1
¯
=
−e ¯
2
0
µ 2
¶ µ
¶
e
1
=
−e −
−1
2
2
e
x¯
1
e2
−e +
2
2
RR
x
b)D = {(x, y) : 0 ≤ x ≤ 1, 0 ≤ y ≤ 1},
D 1+x y d A}
=
u = 1 + x y, d u = xd y konumuyla;
Figure 8: Bölüntü
Z Z
D
x
dA=
1+xy
1
Z
¯1
l n(1 + x y)¯0 d x
0
1
Z
=
[l n(1 + x) − l n1]d x
0
1
Z
=
l n(1 + x)d x
0
= (x + 1) (l n(x + 1) − l n1)|10
= 2(l n2 − 1)
Verilen denklemlerin grafikleri ile sınırlanan bölgeyi grafikle gösteriniz
ve küme gösterimiyle, düzgün x-bölgesi ve/veya düzgün y-bölgesi olarak
ifade ediniz.
Figure 9: Bölüntü
a) y = 5 − x 2 , y = 1
D = {(x, y)| − 2 ≤ x ≤ 2,
= {(x, y)|1 ≤ y ≤ 5,
1 ≤ y ≤ 5 − x2}
p
p
− 5 − y ≤ x ≤ 5 − y}
b) y = x 2 , y = 4
Figure 10: Yüzey Altında Hacim
D = {(x, y)| − 2 ≤ x ≤ 2,
= {(x, y)|0 ≤ y ≤ 4,
x 2 ≤ y ≤ 4}
p
p
− y ≤ x ≤ y}
c) y = x 2 − 6x + 8, x + y = 8
D = {(x, y)|y = x 2 − 6x + 8, x + y = 8}
d) y = 5 + 4x − x 2 , x + y = 5
Figure 11: Sütünların Oluşumu
D = {(x, y)|0 ≤ x ≤ 5,
−x + 5 ≤ y ≤ 5 + 4x − x 2 }
K AT L I I N T E G R A L
19
Köşeleri (1, 1), (3, 3), (4, 3) ve (5, 2) noktalarında olan dörtgensel bölge
D olsun. D yi sadece sınır noktalarında ortak noktaları bulunan düzgün
bölgelerin birleşimi olarak ifade ederek
RR
a) D 24xd A
D = D! ∪ D2 ∪ D3
Z Z
Z Z
D
24xd A =
Z Z
D
24xd A 1 +
Z 4Z
+
Z 5Z
+
Z Z
24xd yd x
7−x
24xd yd x
x 3
4+4
4
Z Z
D
24yd A =
Z Z
D
Z 3Z
=
Z 4Z
+
Z 5Z
D
24yd A 2 +
D3
24yd A 3
24yd yd x
3
24yd yd x
7−x
x 3
4+4
4
Z Z
x
x 3
4+4
3
+
24yd A 1 +
x 3
4+4
1
mann toplamı
24xd A 3
3
x 3
4+4
3
D
24xd yd x
x 3
4+4
1
D
x
Z 3Z
=
Z Z
24xd A 2 +
24yd yd x
İntegrasyon bölgesi verilmiş olan çift katlı integrali hesaplayınız.
RR
2
a) D = {(x, y) : 0 ≤ y ≤ 2x, 0 ≤ x ≤ 2},
D (x + x y)d A
Z 2Z
0
2x
0
(x 2 + x y)d yd x = 16
RR
b) D = {(x, y) : 0 ≤ x <≤ y, 0 ≤ y ≤ 1},
y
Z 1Z
0
0
24x y 3 d xd y =
D (24x y
1
Z
0
1
Z
=
0
1
Z
=
Figure 15: Riemann toplamı
3
)d A
¯y
12x 2 y 3 ¯0 d y
12y 3 (y 2 − 0)d y
Figure 16: Riemann toplamı
12y 5 d y
0
¯1
= 2y 6 ¯0
=2
c) D = {(x, y) : y 2 ≤ x ≤ y, 0 ≤ y ≤ 1},
Z 1Z
0
y
y2
p
RR p
D
x yd xd y =
ç) D = {(x, y) : 0 ≤ x ≤ y 2 , 0 ≤ y ≤ 1},
RR
D
x yd A
2
27
Figure 17: Riemann toplamı
ye x d A
Figure 18: Riemann toplamı
20
CALCULUS
x
Z 1Z
0
0
ye x d xd y =
1
Z
¯y 2
e x y ¯x=0 d y
0
1
Z
=
0
2
(e y y − y)d y
¯1
1 y 2 y 2 ¯¯
= e − ¯
2
2 0
1
= e −1
2
d) D = {(x, y) : 0 ≤ y ≤ x, 0 ≤ x ≤ 1},
Figure 19: Riemann toplamı
x
Z 1Z
0
0
e x+y d yd x =
RR
De
x
Z 1Z
0
x+y
dA
e x e y d yd x
0
1
= (e − 1)2
2
İntegrasyon bölgesinin grafiğini çizerek integral sırasını değiştiriniz.
R 1 R x3
a) 0 x 4 f (x, y)d yd x
Figure 20: Riemann toplamı
Z 1Z
0
x3
x4
f (x, y)d yd x
p
4
Z 1Z
=
p
3
0
y
f (x, y)d xd y
y
Aşağıdaki integralleri integrai sırasını değiştirerek hesaplayınız (integral sırasını değiştirmeden hesaplamayı denemeyiniz!)
a)
Z 1Z
0
1
x
2
e y d yd x =
y
Z 1Z
0
=
0
1
Z
¯
2 ¯y
e y x¯ d y
0
0
1
Z
2
e y d xd y
y2
ye d y
¯
2 y
e y ¯¯
=
¯
2 ¯
=
0
0
e 1
= −
2 2
1
= (e − 1)
2
Figure 21: Riemann toplamı
K AT L I I N T E G R A L
21
b)
Z 1Z
1
y2
0
p
Z 1Z
x2
12ye d xd y =
0
2
12ye x d yd x
0
0
¯p x
¯
12e ¯
dx
Z
1
1
Z
=
x
x2 ¯
y=0
x2
e xd x
¯
2 ¯1
= 3e x ¯
=6
0
x=0
= 3(e − 1)
c)
Z 2Z
4
4y
d xd y =
1 + x2
x
4y
d yd x
1 + x2
¯p x
Z 4
¯
1
2¯
=
2y ¯ d x
2
0 1+x
0
p
Z 4
2 ¯¯ x
2y ¯
=
dx
2¯
0 1+x 0
Z 4
2x
=
dx
1
+
x2
0
¯4
= l n(1 + x 2 )¯
y2
0
p
Z 4Z
0
Figure 22: Riemann toplamı
0
0
= l n(17) − l n(1)
= l n(17)
ç)
Z 4Z
0
2
x
2
2
q
1 + 2y 2 d yd x =
Z 2Z
2
0
=
=
=
=
b)
R 1 R y2
0
0
0
2
Z
2
=
=
2y
q
0
q
1 + 2y 2 d xd y
Figure 23: Riemann toplamı
¯2y
¯
1 + 2y 2 x ¯¯ d y
0
Z 2q
1 + 2y 2 4yd y
¯2
q
¯
2
(1 + 2y 2 )3 ¯¯
3
0
´
2 ³p 3
9 −1
3
2
(26)
3
52
3
0
f (x, y)d xd y
Figure 24: Riemann toplamı
y2
Z 1Z
f (x, y)d xd y
0
0
Z 1Z
=
c)
R 2 R 4x
0
x3
0
1
p
f (x, y)d yd x
x
f (x, y)d yd x
Figure 25: Riemann toplamı
22
CALCULUS
Z 2Z
4x
f (x, y)d xd y
x3
0
p
3
Z 8Z
q
ç)
Figure 27: Riemann toplamı
R8R
0
y
4
y
2
y
f (x, y)d yd x
=
y/4
0
f (x, y)d yd x
q
Z 8Z
0
y
2
f (x, y)d xd y
y/4
Z 2Z
=
4x
f (x, y)d yd x
2x 2
0
İntegrasyon bölgesi D verilen denklemlerin grafikleri ile sınırlanan çift
katlı integrali hesaplayınız.
a) D = {y = x 2 , y = x} ile sınırlı,
Z Z
D
y 2d A
RR
D
y 2d A =
x2
Z 1Z
x3
0
=
¯x 2
y 3 ¯¯
dx
3 ¯x 3
1
Z
0
1
=
3
y 2 d yd x
1
Z
0
(x 6 − x 9 )d x
¯1
1 x 7 x 10 ¯¯
= [ −
]
3 7
10 ¯0
1
=
70
RR
2
2
2
b) D = {y = 2x, y = 8 − 2x ile sınırlı },
D (4 − y )d A
Figure 28: Riemann toplamı
Z Z
D
(4 − y 2 )d A = 2
Z 2Z
p
2x
0
(4 − y 2 )d yd x
0
p
4 Z 8−2x
Z
(4 − y 2 )d yd x
µ
¶
128 128
=2
+
15
15
512
=
15
+2
Z Z
Figure 29: Riemann toplamı
2
D
ex d A =
2
x/2
Z 2Z
0
2
Z
0
2
¯x/2
2 ¯
e x y ¯¯ d x
0
e
0
2
e x d yd x
0
Z
=
=
0
x2
x
dx
2
Z
1 2 x2
xe d x
2 0
1
= (e 4 − 1)
4
=
K AT L I I N T E G R A L
ç) D = {x = 0, x = 2y, y = 1} ile sınırlı bölge,
Z Z
y
D
e− 2 d A =
Z 2Z
De
y
−2
dA
y
e − 2 d yd x
x/2
0
2
Z
=
1
RR
−2e
0
¯1
¯
¯ dx
−y/2 ¯
x/2
2
µZ
e
= −2
−1/2
0
2
µZ
xe
= −2
−e
−1/2
0
−x/4
+ 4e
¶
dx
−x/2
·
4
2
= −2 ( p + ) − (0 + 4)
e e
8
4
= 8− p −
e e
p
8e − 4 e − 8
=
e
¶2
dx
¸0
Katlı İntegral Uygulamaları
Theorem 0.20. D = {a ≤ x ≤ b; g 1 (x) ≤ y ≤ g 2 (x)} bölgesi üzerinde f (x, y)
fonksiyonu sürekli ise
Ï
D
b Z g 2 (x)
Z
f (x, y)d A =
f (x, y)d yd x
a
g 1 (x)
olur.
Değişkenlerin yerleri değiştirilirse, benzer sonuç elde edilebilir:
D = {c ≤ y ≤ d ; h 1 (y) ≤ y ≤ h 2 (y)} bölgesi üzerinde f (x, y) fonksiyonu
sürekli ise
Ï
D
d
Z
f (x, y)d A =
h 2 (x)
Z
f (x, y)d xd y
c
h 1 (x)
olur.
İspat: Ardışık integral tanımından çıkarılır.
Örnek 0.21. D = {y = 0, Y = 2x, x = 1} doğruları ile sınırlı bölge ise
Ï
(x + y)d A
D
integralini bulunuz.
Çözüm :
Ï
I=
(x + y)d A
D
1 µZ 2x
¶
4
(x + y)d y d x =
3
0
0
!
Z 2 ÃZ 1
4
=
(x + y)d x d y =
y
3
0
2
Z
=
Örnek 0.22.
ex
Z 2Z
I=
f (x, y)d yd x
0
1
integralinin ardışık integral sırasını değiştiriniz.
(35)
23
24
CALCULUS
Çözüm :
e2 Z 2
Z
I=
f (x, y)d xd y
lny
1
Örnek 0.23.
Z
I=
2
x
Z
−1 x 2 −2
f (x, y)d yd x
integralinin ardışık integral sırasını değiştiriniz.
Çözüm :
Z
I=
−1 Z
−2
p
y+2
p
−
Z
y+2
f (x, y)d yd x +
2
Z p y+2
f (x, y)d yd x
−1 y
Örnek 0.24.
Z 1Z
I=
1
2
e y d yd x
x
0
integralini hesaplayınız..
Çözüm :
y
Z 1Z
I=
0
=
0
1
Z
2
e y d xd y
2
ye y d y
0
e −1
2
=
Örnek 0.25.
x2
Z 1Z
I=
0
(x + y)d yd x
0
integralinin ardışık integral sırasını değiştirerek hesaplayınız.
Çözüm :
Z 1Z
I=
=
0
1
p
y
(x + y)d xd y
7
20
Örnek 0.26. D bölgesi x 2 + y 2 = 1 çemberi ile x 2 + 2y 2 = 1 elipsi ile sınırlı
bölge ise
Ï
I=
x2d A
D
integralini hesaplayınız.
Çözüm : şekilden görüldüğü gibi D = D 1 ∪ D 2 olarak iki parçaya
K AT L I I N T E G R A L
ayırmalıyız.
Ï
Ï
I=
x2d A =
D
1
Z
=
D1
Z
1−x 2
2
−1
Z
=2
p
1−x 2
q
1
−1
x2d A +
x 2 d yd x +

s
p
x2  1 − x2 −
Z
Ï
x2d A
D2
q
2
Z
1
− 1−x
2
p
−1 − 1−x 2
x 2 d yd x

1 − x2 
dx
2
µ
¶Z 1 p
1
= 2 1− p
x2 1 − x2d x
2 −1
µ
¶Z 1 p
1
= 4 1− p
x 2 1 − x 2 d x,
(x = si nt , d x = cost d t )
2 −1
µ
¶ Z π/2
1
= 4 1− p
si n 2 t cos 2 t d t
2 0
µ
¶ Z
1 1 π/2
= 4 1− p
si n 2 2t d t
2 4 0
¶ Z
µ
1 1 π/2
(1 − cos4t )d t
= 4 1− p
2 8 0
¯
µ
¶ µ
1 1
si n4t ¯¯π/2
= 4 1− p
t−
4 ¯0
2 8
µ
¶
1 π
= 4 1− p
2 16
p
( 2 − 1)π
=
p
4 2
Örnek 0.27. D bölgesi birinci dörtte birlik alanda x y = 16, y = x, y = 0, x =
8 eğrileri ile sınırlı bölge ise
Ï
I=
x2d A
D
integralini hesaplayınız.
Çözüm 1:
Ï
I=
D
4 Z 16/y
Z
=
x2d A =
y
2
1
=
3
Z 4µ
2
Ï
D1
x2d A +
x 2 d xd y +
Ï
x2d A
D2
Z 2Z
8
x 2 d xd y
y
0
¶
Z
1 2 3
163
dy +
(8 − y 3 )d y
y3
3 0
= 448
Çözüm 2:
Ï
I=
D
4Z x
Z
=
x2d A =
0
0
Ï
D1
x2d A +
x 2 d yd x +
Z 8Z
4
Ï
16/x
x2d A
D2
x 2 d yd x
0
= 448
Örnek 0.28. D bölgesi y = x 2 , y = 8 − x 2 eğrileri ile sınırlı bölgenin alanını
bulunuz.
Ï
Al an A =
dA
D
25
26
CALCULUS
integralini hesaplayınız.
Çözüm 1:
Ï
I=
D
Z
=
Z
=
2
Ï
x2d A =
Z
Ï
x2d A
D2
8−x 2
d yd x
−2 x 2
2¡
−2
D1
x2d A +
¢
(8 − x 2 ) − x 2 d x
64
=
3
Alıştırmalar
Aşağıdaki katlı hesaplayınız.
Z 1Z
1−x
(1 − x − y)d yd x
1.
0
0
Z 1Z
2.
1
cos y 3 d yd x
p
0
x
1
Z 1Z
sin x 2 d xd y
3.
y
0
Z 2Z
p
2x−x 2
4.
0
0
Z 4Z
2y
5.
y
0
2
Z
(x 2 + y 2 )d yd x
(x + e y )d xd y
x 2 +1
Z
(x y)d yd x
6.
−1 x
Z 1/2 Z y
7.
0
0
p
x
Z 4Z
1
d xd y
p
1 − x2
x 2 yd yd x
Z p2 Z p2−y 2
(2x − y)d xd y
9.
p
8.
0
x/2
0
−
Z 1Z
2y
10.
0
Z 1Z
11.
0
0
2−y 2
2
e −y d xd y
p
1−x 2
p
− 1−x 2
xd yd x
Z 1 Z p1−y 2
xd xd y
12.
−1 0
Katlı integralde değişken değiştirme
Tek değişkenlilerde olduğu gibi, bazı durumlarda değişken değiştirerek
katlı integral daha kolay hesaplanabilir hale dönüştürülebilir. Aslında
katlı integrali ardışık integraller olarak hesaplayabildiğinmize göre,
değişken değiştirimi tek değişkenli integrallerde yaptığımızın tekrarı
olacaktır. Yine de bu dönüşümün yapılabilmesini mümkün kılan teoremi
ifade etmekte yarar vardır.
K AT L I I N T E G R A L
Theorem 0.29. 1. f (x, y) fonksiyonu xy-düzlemindeki bir D bölgesinde
sürekli olsun.
2. Düzlemde tanımlı bir T dönüşümü
T:

x = g (u, v)
 y = h(u, v)
parametrik biçiminde verilsin.
3. g ve h fonksiyonları D ∗ üzerinde sürekli olsunlar.
4. T dönüşümü bire-bir örten olacak biçimde D bölgesini D ∗ bölgesine
dönüştürsün.
5.
∂(x, y)
J (u, v) =
=
∂(u, v)
"
∂x
∂u
∂y
∂u
∂x
∂v
∂y
∂v
#
(36)
6. J (u, v) 6= 0
varsayıları sağlanıyorsa
Ï
Ï
D
f (x, y)d yd x =
D∗
¡
¢
f g (u, v), h(u, v) |J (u, v)| d ud v
(37)
dir.
İspat: T dönüşümü uv-düzlemindeki bir (u, v) noktasını xy-düzlemindeki
(x, y) noktasına götüren dönüşümdür. g , h fonksiyonları D ∗ bölgesinde
tanımlı ve sürekli türevlere sahip fonksiyonlardır. T dönüşümünü vektör
değerli bir fonksiyon imiş gibi düşünebiliriz. (0, 0) baş noktasını (x, y)
noktasına birleştiren vektörü ~
r = x~
i + y~
j ya da ~
r = g (u, v)~
i + h(u, v)~
j
biçiminde yazabilirz. g , h fonksiyonları süreli türevlere sahip olduğuna
göre
∂g ∂g ∂h ∂h
∂u , ∂v , ∂u , ∂v
kısmi türevleri var ve süreklidirler. u = u 0 ve v = v 0
eğrileinin teğet vektörleri
r
∂~
r ∂~
∂v ∂u
olacaktır.
T dönüşümü altında boyutları ∆u × ∆v olan dikdörtgen xy-düzleminde
biçemi bozulmuş dikdörtgenimsi bir bölgeye dönüşür. Bunun alanı
yaklaşık olarak,
¯
¯
¯ ∂~
r ¯¯
¯ r × ∂~
¯ ∂u ∂v ¯ ∆u∆v
olur. Ayrıca,

i
¯
¯
¯ ∂~
r ¯¯  ∂x
¯ r × ∂~
¯ ∂u ∂v ¯ =  ∂u
∂x
∂v
j
∂y
∂u
∂y
∂v
k


0 = k
0
"
∂x
∂u
∂v
∂u
∂y
∂u
∂y
∂v
#
¯
¯
¯ ∂(x, y) ¯
¯
¯
=k¯
∂(u, v) ¯
olur. Buradan,
¯
¯
¯
¯
¯ ∂~
¯ ∂(x, y) ¯
r ¯¯
¯ r × ∂~
¯
¯
¯ ∂u ∂v ¯ ∆u∆v = ¯ ∂(u, v) ¯ ∆u∆v
elde edilir. Şimdi integral tanımına dönersek,
X ¡
¢
f g (u, v), h(u, v) |J (u, v)| d ud v
27
28
CALCULUS
toplamının limiti varsa, bu limit
Ï
f (x, y)d yd x
D
integraline eşit olacaktır. O halde,
Ï
Ï
¡
¢
f (x, y)d yd x =
f g (u, v), h(u, v) |J (u, v)| d ud v
D∗
D
(38)
çıkar. Simgelerde birliği sağlamak için,
d A = d xd y

i
j
 ∂x ∂y
=  ∂u ∂u
∂y
∂v
k


0
∂x
0
∂v
¯
¯
¯ ∂(x, y) ¯
¯ d ud v
= ¯¯
∂(u, v) ¯
olduğunu vurgulamak yeterlidir.
Örnek 0.30.
x2
a2
y2
+ b 2 ≤ 1 ile sınırlı D bölgesinin alanını değişken değiştirme
yöntemi ile bulunuz.
Çözüm:x = au, y = bv değişken değiştirimini yaparsak, D bölgesi
2
u + v 2 ≤ 1 açık diskine dönüşür. Bunu yapan parametrik dönüşümler
sürekli türevlenebilir. Dolayısıyla Teorem (36) uygulanabilir. ( a > 0, b > 0
olmak üzere
¯"
¯
¯
¯
¯ ∂(x, y) ¯
¯ d ud v = ¯¯ a
d xd y = ¯¯
¯
¯ 0
∂(u, v)
olur. Dolayısıyla,
Ï
D
Ï
1 d xd y =
D∗
#¯
0 ¯¯
¯ = ab d ud v
b ¯
ab d ud v = ab(π12 ) = πab
çıkar.
Örnek 0.31. Köşeleri (0, 0), (1, 1), (2, 0) olan D üçgeninin üzerinde,
Ï
(x + y)3 d xd y
D
integralini değişken drğiştirimi yaparak bulunuz.
Çözüm:u = y − x, v = y + x değişken değiştirimini yaparsak, D bölgesi
köşeleri (0, 0), (0, 2), (−2, 2) olan D ∗ üçgenine dönüşür. Bunu yapan
parametrik dönüşümler sürekli türevlenebilir. Dolayısıyla Teorem (36)
uygulanabilir.
∂(u, v)
=
∂(x, y)
dir. Buradan,
1
∂(x,y)
∂(u,v)
"
=
−1
1
1
1
#
= −2
¯
¯
¯ ∂(x, y) ¯
¯ d ud v = 1 d ud v
d xd y = ¯¯
∂(u, v) ¯
2
Ï
Ï
1 3
(x + y)3 d xd y =
v d ud v
∗
D
D 2
Z 2Z
1
=
−v 0 v 3 d ud v
2 0
Z
1 2 4
=
v dv
2 0
16
=
5
K AT L I I N T E G R A L
Örnek 0.32. Köşeleri (0, 0), (1, 1), (2, 0) olan D üçgeninin üzerinde,
Ï y−x
e y+x d xd y
D
integralini değişken drğiştirimi yaparak bulunuz.
Çözüm:u = y − x, v = y + x ⇒ x = 21 (u + v), y = 12 (v − u ⇒ u =
v, u = −v, v = 2) değişken değiştirimini yaparsak, D bölgesi köşeleri
(0, 0), (2, 2), (−2, 2) olan D ∗ üçgenine dönüşür. Bunu yapan parametrik
dönüşümler sürekli türevlenebilir. Dolayısıyla Teorem (36) uygulanabilir.
¯
¯ " 1
¯ ∂(x, y) ¯
−2
¯
¯
¯ ∂(u, v) ¯ = 1
2
1
2
1
2
#
=−
1
2
olur. Buradan,
Ï
Ï
y−x
D
e y+x d xd y =
u
e v d ud v
D∗
Z Z
1 2 v u
=
e v d ud v
2 0 −v
Z
e − 1e 2
v dv
=
2
0
1
=e−
e
Alıştırmalar
1. Köşeleri (1, 0), (2, 0), (0, −2), (0, −1) olan D yamuğu üzerinde,
Ï y−x
e y+x d xd y
D
integralini bulunuz.
2. x − 2y = 0, x − 2y = 4, 3x − y = 1, 3x − y = 8 doğrularının sınırladığıD
bölgesi üzerinde,
i i nt D
x − 2y
dA
3x − y
integralini hesaplayınız.
3. Köşeleri (1, 0), (2, 0), (0, 2), (0, 1) olan D yamuğu üzerinde,
µ
¶
Ï
y −x
dA
cos
y +x
D
integralini hesaplayınız.
4. D = {(x, y) :
π < x + y < 2π, −π < x − y < π} bölgesi üzerinden,
i i nt D (x 2 − y 2 ) sin2 (x + y) d xd y
integralini hesaplayınız.
5. 9x 2 + 4y 2 = 1 elipsi üzerinden,
Ï
sin(9x 2 + 4y 2 )d A
D
integralini hesaplayınız.
29
30
CALCULUS
6. |x| + |y| ≤ 1 eitsizliği ile belirlenen D bölgesi üzerinden,
Ï
e x+y d A
D
integralini hesaplayınız.
7. Köşeleri (0, 0), (2π, 0), (0, π) olan D üçgeni üzerinden,
Ï
D
sin(x + 2y). cos(x − 2y)d A
integralini hesaplayınız.
8. y = x 2 , y = 4x 2 , x y = 1, x y = 5 eğrilerinin sınırladığı D bölgesi üzerinden,
Ï
x yd A
D
integralini hesaplayınız.
İki Katlı İntegral İle Düzlemsel Alan Hesabı
1. Pappus teoremini kullanarak dik dairesel koninin yanal yüzeyinin
alanını ve hacmini bulunuz.
Çözüm:
Genel olması için koninin yüksekliği olarak herhangi bir r sayısı alalım.
Koninin simetri doğrusu O y− ekseni olacak şekilde tepe noktasını
(O,O) başlangıç noktasına koyalım. Koni şekilde görüldüğü gibi baş
aşağı konumlanmış olsun.
Koninin yanal yüzeyindeki |OB | doğru parçasını kütle merkezi, |OB |
bin orta noktasıdır: (x, y) = ( 12 r , 21 h) dir (bkz. ). Alan
A = |OB |.2πR = 2
p
= πr r 2 + h 2
p
r 2 + h 2 .π
r
2
O AB üçgeninin kütle merkezi ( r3 , h2 ) dır. Hacim
V = (2πR)
rh
r rh 1 2
= 2i .
= πr h
2
3 2
3
olur.
2. Pappus’un ikinci teoremini kullanarak y =
p
r 2 − x 2 , −r ≤ x ≤ r
yayının kütle merkezini bulunuz.
Çözüm:
Pappus’un ikinci teoremini kullanacağız. Kürenin lanının 4πr
olduğunu biliyouz. Buna göre;
x = 0,
(39)
K AT L I I N T E G R A L
R
y=
31
ỹd m
yd m
Rp
p
r 2 − x 2 . −t 1 + y 2 d x
=
ds
Rp
r 2 − x2. p 2 r 2
r −x d x
R
=
p r
dx
r 2 −x 2
Rr
rdx
= R r −r r
p
dx
−r
2
2
r −x
2r 2
=
πr
2r
=
π
Yüzey Alanı S:
S = (r π)2π(
2r π
= 4πr 2
)
(40)
çıkar. Buunu daha kısa yolla yapabiliriz.
4πr 2 = (r π)2πy
⇒y=
2
r
π
Verilen iki denklemin grafikleri arasında kalan bölgenin alanını çift
katlı integralle hesaplayınız.
a) y =
x2
4 ,y
= 21 x + 2
Z
Al an =
4
Z
2+x/2
−2 x 2 /4
Z 4µ
x
d yd x
Figure 30: Soru7-11a
¶
x2
=
+2−
dx
4
−2 2
64
8
= (4 + 8 − ) ∗ (1 − 4 + )
8
12
= 15 − 6
=9
b) x y = 5, x + y = 6
Z 5Z
Al an =
6−x
d yd x
1
5/x
¶
Z 5µ
5
=
(6 − x) −
dx
x
1
¯5
¯
x2
= (6 −
− 5l n(x))¯¯ )
2
1
25
1
= (30 −
− 5l n5) − (6 − − 5l n1)
2
2
= 30 − 18 − 5l n5
= 12 − 5l n5
=9
Figure 31: x y = 5, x + y = 6
32
CALCULUS
c) y = x, y = x 3
Z 1Z
Al an = 2
x3
0
d yd x
1¡
Z
=2
x
0
¢
(x − x 3 ) d x
x2 x4
−
2
4
1 1
= 2( − )
2 4
1
=
2
µ
¶1
=2
0
Örnek
r yarıçaplı bir çember, çember düzleminde ve çember merkezine
b, (b > r ) uzaklıkta sabit duran bir eksen etrafında döndürülüyor. Meydana gelen cismin (simit, torus, daughnut) yüzey alanını ve hacmini
bulunuz.
Çözüm:
Çemberin ağırlık merkezi kendi merkezidir. Çemberin merkezi eksen
etrafında bir dönüş yapınca 2πb kadar yol alır. Çemberin alanı πr 2 dir.
Pappus teoremine göre hacim
V = (2πb)(πr 2 ) = 2π2 br 2
olur, yüzey alanı ise
S = (2πb)(2πr ) = 4π2 br
olur.
Alıştırmalar
1. x = a, y = a karesinden a yarıçaplı çember çıkarılıyor. Geri kalan
düzlemsel bölgenin alanını bulınız.
Hacim hesapları
Aşağıda tanımlanan hacimleri hesaplayınız (Sadece D bölgesinin
grafiğini çiziniz).
a) Köşeleri (0,0), (0,1), (1,0) olan D üçgeni ile z = x + y nin grafiği
arasındaki hacim,
Z Z
V=
D
(x + y)d A
Z 1Z
=
0
0
(x + y)d yd x
1
Z
=
1−x
0
(x y +
¯1−x
y 2 ¯¯
dx
2 ¯ y=0
¸
(1 − x)2
=
dx
x(1 − x) +
2
0
¸
Z 1· 2
−x
1
=
dx
+
2
2
0
¯1
−x 3 x ¯¯
=
+ ¯
6
2 0
1 1
=− +
6 2
4
=
12
1
=
3
Z 1·
Figure 33: Köşeleri:(0, 0), (0, 1), (1, 0)
34
CALCULUS
b) Köşeleri (0,0), (0,2), (2,2) olan D üçgeni ile z = (x − y)2 nin grafiği
arasındaki hacim,
Z Z
V=
D
(x − y)2 d A
Z 2Z
=
=
Figure 34: Köşeleri: (0, 0), (0, 2), (2, 2)
0
2−x
0
(x − y)2 d yd x
4
3
Hacim Hesapları
y = l − x 2 ve y = 0 ile sınırlanan D bölgesi ile z = 4 düzlemi arasında kalan
hacim.
Figure 35: Köşeleri: y = 1 − x 2 , y = 0, z = 4
Z Z
V=
4d A
D
Z
=
1−x 2
4d yd x
Z
=
Z
−1 0
Z 1
=
=
1
−1
1
−1
Z 1
−1
¯1−x 2
4y ¯ y=0 d x
4(1 − x 2 )d x
(4 − 4x 2 )d x
¯1
4x 3 ¯¯
= 2(4x −
3 ¯0
16
=
3
Dönel Cisimleri Hacimlerin
Düzlemsel bir R bölgesinin, kendisini kesmeyen bir doğru etrafında
dönmesiyle oluşan cisme dönel katı cisim denilir. Bu cisim gerçekte
uxayda var olmayan ama hayal ettiğimiz bir cisimdir.
Düzlemsel R bölgesinin D doğrusuna göre üst sınırı f (x) fonksiyonu
ile belirlensin. R bölgesinin her noktasından onu kesmeyen D doğrusuna
dikmeler inelim. R bölgesi parçalı değilse, dikmelerin ayakları D doğrusu
üzerinde bir [a, b] aralığı oluşturur. D doğrusunu koordinat ekseni olarak
alırsak, [a, b] aralığı f fonksiyonunun tanım bölgesi içinde olacaktır.
Dikmelerin ayaklarını içeren [a, b] aralığının bir bölüntüsünü (partition)
P ile gösterelim:
a = x 0 < x 1 < −x 2 < . . . < x n = b
(41)
∆x i = x i − x i −1 , M = max{∆x i | i = 1, 2, . . . , n}
(42)
olsun. Her bölüntü içinde bir x i −1 ≤ t i ≤ x i olacak şekilde bir t i noktası
seçelim. Şimdi tabanı ∆x i ve yüksekliğ h i = | f (t i )| olan dikörtgenin D
doğrusu etrafında bir tam dönüş yaptığını varsayalım. Yarıçapı h i olan
bir silindir oluşur. Bu silindirin hacmi
πh i2 ∆x i = π f (t i )2 ∆x i
(43)
HACIM HESAPL ARI
olacaktır. Bunların toplamı da asıl S cisminin hacmine yakın olacaktır.
V≈
n
X
π f (t i )2 ∆x i
(44)
i =1
Eğer M = max{∆x i } → 0 iken (44) toplamının limiti varsa, bu limit
V =π
b
Z
a
2
f (x) d x = π
b
Z
y2 d x
(45)
a
integrali ile ifade edilir ve bu intgral S cisminin hacmine eşit olur.
Dönme ekseni değişirse, Ox− ile O y− eksenlerini yer değiştirebiliriz:
V =π
d
Z
c
2
g (y) d y = π
d
Z
x2 d y
(46)
c
Şimdi dönen R düzlemsel bölgesinin üstten y = f (x), alttan y = g (x)
fonksiyonları ile sınırlı olduğunu düşünelim. Bu düzlem parçasının bir
tam dönüş yapmasıyla oluşan dönel katı cismin hacmı f ile g fonksiyonlarına karşılık gelen iki dönel katı cismin hacimleri farkıdır. Dolayısıyla;
V = V f − Vg = π
Z
b¡
a
¢
f 2 (x) − g 2 (x) d x
(47)
Silindirik Kabuklar Yöntemi
y = f (x), x = a, x = bveOx− ekseni ile çevrili düzlemsel bölgenin O y−
ekseni çevreinde bir tam dönüş yaptığını düşünelim. Bu dönme sonunda
x ve x + ∆x aralığı üzerindeki dar şeridin O y− ekneni çevresinde kabuğu
∆x kalınlığıda olan silindirik bir cisim oluşur. Bu silindirin merkex ekseni
O y− ekseni ve iç yarıça x dış yarıçapı, Şimdi η i ∈ [x, x + δ] olan bir η i
noktası düşünelim. η i noktasının sözkonusu dönüş esnasında çizdiği
çemberin uzunluğu 2πη i olacaktır. O halde η i üzerine kurulan silindirin
yüzey alanı
A(η i ) = 2πη i f (η i )
(48)
olacaktır. x i , ≤ η i ≤ x i + ∆x i olduğuna göre
f (x i )∆x i ≤ f (η i )∆x i ≤ f (x + ∆x i )∆x i
olmalıdır.
x + δx olur. [x, x + δx aralığının orta noktası
r=
x + x + ∆x
∆x
=x+
2
2
olur. Sözkonusu silindirin iç ve dış yüzeyleri maksimum ∆x → 0 iken,
söz konusu küçük aralığın r orta noktasından geçen silindir yüzeyine
yaklaşacaklardır. r orta noktası söyldiğimiz bir tam dönüş sonunda r
yarıçaplı bir çember çizer. Bu çemberin uzunluğu 2πr olduğuna göre,
silindir duvarının alanı
∆A = 2πr
35
36
CALCULUS
Dilimleme Yöntemiyle Hacim Bulma
Şekilde hacmi hesaplanacak bir cisim görülüyor. Uygun bir Ox- ekseni
seçelim. Eksenin hangi konumda seçildiği ancak pratik değer taşır.
Cismin her noktasından D doğrusuna dikmeler inildiğini varsayalım.
Dikmelerin ayaklarını içeren [a, b] aralığının bir bölüntüsünü (partition)
P ile gösterelim:
a = x 0 < x 1 < −x 2 < . . . < x n = b
(49)
∆x i = x i − x i −1 , M = max{∆x i | i = 1, 2, . . . , n}
(50)
olsun. x i noktasından D doğrusuna dikey olacak biçimde çizilen düzlem
S cismiyle kesişir ve onunla arakesiti düzlemsel bir R i bölgesi oluşturur.
R i bölgesinin alanına A(x i ) diyelim. Bölüntünün ardışık x −i −1 , x i noktalarından deçen dikey düzlemlerin S ile arakesitleri arasında kalan dilimi
düşünelim. Bu dilimin hacmı yaklaşık olarak, ∆x i = |x i − x i −1 | olmak üzere,
∆V (x i ) ≈ A(x i ).∆x i
(51)
olacaktır. Bu yaklaşık hacimlerin toplamı S cisminin V hacmine yakın
olur:
V≈
n
X
∆V (x i ) =
n
X
∆A(x i )∆x i
(52)
i =0
i =0
∆x i bölüntü aralıklarının M maksimum uzunluğu sifıra giderken (52)
toplamının limiti varsa söza konusu limit
Z b
V=
A(x) d x
(53)
a
integraline eşit olur. Bu değer S cismini hacmidir.
Kutupsal Koordinatlar
Kutupsal koordinatlara dönüşümü incelerken

x = r cos θ
T:
 y = r sin θ
Figure 36: Kutupsal koorinatlar
dönüşümü ile xOy- dikey kartezyen koordinat sisteminden (r , θ) kutupsal
koordinat sitemine nasıl dönüşüm yapıldığını incelemiştik. Bu kesimde,
bu dönüşümün katlı integrallerde kullanılışını ele alacağız.
Figure 37: Dönüşüm
r 2 = x 2 + y 2 , x = r cos θ, y = r sin θ
ve
¯
¯ ¯"
¯ ∂(x, y) ¯ ¯¯ ∂x
∂r
¯
¯
¯ ∂(u, v) ¯ = ¯¯ ∂x
∂θ
∂y
∂r
∂y
∂θ
#¯ ¯"
¯ ¯ cos θ
¯ ¯
¯=¯
¯ ¯ −r sin θ
#¯
¯
¯
¯=r
r cos θ ¯
sin θ
çıkar. Öyleyse aşağıdaki teoremi söyleyebiliriz:
Theorem 0.33. D = {(r , θ)| a ≤ r ≤ b, αθ ≤ β,
f fonksiyonu sürekli ise
Ï
Z
Z
f (x, y) d A = αβ
D
eşitliği sağlanır.
b
a
0 ≤ β − α ≤ 2π bölgesinde
f (r cos θ, r sin θ)r d r d θ
(54)
HACIM HESAPL ARI
37
Kanıt: Önceki kesimde ifade edilen Teorem 36’in varsayımları sağlandığından, sözkonusu teoremin burada geçerliolacağı açıktır.
Örnek 0.34. x 2 + y 2 ≤ 4 kapalı diski üzerindeki
Ï
D
(x 2 + y 2 + 1)d A
katlı integralini kutupsal koordinatlara dönüşüm yaparak hesaplayınız.
Çözüm:
Ï
D
(x 2 + y 2 + 1)d A =
2π Z 2
Z
0
0
¯2
r 2 ¯¯
+ ¯
4
2 0
2π µ r 4
Z
=
(r 2 + 1)r d r d θ
0
= 12π
Örnek 0.35. x 2 + y 2 = 4, x 2 + y 2 = e 2 çemberleri arasında kalan D halka
bölgesi üzerindeki
Ï
D
l n(x 2 + y 2 )d A
katlı integralini kutupsal koordinatlara dönüşüm yaparak hesaplayınız.
Çözüm:
Ï
D
2
2π Z e
Z
2
l n(r 2 )r d r d θ
µ
¶e
1
1
= 4π r 2 l nr − r 2
2
4
2
l n(x + y )d A =
0
0
= π(e 2 + 4 − 8l n2)
Theorem 0.36. R = {(r , θ)| α ≤ θ ≤ β,
r 1 (θ) ≤ r ≤ r 2 (θ), r 1 (θ) ≥ 0, r 2 (θ) ≥
0} bölgesinde f fonksiyonu sürekli ise
Ï
R
f (r , θ) d A =
Z
αβ
Z
r 2 (θ)
r 1 (θ)
f (r , θ)r d r d θ
(55)
eşitliği sağlanır.
Örnek 0.37. a yarıçaplı kürenin hacmini kutupsal koordinatları kullanarak hesplayınız.
Çözüm: x 2 + y 2 +z 2 = a 2 küresinin xy-düzleminin üstünde kalan yarısını
hacmini bulup çıkaı 2 ile çarpabiliriz.
Figure 38: Kürenin hacmi
z ≥ 0,
z=
q
r 2 − x2 − y 2
dir. Yarı kürenin x y düzlemi üzerindeki izdüşümü D = {(x, y)| x 2 + y 2 ≤
38
CALCULUS
a 2 dir. Buradan,
Z 2π Z r p
l n(r 2 − x 2 − y 2 ) d yd x = 2
a2 − r 2r d r d θ
D
0
0
¶a
Z 2π µ
3
1
− (a 2 − r 2 ) 2 d θ
=2
3
0
0
Z
´
3
3
2 2π ³ 2
=−
(a − a 2 ) 2 − (a 2 − 02 ) 2 d θ
3 0
Z
2 2π 3
=
(a θ d θ
3 0
¯2π
2
= (a 3 θ ¯0
3
4
= πa 3
3
Ï
V =2
Örnek 0.38. D bölgesi birinci dörtte birlik (first quadrant) bölgede
r = 3 cos θ diskinden ile r = 1 + cos θ kalp eğrisi (cardioid) atılınca
geri kalan bölge olsun.
Ï
D
1
dA
x
katlı integralini kutupsal koordinatlara dönüşüm yaparak hesaplayınız.
Çözüm: 3 cos θ = 1 + cos θ ⇒ 2 cos θ = 1, cos θ =
Figure 39: Alan
Ï
D
1
dA=
x
π/3 Z 3 cos θ
Z
0
1+cos θ
π/3 Z 3 cos θ
0
1+cos θ
Z
=
π/3
Z
=
0
π/3
Z
=
0
π/3
Z
=
0
1
2
⇒θ=
π
3
olduğundan,
1
rdrdθ
r cos θ
sec θ d r d θ
cos θ
r sec θ|31+cos
θ dθ
(3 cos θ sec θ − (1 + cos θ) sec θ) d θ
/2 − sec θ)d θ
= 2θ − l n| sec θ + tan θ||π/3
0
p
2π
=
− l n(2 + 3)
3
Örnek 0.39. D bölgesi birinci dörtte birlik (first quadrant) bölgesi olsun.
Bu sınırsız bölgede,
Ï
e −(x
2 +y 2 )
dA
D
katlı integralini kutupsal koordinatlara dönüşüm yaparak hesaplayınız.
Çözüm: Bu has olmayan bir integraldir. Öyleyse, Kutupsal koorinat
HACIM HESAPL ARI
sistemine geçerek,
Ï
e −(x
2 +y 2 )
π/2 Z n
Z
2
e −r r d r d θ
0
¯ ¶
Z π/2 µ
1 −r 2 ¯¯n
= lim
− e ¯ dθ
n→∞ 0
2
0
¶
Z π/2 µ
1 −n 2 1
= lim
− e
+ dθ
n→∞ 0
2
2
¯π/2
´
³
¯
2
1
= lim
1 − e −n .θ ¯¯
n→∞ 2
0
´
2
π³
= lim
1 − en
n→∞ 4
π
=
4
d A = lim
n→∞ 0
D
Örnek 0.40.
∞
Z
I=
e
−x 2
0
p
π
dx =
2
olduğunu gösteriniz.
Çözüm:
∞
Z
I=
Z0 a
Ia =
2
e −x d x
2
e −x d x
0
dersek, değişken adını serbestçe seçebildiğimizi de düşünerek,
(I a )2 =
a
µZ
2
e −x d x
Ï0
2
e −y d y
¶
0
e
=
a
¶ µZ
−(x 2 +y 2 )
d xd y
R
p
π
=
2
(önceki problemden)
çıkar. Önceki problemin sonucunun bilinmediğini, varsayarak çözümü
bulabiliriz. Şimdi, birinci dörtte birlik (first quadrant) bölgede R 1 bölgesi
p
a yarıçaplı disk, R bölgesi kenar uzunluğu a olan kare, R 2 bölgesi 2a
yarıçaplı disk olmak üzere,
Ï
e
−(x 2 +y 2 )
R1
Ï
d xd y ≤
e
−(x 2 +y 2 )
R
Ï
d xd y ≤
e −(x
2 +y 2 )
d xd y
R2
yazabiliriz. Kutupsal koordinatları kullanırsak,
π/2 Z a
Z
e
0
buradan,
0
−r 2
2
r d r d θ ≤ (I a ) ≤
p
2a
π/2 Z
Z
0
0
´
´
2
2
π³
π³
1 − e −r ≤ (I a )2 ≤
1 − e −2a
4
4
lima→∞ için istene sonuç elde edilr:
∞
Z
I=
0
2
e −x d x =
p
π
2
2
e −r r d r d θ
39
40
CALCULUS
Alıştırmalar
1. D = {(x, y)| π2 ≤ x 2 + y 2 ≤ 4π2 } ise
¶
µq
Ï
x 2 4y 2 d xd y
cos
D
integralini hesaplayınız.
2. z = x 2 + y 2 parabolünün altında, x y− düzleminin üstünde ve x 2 + y 2 =
2x silindirinin içinde kalan katı cismin havcini bulunuz.
p
3. x 2 + y 2 + z 2 = 1 küresi ile üstten ve z = x 2 + y 2 konisi ile alttan sınırlı
bölgenin hacmini bulunuz.
p
4. D bölgesi x = 4 − y 2 yarıçemberi ve y−ekseni ile sınırlı bölge ise,
Ï
2
2
e −x −y d A
D
integralini hesaplayınız.
5. D bölgesi x 2 + y 2 = 4,
x 2 + y 2 = 4, çemberleri ile sınırlı bölge ise,
Ï
x dA
D
integralini hesaplayınız.
6. D bölgesi x 2 + y 2 = 4,
x 2 + y 2 = 4, çemberleri sınırlı bölge ise,
p
Z 1Z
a 2 −x 2
ex
2 +y 2
d xd y
0
0
integralini hesaplayınız.
7.
Z
a
Z pa 2 −y 2
−a 0
3
(x 2 + y 2 ) 2 d xd y
integralini hesaplayınız.
8.
Z 4 Z p16−y 2
p
0
16−y 2
−
(x 2 .y 2 ) d xd y
integralini hesaplayınız.
9.
p
2x−x 2 q
Z 2Z
0
0
x 2 + y 2 d yd x
integralini hesaplayınız.
10. Aşağıdaki ntegralleri tek bir integral işareti atında yazınız.
Z
1
Z
x
p p
1/ 2
1−x 2
p Z
2 x
Z
x y d yd x +
integralini hesaplayınız.
1
0
Z
x y d yd x +
2
Z
p
2 0
p
4−x 2
x yd yd x
Fiziksel uygulamalar
Düzlemsel bölgelerin kütle merkzi
Tanım 0.41. Düzlemsel bi bölgenin kütle merkezi, bütün noktalarının
konsantre olduğu kabul edilen (x, y noktasıdır.
Düzlemsel bir A bölgesinin (x, y kütle merkezi
Z
M y = x A = xd A
Z
M x = y A = yd A
(56)
(57)
(58)
eşitliklerini sağlar. Bu eşitliklerden
R
xA =
yA =
xd A
R A
yd A
A
(59)
(60)
bağıntıları çıkarılır.
Ağırlık Merkezi Bulma Problemleri
Mekanikte bir cismin kütle merkezi (ağırlık merkezi), cismin bütün
noktalarının konsantre olduğu bir noktadır.
1. x32 + y 2 = 25 çemberinin sınırladığı diskin ikinci dörttebirlik böldede
(second quadrant) kalan kısmının ağırlık merkezini bulunuz.
Çözüm:
A=
π 2 25
5 =
π
4
4
Z 0 p
4
20
x 25 − x 2 d x = −
25π −5
3π
Z 0 q
4
20
y=
y 25 − y 2 d x = −
25π −5
3π
x=
(61)
(62)
(63)
(64)
olur.
42
CALCULUS
2. x 2 + y 2 = a 2 ile sınırlı birim diskin birinci dörtte birlik bölgede (first
quadrant) kalan kısmının kütle merkezini bulunuz.
Çözüm:
Yoğunluğun her yerde aynı ve olduğunu varsayalım δ = 1 olur.
d m = δd A
q
= a2 − y 2 d y
Z
a
Mx =
y dm
Z0 a q
=
y a2 − y 2 d y
0
Z
q
−1 a
(−2y) a 2 − y 2 d y
=
2 0
µq
¶ 3 ¯¯a
2¯
−2
2
2
=
a −y
¯
¯
3(2)
0
1
= a3
3
y=
Mx
A
=
a3
3
πa 2
4
=
4a
3π
x=
My
simetri nedeniyle
A
4a
=
3π
3. y = h 2 − x 2 parabolü ile Ox−ekseni arasında kalan bölgenin kütle
merkzini bulunuz.
Çözüm:
Z Z
Mx =
dA
Z
=
=
=
R
+h Z h 2 −x 2
ydy
−h 0
Z +h
1
−h
2
8 5
h
15
(h 2 − x 2 )2 d x
FIZIKSEL UYGULAMALAR
Z Z
A=
dA
R
+h Z h 2 −x 2
Z
=
y d yd x
−h 0
Z +h
=
(h 2 − x 2 ) d x
−h
¯
1 3 ¯¯h
= h x− x ¯
3
−h
4 3
= h
3
2
Mx
A
2h 2
=
5
y=
Z Z
My =
xd A
R
+h Z h 2 −x 2
Z
x d yd x
=
Z
=
−h 0
+h
−h
x(h 2 − x 2 ) d x
==
x=
My
A
0
=
A
=0
4. Birim kareden birim disk çıkarılıyor. Geri kalan üçgen benzeri düzlemsel bölgenin ağırlık merkezini bulunuz.
Çözüm:
Birim kareyi koordinat eksenind x = 1, y = 1 doğruları ile koordinat
eksenlerinin sınırladığı düzlemsel bölgedir. Birim disk x 2 + y 2 = 1
çemberi ve içidir. Şekilden birim kareden birim disk atılınca kalan
bölge görülüyor.
Problemi daha genel tutmak içim 1 yerine a alalım.
Z Z
Mx =
yd A
Z a RZ a
=
y d yd x
p
0
a 2 −x 2
Z a
¡ 2
¢
1
=
a − (a 2 − x 2 ) d x
2 0
Z
1 a 2
=
x dx
2 0
1
= a3
6
43
44
CALCULUS
aZ a
Z
A=
p
0
a 2 −x 2
d yd x
π 2
a
4
a 2 (4 − π)
=
4
= a2 −
Mx
A
4
a3
=
2
6 a (4 − π)
2a
=
12 − 3π
y=
Simetri nedeniyle,
x=
2a
12 − 3π
olur.
5. y = si nx, 0 ≤ x ≤ π ile Ox− ekseni arasında kalan düzlemsel bölgenin
ağırlık merkezini bulunuz.
Çözüm:
Z Z
Mx =
yd x
R
πZ
Z
si nx
(yd y)d x
=
0
0
π
1
si n 2 x d x
2 0
Z
1 π
=
(1 − cos2x) d x
4 0
1
1
= π − si n2π
4
8
1
= π
4
Z
=
Z Z
yd A
A=
R
π Z si nx
Z
=|
d y d x|
Z0 π
=|
0
si nx d x|
0
= |cosx|π0 |
= | − 1 − 1|
=2
Mx
A
1
= π
8
My
x=
A
1
= π
2
y=
simetri nedeniyle
FIZIKSEL UYGULAMALAR
Alıştırmalar
Aşağıda verilen eğrilerle sınırlanmış düzlemsel bölgelerin kütle merkezlerini bulunuz.
( 95 , 95 )
1. y 2 = 4x, x 2 = 4y;
1 e+1
( e−1
, 4 )
2. y = e x , x = 0, x = 1, y = 0;
(πa, 5a
6 )
3. x = a(θ − si nθ), y = a(1 − cosθ);
4. x = asi nθ, y = acosθ;
4a
( 4a
3i , 3i )
Yay’ın Kütle merkezi
Düzlemsel bölgenin kütle merkezine benzer olarak bir yay’ın kütle
merkezi tanımlanabilir:
Z
M y = sx =
xd s
Z
Mx = s y =
yd s
Örnek:
p
y = a 2 − x 2 , a > x, x > 0 yayının kütle merkezini bulunuz.
Çözüm:
Z
Mx = y s = y
a
Z
ds = ya
y=
0
p
¯
x ¯a y aπ
y asi n −1 ¯¯ =
a 0
2
a2 − x2
dx
2a
π
x =0
simetri
Alıştırmalar
Aşağıdaki yayların kütle merkezlerini bulunuz:
1. x = 3t 2 , y = 6t , 0 ≤ t ≤ 2
2. x = e −t cost , y = e −t si nt , 0 ≤ t ≤ 2π
3. x = e y , 0 ≤ y ≤ 1
4. x = asi n 3 t , y = acos 3 t
5. y = coshx, −1 ≤ x ≤ 1
Yoğunluk
Bir cismin P noktasını içeren küçük bir elementini ∆V ile ve ∆V nin
kütlsini ∆m ile gösterlim. Eğer
∆m
∆V t o0 δV
δ = lim
(65)
45
46
CALCULUS
limiti varsa, buna cismin P noktasındaki yoğunluğu denilir. Bu tanımdan
anlaşıldığı gibi, bir cismin yoğunluğu sabit olmayabilip her noktada farklı
bir yoğunluğa sahip olabilir. Tabii, bazı cisimlerde yoğunluk her noktada
aynı olabilir. (134) limitini
δ=
dm
dV
dersek,
d m = δdV
(66)
biçiminde de yazabiliriz. Şimdi bir cismin kütlesi ∆m olan çok küçük
∆V parçacıklarına ayrıldığını varsayalım. Her parçacığın içerdiği P
noktasındaki yoğunluğun δ olduğunu kabul edersek,
∆m ≈ δ∆V
(67)
yazabiliriz. Şimdi bütün cismin bir noktaya yoğunlaştını ve bu noktanın
koordinantlarının
x̃∆m,
ỹ∆m,
z̃∆m
(68)
koşulunu sağladığını varsayalım. ∆V → 0 iken, () ifadelerinden, koordinat
düzlemlerine göre cismin momentlerini yazabiliriz:
Z
Myz =
Z
x̃d m,
M zx =
Z
ỹd m,
Mx y =
z̃d m
(69)
Buradan , kütle merkezinin koordinatlarını yazabiliriz:
R
x= R
x̃d m
dm
R
y= R
,
ỹd m
dm
R
,
z= R
z̃d m
dm
(70)
Moment
Noktaya Göre Moment
Tanım 0.42. Bir parçacığın sabit bir noktaya göre momenti, parçacığın
Figure 40: Moment
noktaya olan uzaklığı ile kütlesinin çarpımına eşittir.
Parçacığın kütlesi m ve sabit noktaya olan uzaklığı d ise moment d m
dir.
Doğru üzerinde Moment
Figure 41: Moment
Bir doğru üzerinde konuşlanan ve kütleleri m 1 , m 2 , . . . , m n olan n-tane
parcağın her birisinin doğru üzerideki sabit bir O noktasına uaklıkları,
sırasıyla, x 1 , x 2 , . . . , x n ise, bu parçacıklardan oluşan cismin O noktasına
göre momenti,
n
X
xk mk
(71)
k=1
sayısıdır. Bütün kütlenin söz konusu doğru üzerindeki x noktasına
yığıldığını varsayarsak
kütlesinin momenti
Ã
x
X
mk = M
n
X
!
k=1
m k = xM
(72)
FIZIKSEL UYGULAMALAR
47
olur. Yukarıdaki varsayımlar altında, kütlenin sabit noktaya olan uzaklığı
olarak alınan x sayısına M cisminin kütle merkezi denilir. Buradan şunu
yazabiliriz:
Pn
x=
x m
k=1 k k
Pn
m
k=1 k
Pn
x m
k=1 k k
=
M
(73)
Buna göre,bir cisim n-tane parçacıktan oluşuyor ve n-tane parçacığın
her birisinin kütlesi m 1 , m 2 , . . . , m n ve O y− eksenine uzaklıkları x 1 , x 2 , . . . , x n
ise cismin O y− eksenine göre momenti
My =
n
X
mi xi
(74)
i =1
olur. Aynı cisim için Oy-ekseni yerine Ox− eksenini koyarak, cismin Ox−
eksenine göre momentinin
Mx =
n
X
mi y i
(75)
i =1
olduğunu söyleyebiliriz.
Kütle Merkezi
Tanım 0.43.
Kütlesi M =
n
X
mi
(76)
i =1
olan bir cisim düşünelim. Sabit bir koordinat sistemine göre,
M x = My
M y = Mx
ve
(77)
koşulunu sağlayan (x, y) noktasına cismin kütle merkezi denilir.
Noktanın Eksene Göre Momenti
Şimdi parçacıkların bir doğru üzerinde değil de bir düzlem içine serpilmiş olduklarını düşünelim. Düzlemde sabit bir doğruya göre bu
parçacıkların momentlerini bulmak istiyoruz. Önce bir parçacığın sabit
doğruya göre momentini tanımlayalım:
Tanım 0.44. Kütlesi m olan bir parçacığın sabit bir doğruya uzaklığı d ise,
parçacığın doğruya göre momenti d m dir.
Fiziksel uygulamalarda parçacığın koordinat eksenlerine göre momenti söz konusu olur. Buna göre, düzlem üzerinde koordinatları
(x 1 , y 1 ), (x 2 , y 2 ), . . . , (x n , y n )
olan n-tane patçacığın her birisinin kütlesi, sırasıyla,
m1 , m2 , . . . , mn
ise, bu parçacıkaların koordinat eksenlerine göre momentleri;
My =
Mx =
n
X
i =1
n
X
i =1
xk mk
(78)
y k mk
(79)
Figure 42: Moment
48
CALCULUS
olur. Bu parçacıklardan oluşam M cisminin bir (x, y) noktasınna yoğunlaştığını varsayarsak, bu noktaya söz konusu koordinat sistemine göre
cismin kütle merkezi denilir. Söylediklerimizden şu bağıntıları yazabilirz:
Pn
i =1 x k m k
Pn
i =1 m k
x=
Pn
i =1
y= P
n
y k mk
i =1 m k
Pn
=
i =1 x k m k
M
(80)
Pn
=
i =1 y k m k
M
(81)
Düzleme Göre Moment
Kütlesi m olan bir parçacığın uzayda sabit bir düzleme uzaklığı d ise,
parçacığın sabit düzleme göre momenti d m dir.
(x 1 , y 1 , z 1 ), (x 2 , y 2 , z 2 ), . . . , (x n , y n , z n )
Figure 43: Moment
noktalarının üç boyutlu uzayda serpiştirildiğini düşünelim. Bu noktaların
sabit bir koordinat sisteminde koordinat düzlemlerine göre momenti,
sırasıyla,
Myz =
M zx =
Figure 44: Moment
Mx y =
n
X
k=1
n
X
k=1
n
X
xk mk
(82)
y k mk
(83)
xk mk
(84)
k=1
(85)
olur. Burada, örneğn y z düzlemi yOz koordinat düzlemidir. Bu düzlemlere göre kütle merkezinin koordinatları
Pn
Pn
xk mk
x m
k=1 k k
= k=1
x = Pn
m
M
k
Pn
Pn k=1
y
m
y k mk
k
k
k=1
y = Pn
= k=1
mk
M
Pnk=1
Pn
z m
zk mk
k=1 k k
z= P
= k=1
n
m
M
k=1 k
(86)
(87)
(88)
(89)
olur.
Fiziksel dünyada kütle parçacıklarına ayrılmamış sürekli bir bütündür.
O tür cisimlerin kütle merkezleri ve momentleri için limit işleminden
Figure 45: Moment
yararlanırız. Anımsarsanız, integrali sonlu toplamların limiti olarak
tanımlamıştır. Fiziksel uygulamlarda da hep aynı işi yapacağız.
Alanı A olan düzlemsel bir R bölgesinin kordinat eksenlerne göre
momentleri, sırasıyla,
Ï
mx =
Ï
yd A,
R
My =
xd A
(90)
R
biçiminde tanımlanır. Düzlemsel R bölgesinin, aynı düzlemdeki sabit bir
koordinat sistemine göre (x, y) ile gösterilen kütle merkezi,
x A = My
y A = Mx
FIZIKSEL UYGULAMALAR
eşitliğini sağlayan
Î
x = ÎR
xd A
RdA
Î
yd A
y = ÎR
,
(91)
RdA
Bir Düzlem Parçasının Bir Eksene Göre Momenti
A bir düzlemsel alan ve d bir doğru olsun. Şekil ??’de görüldüğü gibi, A
bölgesini ∆A i dar şertlerine bölelim. Şerit içinde alınan bir noktanı d
doğrusuna uzaklığı l i olsun.
n
X
l i δA i
(92)
i =1
toplamının , max|A i | → 0 iken (92) limitine A alanının d doğrusuna göre
momenti denilir. Bu ifadeden;
Md =
n
X
lim
max|A i |→0 i =1
l i δA i =
Z
ldA
(93)
çıkar. Tabii, sağdaki integrain bürün A alanı üzrinden alındığı açıktır.
Tek değişkenli fonksiyonla çalışıyorsak, M d hesaplanırken alanı
çevreleyen y = f (x), y = g (x) fonksiyonlarının olduğunu ve d A nın d x
cinsinden ifadwe edildiğini varsay yoruz.
Örnek
y = 13 x 2 parabolü ilşe y = x doğrusu arasınada kalan alanın O y−
eksenine gör momemntini bulunuz.
Çözüm:
Z
My =
3
xdA
0
3
1
x(x x 2 ) d x
3
0
x3 x34
=
−
3
12
Z
=
= 2.25
Bir Yayın Momenti
Düzlemsel alanların momemtlerini bulurken izlediğimiz yönteme benzer
yöntemle bir yayın bir doğruya göre momentini bulabiliriz:
Z
Md = l d s
(94)
burada l yaya ait noktanın doğruya uzaklığıdır.
Örnek
Üst yarı düzlemdeki çember yayının Ox− eksenine göre momentini
bulunuz.
Çözüm:
Üst yarı düzlemdeki çember yayının denklemi y =
p
a2 − x2,
(y ≥ 0)
dir. Yay uzuluğu
ds =
q
1 + y 02 d x = p
a dx
a2 − x2
(95)
49
50
CALCULUS
dir. Buradan,
Z
Mx =
y ds
+a
Z
=
−a
p
a a2 − x2
dx
p
a2 − x2
= ax|+a
−a
= a2 − a2 = 0
Örnek
I.dörtte birlik bölgedeki (first quadrant) çember yayının Ox− eksenine
göre momentini bulunuz.
Çözüm:
I.dörtte birlik bölgedeki çember yayının denklemi y =
p
a2 − x2,
(0 ≤
x ≤ a dir. Yay uzuluğu
ds =
q
1 + y 02 d x = p
a dx
(96)
a2 − x2
dir. Buradan,
Z
Mx =
y ds
+a
Z
=
0
p
a a2 − x2
dx
p
a2 − x2
= ax|+a
0
= a2 − 0 = 0
Uygulamalar
Aşağıdaki yayların koordinat eksenlerine göre momentlerini bulunuz.
1. y 2 = 8x,
2. y = e x ,
0≤x ≤4
0≤x ≤1
3. y = cos x,
4. y = cosh x,
0≤x ≤
π
2
−1 ≤ x ≤ 4
5. y = a(θ − sin θ), y = a(1 − cos θ),
6. y = a cos θ, y = b sin θ,
c ycl oi d
0≤θ≤π
Örnek
Üst yarı düzlemdeki yarı diskin y = −r eksenine göre momentini
bulunuz.
Çözüm:
Üst yarı düzlemdeki yarı yarı diskin üst sınırı y =
p
a2 − x2,
(−a ≤ x ≤
FIZIKSEL UYGULAMALAR
a), ve alt sınırı y = 0 doğrusudur. Buna göre;
Ï
M y+r =
xdA
R
Z
+r
Z
−r
+r
p
r 2 −x 2
Z
x d xd y
=
−r
(
=
p
−r
r 2 − x 2 + r )x d x
´+r
3
1³ 2
(r − x 2 ) 2 + r x
−r
2
=−
= −r 2
Örnek
x = a, y = a karesinden a yarıçaplı çember çıkarılıyor. Geri kalan
düzlemsel bölgenin ağırlık merkezini bulunuz.
Çözüm:
Z Z
Mx =
ydA
R
aZ a
Z
=
p
0
a 2 −x 2
y d yd x
¢
1 a¡ 2
a − (a 2 − x 2 ) d x
2 0
Z
1 a 2
=
x dx
2 0
1
= a3
6
Z
=
aZ a
Z
A=
p
0
a 2 −x 2
2
d yd x
πa
4
a 2 (4 − π)
=
4
= a2 −
Simetri nedeniyle;
x=
2a
12 − 3π
yazılabilir.
Üç Katlı İntegral İle Moment
4
4
(x, y, z) noktasındaki yoğunluğu ρ(x, y, z) ile österelim. T katı cisminin
kütlesi,
Ñ
m=
T
ρ(x, y, z)dV
dir. Koordinat düzlemlerine göre momentler,
Ñ
Mx y =
zρ(x, y, z)dV
ÑT
M xz =
yρ(x, y, z)dV
ÑT
Myz =
xρ(x, y, z)dV
T
(97)
(98)
(99)
(100)
Yoğunluk, birim hacim başına düşen
kütledir.
51
52
CALCULUS
eşitlikleri ile tanımlanır.
56
T cisminin kütle merkezi (x, y, z)’nin koordinatları,
x=
Myz
m
,
y=
M xz
,
m
z=
Mx y
m
(101)
dir.
7
eylemsizlik momenti
7
T cisminin eylemsizlik momentleri,
Ñ
Ix =
(y 2 + z 2 )ρ(x, y, z)dV
T
Ñ
Iy =
(x 2 + z 2 )ρ(x, y, z)dV
T
Ñ
Iz =
(x 2 + y 2 )ρ(x, y, z)dV
(102)
(103)
(104)
T
dir.
Örnek 0.45. Birinci sekizde birlik (octant) bölgede yer alan x + y + z = 1
16
düzgün dörtyüzlüsünün yoğunluk fonksiyonu ρ(x, y, z)) (1+x+y+z)
3 ) dür.
Kütlesini bulunuz.
Çözüm:
Figure 46: Düzgün Dörtyüzlü
Dörtyüzlüyü T ile gösterelim:
Ñ
15
m=
ρ(x, y, z)
dV
(1 + x + y + z)3
T
Z 1 Z 1−x Z 1−x−y
d zd yd x
= 16
(1 + x + y + z)3 )
0 0
0
¯1−x−y
Z 1 Z 1−x µ
¯
1
1
¯
d yd x
= 16
2
2 (1 + x + y + z) ) ¯0
0 0
¶
Z 1 Z 1−x µ
1
1
=8
−
dy
(1 + x + y + z)2 ) 4
0 0
¯
Z 1µ
1
y ¯1−x
=8
−
− ¯¯
dx
1+x + y 4 0
0
¶
Z 1µ
1
x −3
+
dx
=8
x +1
4
0
µ
¶¯
1
3 ¯1
= 8 l n(x + 1) + x 2 − x ¯¯
8
4
0
= 8 ln 2 − 5
olur.
Work (İş)
İş günlük yaşamda farklı anlamlara sahiptir. Biz burada yalnızca işin
fiziksel anlamı üzerinde duracağız. İşin fiziksel anlamı, bir kuvvetin
etkisiyle cismin yer değiştirmesiyle orantılı oluşan fiziksel niceliktir. Buna
göre, örneğin, üstündeki büyük ağırlığı taşıyan bir köprünün ayakları hiç
iş yapmıyor. Ağır bavulunu elinde tutan ama hareketsiz duran kişinin
kol kasları ağrısa bile hiç iş yapmıyor. Ama o bavulu alıp bineceği taşıtın
rafına koyarsa bir iş yapmış olur.
FIZIKSEL UYGULAMALAR
Tanım 0.46. Sabit bir kuvvet x-ekseni boyunca bir cisme etki ediyor ve
cisim a noktaından b noktasına gidiyorsa, yapılan iş
W = F (b − a)
(105)
olarak tanımlanır.
Başka bir deyişle, iş, kuvvet ile cismin aldığı yolun çarpımıdır.
Tanım 0.47. Bir F kuvvetinin etkisiyle hareket eden cisim F vektörünün
doğrultusunda s kadar yol giderse, yapılan iş
W =Fs
(106)
dir.
Fiziksel olayların çoğunda olduğu gibi, F kuvveti sabit olmayabilir; noktadan noktaya değişebilir. Bu durumda cismin s kadar yer
değiştirmesini küçük ∆s aralıklarının toplamı olarak düşünürüz. Böylece
yapılan işi bir integralle ifade etme olanağı doğar.
Bunu biraz ayrıntılı açıklayalım: Bir cisim sürekli bir kuvvetin etkisiyle
a noktasından b noktasına gitsin. F kuvveti sabit olmasın ve her x noktasındaki değeri f (x)e eşit olsun. F (x) fonksiyonunu sürekli varsayalım.
[a, b] aralığını a = x 1 < x 2 < . . . < x n = b ve ∆x i = x i − x i −1 koşulunu
sağlayan küçük [x i −1 , x i ] aralıklarına bölelim. Başka bir deyişle [a, b]
aralığının bir ayrışımını (partition) oluşturalım. t i ∈ [x i −1 , x i ] olmak üzere
kuvvetin t i noktasında f (t i ) olduğunu varsayalım. Cismin a noktasından
b noktasına gitmesi halinde yapılan iş yaklaşık olarak
W≈
n
X
f (t i )∆x i
(107)
i =1
olcaktır. Şimdi max 1≤i ≤n |∆x i | −→ 0 iken
W=
lim
n
X
max∆x i →0 i =1
Z
f (t i )∆x i =
b
f (x) d x
(108)
a
olur.
Örnek:
Helikoid biçimindeki bir yayın doğal uzunluğu 10 cm’dir. yayın 2 cm
gerilmesi (genişlemesi) için 3 gr kuvvet gerekiyor. yayın doğal halinden
15cm gerilmesi halinde yapılan iş ne kadardır?
Çözüm:
Hook kuralına göre, yayın doğal halinden x kadar sündürülmedi için
gereken F (x) kuvvetinin
F (x) = kx
(k yaya bağlı sabit)
(109)
olduğu bilinir. Asıl problemi çözmek için k sabitini bulmalıyız. Verienlerden;
F (2) = 3 ⇒ 3 = 2km ⇒ k =
3
3
⇒ F (x) = x
2
2
çıkar. Bu değeri (108)’de kullanırsak,
5
Z
W=
0
¯5
3
3 x 2 ¯¯
3
3
x d x = x ¯ = (25 − 0) = 18
2
2 2 0 4
2
53
54
CALCULUS
olur.
Örnek:
2
kütleleri m 1 ve m 2 oln cisimlerinin birbirlerini çekimleri G m1s.m
2
bağıntısı ile verilir. Bu bağıntıda G sayısı çekim (gravitasyon) katsayısı
denilen bir sabit, s ise iki cisim arasındaki uzaklıktır. Kütlesi m 1 oln
cisme göre kütlesi m 2 olan cismin s 1 konumundans 2 konumuna gitmesi
halinde yapılan iş nedir?
Çözüm:
Z
W=
s2
s1
Z
F (x) d x =
s2
s1
Ã
!
m 1 .m 2
1
1
G
d x = g m − 1m 2 2 − 1 )
s2
s2 s1
Düzlemsel Bölgelerin Kütle Merkezi
Tanım 0.48. Düzlemsel bi bölgenin kütle merkezi, bütün noktalarının
konsantre olduğu kabul edilen (x, y noktasıdır.
Düzlemsel bir A bölgesinin (x, y kütle merkezi
Z
M y = x A = xd A
Z
M x = y A = yd A
(110)
(111)
(112)
eşitliklerini sağlar. Bu eşitliklerden
R
xA =
yA =
xd A
R A
yd A
A
(113)
(114)
bağıntıları çıkarılır.
Ağırlık Merkezi Bulma Problemleri
Mekanikte bir cismin kütle merkezi (ağırlık merkezi), cismin bütün
noktalarının konsantre olduğu bir noktadır.
1. x32 + y 2 = 25 çemberinin sınırladığı diskin ikinci dörttebirlik böldede
(second quadrant) kalan kısmının ağırlık merkezini bulunuz.
Çözüm:
A=
π 2 25
5 =
π
4
4
Z 0 p
4
20
x=
x 25 − x 2 d x = −
25π −5
3π
Z 0 q
4
20
y=
y 25 − y 2 d x = −
25π −5
3π
(115)
(116)
(117)
(118)
olur.
FIZIKSEL UYGULAMALAR
2. x 2 + y 2 = a 2 ile sınırlı birim diskin birinci dörtte birlik bölgede (first
quadrant) kalan kısmının kütle merkezini bulunuz.
Çözüm:
Yoğunluğun her yerde aynı ve olduğunu varsayalım δ = 1 olur.
d m = δd A
q
= a2 − y 2 d y
Z
a
Mx =
y dm
Z0 a q
=
y a2 − y 2 d y
0
Z
q
−1 a
(−2y) a 2 − y 2 d y
=
2 0
µq
¶ 3 ¯¯a
2¯
−2
2
2
=
a −y
¯
¯
3(2)
0
1
= a3
3
y=
Mx
A
=
a3
3
πa 2
4
=
4a
3π
x=
My
simetri nedeniyle
A
4a
=
3π
3. y = h 2 − x 2 parabolü ile Ox−ekseni arasında kalan bölgenin kütle
merkzini bulunuz.
Çözüm:
Z Z
Mx =
dA
Z
=
=
=
R
+h Z h 2 −x 2
ydy
−h 0
Z +h
1
−h
2
8 5
h
15
(h 2 − x 2 )2 d x
55
56
CALCULUS
Z Z
A=
dA
R
+h Z h 2 −x 2
Z
=
y d yd x
−h 0
Z +h
=
(h 2 − x 2 ) d x
−h
¯
1 3 ¯¯h
= h x− x ¯
3
−h
4 3
= h
3
2
Mx
A
2h 2
=
5
y=
Z Z
My =
xd A
R
+h Z h 2 −x 2
Z
x d yd x
=
Z
=
−h 0
+h
−h
x(h 2 − x 2 ) d x
==
x=
My
A
0
=
A
=0
4. Birim kareden birim disk çıkarılıyor. Geri kalan üçgen benzeri düzlemsel bölgenin ağırlık merkezini bulunuz.
Çözüm:
Birim kareyi koordinat eksenind x = 1, y = 1 doğruları ile koordinat
eksenlerinin sınırladığı düzlemsel bölgedir. Birim disk x 2 + y 2 = 1
çemberi ve içidir. Şekilden birim kareden birim disk atılınca kalan
bölge görülüyor.
Problemi daha genel tutmak içim 1 yerine a alalım.
Z Z
Mx =
yd A
Z a RZ a
=
y d yd x
p
0
a 2 −x 2
Z a
¡ 2
¢
1
=
a − (a 2 − x 2 ) d x
2 0
Z
1 a 2
=
x dx
2 0
1
= a3
6
FIZIKSEL UYGULAMALAR
aZ a
Z
A=
p
0
a 2 −x 2
d yd x
π 2
a
4
a 2 (4 − π)
=
4
= a2 −
Mx
A
4
a3
=
2
6 a (4 − π)
2a
=
12 − 3π
y=
Simetri nedeniyle,
x=
2a
12 − 3π
olur.
5. y = si nx, 0 ≤ x ≤ π ile Ox− ekseni arasında kalan düzlemsel bölgenin
ağırlık merkezini bulunuz.
Çözüm:
Z Z
Mx =
yd x
R
πZ
Z
si nx
(yd y)d x
=
0
0
π
1
si n 2 x d x
2 0
Z
1 π
=
(1 − cos2x) d x
4 0
1
1
= π − si n2π
4
8
1
= π
4
Z
=
Z Z
yd A
A=
R
π Z si nx
Z
=|
d y d x|
Z0 π
=|
0
si nx d x|
0
= |cosx|π0 |
= | − 1 − 1|
=2
Mx
A
1
= π
8
My
x=
A
1
= π
2
y=
simetri nedeniyle
57
58
CALCULUS
Alıştırmalar
Aşağıda verilen eğrilerle sınırlanmış düzlemsel bölgelerin kütle merkezlerini bulunuz.
( 95 , 95 )
1. y 2 = 4x, x 2 = 4y;
1 e+1
( e−1
, 4 )
2. y = e x , x = 0, x = 1, y = 0;
(πa, 5a
6 )
3. x = a(θ − si nθ), y = a(1 − cosθ);
4. x = asi nθ, y = acosθ;
4a
( 4a
3i , 3i )
Yay’ın Kütle merkezi
Düzlemsel bölgenin kütle merkezine benzer olarak bir yay’ın kütle
merkezi tanımlanabilir:
Z
M y = sx =
xd s
Z
Mx = s y =
yd s
Örnek:
p
y = a 2 − x 2 , a > x, x > 0 yayının kütle merkezini bulunuz.
Çözüm:
Z
Mx = y s = y
a
Z
ds = ya
y=
0
p
¯
x ¯a y aπ
y asi n −1 ¯¯ =
a 0
2
a2 − x2
dx
2a
π
x =0
simetri
Alıştırmalar
Aşağıdaki yayların kütle merkezlerini bulunuz:
1. x = 3t 2 , y = 6t , 0 ≤ t ≤ 2
2. x = e −t cost , y = e −t si nt , 0 ≤ t ≤ 2π
3. x = e y , 0 ≤ y ≤ 1
4. x = asi n 3 t , y = acos 3 t
5. y = coshx, −1 ≤ x ≤ 1
Yoğunluk
Bir cismin P noktasını içeren küçük bir elementini ∆V ile ve ∆V nin
kütlsini ∆m ile gösterlim. Eğer
∆m
∆V t o0 δV
δ = lim
(119)
FIZIKSEL UYGULAMALAR
limiti varsa, buna cismin P noktasındaki yoğunluğu denilir. Bu tanımdan
anlaşıldığı gibi, bir cismin yoğunluğu sabit olmayabilip her noktada farklı
bir yoğunluğa sahip olabilir. Tabii, bazı cisimlerde yoğunluk her noktada
aynı olabilir. (134) limitini
δ=
dm
dV
dersek,
d m = δdV
(120)
biçiminde de yazabiliriz. Şimdi bir cismin kütlesi ∆m olan çok küçük
∆V parçacıklarına ayrıldığını varsayalım. Her parçacığın içerdiği P
noktasındaki yoğunluğun δ olduğunu kabul edersek,
∆m ≈ δ∆V
(121)
yazabiliriz. Şimdi bütün cismin bir noktaya yoğunlaştını ve bu noktanın
koordinantlarının
x̃∆m,
ỹ∆m,
z̃∆m
(122)
koşulunu sağladığını varsayalım. ∆V → 0 iken, () ifadelerinden, koordinat
düzlemlerine göre cismin momentlerini yazabiliriz:
Z
Z
Z
M y z = x̃d m, M zx = ỹd m,
M x y = z̃d m
Buradan , kütle merkezinin koordinatlarını yazabiliriz:
R
R
R
x̃d m
ỹd m
z̃d m
x= R
, y= R
, z= R
dm
dm
dm
(123)
(124)
Düzlemsel Bölgelerin Kütle Merkezi
Tanım 0.49. Düzlemsel bir bölgenin kütle merkezi, bütün noktalarının
konsantre olduğu kabul edilen (x, y) noktasıdır.
Düzlemsel bir A bölgesinin (x, y kütle merkezi
Z
M y = x A = xd A
Z
M x = y A = yd A
(125)
(126)
(127)
eşitliklerini sağlar. Bu eşitliklerden
R
xA =
yA =
xd A
R A
yd A
A
bağıntıları çıkarılır.
Ağırlık Merkezi Bulma Problemleri
Mekanikte bir cismin kütle merkezi (ağırlık merkezi), cismin bütün
noktalarının konsantre olduğu bir noktadır.
(128)
(129)
59
60
CALCULUS
1. x32 + y 2 = 25 çemberinin sınırladığı diskin ikinci dörttebirlik böldede
(second quadrant) kalan kısmının ağırlık merkezini bulunuz.
Çözüm:
A=
π 2 25
5 =
π
4
4
(130)
Z 0 p
4
20
x 25 − x 2 d x = −
25π −5
3π
Z 0 q
4
20
y=
y 25 − y 2 d x = −
25π −5
3π
x=
(131)
(132)
(133)
olur.
2. x 2 + y 2 = a 2 ile sınırlı birim diskin birinci dörtte birlik bölgede (first
quadrant) kalan kısmının kütle merkezini bulunuz.
Çözüm:
Yoğunluğun her yerde aynı ve olduğunu varsayalım δ = 1 olur.
d m = δd A
q
= a2 − y 2 d y
Z
a
Mx =
y dm
Z0 a q
y a2 − y 2 d y
=
0
Z
q
−1 a
=
(−2y) a 2 − y 2 d y
2 0
µq
¶ 3 ¯¯a
2¯
−2
=
a2 − y 2 ¯
¯
3(2)
0
1
= a3
3
y=
Mx
A
=
a3
3
πa 2
4
=
4a
3π
x=
My
A
4a
=
3π
simetri nedeniyle
FIZIKSEL UYGULAMALAR
3. y = h 2 − x 2 parabolü ile Ox−ekseni arasında kalan bölgenin kütle
merkzini bulunuz.
Çözüm:
Z Z
Mx =
dA
Z
=
=
R
+h Z h 2 −x 2
ydy
−h 0
Z +h
1
−h
2
(h 2 − x 2 )2 d x
8 5
h
15
=
Z Z
A=
dA
R
+h Z h 2 −x 2
Z
y d yd x
=
Z
=
−h 0
+h
(h 2 − x 2 ) d x
−h
¯
1 ¯h
= h 2 x − x 3 ¯¯
3
−h
4 3
= h
3
Mx
A
2h 2
=
5
y=
Z Z
xd A
My =
R
+h Z h 2 −x 2
Z
x d yd x
=
Z
=
−h 0
+h
−h
x(h 2 − x 2 ) d x
==
x=
My
A
0
=
A
=0
4. Birim kareden birim disk çıkarılıyor. Geri kalan üçgen benzeri düzlemsel bölgenin ağırlık merkezini bulunuz.
Çözüm:
61
62
CALCULUS
Birim kareyi koordinat eksenind x = 1, y = 1 doğruları ile koordinat
eksenlerinin sınırladığı düzlemsel bölgedir. Birim disk x 2 + y 2 = 1
çemberi ve içidir. Şekilden birim kareden birim disk atılınca kalan
bölge görülüyor.
Problemi daha genel tutmak içim 1 yerine a alalım.
Z Z
Mx =
yd A
Z a RZ a
=
y d yd x
p
0
a 2 −x 2
Z a
¡ 2
¢
1
=
a − (a 2 − x 2 ) d x
2 0
Z
1 a 2
x dx
=
2 0
1
= a3
6
aZ a
Z
A=
p
0
a 2 −x 2
d yd x
π 2
a
4
a 2 (4 − π)
=
4
= a2 −
Mx
A
a3
4
=
6 a 2 (4 − π)
2a
=
12 − 3π
y=
Simetri nedeniyle,
x=
2a
12 − 3π
olur.
5. y = si nx, 0 ≤ x ≤ π ile Ox− ekseni arasında kalan düzlemsel bölgenin
ağırlık merkezini bulunuz.
Çözüm:
Z Z
Mx =
yd x
R
πZ
Z
=
si nx
(yd y)d x
0
0
π
1
si n 2 x d x
2 0
Z
1 π
=
(1 − cos2x) d x
4 0
1
1
= π − si n2π
4
8
1
= π
4
Z
=
FIZIKSEL UYGULAMALAR
Z Z
A=
yd A
R
π Z si nx
Z
=|
d y d x|
Z0 π
0
si nx d x|
=|
0
= |cosx|π0 |
= | − 1 − 1|
=2
Mx
A
1
= π
8
My
x=
A
1
= π
2
y=
simetri nedeniyle
Alıştırmalar
Aşağıda verilen eğrilerle sınırlanmış düzlemsel bölgelerin kütle merkezlerini bulunuz.
( 95 , 95 )
1. y 2 = 4x, x 2 = 4y;
1 e+1
( e−1
, 4 )
2. y = e x , x = 0, x = 1, y = 0;
(πa, 5a
6 )
3. x = a(θ − si nθ), y = a(1 − cosθ);
4. x = asi nθ, y = acosθ;
4a
( 4a
3i , 3i )
Yay’ın Kütle merkezi
Düzlemsel bölgenin kütle merkezine benzer olarak bir yay’ın kütle
merkezi tanımlanabilir:
Z
M y = sx =
xd s
Z
Mx = s y =
yd s
Örnek:
p
y = a 2 − x 2 , a > x, x > 0 yayının kütle merkezini bulunuz.
Çözüm:
Z
Mx = y s = y
a
Z
ds = ya
y=
0
p
dx
a2 − x2
y asi n
2a
π
x =0
simetri
¯a
¯
y aπ
=
a ¯0
2
−1 x ¯
63
64
CALCULUS
Alıştırmalar
Aşağıdaki yayların kütle merkezlerini bulunuz:
1. x = 3t 2 , y = 6t , 0 ≤ t ≤ 2
2. x = e −t cost , y = e −t si nt , 0 ≤ t ≤ 2π
3. x = e y , 0 ≤ y ≤ 1
4. x = asi n 3 t , y = acos 3 t
5. y = coshx, −1 ≤ x ≤ 1
Yoğunluk
Bir cismin P noktasını içeren küçük bir elementini ∆V ile ve ∆V nin
kütlsini ∆m ile gösterlim. Eğer
∆m
∆V t o0 δV
δ = lim
(134)
limiti varsa, buna cismin P noktasındaki yoğunluğu denilir. Bu tanımdan
anlaşıldığı gibi, bir cismin yoğunluğu sabit olmayabilip her noktada farklı
bir yoğunluğa sahip olabilir. Tabii, bazı cisimlerde yoğunluk her noktada
aynı olabilir. (134) limitini
δ=
dm
dV
dersek,
d m = δdV
(135)
biçiminde de yazabiliriz. Şimdi bir cismin kütlesi ∆m olan çok küçük
∆V parçacıklarına ayrıldığını varsayalım. Her parçacığın içerdiği P
noktasındaki yoğunluğun δ olduğunu kabul edersek,
∆m ≈ δ∆V
(136)
yazabiliriz. Şimdi bütün cismin bir noktaya yoğunlaştını ve bu noktanın
koordinantlarının
x̃∆m,
ỹ∆m,
z̃∆m
(137)
koşulunu sağladığını varsayalım. ∆V → 0 iken, () ifadelerinden, koordinat
düzlemlerine göre cismin momentlerini yazabiliriz:
Z
Myz =
Z
x̃d m,
M zx =
Z
ỹd m,
Mx y =
z̃d m
(138)
Buradan , kütle merkezinin koordinatlarını yazabiliriz:
R
x= R
x̃d m
dm
R
,
y= R
ỹd m
dm
R
,
z= R
z̃d m
dm
(139)
Örnek 0.50. r yarıçaplı bir çember, çember düzleminde ve çember
merkezine b, (b > r ) uzaklıkta sabit duran bir eksen etrafında döndürülüyor.
Meydana gelen cismin (simit, torus, daughnut) yüzey alanını ve hacmini
bulunuz.
FIZIKSEL UYGULAMALAR
Çözüm:
Çemberin ağırlık merkezi kendi merkezidir. Çemberin merkezi eksen
etrafında bir dönüş yapınca 2πb kadar yol alır. Çemberin alanı πr 2 dir.
Pappus teoremine göre hacim
V = (2πb)(πr 2 ) = 2π2 br 2
olur, yüzey alanı ise
S = (2πb)(2πr ) = 4π2 br
olur.
65
Üç Katlı İntegraller
Üç katlı ya da n-katlı integral tanımı iki katlı integralin genellemesidir.
Bu bölümde üç katlı integralleri iele alacağız. İki katlı intgralde integral
Figure 47: Üç katlı integral
bölgesi olarak düzlemdel bir D blgesini alıyorduk. Üç katlı integralde,
integral bölgesi düzlemsel olmak yerine üç boyutlu uzayda bir T hacmi
olacaktır. w = f (x, y z) fonksiyonunun tanım bölgesi
T = {(x, y, z)| w = f (x, y, z), a ≤ x ≤ b, c ≤ y ≤ d , e ≤ z ≤ f , x, y, z ∈ R}
kümesidir. Bazı yerlerde ≤ yerine < bağıntısı gelebilir. Tabii bu küme
bir dikdörtgenler prizmasıdır. Ama bu özel bir durumdur; T her zaman
uzayda bilinen bir geometrik şekle benzemeyebilir. T kümesi üç boyutlu
uzayda bir yer (hacim) doldurur. Bu hacme katı cisim (solid) denilir.
Üç katlı interali tanımlamak için, ilk işimiz T tanım kümesinin
bir bölüntüsünı oluşturmak olacaktır. Tek katlı integralde bir doğru
parçasının ,iiki katlı integralde bir dikdörtgenin bölüntüsünı oluşturmuştuk. Üç katlı integralde ise bir dikdörtenler prizmasının bölüntüsünı
oluşturacağız. Bu iş, önce yaptıklarımızın bezeri oacaktır:
[a, b] aralığının bir bölüntüsü n tane alt aralıktan oluşan
P = a = x 0 < x 1 < x 2 < x 3 < . . . < x n−1 < x n = b,
n ∈ N+
[c, d ] aralığının bir bölüntüsü m tane alt aralıktan oluşan
Q = c = y 0 < y 1 < y 2 < y 3 < . . . < y m−1 < y m = d
m ∈ N+
[e, f ] aralığının bir bölüntüsü s tane alt aralıktan oluşan
R = e = z 0 < z 1 < z 2 < z 3 < . . . < z s−1 < z s = f
s ∈ N+
olsun. T hacminin aytrışımını
Ti j k = P × Q × R
Figure 48: Katı cismin bölüntüsü
= [x i −1 , x i ] × [y j −1 , y j ] × [z k−1 , z i ]
1 ≤ i ≤ I, 1 ≤ j ≤ J, 1 ≤ k ≤ K ,
I , J , K ∈ N+
biçiminde ifade edebiliriz. İnteral tanımında bölüntü aralıklarının en
uzununun uzunluğu sıfıra giderken limit alındığı için, her üç boyuttaki
bölüntü aralıklarını kendi aralarında eşit almak bir kısıtlama getirmez.
Simgeleri basitleştirmek için, P bölüntüsündeki aralıkların uzuluklarının
aynı ve ∆x, Q bölüntüsündeki aralıkların uzuluklarının aynı ve ∆y, R
Figure 49: Bir bölüntünün hacmi
68
CALCULUS
bölüntüsündeki aralıkların uzuluklarının aynı ve ∆z olduğunu varsayalım. Buna göre T prizmasının Ti j k küçük prizmalarından oluştuğunu ve
onların her birisinin hacminin
∆V = ∆x × ∆y × ∆z
(140)
olduğunu söyleyebiliriz. Artık integral tanımı için Riemann toplamını
oluşturabiliriz:
(x i∗j k , y i∗j k , z i∗j k ) ∈ Ti j k
olmak üzere
n X
m X
s
X
S nms =
i =1 j =1 k=1
f (x i∗j k , y i∗j k , z i∗j k )∆V
(141)
diyelim.
Tanım 0.51. T bölgesi üç boyutlu R3 uzayında bir bölge ve f (x, y, z)
fonksiyonu bu bölge üzerinde tanımlı bir fonksiyon olsun.
n X
m X
s
X
Ñ
T
f (x, y, z)dV =
lim
n,m,s→∞
i =1 j =1 k=1
f (x i∗j k , y i∗j k , z i∗j k )∆V
(142)
diyelim. Sağdaki limit varsa, bu limit değerine f fonksiyonunun T bölgesi
üzerindeki üç katlı integrali denilir ve soldaki simge ile gösterilir.
Anımsanacağı gibi, iki katlı integrali tanımında hesaplamanın zorluğunu aşmak için, katlı integraliintegral tanımından hesaplamak yerine
ardışık integrallerle hesaplama yoluna gitmiştik. Benzer düşünceyi üç
katlı integrallere de uygulayacağı. Üç katlı integrali art arda uygulanan
üç tane tek katlı integralin hesplanmasına indirgeyebiliriz. O durumda,
tek katlı integral için bildiğimiz bütün integral alma yöntemlerini uygulayabileceğiz. Bu olgu Kaatlı integrallerin hepsi için geçerlidir ve integral
hesabını çok kolaylaştırır.
Yine anımsayacağınız gibi, düzlemsel bir D bölgesi üzerinden iki katlı
integrali ardşık integrallere dönüştürüken D bölgesinin Ox− ve O y−
eksenleri üzerine izdüşümlerini alıyor ve izdüşümün uç noktalarını en
dıştaki integralinsınırları olark kullanıyorduk. Benzer işi üç boyut için
de düşünebiliriz.Ancak, bu kz izdüşümler koordinat eksenlei yerine x y,
xz, y z koordinat düzlemleri üzerine yapılacaktır. Bu üçünü ayrı ayrı bir
teorem halindeyazalım:
Theorem 0.52.
1. x y koordinat düzlemine izdüşüm:
f (x, y, z) fonksiyonu
T x y = {(x, y, 0)| (x, y, z) ∈ T , g 1 (x, y) ≤ z ≤ g 2 (x, y)}
Figure 50: xy düzlemine izdüşüm
bölgesi üzerinde sürekli ise,
Ñ
T
eşitliği sağanır.
Ï
f (x, y, z)dV =
µZ
g 2 (x,y)
¶
f (x, y, 0) d z d A
Tx y
g 1 (x,y)
(143)
Ü Ç K AT L I I N T E G R A L L E R
69
2. xz koordinat düzlemine izdüşüm:
f (x, y, z) fonksiyonu
T xz = {(x, 0, z)| (x, y, z) ∈ T , h 1 (x, z) ≤ z ≤ h 2 (x, z)}
mine izdüşüm
bölgesi üzerinde sürekli ise,
Ñ
T
h 2 (x,z)
µZ
Ï
f (x, y, z)dV =
T xz
¶
f (x, 0, z) d y d A
(144)
h 1 (x,z)
eşitliği sağanır.
3. xz koordinat düzlemine izdüşüm:
f (x, y, z) fonksiyonu
Figure 52: yz düzlemine izdüşüm
T y z = {(0, y, z)| (y, z) ∈ T , k 1 (y, z) ≤ z ≤ k 2 (y, z)}
bölgesi üzerinde sürekli ise,
Ñ
µZ
Ï
T
f (x, y, z)dV =
T xz
k 2 (y,z)
¶
f (0, y, z) d y d A
(145)
k 1 (y,z)
eşitliği sağanır.
Hacim
T tanım bölgesine f (x, y z) ≡ 1 ise, f nin T blgesi üzeinden ç katı interali
T katı cisminin hacmine eşitir. Bunu bir teoremolarak ifade edbiliriz:
Theorem 0.53.
Ñ
T
µZ
Ï
f (x, y, z)dV =
Tx y
Ï
=
¡
g 2 (x,y)
¶
f (x, y, 0) d z d A
(146)
g 1 (x,y)
¢
g 2 /x, y) − g 1 (x, y) d A
(147)
ifadesi iki yüzey araasında kalan katı cismin hacmini verir.
Örnek 0.54. T katı cismi x = 0, y = 0, z = 0, x4y + z = 1 düzlemlerinin
sınırladığı düzgün dörtyüzlüdür.
Ñ
zdV
(148)
T
integralini hesaplayınız.
Çözüm: T bölgesinin x y düzlemi üzeeine izdüşümü T x y olsun. T
bölgesi üstten z = 1 − x − y düzlemi ile ve alttan z = 0 düzlemi ile sınırlıdır:
T = {(x, y, z) :
0 ≤ x ≤ 1, 0 ≤ y ≤ 11 − x, 0 ≤ z ≤ 1 − x − y}
(149)
Figure 53: Düzgün dörtyüzlü
70
CALCULUS
dir. O halde,
Z 1Z
Ñ
zdV =
T
1−x Z 1−x−y
zd zd yd x
0
0
Z 1Z
=
=
=
=
=
=
=
0
0
¯
1−x z 2 ¯1−x−y
¯
2 ¯0
0
d yd x
¯1−x−y
Z Z
1 1 1−x z 2 ¯¯
d yd x
2 0 0
2 ¯0
Z 1 Z 1−x
1
(1 − x − y)2 ; d yd x
2 0 0
¯1−x
Z
1 1 (1 − x − y)3 ¯¯
dx
−
¯
2 0
3
0
Z 1
1
(1 − x)3 d x
6 0
¯1
µ
1
(1 − x)4 ¯¯
−
¯
6
4
0
1
24
Ödev
Aynı integrali T nin xz ve y z düzlemlei üzerine izdüşümleri için
hesaplayınız.
Örnek 0.55. T katı cismi z = 8 − x 2 − y 2 , z = x 2 + y 2 paraboloidleri arısında
kalan bölgedir.
Ñ
dV
(150)
T
integralini T nin xz düzlemi üzerine izdüşümü (2.Tip) ve xz düzlemi
üzerine izdüşümü (3.Tip) üzerinde hesaplayınız.
Çözüm: xy-düzlemi üzerindeki izdüşümü T x y = x 2 + y 2 = 4 diskidir.
Çünkü z = 8 − x 2 − y 2 denkleminde z = 0 konulursa T x y izdüşümü
Figure 55: paraboloid
x 2 + y 2 = 4 olur. Buradan
Ñ
I=
Z
dV
T
0
p
4−x 2
Z
Z
8−x 2 −y 2
p
−2 − 4−x 2 x 2 +y 2
p
4−x 2 ¡
Z 2Z
=4
=
2
d zd yd x
¢
8 − 2(x 2 + y 2 ) d yd x
0
= 16π
olur. Ayrıca,
Z 4 Z 4 Z pz−y 2
Figure 56: paraboloid
I=
p
y2 −
0
z−y 2
2
Z
d xd zd y +
p
8−y 2 Z
Z
8−z−y 2
d xd zd y
p
−2 4
−
8−z−y 2
Z
p
8−z−x 2
ya da
Z 4Z
I=
p
z
p
Z
z−x 2
p
p
− z − z−x 2
0
p
8−z
Z 8Z
d xd zd y +
p
p
− 8−z − 8−z−x 2
4
d xd yd z
ve
Figure 57: paraboloid
Z
I=
2
Z 4Z
p
z−x 2
p
−2 x 2 − z−x 2
Z
d yd zd x +
2
Z
−2 4
8−x 2 Z
p
8−z−x 2
p
− 8−z−x 2
d yd zd x
Ü Ç K AT L I I N T E G R A L L E R
ya da
Z 4Z
I=
0
p
z
p
Z
z−x 2
p
p
− z − z−x 2
Z 8Z
d yd xd z +
4
p
8−z
Z
p
8−z−x 2
p
p
− 8−z − 8−z−x 2
d yd xd z
olur.
Üç KAtlı İntegrallerde Değişken Değiştirme
Tek ve iki katlı inegrallerde yaptığımız gibi, üç katlı integral alırken de
hesaplamayı kolaylaştıracak değişken değiştirimi yapabiliriz. Bunu
sağlayan teorem şudur:
Theorem 0.56. 1.
φ = f (x, y, z) fonksiyobu üç boyutlu uzaydaki bir S hacmi bölgesinde
sürekli, bire bir ve örten τ dönüşümü,



x = g (u, v, w)


τ : y = h(u, v, w)



z = k(u, v, w)
S bölgesini S ∗ bölgesine dönüştürsün.
g , h, k fonksiyonları S ∗ üzerinde sürekli türevlenebilir olsunlar.
τ dönüşümünün jacobian’ı
¯¯
¯¯ x u
∂(x, y, z) ¯¯¯¯
J (u, v, w) =
= ¯¯ y u
∂(u, v, w) ¯¯¯¯
zu
xv
yv
zv
¯¯
x w ¯¯¯¯
¯¯
y w ¯¯
¯¯
z w ¯¯
olmak üzere J (u, v, w) 6= 0 ise
Ñ
Ñ
S
f (x, y, z)dV =
S∗
¡
¢
f g (u, v, w), h(u, v, w), k(u, v, w) |J (u, v, w)| d ud vd w
olur.
Kanıt: İki katlı integrallerde yaptığımıza benzer olarak yapılabilir.
Örnek 0.57. S = {(x, y, z)| 1 ≤ x ≤ 2, 0 ≤ x y ≤ 2, 0 ≤ z ≤ 1} olmak üzere,


u = x


τ : v = xy



w = 3z
dönüşümü altına
Ñ
S
integralini hesaplayınız.
(x 2 y + 3x y z) d xd yd z
71
72
CALCULUS
Çözüm: u = x, v = x y, w = 3z ⇒ x = u, y = uv , z =
Ñ
S
w
3
yazılablir. Buradan,
(x 2 y + 3x y z) d xd yd z
³
v w ´
v
u 2 ( ) + 3u( )( ) |J (u, v, w)| d ud vd w
u
u 3
S∗
Z Z Z
1 3 2 2
vw
(v +
d ud vd w
3 0 0 1
u
¯2
Z Z
v2 ¯
1 3 2
(1 + w ln 2) ¯¯ d w
3 0 0
2 o
Z
1 3
(1 + w ln 2) d w
3 0
µ
¶
w2
2
(w +
ln 2
3
2
2
(2 + 3 ln 2)
3
Ñ
=
=
=
=
=
=
= 2 + ln 8
bulunur.
Alıştırmalar
1. x = uv, y = v w, z = uv dönüşümünün Jacobiyanını bulunuz.
2. x = e u−v , y = d u+v , z = e u+v+w dünüşümünün Jacobiyanını bulunuz.
3. S :
x2
4
2
2
+ x4 + x4 = 1 elipsoidinin sınırladığı bölgenin hacmini x = 2u, y =
3v, z = 5w dönüşümünü kaullanarak hesaplayınız.
Silindirsel Koordinatlar
Üç boyutlu uzayda bir (x,y,z) noktasının dikey kartezyen koordinat
sisteminden silindirsel koordinatlara dönüşümü,



x = r cos θ


3
3
τ : R → R y = r sin θ



z = z
denklemleri ile verilir.
Silindirsel koordinatlar kullanılarak üç katlı integraller kolayca hesaplanabilir.
Örnek 0.58. x 2 +y 2 = a 2 denklemini silindirsel koordinatlsra dönüştürünüz.
Figure 58: Siindirsel koordinatlar
Çözüm:
Dikey kartezyen koordinat sisteminde silindirsel koordinat sisatemine
Figure 59: Kartezyenden silindirsele dönüşüm
dönüşüm formülleri kullanılırsa,
q
y
r = x 2 + y 2 ⇒ tan θ = , z = z
x
çıkar.
Örnek 0.59. x 2 + y 2 = a z paraboloidini silindirsel koordinatlara
dönüştürünüz.
Ü Ç K AT L I I N T E G R A L L E R
73
Çözüm:
Dikey kartezyen koordinat sisteminde silindirsel koordinat sisatemine
dönüşüm formülleri kullanılırsa,
V=
çıkar.
Silindirsel kootlilardaki üç katlı integrali ardışık integrallere dönüştürmk
için şu teoremi kullanırız:
Theorem 0.60. T cismi üstten z = v(t , θ) v3 alttan z = u(r , θ) yüzeyleri le
sınırlı olsun.
1. T nin x y− düzlemi üzerine D izdşümü kutupsal koordinatlarda
verilsin.
2. f (x, θ, z) fonksiyonu S üzerinde sürekli olsun.
3.
¯¯
¯ ¯¯ x
¯
¯ ∂(x, y, z) ¯ ¯¯¯¯ r
¯ = ¯¯ y r
r = ¯¯
∂(r , θ, z) ¯ ¯¯¯¯
zv
xθ
yθ
zθ
¯¯ ¯¯
x z ¯¯¯¯ ¯¯¯¯cos θ
¯¯ ¯¯
y z ¯¯ = ¯¯ sin θ
¯¯ ¯¯
z z ¯¯ ¯¯ 0
−r sin θ
r cos θ
0
¯¯
0¯¯¯¯
¯¯
0 ¯¯
¯¯
1 ¯¯
ise,
Ñ
S
f (r , θ, z)dV =
Ï Z
v(r ,θ
D u(r ,θ
f (r , θ, z)r d zd r d θ
(151)
eşitliği sağlanır.
Kanıt: Öncekiler gibi yapılabilir.
Özel olarak,
D = {(r , θ) :
α ≤ θβ, h 1 (θ) ≤ r ≤ h 2 (θ)}
Figure 60: x y düzlemine izdüşüm
ise,
Ñ
S
f (r , θ, z)dV =
Ï Z
bet a
Z
h 2 (θ) Z v(r ,θ)
D al pha h 1 (θ)
u(r ,θ)
f (r , θ, z)r d zd r d θ
(152)
olur.
Örnek 0.61. S bölgesi birinci sekizde birlik (first octant) bölgde x 2 + y 2 = 1
ve x 2 + y 2 = 4 silindirleri ile z = 0, z = 1, x = 0, x = y düzlemleri tarafından
sınırlı bölge ise,
Ñ
S
(x 2 + y 2 )dV
(153)
integralini hesaplayınız.
Çözüm:
S = {(x, y, z) :
−2 ≤ 2. −
p
4 − x2 ≤ y ≤
p
4 − x2,
q
x 2 + y 2 ≤ z ≤ 2}
Figure 61: İzdüşüm
74
CALCULUS
olduğundan,
Ñ
S
(x 2 + y 2 )dV
2π Z 2 Z 2
Z
=
0
2π Z 2
Z
=
0
Z
r
0
0
2π Z 2
r 2 r d zd r d θ
¯2
r 3 z ¯r d r d θ
r 3 (2 − r )d r d θ
¯
µ
1 ¯2
1
= 2π r 4 − r 5 ¯¯
2
5 0
16
=
π
5
=
0
0
x 2 + y 2 = 1, 0 ≤ z ≤ 1} ise
Ñ
2
2
ze −x −y dV
Örnek 0.62. S = {(x, y, z) :
(154)
S
integralini hesaplayınız.
Çözüm: Silindirik koordinatlar kullanılır ve ardılık integraller uygulanırsa,
Ñ
ze −x
2 −y 2
dV
S
Z 1Z
2π Z 1
=
0 0
µ
¶0
π
1
=
1−
2
e
2
ze −r r d r d θd z
çıkar.
Örnek 0.63. S cismi 8 − r 2 ve z = r 2 paraboloidleri ile sınırlı bölge ise S
cisminin hacmini bulunuz.
Çözüm: Hacim formülüuygulanırsa,
2π Z 2 Z 8−r 2
Z
V=
Figure 62: x y düzlemine izdüşüm
0
=
r2
0
2π Z
Z
0
2
0
r d zd r d θ
(8 − r 2 − r 2 )r d r d θ
= 16π
bulunur.
Üç Katlı İntegrallerde Küresel Koordinatlar
Üç boyutlu uzayda bir P (x, y, z) noktasının dikey kartezyen koordinat
sisteminden küresel koordinatlardaki (ρ, φ, θ) noktasına dönüştüren η
dönüşümü,
Figure 63: Küresel koordinatlar



x = ρ cos θ sin φ


3
3
η : R → R y = ρ sin θ sin φ



z = ρ cos φ
Ü Ç K AT L I I N T E G R A L L E R
75
denklemleri ile verilir. Burada P noktasının başlangıç noktasına uzaklığı
ρ, P noktasının x y− düzlemine izdüşümü olan Q noktasının başlangıç
noktasına uzaklığı r = ρ sin φ, OQ nun Ox− ekseniyle pozitif yöne yaptığı
açı θ (0 ≤ θ ≤ 2π), OP nin Oz− ekseni ile pozizitif yönde yaptığı açı
φ, (0 ≤ φ ≤ π) dır.
Örnek 0.64. Dikey kartezyen koordinat sistemindeki denklemi
x 2 + y 2 + (z − 1)2 = 1
olan küreyi küresel koordinat sisteminde gösteriniz.
Figure 64: Küresel koordinatlar
Çözüm: Yukrıdaki η dönüşümünü uygularsak,
1 = ρ 2 sin2 φ cos2 θ + ρ 2 sin2 φ sin2 θ + (ρ cos φ − 1)2
¡
¢
= ρ 2 sin2 φ cos2 θ + sin2 φ ρ 2 cos2 φ2ρ cos φ + 1
¡
¢
⇒= ρ 2 sin2 φ + cos2 φ
⇒ 2ρ cos φ
⇒ ρ 2 = 2ρ cos φ
⇒ ρ = 2 cos φ
çıkar.
Örnek 0.65. Dikey kartezyen koordinat sistemindeki denklemi
q
z = x2 + y 2
Figure 65: Dik dairesl koni1
olan koniyi küresel koordinat sisteminde gösteriniz.
Çözüm: Yukrıdaki η dönüşümünü uygularsak,
q
ρ cos φ = ρ 2 sin2 φ
(ρ ≥ 0, sin φ ≥ 0)
ρ cos φ = ρ sin φ
cos φ sin φ
φ=
π
4
(0 ≤ φ ≤ π)
çıkar.
Dikey kartezyen koordinat sistemindeki üç katlı integrali küresel
koordinat siteminde üç katlı integrale dönüştürmek için aşağıdaki
teoremi kullanırız:
Theorem 0.66. :
1. Küresel koordinatlarda gösteilen S sınırlı cismi üzerinde ξ = f (ρ, φ, θ)
fonksiyonu sürekli,
2. η dönüşümü geçerli,
3. η dönüşümünün Jacobiyanı,
¯¯
¯¯
¯
¯ ¯¯¯¯x ρ x φ x θ ¯¯¯¯
¯
¯
∂(x,
y,
z)
¯ = ¯¯¯¯ y ρ y φ y θ ¯¯¯¯
ρ 2 sin φ = ¯¯
¯¯
∂(ρ, φ, θ) ¯ ¯¯¯¯
z ρ z φ z θ ¯¯
¯¯
¯¯
¯¯sin φ cos θ ρ cos φ cos θ −ρ sin φ sin θ ¯¯
¯¯
¯¯
¯¯
¯¯
= ¯¯ sin φ sin θ ρ cos φ sin θ −ρ sin φ cos θ ¯¯
¯¯
¯¯
¯¯
¯¯ cos φ
−ρ sin φ
0
Figure 66: Dik dairesel koninin boyutları
76
CALCULUS
ise
Ñ
Ñ
S
f (x, y, z)dV =
S∗
f (ρ, φ, θ)ρ 2 sin φ d ρd φd θ
(155)
eşitliği sağlanır.
ı
3
Örnek 0.67. Üstten ρ ≤ 1 küresi ve alttan φ =
konisi ile sınırlı S böl-
gesinin hacmini bulunuz.
Çözüm:
Ñ
V=
Z
=
ρ 2 sin φd ρd φd θ
S
2π Z π/3 Z 1
0
0
0
ρ 2 sin φd φd θ
2π Z π/3
1
sin φd φd θ
3
¯π/3
Z 2π
¯
1
=
− cos φ¯¯ d θ
3
Z
=
0
0
0
0
1
= 2π
6
π
=
bi r i m 3
3
Örnek 0.68. S = {(x, y, z) :
x 2 + y 2 + z 2 ≤ 1} ise,
Ñ p
2
2
2 3
e (x +y +z ) dV
(156)
S
integralini hesaplayınız.
Çözüm:
S cismi küre olduğundan küresel koordinatları kullanamak kolaylık
sağlar. Üç katlı interali ardışık integrallere dönüştürüsek,
Ñ p
2
2
2 3
e (x +y +z ) dV
S
pi
Z
=
0
Z
2π Z 1
Z
0
pi
Z
e (ρ
2 )3
0
2π Z 1
ρ 2 sin φd ρd θd φ
3
e ρ ρ 2 sin φd θd φ
0
0
0
¯
µ
¯π
¡
1 ρ 3 ¯¯1
¯
= − cos φ 0 .2π e ¯
3
0
4
= π(e − 1)
3
=
Örnek 0.69.
p Z p
2
4−r 2
2ı Z
Z
0
0
0
3r d zd r d θ
integralini
1. Dikey katezyen koordinat istemine dönüştüünüz.
2. Küresel koordinat sistemine dönüştürünüz.
3. Silindirsel koordinat sistemine dönüştürerek hesaplayınız.
Çözüm:
(157)
Ü Ç K AT L I I N T E G R A L L E R
1.
Z p2−y 2 Z
p
2
Z
(4−x 2 −y 2 )
3d zd xd y
p
p
− 2 −
2.
2−y 2 (x 2 +y 2 )
2π Z π/4 Z 2
Z
0
0
3ρ 2 sin φd φd θ
0
3.
p Z p
2
4−r 2
2π Z
Z
0
0
0
3r d zd r d θ = 3
Z
=
Z
p
2¡
Z
+2π
0
2π
0
¢
r (4 − r 2 )1/2 − r 2 d r d θ
p
(8 − 4 2)d θ
0
p
= (8 − 4 22π
Alıştırmalar
Aşağıdaki interallerin integral bölgelerini çiziniz ve interali hesaplayınız.
1. (a)
π/2 Z 2 Z 9−r 2
Z
0
(b)
0
0
π/6 Z π/2 Z 3
Z
0
0
0
r d zd r d θ
ρ 2 sin φd ρd θd φ
2. S bölgesi z = 0 düzleminin üstünde, z 2 = 4x 2 + 4y 2 konisinin altında ve
yandan x 2 + y 2 = 1 sindiri ile sınırlı ise
Ñ
x 2 dV
S
integralini bulunuz.
3.
1
Z
Z
p
1−x 2
Z
2−x 2 −y 2
p
−1 − 1−x 2 x 2 +y 2
(x 2 + y 2 )d zd yd x
integralini silindirsel koordinatları kullanarak hesaplayınız.
4.
Z 1 Z p1−y 2 Z px 2 +y 2
0
x 2 +y 2
0
x y dV
integralini silindirsel koordinatları kullanarak hesaplayınız.
5.
Z
2
Z
p
4−x 2
Z p4−x 2 −y 2 q
z x 2 + y 2 + z 2 d zd xd y
p
−2 − 4−x 2 0
integralini hesaplayınız.
6.
Z 3 Z p9−y 2 Z p18−x 2 −y 2
0
0
p
x 2 +y 2
(x 2 + y 2 + z 2 ) d zd xd y
integralini hesaplayınız.
7. Birinci bölgede x 2 + y 2 + z 2 = 4 küresi ile sınırlı S bölgesi üzerinde
Ñ p
2
2
2
e x +y +z dV
S
integralini hesaplayınız.
77
Bibliography
Index
d A, 9
d xd y, 9
üç katlı integral, 67
hacim, 67
katlı integral, 9
iki katlı integral, 9
Riemann toplamı, 9
bölünrü, 9
katı cisim, 67
triple integral, 67