T.C. SELÇUK ÜNĠVERSĠTESĠ FEN BĠLĠMLERĠ ENSTĠTÜSÜ

T.C.
SELÇUK ÜNĠVERSĠTESĠ
FEN BĠLĠMLERĠ ENSTĠTÜSÜ
BULANIK DOĞRUSAL PROGRAMLAMA ĠLE
PORTFÖY OPTĠMĠZASYONU
Mehmet CEBECĠ
YÜKSEK LĠSANS TEZĠ
Endüstri Mühendisliği Anabilim Dalı
Nisan-2011
KONYA
Her Hakkı Saklıdır
ÖZET
YÜKSEK LĠSANS TEZĠ
BULANIK DOĞRUSAL PROGRAMLAMA ĠLE PORTFÖY OPTĠMĠZASYONU
Mehmet CEBECĠ
Selçuk Üniversitesi Fen Bilimleri Enstitüsü
Endüstri Mühendisliği Anabilim Dalı
DanıĢman: Doç. Dr. Turan PAKSOY
2011, 148 Sayfa
Jüri
Doç. Dr. Turan PAKSOY
Prof. Dr. Ahmet PEKER
Yrd. Doç. Dr. Nimet YAPICI PEHLĠVAN
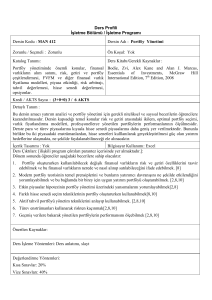
Portföy bir yatırımcının sahip olduğu menkul kıymetlerin listesidir. Portföy yönetimi ise
yatırımcının elindeki fonların, mevcut menkul kıymetler arasında minimum risk ve maksimum karlılığı
sağlayacak Ģekilde dağıtılmasıdır.
Bu çalıĢmada ilk olarak portföy yönetimi ile ilgili teorik bilgiler verilmiĢ, portföy seçim
modelleri üzerinde durulmuĢtur. Daha sonra bulanık mantık teorisi hakkında temel tanımlar verilmiĢ ve
bulanık doğrusal programlama yaklaĢımları üzerinde durulmuĢtur. ÇalıĢmanın son bölümünde Werners‟
ın geliĢtirdiği modele, Fiyat/Kazanç oranı ve Toplama-dağıtım endeksi kısıtları eklenmiĢ ve yeni bir
model oluĢturulmuĢtur.
Bu modelin LINDO 6.1 paket programı ile çözülmesi sonucu oluĢturulan portföy %7,43‟ lük bir
risk ve %4‟ lük beklenen getiri oranı sağlamaktadır.
VOB‟ da iĢlem gören opsiyonlu alım durumunun probleme katılması ile % 9,09‟ luk bir
beklenen getiri elde etmek mümkün olmaktadır.
Anahtar Kelimeler: Bulanık Doğrusal Programlama, Fiyat/Kazanç Oranı, Opsiyonlu Alım,
Portföy Seçimi, Toplama-Dağıtım Endeksi.
iv
ABSTRACT
MS THESIS
A FUZZY LINEAR PROGRAMMING APPROACH TO PORTFOLIO
OPTIMIZATION
Mehmet CEBECĠ
THE GRADUATE SCHOOL OF NATURAL AND APPLIED SCIENCE OF
SELÇUK UNIVERSITY
THE DEGREE OF MASTER OF SCIENCE
IN INDUSTRIAL ENGINEERING
Advisor: Assoc. Prof. Dr. Turan PAKSOY
2011,148 Pages
Jury
Assoc. Prof. Dr. Turan PAKSOY
Prof. Dr. Ahmet PEKER
Asst. Prof. Dr. Nimet YAPICI PEHLĠVAN
Portfolio is the list of securities that an investor owns. The portfolio management is the
distribution of funds that an investor owns between existing securities in a way to provide minimum risk
and maximum profit.
In this study, at first theoretical information on portfolio management is given and portfolio
selection models are studied. Then, basic definitions on fuzzy logic are made and fuzzy linear
programming approaches are briefly explained. Price/Earnings Ratio and Accumulation-Distribution
Index constraints added to model developed by Werners‟ and a new model was created
The portfolio created as a result of solving that model using LINDO 6.1, provides a risk with
7,43% and an expected return with 4%.
It is possible to obtain an expected return with 9,09% by adding call options proceeding in the
VOB to the problem.
Keywords: Fuzzy Linear Programming, Price/Earnings Ratio, Call Options, Portfolio Selection,
Accumulation-Distribution Index.
v
ÖNSÖZ
Bu çalıĢmanın amacı, bulanık doğrusal programlama yöntemini kullanarak hisse
senedi yatırımcıları için minimum risk ve maksimum karı sağlayacak olan optimal
portföyü oluĢturmaktır.
Bu amaç doğrultusunda, Ocak 2007-Aralık 2009 tarihleri arasında iĢlem gören
ve ĠMKB 30 endeksinde yer alan 30 hisse senedinin aylık getirileri, Toplama-dağıtım
endeksi değerleri, Fiyat/Kazanç oranı kullanılarak, bulanık doğrusal programlama ile
portföy seçimi modeline yeni kısıtlar eklenerek yeni bir model oluĢturulmuĢ ve LINDO
6.1 paket programı ile çözülmüĢtür. Önerilen bu modele ek olarak, Türkiye‟ de 2005
yılından bu yana faaliyet gösteren Vadeli ĠĢlem ve Opsiyon Borsası (VOB)‟ nda iĢlem
gören endeks sözleĢmesinin, opsiyonlu alım durumunda kazancı ve riski ne Ģekilde
değiĢtireceği sayısal bir örnekle açıklanmıĢtır.
Yüksek lisans öğrenimim boyunca bana vermiĢ olduğu emeklerden ve bu
çalıĢmanın gerçekleĢmesinde her türlü öğüt ve yardımlarıyla sağlamıĢ olduğu
katkılardan dolayı danıĢman hocam sayın Doç. Dr. Turan PAKSOY‟ a; çalıĢmamın her
aĢamasında değerli fikirlerinden yararlandığım sayın Yrd. Doç. Dr. Nimet YAPICI
PEHLĠVAN‟ a; kendi çalıĢmalarından vakit ayırıp yardımlarını esirgemeyen ArĢ. Gör.
Eren ÖZCEYLAN‟ a; lisans eğitimim boyunca bana vermiĢ oldukları emeklerden
dolayı Selçuk Üniversitesi Endüstri Mühendisliği Bölümü Hocalarıma; beni bugünlere
getiren, maddi ve manevi desteğini hiçbir zaman eksik etmeyen aileme saygılarımı ve
teĢekkürlerimi sunarım.
Bu çalıĢmanın portföy yönetimine ilgi duyan araĢtırmacılara yararlı olmasını
dilerim.
Mehmet CEBECĠ
KONYA-2011
vi
ĠÇĠNDEKĠLER
ÖZET .............................................................................................................................. iv
ABSTRACT ..................................................................................................................... v
ÖNSÖZ ........................................................................................................................... vi
ĠÇĠNDEKĠLER ............................................................................................................. vii
SĠMGELER VE KISALTMALAR .............................................................................. ix
1. GĠRĠġ ........................................................................................................................... 1
2. KAYNAK ARAġTIRMASI ....................................................................................... 2
3. MATERYAL VE METOT......................................................................................... 9
3.1. Materyal ................................................................................................................. 9
3.2. Metot ...................................................................................................................... 9
3.3. Portföy ve Portföy Yönetimi................................................................................ 10
3.3.1. Yatırım kavramı ............................................................................................ 10
3.3.2. Portföy tanımı ............................................................................................... 10
3.3.3. Portföy yönetimi ........................................................................................... 11
3.3.4. Portföy yönetimi süreci ................................................................................. 12
3.3.5. Portföy çeĢitleri ............................................................................................. 14
3.4. Yatırımlarla Ġlgili Riskler ve Yatırımın Getirisi .................................................. 15
3.4.1. Risk nedir? .................................................................................................... 16
3.4.2. Risk çeĢitleri ................................................................................................. 16
3.4.3. Risk ve getiri hesapları ................................................................................. 18
3.5. Fiyat/Kazanç Oranı .............................................................................................. 23
3.6. ĠĢlem Hacmi ile Getiri ĠliĢkisi .............................................................................. 27
3.7. Vadeli ĠĢlem ve Opsiyon Borsası ......................................................................... 30
3.7.1. Opsiyon iĢlemleri .......................................................................................... 30
3.7.2. Opsiyonların özellikleri ................................................................................ 31
3.7.3. Opsiyon sözleĢmelerinin türleri .................................................................... 32
3.7.4. Black & Scholes opsiyon değerleme modeli ................................................ 35
3.8. Portföy Seçim Teorileri ....................................................................................... 36
3.8.1. Geleneksel portföy yaklaĢımı ....................................................................... 36
3.8.2. Modern portföy yaklaĢımı ............................................................................ 37
3.8.3. Bulanık doğrusal programlama ile portföy seçimi yaklaĢımı ....................... 49
4. ARAġTIRMA SONUÇLARI VE TARTIġMA ...................................................... 76
4.1. Modelin Kurulması ve Çözülmesi ....................................................................... 76
4.2. Önerilen Modelin Opsiyonlu Alım Durumunda Değerlendirilmesi .................... 82
5. SONUÇLAR VE ÖNERĠLER ................................................................................. 88
vii
KAYNAKLAR .............................................................................................................. 90
EKLER .......................................................................................................................... 97
ÖZGEÇMĠġ ................................................................................................................ 148
viii
SĠMGELER VE KISALTMALAR
Kısaltmalar
DP : Doğrusal Programlama
BDP : Bulanık Doğrusal Programlama
F/K : Fiyat/Kazanç Oranı
HBK : Hisse BaĢına Kazanç
ADI : Toplama-Dağıtım Endeksi
B&S : Black & Scholes Opsiyon Değerleme Modeli
ĠMKB : Ġstanbul Menkul Kıymetler Borsası
VOB : Vadeli ĠĢlem ve Opsiyon Borsası
ix
1
1. GĠRĠġ
Portföy tek bir menkul kıymetten oluĢacağı gibi, birden fazla menkul kıymetin
bir araya getirilmesiyle de oluĢturulabilir. Burada önemli olan konu yatırımcının
tutumudur. Riski seven bir yatırımcı, riskin büyüklüğü ile doğru orantılı olan beklenen
getiri miktarını da arttırmaktadır. Fakat çoğu yatırımcı risk almaktan kaçınır. Bu Ģekilde
düĢünen bir yatırımcı için tek bir menkul kıymete yatırım yapmaktansa, çeĢitlendirme
yoluyla birden fazla menkul kıymete yatırım yapmak daha avantajlıdır.
Portföy yönetimi, süreklilik gösteren bir süreçtir. Çünkü bir taraftan ülkenin
içinde bulunduğu ekonomik durumun ve bu durum içerisinde yatırım araçlarının
dikkatli bir Ģekilde takip edilmesi gerekmektedir. Bunun dıĢında, yatırımcı (kurumsal
veya bireysel), elinde bulunan imkanlar ve amaçlar arasında optimum bir denge
kurarak, bu dengenin devamlılığını sağlamak zorundadır.
Bu çalıĢmanın temel amacı, ĠMKB 30 endeksinde iĢlem gören hisse senetlerini
esas alarak, yatırımcıların getirilerini maksimum, risklerini ise minimum yapmaktır. Bu
amaç kapsamında Werners‟ ın geliĢtirdiği bulanık doğrusal programlama modeline
Fiyat/Kazanç oranı ve Toplama-dağıtım endeksi kısıtları eklenerek yeni bir model
oluĢturulmuĢtur.
ÇalıĢmanın ikinci bölümünde, bulanık doğrusal programlama, Fiyat/Kazanç
oranı, Toplama-dağıtım endeksi konularında daha önce yapılmıĢ olan çalıĢmalara
değinilmiĢtir.
ÇalıĢmanın üçüncü bölümünde, metot ve materyaller açıklanmıĢ, portföy ve
portföy yönetimi hakkında bilgiler verilmiĢtir. Ayrıca portföy seçim teorileri
açıklanarak, portföy optimizasyonunda bulanık mantık yaklaĢımını kullanan üç temel
model incelenmiĢtir.
ÇalıĢmanın dördüncü bölümünde, geliĢtirilen modelin çözüm aĢaması yer
almaktadır. Buna ek olarak, Vadeli ĠĢlem ve Opsiyon Borsası‟nda opsiyonlu alım
durumu kullanılarak risk ve getiri değiĢimini gösteren sayısal bir örnek çözülmüĢ ve
sonuçlar karĢılaĢtırılmıĢtır.
2
2. KAYNAK ARAġTIRMASI
Kaynak araĢtırması dört ana baĢlık altında incelenmiĢtir. Bunlar;
i. Bulanık doğrusal programlama (BDP) ile ilgili kaynak araĢtırması,
ii. Bulanık portföy seçimi ile ilgili kaynak araĢtırması,
iii. Fiyat/Kazanç oranı ile ilgili kaynak araĢtırması,
iv. ĠĢlem hacmi-getiri iliĢkisi ile ilgili kaynak araĢtırmasıdır.
i. Bulanık doğrusal programlama (BDP) ile ilgili kaynak araĢtırması;
Zimmermann (1974), bulanık doğrusal programlama ile yapılan ilk çalıĢmadır.
Bulanık küme teorisini ilk defa bir optimizasyon probleminde kullanmıĢtır.
Negoita (1981), bulanık katsayılarla, bulanık doğrusal programlama problemini
formüle etmiĢ ve Robust programlama modeli olarak adlandırmıĢtır.
Chanas (1983), bulanık kısıtlayıcıların belirlediği uygun çözüm alanının bilgi
eksikliği yüzünden, amaç fonksiyonuna iliĢkin eriĢim düzeyi ile tolerans miktarının
karar verici tarafından baĢlangıçta belirlenemeyeceğini öne sürmüĢtür. Bulanık amaç
fonksiyonlu ve bulanık kısıtlayıcılı doğrusal programlama problemleri için parametrik
programlama sonrası karar verici tercihini dikkate alan bir çözüm yaklaĢımı önermiĢtir.
Nakamura (1984), amaçların üçgensel üyelik fonksiyonları ile temsil edildiği
çok amaçlı doğrusal programlama modellerini, parçalı üyelik fonksiyonlu bulanık
doğrusal programlama modellerine dönüĢtürerek çözmüĢtür.
Tanaka ve Asai (1984), teknoloji matrisi ve amaç fonksiyonu katsayılarını,
kısıtların sağ taraf sabitlerini bulanık sayılar olarak alıp, bunları bulanık fonksiyonlar
olarak kullanmıĢlardır.
Verdegay (1984), bulanık kısıtlayıcı bir doğrusal programlama modelinin
çözümünün bulanık bir küme ile temsil edilmesi gerektiğini öne sürmüĢtür.
Carlsson ve Korhonen (1986), tüm parametreleri tam olarak bilinmeyen bulanık
doğrusal programlamaya, parametrik bir yaklaĢımda bulunmuĢlardır.
Werners (1987), amaç fonksiyonuna iliĢkin üyelik fonksiyonunun analist
tarafından belirlenebileceğini vurgulamıĢtır. Werners‟ a göre kısıtların üyelik
fonksiyonları karar verici tarafından belirlenirken, kısıtların bulanık olması nedeniyle
amaç fonksiyonuna iliĢkin üyelik fonksiyonu karar verici tarafından önceden
belirlenemez.
3
Delgado ve ark. (1989), hem bulanık sayı hem de bulanık kısıtlar kümesini
içeren genel bir bulanık doğrusal programlama modeli sunmuĢ ve bu modeli çözmek
için yeni bir yaklaĢım üzerinde çalıĢmıĢlardır.
Rommelfanger ve ark. (1989), amaç fonksiyonunda bulanık parametrelerle
doğrusal programlama problemlerini çözmek için yeni bir yöntem sunmuĢlardır.
Zimmermann (1991), karar vericinin ulaĢmak istediği amaç fonksiyonunun
değeri için bir istek seviyesinin kurulabileceğini ve kısıtların her birinin bir bulanık
küme olarak modellenebileceğini öne sürmüĢtür.
Shaocheng (1994), aralık sayılar ve bulanık sayılarla, bulanık doğrusal
programlama üzerinde çalıĢmıĢ ve bulanık kısıtlı doğrusal programlama problemlerini
öncelikle amaç fonksiyonu için bir üst sınır belirleyerek bulanıklıktan kurtarmıĢtır.
Inuiguchi ve Sakawa (1998), bir bulanık amaç fonksiyonu ile doğrusal
programlama problemlerini yerleĢtirmede optimalliğin esnekliğini ve güçlülüğünü
(robust) ortaya koymuĢlardır.
Guu ve Wu (1999), iki aĢamalı bir yaklaĢım önermiĢlerdir. Bu yöntem, yalnız
amaç fonksiyonunun en yüksek üyelik derecesini araĢtırmakla kalmamakta, bunun
yanında her bir kısıt kaynağından en iyi Ģekilde yararlanmayı sağlamaktadır.
Jamison ve Lodwick (2001), problemde her bir sabit, bulanık sayı ile değiĢtirilip,
amaç ve kısıtlar olası kısıt bozulmaları için amacı cezalandırarak kısıtlanmamıĢ bulanık
bir fonksiyon olarak yeniden biçimlendirilmiĢtir.
Chiang (2001), BDP‟ yi formüle etmek için diğer çalıĢmalardan farklı olarak
istatistiksel veri ile istatistiksel güven aralığı kavramını kullanmıĢtır.
Gasimov ve Yenilmez (2002), doğrusal üyelik fonksiyonlarını kullanarak BDP
problemlerinin çözümünü yapmıĢlardır.
Sadeghi ve Hosseini (2004), enerji tedarik planlamasında BDP yöntemini
kullanmıĢlardır.
Amiri ve Nasseri (2007), trapez bulanık değiĢkenler ile doğrusal programlama
problemleri için bir dual simpleks metodu ve dualite sonuçları elde etmiĢlerdir.
Lotfi ve ark. (2009), bütün parametreleri ve değiĢkenleri üçgensel bulanık sayı
olan bulanık doğrusal programlama (FFLP) problemleri için bir farklı bir görüĢ öne
sürmüĢlerdir. Simetrik üçgensel bulanık sayılar ile ilgili var olan kavramları kullanarak
bulanıklığın miktarını durulaĢtırmak için bir çalıĢma yapmıĢlardır.
Fang ve ark. (2010), bulanık doğrusal programlama probleminin çözümü için
temel çizgi algoritması (the basic line algorithm) adı altında yeni bir model üzerinde
4
çalıĢmıĢlardır. Temel prensibi, Ģu anda kullanılan BDP çözümünün Simplex metodu ile
karĢılaĢtırılmasıdır. Temel çizgi algoritmasının avantajları sadece verilerin sabit ve
döngüye aykırı olması değildir. Bunlara ilave olarak bu model, problemin çözüm
adımlarını azaltarak üstünlüğünü göstermektedir.
Deng (2011), bulanık doğrusal programlama yaklaĢımını aralık değerli matrix
oyunlarını çözmek için kullanmıĢtır. Buradaki temel amaç, aralıklar ile matrix
oyunlarının sonuçlarını bulmada bulanık doğrusal programlama metodunu kullanmaktır.
Çünkü, matrix oyunlarının sonuçları aralıklı olarak ifade edilmektedir.
Matrix
oyununun değeri de bir aralığı ifade etmektedir.
ii. Bulanık portföy seçimi ile ilgili kaynak araĢtırması;
Östermark (1996), bulanık karar prensibini kullanarak, amaç değerlerini ve
kısıtları bulanık alarak bir dinamik portföy yönetim modeli geliĢtirmiĢtir.
Ramaswamy (1998), bulanık bir bono portföyü seçim modeli önermiĢtir.
Inuiguchi ve Ramik (1998), portföy seçimi problemi için stokastik programlama
ve matematiksel programlama yöntemlerini karĢılaĢtırmıĢ ve portföy seçimi için
matematiksel programlama yaklaĢımlarının avantaj ve dezavantajlarını belirtmiĢlerdir.
Parra (2001), portföy seçimi için bir hedef programlama yöntemi geliĢtirmiĢtir.
Buradaki portföy modeli, bulanık sayıların beklenen aralıklarına dayanmaktadır.
Ammar ve Khalifa (2003), bulanık portföy optimizasyonu için kuadratik
programlama yaklaĢımı kullanmıĢlardır.
Fang ve ark. (2005), bulanık karar teorisini kullanarak iĢlem maliyeleri yardımı
ile portföyü yeniden dengeleme çalıĢması gerçekleĢtirmiĢlerdir.
Vercher (2006), minimize edilen risk çerçevesinde elde edilen getirinin, risksiz
bir varlığın elde ettiği getiriden daha az olmadığı bir portföy oluĢturmak için bir çalıĢma
yürütmüĢtür.
Huang (2007), bulanık portföy seçiminde etkili olan risk için yeni bir tanımlama
geliĢtirmiĢtir. Yine aynı yıl bir baĢka makalesinde, portföy optimizasyonu için ortalamayarı varyans metodlarını kullanmıĢtır.
Hasuike ve ark. (2009), rastgele bulanık değiĢkenler gibi belirsiz olan beklenen
getiriler ile olasılık içeren, geleceğe yönelik beklenen getirileri içeren birkaç portföy
seçim problemini ele almıĢlardır.
Wu ve Liu (2010), portföy optimizasyonu problemi için bulanık beklentiyayılma (E-S) modeli geliĢtirmiĢlerdir. Yayılma terimi, Lebesgue-Stieltjes (L-S)
5
integralinde tanımlanmaktadır. Bu integralin hesaplamaları genellikle, sık sık kullanılan
trapez ve üçgen değiĢkenler için yaklaĢım Ģemasına ve bilgisayar yazılımına bağlıdır.
Yayılma terimi, bulanık parametreler yönünden ikinci dereceden fonksiyonlar olarak
temsil edilmektedir. Bu yeni temsiller, parametrik programlama problemine karĢılık
gelen E-S modeline dönüĢtürmeyi kolaylaĢtırmaktadır. Sonuç olarak, bulanık
parametreler göz önüne alındığında, E-S modeli genel amaçlı yazılım veya geleneksel
optimizasyon algoritmaları ile çözülebilecek bir karesel programlama problemi halini
almaktadır.
Sadjadi ve ark. (2011), farklı zaman döngülerindeki yatırımın miktarını
belirleyen bulanık doğrusal programlama yöntemini ele almıĢlardır. Getiri oranları ve
borçlanma/borç verme oranları dalgalı olarak ifade edilmekten ziyade üçgensel bulanık
sayılar olarak ifade edilmiĢtir. Bulanık küme teorisi kullanılarak, yatırımcıların elindeki
nakit miktarı ve karları için bir model geliĢtirilmiĢtir.
iii. Fiyat/Kazanç oranı ile ilgili kaynak araĢtırması;
Basu (1977), hisse senedine ait yatırım performansının F/K oranı ile iliĢkisini
incelediği çalıĢmasında Eylül 1956 - Ağustos 1971 dönemini ele almıĢtır. New York
Borsası‟nda alım satım iĢlemi yapılan 1400 sanayi firmasının hisselerini analizinde
kullanmıĢtır. Ele alınan dönem süresince, düĢük F/K oranına sahip portföylerin, yüksek
F/K oranına sahip menkul kıymetlere oranla daha yüksek getiri elde ettiklerini
belirtmiĢtir.
Kane ve ark. (1996) çalıĢmalarında, menkul kıymetler borsasındaki volatilitenin,
piyasa F/K oranı üzerindeki etkisini incelemiĢlerdir. Sermaye piyasasındaki volatilite
artıĢının piyasa F/K oranını ve hisse senedi fiyatını düĢürdüğü sonucuna varmıĢlardır.
Ayrıca sermaye piyasasındaki volatiliteyi bilmek suretiyle hisse senedi fiyatlarının
düĢeceğini tahmin etmenin, söz konusu piyasanın etkinliği ile çeliĢmediğini
vurgulamıĢladır. Çünkü piyasadaki volatilite artıĢının yol açtığı algılanan riskteki
yükseliĢ, yatırımcıların hisse senedi yatırımları için talep ettikleri risk primlerini,
dolayısıyla da iskonto oranlarını arttıracağını belirlemiĢlerdir. Ġskonto oranındaki artıĢın
ise hisse senedi fiyatlarını düĢüreceği sonucuna varmıĢlardır.
Aydoğan ve Güney (1996) çalıĢmalarında, ortalama F/K oranı ile temettü
veriminin ĠMKB‟ nda hisse senedi getirilerini tahmin edebildiğini incelemiĢlerdir. Elde
edilen sonuçlar ana hatlarıyla yatırımcılara olumlu sinyaller vermektedir. Hem F/K
6
oranı hem de temettü verimi 3 ile 12 ay sonrası hisse senedi getirilerinin tahmininde
önemli birer araç olarak ortaya çıkmaktadır.
Shen (2000) çalıĢmasında, ABD hisse senedi piyasasında yüksek F/K oranına
rağmen hem kısa hem de uzun dönemde hisse senedi fiyatlarında yükselmenin devam
edebileceğini söylemiĢtir. F/K oranlarının yüksek olduğu dönemleri izleyen dönemlerde
hisse fiyatının uzun dönemde artıĢ hızının yavaĢ, kısa dönemde hisse senedi piyasası
performansının güçsüz olduğunu ve F/K oranlarına rağmen hisse senedi fiyatlarının
artmaya devam edeceğini ileri sürmüĢtür. Yüksek F/K oranına rağmen hisse senedi
fiyatının artmasının üç temel nedeni olduğunu belirtmiĢtir. Bunlar;
- Ekonomide beklenen istikrarlı GSYĠH büyümesine bağlı olarak Ģirket
kazançlarının eskisinden daha hızlı büyümesinin beklenmesi,
- Hisse senetlerinin, yatırımcıların gözünde eskisine göre daha az riskli olması
nedeniyle hisse senedi fiyatlarını yükseltici etki yapacak Ģekilde daha fazla talep
etmeleri,
- Hisse senetlerine yatırım yapmak için yatırımcıların katlandığı iĢlem
maliyetinin düĢerek hisse senedi talebini arttırmasıdır.
Trevino ve Robertson (2002), F/K oranının hisse senetlerinin getirilerinin
geleceği ile yüksek derecede bağlantılı olduğunu ileri sürmüĢlerdir. ÇalıĢmalarında S&P
500 endeksi verilerini kullanarak F/K oranları ile 1, 2, 5, 8 ve 10 yıl sonraki getiriler
arasındaki iliĢkiyi incelemiĢlerdir. Nakit devir hızı oranını Ģirket baĢarısının ölçümünde
tamamıyla objektif bir ölçü olarak kabul etmesine rağmen, F/K oranının güvenli yatırım
yapmada subjektif kalabileceğini ileri sürmüĢlerdir. ÇalıĢmanın sonucunda F/K oranları
ile üç yıldan daha kısa dönemlerde ortalama getirileri arasında düĢük korelasyon olduğu
ortaya çıkarken, beĢ yıldan uzun dönemlerde getirileri arasında yüksek korelasyon
olduğu ortaya çıkmıĢtır. Diğer bir deyiĢle F/K oranlarının yüksek olduğu dönemleri
izleyen uzun dönem getiri oranları düĢükken, oranların düĢük olduğu dönemleri izleyen
uzun dönem getiri oranlarının yüksek olduğunu gözlemlemiĢlerdir. Trevino ve
Robertson‟a göre yüksek F/K oranı yatırımcıya Ģirket hakkında iyi bir fikir vermektedir.
Harney ve Tower‟a (2003) göre, hisse fiyatları kazanç Ģeklini belirten karı
yönetmek için firma yeteneğiyle temel bir iliĢkiyi gösterebilir. F/K oranının büyüklüğü
Ģirket karının değiĢkenlerini göstermektedir. Yeterince düĢük F/K oranının, hisse
pazarının düĢük değerini kapsamlı bir Ģekilde açıkladığını ileri sürmüĢlerdir. Aksine
yeterince yüksek F/K oranı, karı yönetmek için iĢletmenin yeterliliği olan yatırımcının
yüksek değerini göstermektedir.
7
Horasan (2009), temel analiz tekniğinin bir unsuru olan F/K oranının firmaların
getiri ve kapanıĢ fiyatları üzerindeki etkilerini tespit etmek için bir çalıĢma yapmıĢtır.
ÇalıĢma sonucunda, F/K oranı ve kapanıĢ fiyatı arasında anlamlı ve pozitif yönde bir
iliĢki gözlenirken, F/K oranı ve getiri arasında anlamlı fakat negatif yönde bir etki
gözlenmiĢtir.
Théoret ve Racicot (2010), Taylor (1986,1994) ve Nelson (1990) tarafından
geliĢtirilen stokastik modeller kullanılarak Kalman filtresi yardımı ile mali piyasaki
önemli değiĢkenlerin stokastik hareketliliğini tahmin etmek için GARCH modelini
kullanmıĢlardır. Bu modeldeki GARCH(1,1) değeri F/K oranı yardımıyla S&P500
borsasındaki hisse senetlerine uygulanarak bulunmuĢtur.
iv. ĠĢlem hacmi-getiri iliĢkisi ile ilgili kaynak araĢtırması;
Brailsford‟ un (1994) çalıĢmasında, fiyat değiĢimlerinin yönüne bakılmaksızın,
toplam pazar ve bireysel hisse senetleri için günlük iĢlem hacminin üç farklı ölçümü
için anlamlı sonuçlar ortaya çıkmıĢtır. Negatif getirilerin eğiminin, pozitif getirilerin
eğiminden daha dik olduğu hacim-fiyat değiĢimi hipotezini ispatlayan sonuçlara
ulaĢılmıĢtır. Bu çalıĢma, hacim-fiyat arasındaki iliĢkinin asimetrik olduğunu
destekleyen bir çalıĢma niteliğindedir. ÇalıĢmada GenelleĢtirilmiĢ Otoregresif KoĢullu
DeğiĢen Varyans (GARCH) modeli kullanılmıĢtır.
BaĢçı ve ark. (1996), Ocak 1998-Mart 1999 tarihleri arasında ĠMKB‟ de, 29
hisse senedi için haftalık fiyat ve iĢlem hacmi verileriyle çalıĢmıĢlardır. Fiyat ve iĢlem
hacmi değiĢkenleri arasında bir koentegre (ortak bütünleĢme) iliĢki olduğunu
bulmuĢlardır.
Lee ve Rui (2002), üç büyük hisse senedi piyasasında (New York, Tokyo,
Londra) çalıĢma yapmıĢlardır. New York ve Tokyo piyasalarında, nedensellik etkisinin
hisse senedi getirilerinden iĢlem hacmine doğru olduğu, iĢlem hacmi ile getiri
volatilitesi arasındaki feedback iliĢkisinin ise her üç piyasada geçerli olduğu sonucuna
varmıĢlardır.
Koulakiotis ve ark. (2006), GARCH ve EGARCH-M tekniklerini kullanarak;
Avustralya, Kanada, Fransa, Japonya, ABD, Almanya ve Ġtalya‟ yı kapsayan yedi ülke
için haftalık olarak hisse senedi getirileri, beklenen getiri ile hisse senedi piyasası
volatilitesinin stokastik bir davranıĢ sergilediğini ampirik bir bulgu ile ispatlamıĢlardır.
Kamath (2008), IPSA (ġili Santiago Borsası)‟ daki günlük, iĢlem hacmi ve
getiriler arasındaki ekonomik iliĢkiler için bir incelemede bulunmuĢtur. Ocak 2003-
8
Kasım 2006 dönemlerini kapsayan 950‟den fazla getiri-hacim çifti veri olarak
kullanılmıĢtır. 46 aylık bir periyot boyunca % 240 getiri elde edilmiĢtir. Bu çalıĢma
göstermiĢtir ki, IPSA‟ nın yükseliĢi artan iĢlem hacme eĢlik etmiĢtir. Aynı Ģekilde
IPSA‟ nın düĢüĢü iĢlem hacminin düĢüĢü ile doğru orantılı olmuĢtur. Hacim ile
getirilerin büyüklükleri arasında eĢ zamanlı iliĢki olduğu bulunmuĢtur. Bu iliĢki anlamlı
ve pozitiftir. Dolayısıyla iĢlem hacmi değiĢimlerinin, endeks hareketleri boyunca
meydana gelen getiriler için yardımcı bir araç olduğu görülmektedir.
Javid ve Mubarik (2009), Pakistan hisse senedi piyasası için yürüttükleri
çalıĢmalarında üç imalat sektöründen toplam 70 firmanın Temmuz 1998 - Ekim 2008
dönemindeki günlük verilerini kullanarak iĢlem hacmi, hisse senedi getirisi ve volatilite
arasındaki etkileĢimi incelemiĢlerdir. Bulgular, önceki gün gerçekleĢen iĢlem hacminin
Ģimdiki hisse senedi getirisi üzerinde önemli bir etkiye sahip olduğunu göstermektedir.
Granger nedensellik testi piyasa getirisi ile iĢlem hacmi arasında çift yönlü bir
nedensellik iliĢkisinin varlığını göstermektedir.
9
3. MATERYAL VE METOT
3.1. Materyal
Bu çalıĢmada,
ĠMKB 30 endeksi içerisinde yer alan ve Ocak 2007-Aralık 2009 tarihleri
arasında iĢlem gören 30 hisse senedine ait;
-
Getiri
-
Risk
-
Fiyat/Kazanç oranı (F/K)
-
Toplama-dağıtım endeksi (ADI)
Vadeli iĢlem ve Opsiyon Borsası‟nda ĠMKB 30 endeks sözleĢmesi opsiyon
primi kullanılarak,
LINDO 6.1 paket programı yardımıyla optimal portföy oluĢturulmaya
çalıĢılacaktır.
3.2. Metot
Bu çalıĢmada hisse senedi yatırımcıları için optimal portföy oluĢturulmaya
çalıĢılmıĢtır. Bu kapsamda Konno-Yamazaki DP modeline, bulanık doğrusal
programlama yaklaĢımının uygulandığı Werners‟ ın modeli temel alınmıĢtır. Mevcut
modele, hisse senetleri piyasalarındaki temel analiz ve teknik analiz yöntemlerinde
kullanılan kısıtlar eklenmiĢ ve bu doğrultuda yeni bir model oluĢturulmuĢtur.
Teknik analiz yöntemlerinden seçilen Toplama-dağıtım endeksi kısıtı, iĢlem
hacmi ile getiriler arasındaki pozitif iliĢkiden dolayı oluĢturulabilecek optimal portföy
için önemli bir kriterdir.
Temel analiz yöntemlerinden biri olan Fiyat/Kazanç oranı ise, Ģirketlerin
bilançoları incelenerek, mevcut durumları ve sektördeki gücü hakkında önemli ipuçları
vermektedir.
10
Önerilen modelin çözümüyle, sahip olunan varlıkların toplam getirilerini ve risk
faktörlerini göz önüne alarak, temel analiz ve teknik analiz yöntemleri yardımıyla,
minimum risk ve maksimum karı sağlayacak hisse senetleri seçilecektir. Bu aĢamadan
sonra Vadeli ĠĢlem ve Opsiyon Borsası‟ nda iĢlem gören ĠMKB 30 endeks sözleĢmesi
satın alınarak, opsiyonlu alım durumunda riskin ve karın ne Ģekilde değiĢeceği somut
bir örnekle incelenecektir.
3.3. Portföy ve Portföy Yönetimi
Portföy yönetimi, değiĢkenleri çok fazla olan ve piyasadaki güncel haberler ile
yatırımcının yönüne müdahale etmesini gerekli kılan, bu nedenle sürekliliği olan bir
yapıya sahiptir. Portföy yönetimi hakkında literatürde oldukça fazla çalıĢma
bulunmaktadır. Bu kısımda, portföy yönetimi ile ilgili tanımlar verilmiĢ, daha sonra da
portföy yönetiminin süreç akıĢı incelenmiĢtir.
3.3.1. Yatırım kavramı
Yatırım, maddi veya manevi (topluluk içinde prestij kazanma veya kendini
herhangi bir Ģirketin ortağı hissetme) çıkar, kar, kazanç sağlamak için önceden yapılan
harcama olarak tanımlanabilir. Yatırım bir kerede yapılabileceği gibi çeĢitli zamanlara
da yayılabilir. Yatırım, sahip olunan paranın değerini kaybetmesi tehlikesinden
korunma veya ödünç para ile yatırım yaptıktan sonra borcu faizi ile birlikte geri ödeyip
kar etme gibi çeĢitli amaçlarla yapılabilir (AkbaĢ, 1999).
3.3.2. Portföy tanımı
Portföy kelime anlamı olarak „cüzdan‟ demektir. Menkul kıymetler açısından
portföy, menkul kıymetlerden oluĢan bir topluluğu ifade etmektedir. Portföy, belirli
11
amaçları gerçekleĢtirmek isteyen yatırımcıların, sahip olduğu, birbirleriyle iliĢkisi olan
ve kendine öz ölçülebilir nitelikleri olan yeni bir varlıktır (DemirtaĢ ve Güngör, 2004).
Diğer bir deyiĢle, belirli bir kiĢi veya grup tarafından elde tutulan, ağırlıklı
olarak hisse senedi, tahviller gibi menkul kıymetten oluĢan bileĢkeye portföy adı verilir
(BeĢer, 2005).
3.3.3. Portföy yönetimi
Herhangi bir portföyün oluĢturulması aĢamasında yapılan iĢlemler bütünü
portföy yönetimi Ģeklinde ifade edilmektedir (Bozdağ ve ark., 2005).
Portföy yönetiminde amaç, karar vericinin risk ve getiriye karĢı gösterdiği tutum
çerçevesinde portföy içine hangi varlıkların hangi oranlarda gireceğine ve zamanla
değiĢen ekonomik koĢullara bağlı olarak hangi varlıkların portföyden çıkarılacağına
karar vermektir. Tüm karmaĢık problemlerde olduğu gibi portföy yönetiminde de
kararların verilmesi zordur ve uzun bir süreç gerektirir. Bunun nedeni, yatırımcının
kriterlerine uygun portföylerin oluĢturulmasında çok fazla sayıda ve karmaĢık yapıda
verileri kullanarak, istenilen özelliklere sahip portföylerin seçiminin zorluğudur
(Sezgin, 2008).
ÇeĢitlendirme prensibi, birden fazla menkul kıymete yatırım yaparak riskin
dağıtılmasını amaçlayan portföy yönetimi görüĢünde, yatırım çeĢitlendirildiği oranda
riskin de azalmasına dayanmaktadır. Portföy seçiminde, birbirleriyle iliĢkisiz
sektörlerden menkul kıymetler seçilerek etkili bir çeĢitlendirme ile risk azaltılabilir.
Gelecekle ilgili tüm kararlarda, kararın istenilen sonucu vermemesi tehlikesi vardır. Bir
finansal varlık yatırımcısının, yapacağı yatırımdan beklediği bir getiri vardır. Fakat
beklenen getirinin sağlanıp sağlanamayacağını yatırımı yapmadan bilmek imkânsızdır.
Yatırımcı, yapacağı her yatırımın taĢıdığı bu riske karĢı, kendisini kısmen veya
tamamen korumaya çalıĢır. Bu koruma yatırım araçları arasında herhangi bir getiri
seviyesinde en az risk taĢıyanı seçme Ģeklinde veya herhangi bir risk seviyesinde
yatırımının daha büyük getiri sağlamasını talep etme Ģeklinde olabilir. Gerek daha az
risk taĢıyan yatırım araçlarını seçmek, gerekse yüksek risk taĢıyan yatırımdan daha
yüksek getiri talep edebilmek için riskin büyüklüğünü ölçmek gerekir (Markowitz,
1952).
12
3.3.4. Portföy yönetimi süreci
Bir portföy yöneticisinin öngörülen risk sınıfında ortalama üzerinde getiri
sağlamak ve çeĢitlendirme ile sistematik olmayan bütün riskleri elimine etmek gibi iki
ana amacı olmalıdır. Bu iki amacı gerçekleĢtirmek için portföyün belirli bir süreç içinde
oluĢturulması gerekir. Portföy yönetimi sistemi dinamik bir süreç olup, beĢ aĢamadan
oluĢmaktadır (Sevil, 2001).
Bunlar;
-
Portföy Planlaması
-
Yatırım Analizi
-
Portföy Seçimi
-
Portföy Değerlendirmesi
-
Portföy Revizyonu‟ dur.
Bu aĢamaların birbirleri ile etkileĢimleri ġekil 3.1‟ de gösterilmiĢtir.
1-PORTFÖY PLANLAMASI
2-YATIRIM ANALĠZĠ
Yatırımcının Durumu
Yöneticinin Durumu
Yatırım Ölçütleri
Ekonomi Analizi
Sektör Analizi
Ġlk seçim
Tahmin Analizi
5-PORTFÖY REVĠZYONU
Genel Kompozisyon Kararı
Menkul Kıymet Seçimleri
Zaman Kararları
4-PORTFÖY
DEĞERLENDĠRMESĠ
Performans Ölçüleri
Performans KarĢılaĢtırmaları
3-PORTFÖY SEÇĠMĠ
Genel Kompozisyon Kararı
Menkul Kıymet Seçimleri
ġekil 3.1. Portföy yönetim süreci (AslantaĢ, 2008)
13
Portföy planlaması aĢağıdaki konuları kapsamaktadır:
-
Yatırımcının durumunun incelenmesi; yatırım süresinin açıklanması,
yatırımcının isteklerinin ve amaçlarının belirtilmesi, yatırım süresince
meydana gelecek fon hareketlerinin tahmini gerekmektedir. Yatırımcıyla
ilgili tüm bu bilgiler, sağlıklı bir portföy oluĢturulmasına yardımcı olacaktır.
-
Yatırım uzmanının veya portföy yöneticisinin durumunun saptanması;
yatırımcının kendisinin oluĢturduğu portföyden sağlayabileceği sonuçlardan
daha iyi sonuçlar alması veya geçerliliği kanıtlanmıĢ tesadüfi yatırım
yöntemleri ile sağlanabilecek sonuçlardan daha iyi sonuçlar alması gibi
faktörlerin incelenmesi gerekmektedir.
-
Yatırımcı adına faaliyette bulunan portföy yöneticisine yol gösterecek
yatırım ölçütlerinin saptanması; portföy planlamasının son aĢamasını
oluĢturmaktadır. Portföy yöneticisi, yatırım ölçütünü hem yatırımcının
hedeflerine, hem de kendi beklentilerine cevap verecek Ģekilde belirlemelidir
(Ceylan ve Korkmaz, 1998).
Yatırım analizi ise portföye alınacak menkul kıymetlerin niteliklerinin
incelenmesi,
ölçülmesi,
belirli
bir
süre
içinde
değiĢik
menkul
kıymetlerin
performanslarının ne olabileceğinin nicel olarak tahmin edilmesidir. Bu analizde önemli
olan, sadece yatırım yapılabilecek finansal varlıkların geçmiĢ performanslarının
incelenmesi ve değerlendirilmesi değildir. Ayrıca, çeĢitli bilgilerden yararlanılarak,
ileriye dönük açık ve matematiksel tahminlerin yapılması gerekir. Bu tür
hesaplamalarla, yatırım için uluslar arası veya ulusal ekonomik Ģartların uygun olup
olmadığı ortaya konulabilir. Ekonomik durum yatırım için elveriĢli ise, daha sonra,
hangi endüstrilerin geleceğinin daha iyi olacağına yönelik analizler yapılmalıdır. Daha
sonraki aĢamada ise belirlenen endüstride hangi iĢletmelerin menkul kıymetlerine
yatırım yapılacağının tespit edilmesi gerekir. Yatırım analizi aĢamalarını,
-
Ekonomik analiz
-
Sektör analizi
-
Menkul kıymetler arasından ilk seçim
-
Tahmin analizi
Ģeklinde sıralamak mümkündür (Ceylan ve Korkmaz, 1998).
Portföy seçimi aĢamasında, ilk önce her yatırım grubuna yapılacak yatırım tutarı
belirlenir. Daha sonra bu grup içinde farklı menkul kıymetlere yapılacak yatırım
tutarının belirlenmesi gerekir. Bu safhada yatırım uzmanı, yatırımcı adına ilk teĢebbüste
14
bulunur. Portföy seçiminde portföyün hangi varlıklardan oluĢacağı belirlenmektedir.
Daha sonra seçilen menkul kıymetlerden her birine ne kadar yatırım yapılacağı
belirlenir (Bekçi, 2001). Çünkü yatırım analizi, ekonomi analizi, sektör analizi, ilk
ayırım, tahmin analiz ve genel kompozisyon kararları bu seçime yönelik ön çalıĢmaları
oluĢturmaktadır (Ceylan ve Korkmaz, 1998).
Portföy yönetimi sürecindeki dördüncü aĢama, portföy değerlendirmesidir.
Sistemin dinamik özelliğinden dolayı, oluĢturulan portföyün belirli zaman aralıklarında
değerlendirilmesi gerekir. Bu aĢamada, zaman içerisinde portföyün verimi ve değerinde
olan değiĢiklikler incelenir. Sonuçlar, yatırım süresinin baĢında saptanan yatırımcının
amaçları ve yatırım ölçütleri ile değerlendirilir (AslantaĢ, 2008).
Portföy yönetiminde son aĢama portföy revizyonudur. Portföy revizyonu genel
ekonomi, endüstri kolu ve menkul kıymetlerle ilgili analizlerin sürekli olarak yapılması
faaliyetini kapsar. Portföy revizyonunda menkul kıymet seçimi ve yatırım zamanlaması
kararları önem kazanmaktadır. Portföy revizyonu yapılırken, menkul kıymetlerin alım
ve satımının gerekli olup olmadığı, hangi menkul kıymetlerde hangi oranda değiĢiklik
yapılması gerektiği, yatırım için yapılacak iĢlem tutarının ne olması gerektiği ve yatırım
iĢleminin ne zaman yapılacağı gibi sorulara cevap aranır (Berk, 2000).
3.3.5. Portföy çeĢitleri
DeğiĢik menkul kıymetlerden veya yatırım araçlarından, çok sayıda portföy
oluĢturulabilir. Ancak, olaya hisse senedi ve tahvil gibi geleneksel menkul kıymetler
açısından bakıldığında;
-
Bütünü tahvillerden oluĢan
-
Belirli oranda hisse senedi ve tahvili birlikte içeren
-
Bütünü hisse senedinden seçilmiĢ
üç farklı portföyden söz edilebilir. Oysa ki, bir portföy hisse senedi ve tahvil gibi temel
menkul kıymetler dıĢındaki yatırım araçlarıyla da belirlenebilir. Yatırım süresi boyunca
hangi tür varlıkların daha verimli olacağı çeĢitli istatistik tekniklerle değerlendirilerek
portföy seçimi gerçekleĢir. Hisse senedi ve tahvil dıĢındaki yatırım araçlarını;
Varlığa dayalı menkul kıymet
Finansman bonoları
15
Hazine bonosu
Gelir ortaklığı senetleri
Banka bonoları veya banka garantili bonolar
Metrekare konut sertifikaları
Mevduat ve mevduat sertifikaları
Repo
Döviz ve döviz tevdiat hesapları
Altın
olarak sıralamak mümkündür. Yatırımcıların portföylerinden beklentileri farklı
derecelerde olabileceği için yapılacak bir portföy çeĢitlendirme, yatırımcı özelliklerine
göre değiĢiklik gösterecektir (Sezgin, 2008).
3.4. Yatırımlarla Ġlgili Riskler ve Yatırımın Getirisi
Yatırımcılar ellerindeki varlıkları korumak, gelirlerini arttırmak ya da riski
dağıtmak koĢuluyla, gelirlerini yaĢamları boyunca en üst düzeyde tutmaya çalıĢırlar. Bu
nedenle risk ve getiri arasında bir kıyaslama yapmak zorundadırlar. Yatırımcıları, risk
parametresi altında üç ayrı sınıfa yerleĢtirmek mümkündür. Bunlar;
Riskten kaçan yatırımcılar: Adından da anlaĢılacağı üzere riski
i.
sevmezler ve riskten kaçarlar. Bu tür yatırımcılar, beta katsayısı düĢük olan
hisse senetlerini tercih ederler. Bundan dolayı bu tür yatırımcılar, yapacakları
yatırımlarda tercih söz konusu ise aynı getiri altında riski daha az olanı tercih
ederler.
ii.
Riske karşı kayıtsız yatırımcılar: Riske karĢı kayıtsız kalan bu tür
yatırımcılar, riskle ilgilenmezler. Bu tür yatırımcılar için hangi yatırımın
seçileceği çok önemli değildir.
iii.
Riski seven yatırımcılar: Bu tür yatırımcılar, yüksek getirinin yüksek risk
düzeyi ile elde edileceğini varsayarlar. Getiri ne kadar yüksek olursa, risk de o
kadar yüksek olacaktır. Yatırımcılar daha yüksek getiriyi tercih ederse, aynı
oranda daha yüksek bir riski de kabul ediyor demektir (Bekçi, 2001).
16
3.4.1. Risk nedir?
Yatırımcıların, hisse seçimlerinde daha bilinçli olabilmeleri için, nelere
bakmaları gerektiği ve hissenin baĢarısını nasıl değerlendirebilecekleri konusu
önemlidir. Öncelikle, risk ve getiri iliĢkisi, bir hisse senedinin baĢarısını
değerlendirirken yatırımcılar tarafından dikkate alınması gereken en önemli unsurdur.
Hisse senedi getirisini ölçmek kolaydır; ancak riskin değerlendirilmesi konusundan
önce "risk nedir?" sorusuna açıklık getirilmesi gerekir. Sermaye piyasalarında risk, çok
genel olarak, "beklenen getirinin gerçekleĢen getiriden sapma olasılığı" olarak
tanımlanabilir. Bir baĢka anlatımla, herhangi bir yatırım aracının getirisi, beklenen
getiriden ne kadar büyük farklılık veya sapma gösteriyorsa, söz konusu yatırım aracının
riski, o kadar yüksek demektir (Turanlı ve ark., 2002).
3.4.2. Risk çeĢitleri
Portföy kuramında yatırımcının riski kontrol altına alabilme veya sınırlayabilme
olanağının olup olmamasına göre, toplam risk; sistematik risk ve sistematik olmayan
risk olarak iki ana gruba ayrılmaktadır.
i. Sistematik risk: Piyasada iĢlem gören tüm menkul kıymetlerin fiyatlarını aynı
anda etkileyen faktörlerin neden olduğu risktir. Beklenen getirinin sistematik
değiĢkenliği, hemen hemen tüm menkul kıymetler için değiĢen derecelerde mevcuttur.
Çünkü menkul kıymetlerin fiyatlarının çoğu sistematik bir Ģekilde aynı yönde hareket
eder. Yatırımcılar açısından sistematik riskin kontrol olanağı yoktur. Bu nedenle portföy
yönetiminde tek belirsizlik kaynağının sistematik risk olduğu ifade edilebilir. (Ceylan
ve Korkmaz, 1998).
Sistematik riskin baĢlıca kaynakları Ģunlardır;
-
Piyasa riski
-
Faiz oranı riski
-
Enflasyon riski
-
Politik risk
Sistematik risk, portföyün çeĢitlendirilmesi ile giderilemeyen risk olarak da
tanımlanabilir. Genelde, temel endüstriyel maddeler üreten iĢletmelerde ve dolayısıyla
17
söz konusu iĢletmelerin hisse senetleri üzerinde, sistematik riskin daha yüksek olduğu
gözlenmiĢtir (Akgüç, 1998).
ii. Sistematik olmayan risk: Bir Ģirket veya sektöre özgü olan risktir. ĠĢçi grevi,
yönetim hataları, keĢifler, reklâm kampanyaları, tüketici tercihlerindeki değiĢmeler,
Ģirket gelirinde sistematik olmayan değiĢmelere yol açabilir. Sistematik olmayan
faktörler, diğer endüstriler ve genel olarak menkul kıymetler piyasasını etkileyen
faktörlerden bağımsızdır (Ceylan ve Korkmaz, 1998). Sistematik riskin kontrol edilmesi
imkânsızken, sistematik olmayan riskin kaynaklarında yapılan değiĢmelerle ve
yönlendirmelerle azaltılması veya yok edilmesi mümkündür. Çok iyi çeĢitlendirilmiĢ bir
portföyde sistematik olmayan risk, sistematik risk seviyesine kadar düĢürülebilir
(AslantaĢ, 2008).
Menkul kıymetler arası iliĢkiye dikkat edildiği taktirde portföyün sistematik
olmayan riski azaltılabilmekte hatta sıfırlanabilmektedir (Markowitz, 1952).
Sistematik olmayan riskin baĢlıca kaynakları Ģunlardır;
-
Finansal risk
-
ĠĢ ve endüstri riski
-
Yönetim riski
-
Likidite riski
Sistematik risk ve sistematik olmayan risk ġekil 3.2‟ de gösterilmiĢtir. ġekilde
görüldüğü gibi sistematik risk sıfıra indirilebilirken; sistematik olmayan risk,
sistematik risk kadar düĢürülebilir.
Risk
Sistematik
Olmayan Risk
Sistematik Risk
Portföydeki
Yatırım Aracı
Sayısı
ġekil 3.2. Sistematik ve sistematik olmayan risk (Turan, 2001)
18
3.4.3. Risk ve getiri hesapları
Portföy seçiminde dikkatle incelenmesi gereken iki önemli konu vardır. Bunlar;
risk ve getiridir. Yatırımcılar, ellerindeki varlıklarına yön verirken bu iki konuyu
mukayese etmek zorundadırlar.
3.4.3.1. Beklenen getiri
Menkul kıymetlere yatırım yapan yatırımcılar, menkul kıymetin türüne göre
kazanç beklemektedir. Söz konusu kazanç, faiz geliri, kar payı ve menkul kıymetlerin
fiyatındaki artıĢın neden olacağı değerlerdir. Menkul kıymetlerin getirisi, ekonominin,
endüstrinin ve iĢletmenin durumundaki değiĢmelerle yakından ilgilidir. Ayrıca,
yatırımlardan beklenen getiri oranları menkul kıymetin türüne göre de değiĢmektedir.
Örneğin, devlet tahvili ve özel sektör tahvillerinden beklenen getiriler farklıdır. Devlet
tahvilleri, riski en az menkul kıymet kabul edildiğinden, beklenen getiri risksiz faiz
oranı olarak kabul edilir. Bu getiriye risksiz faiz oranı denilmesinin nedeni, sağladığı
getirilerin kesin olmasındandır. Çünkü tahvilin anapara ve faiz ödemeleri devletin
garantisi altındadır. Yatırımcı, devlet var olduğu ve hazine iflas etmediği sürece
beklediği getiriyi elde edecektir (AslantaĢ, 2008).
Hisse senetlerine bakacak olursak, bir portföyün getiri oranı portföyde yer alan
menkul kıymetlerin getirilerinin ağırlıklı ortalamasına eĢittir. Her bir getiriye uygulanan
ağırlık, bu getirinin ait olduğu menkul kıymetin portföy içindeki oranıdır. n kadar
menkul kıymetten oluĢan bir portföyün beklenen getirisi, Ģu Ģekilde hesaplanır (Ceylan
ve Korkmaz, 1998):
n
E(R p )
x jE(R j )
j =1
Burada,
E(R p ) : Portföyün beklenen getirisi
E(R j ) : j. menkul kıymetin beklenen getirisi
xj
: j. menkul kıymetin portföy içindeki oranını göstermektedir.
(3.1)
19
3.4.3.2. Standart sapma ve varyans
Portföyün varyansı veya varyansın karekökü olan standart sapma portföyün
riskini ifade etmektedir. Bu ölçü, portföyün ortalama getirisinin beklenen getiriden ne
kadar saptığını göstermektedir. Bu ifade aynı zamanda portföyün toplam riskini
vermektedir. Standart sapmanın veya varyansın küçük olması yatırımcılar için istenen
bir durumdur.
Portföyün varyansı veya riski, büyük ölçüde portföyü oluĢturan menkul
kıymetlerin birbirleriyle olan iliĢkilerinden yani korelasyonundan kaynaklanmaktadır
(Bekçi, 2001).
Ġki farklı yatırım portföyü eĢit varyansa sahipse, bunların birleĢiminden oluĢan
yeni portföyün varyansı, her birinin varyansından daha küçük olmaktadır (Markowitz,
1952).
3.4.3.3. Kovaryans
Menkul kıymetlerin tek tek risklerini standart sapma veya varyansla ölçmek
mümkündür. Ancak, iki veya daha çok menkul kıymet yani bir portföy söz konusu
olduğunda risk, kovaryans ile ifade edilir (Markowitz, 1952). Kovaryans,
N
(R ij - E(R i )).(R kj - E(R k ))
COVR i ,R k
j =1
N -1
(3.2)
biçiminde, getirilerdeki sapmaların çarpımları toplamının (N-1) ile bölünmesiyle
hesaplanır. Beklenen getirilerin gerçekleĢme olasılıkları kullanılarak kovaryans
hesaplanmak istenilirse;
N
COVR i ,R k
Pij (R ij - E(R i )).(R kj - E(R k ))
j =1
eĢitliğinden yararlanılır.
(3.3)
20
Burada,
R i , R k : i ve k hisse senetlerinin Pi olasılığına bağlı getirilerini ifade etmektedir.
Kovaryans katsayısı pozitif ise; menkul kıymet getirileri arasında bir eĢyönlülük
olduğunu gösterir. Yani, menkul kıymetlerden birisinin getirisi, ortalama getiriden fazla
ise diğer menkul kıymetin getirisinin de ortalama getiriden fazla olacağı söylenebilir.
Kovaryans katsayısı negatif ise; menkul kıymet getirileri arasında ters yönlü bir
iliĢki vardır. Negatif katsayı ne kadar büyük ise, ters yönlü iliĢki o derece güçlüdür.
Kovaryans katsayısının sıfır veya sıfıra yakın bir değerde olması, menkul
kıymetler arasında doğrusal bir iliĢkinin bulunmadığını gösterir (Ceylan ve Korkmaz,
1998).
3.4.3.4. Korelasyon katsayısı
Portföye dahil edilecek menkul kıymetlerin getirileri arasındaki iliĢkinin yön ve
derecesinin belirlenmesinde kullanılan ölçütlerden biri de korelasyon katsayısıdır.
Bilindiği gibi korelasyon, iki değiĢkenin arasındaki iliĢkinin derecesinin tespitinde
kullanılır. Korelasyon katsayısı, iki değiĢkenin değiĢimlerinde ne dereceye kadar
uygunluk olduğunu belirler. Fakat hiçbir Ģekilde sebep-sonuç iliĢkisini ortaya koymaz
(Serper, 1986).
Hisse senetlerinin getirileri arasındaki iliĢkinin derecesini ölçmekte kullanılan
korelasyon katsayısı, kovaryansın, iki menkul kıymetin standart sapmalarının çarpımına
bölünmesiyle bulunur (Ceylan ve Korkmaz, 1998).
Korelasyon katsayısı,
Pi,k
COVRi , R k
σi .σ k
(3.4)
Ģeklinde ifade edilir. Korelasyon katsayısının (+1) veya yakın bir değer alması
değiĢkenler arasında aynı yönde bir iliĢki olduğu anlamına gelirken; (-1) veya yakın bir
değer alması ise ters yönde bir iliĢki olduğu anlamına gelir. Özellikle aynı endüstride
21
faaliyet gösteren iĢletmeler arasında ve birbirlerini tamamlayıcı durumda bulunan
sektörler için, pozitif tam korelasyondan söz etmek mümkündür (Ceylan ve Korkmaz,
1998).
3.4.3.5. Beta katsayısı
Sistematik olarak ve çeĢitlendirme ile ortadan kaldırılamayan finansal varlıkların
riski, hisse senedi yatırımcılarını ilgilendiren göstergelerden biri olan Beta katsayısı ile
temsil edilmektedir (AkbaĢ, 1999).
Yatırımcı finansal varlığa yatırım yaparken, standart sapma ile belirlediği toplam
risk yanında, hisse senedinin pazar içindeki konumunu bilmesinde yarar vardır. Hisse
senedinin riskinin pazara ait ortalama bir hisse senedinin riskine kıyasla ne durumda
olduğu ve pazarda ortaya çıkan değiĢmelerden ne ölçüde olumlu veya olumsuz
etkileneceği hakkındaki bilgiler yatırımcının karar vermesinde etkili olabilir. Örneğin,
pazar riskinde bir puanlık artıĢ veya azalıĢ, hisse senedinin riskinde nasıl bir değiĢiklik
yapacaktır. ĠĢte bir hisse senedinin pazarla birlikte hareket etme eğilimi, o hisse
senedinin “β” katsayısı ile belirlenebilir (AkbaĢ, 1999).
Riski çeĢitlendirilmiĢ bir optimal portföyün bulunması, tüm karar olanaklarının
analiz edilerek belirli bir kritere göre sıralanmasını gerektirir. Seçim, beklenen hedeflere
uygun olarak beklenen faydanın ya da getirinin maksimum kılınması ile gerçekleĢtirilir.
Karar alternatifinin gruplandırılması, öngörülen hedefler nedeniyle, portföyün beklenen
her öz sermaye kârlılığı için çeĢitli menkul kıymetlerin veri getiri oranları ile
varyansları ve kovaryanslarının minimum kılındığı bir portföyün yapısının bulunması
ile gerçekleĢir. Portföyün beklenen getirisi yatırımda kullanılan sermayenin bireysel
varlıkların ağırlıklı getiri paylarının toplamına eĢittir (Anonim, 2002). Beta katsayısı,
βj
Cov(j,m)
Var(m)
(3.5)
biçiminde gösterilir. Burada; j, hisse senedi ve pazar portföyü arasındaki kovaryansın
pazar portföyü varyansına oranı, β katsayısını veya yatırımcı tarafından istenen risk
primini vermektedir. Beta katsayısı, bir hisse senedinin getirisinin hisse senedi pazarının
22
bir bütün olarak getirisine paralel bir değiĢme gösterip göstermediğini ortaya
koymaktadır (Ceylan ve Korkmaz, 1998).
Eğer β >1 ise, portföyün getirisinde, piyasanın getirisindeki değiĢme ile aynı
yönde ve ondan daha büyük bir değiĢme olacaktır. Bu tür hisse senetlerine “atak” hisse
senetleri denir. Söz konusu hisse senetlerinin pazara karĢı duyarlılıkları fazladır. Pazar
portföyünün getirisinde %1 artıĢ olduğunda, atak hisse senedinin getirisindeki artıĢ
%1‟den daha fazla olur. BaĢka bir deyiĢle, borsada fiyat artıĢları olduğunda, atak hisse
senetlerinin fiyat artıĢı ortalama artıĢın üzerinde gerçekleĢir.
Eğer -1 < β < 1 ise, portföyün getirisinde, piyasanın getirisindeki değiĢmeden
daha küçük bir değiĢme olacaktır.
Eğer β < -1 ise, portföyün getirisinde, piyasanın getirisindeki değiĢme ile ters
yönde ve ondan daha büyük bir değiĢme olur. Beta katsayıları 1‟den küçük olan ve
“tutucu” diye adlandırılan hisse senetlerinin, pazara karĢı duyarlılıkları zayıftır. Pazar
portföyünün getirisindeki %1 artıĢ, tutucu hisse senedinin getirisinden daha düĢük bir
artıĢa neden olur. Yani borsada fiyatlar artarken, bu hisse senetlerindeki fiyat artıĢı
ortalama artıĢtan daha az olur (Ceylan ve Korkmaz, 1998).
Bir menkul kıymetin beta katsayısının 1‟den yüksek olması, menkul kıymetin
fiyatının piyasadan daha fazla yükseleceğini ya da düĢeceğini gösterir. Örneğin beta
katsayısı 1,25 olan bir menkul kıymetin fiyatının piyasadan %25 daha fazla yükseleceği
ya da düĢeceği beklenir. Piyasa %1,00 yükseliyorsa, menkul kıymetin fiyatının %1,25
yükselmesi, piyasa %1,00 düĢüyorsa, menkul kıymetin fiyatının da %1,25 düĢmesi
beklenir. Bir menkul kıymetin beta katsayısının 1‟den düĢük olması, menkul kıymetin
fiyatının piyasadan daha az yükseleceğini ya da düĢeceğini gösterir. Örneğin beta
katsayısı 0,80 olan bir menkul kıymetin fiyatının piyasadan %20 daha az yükseleceği ya
da düĢeceği beklenir. Piyasa %1,00 yükseliyorsa, menkul kıymetin fiyatının %0,80
yükselmesi, piyasa %1,00 düĢüyorsa, menkul kıymetin fiyatının da %0,80 düĢmesi
beklenir (Halıcı, 2008).
23
3.5. Fiyat/Kazanç Oranı
Yatırımcıların, fon birikimlerini uygun yatırım alanlarında değerlendirme kararı
zor bir süreçtir. Tasarrufların hisse senetlerine aktarılmak istenmesi durumunda,
piyasaların izlenmesi, elde edilen bilgilerin değerlendirilmesi ve çeĢitli yöntemler
kullanılarak en uygun hisse senetlerinin seçilmesi gerekir. Tüm bu değerlendirme
sürecindeki amaç, düĢük değerlenmiĢ veya getiri potansiyeline sahip hisse senetlerini
belirleyerek yatırım kararı vermektir. Hisse senedi seçiminde yatırımcılar kullandıkları
modellerle farklı bakıĢ açılarına uygun varlığın seçimini hedeflemektedirler (Horasan,
2009).
Finans uzmanları ya da yatırımcılar, firmaların sahip oldukları likidite, borç,
etkinlik ve kârlılık oranları dıĢında, firmanın piyasadaki performansını ölçmeye yönelik
piyasa temelli oranlardan da yararlanmaktadır. Özellikle sermaye piyasasının
geliĢmesiyle birlikte önem kazanan piyasa temelli oranlar, menkul kıymet
yatırımcılarına yol gösterici nitelikte bulunmaktadır. Oranların kullanılmasındaki temel
amaç, hisse senetlerinin gerçek piyasa değerlerine ulaĢmasında katettikleri yolun ve
zamanın belirlenmesi olmaktadır.
Hisse senetlerinin göreceli değerlemesinde kullanımı en yaygın olan oran, hisse
senedinin piyasa fiyatının hisse baĢına kâra bölünmesi ile bulunan Fiyat/Kazanç (F/K)
oranıdır. GeliĢmiĢ ve geliĢmekte olan piyasalarda sıkça kullanılan F/K oranı, piyasa
analistleri ve potansiyel yatırımcılar için firmanın 1 TL‟ lik vergi sonrası hisse baĢına
kârına karĢılık piyasadaki değerinin ne olması gerektiği konusunda önemli bir iĢarettir.
Bir baĢka ifadeyle bu oran, hisse senedi için ödenen bedelin hisse baĢına kazancın kaç
katı olduğunu açıklamaktadır (Öztürk, 2007).
F/K oranı, banka ve aracı kurumlardaki piyasa analistleri ve yatırımcılar
tarafından Ģirketlerin ve endüstri kollarının potansiyel kârlılıklarını karĢılaĢtırmak için
yaygın olarak kullanılmaktadır. Türkiye‟ de F/K oranı aracı kurumlar ve bankalar
tarafından en çok kullanılan değerleme yöntemidir (Öztürk, 2007).
F/K oranı, bir hissenin değerinin düĢük ya da yüksek olduğunu gösterir. Bu
oranın genel olarak düĢük çıkması tercih edilir. Bununla birlikte oranın düĢük veya
yüksek olduğu, aynı sektörde faaliyet gösteren diğer iĢletmelerin F/K oranı ile veya
sektörün ortalama F/K oranı ile karĢılaĢtırılması sonucunda anlaĢılır (Taner ve Akkaya,
2003).
24
Bu oran, Ģirketin ürettiği her bir birim net kâr baĢına piyasada biçilen değeri
ifade etmektedir. Oranın yüksekliği, hisse senedi fiyatının yüksek değerlendiğini ya da
yatırımcıların
Ģirkette,
gelecekte
yüksek
kâr
üretme
potansiyeli
gördüğünü
göstermektedir. Temel olarak ĠMKB de Fiyat/Kazanç oranı;
Fiyat/Kazanç
Toplam Piyasa Değeri
Net Kâr
(3.6)
formülüyle hesaplanmaktadır. Toplam piyasa değerinde, hesaplama tarihi itibariyle en
son kapanıĢ fiyatı ve toplam hisse sayısı dikkate alınmaktadır. Formüldeki net kâr üç
farklı yaklaĢımla bulunmakta ve bunlara göre üç farklı Fiyat/Kazanç oranı
hesaplanmaktadır (Anonim, 2008).
i.
Fiyat/Kazanç Oranı (TL1) = Toplam piyasa değeri / Son iki altıĢar aylık
bağımsız denetimden geçmiĢ dönemin net kârlar-zararlar toplamı
Bu yöntemde Ģirketlerin son 12 aylık net kâr/zarar rakamları, bağımsız
denetimden geçmiĢ altı aylık ve yıllık mali tablolarındaki net kâr/zarar rakamları
kullanılarak elde edilmektedir.
ii.
Fiyat/Kazanç Oranı (TL2) = Toplam piyasa değeri / Son dört üçer aylık
dönemin net kârlar-zararlar toplamı
Bu yöntemde Ģirketlerin son 12 aylık net kâr/zarar rakamları, üçer aylık
dönemler itibariyle gönderdikleri mali tablolarındaki net kâr/zarar rakamları
kullanılarak elde edilmektedir. Her yeni üçer aylık mali tablo açıklandığında, son dört
çeyrek kârları/zararları kaydırılarak son 12 aylık döneme isabet eden net kâr/zarar tutarı
hesaplanmaktadır.
iii.
Fiyat/Kazanç Oranı (ABD$) = ABD$ bazında Toplam piyasa değeri /
Son dört üçer aylık dönem ABD$ olarak net kârlar-zararlar toplamı
Bu yöntemde ise her üç aylık döneme isabet eden kâr/zarar, dönem sonu
kurundan ABD Dolarına çevrilmektedir. Her yeni üçer aylık mali tablo açıklandığında,
son dört çeyrek kârları/zararları kaydırılarak son 12 aylık döneme isabet eden ABD
Doları bazında net kâr/zarar tutarı hesaplanmaktadır. Piyasa değeri de oranın
25
hesaplanma tarihindeki kurdan ABD Dolarına çevrilmek suretiyle hesaplamada dikkate
alınmaktadır.
Fiyat/Kazanç oranı ĠMKB‟de bu üç yöntemle hesaplanmakta ve ilan
edilmektedir. Formüllerin paydası negatif veya çok küçük olduğunda, Fiyat/Kazanç
oranı anlamlı olmadığından hesaplanmamaktadır (Anonim, 2008).
F/K oranının zarar eden firmalara uygulanamaması bu oranın bir dezavantajını
oluĢturmaktadır (Öztürk, 2007).
DüĢük F/K oranına sahip hisse senetlerinin yatırım performanslarının F/K oranı
yüksek hisse senetlerine göre daha baĢarılı olduğunu ilk defa Nicholson (1960) ortaya
koymuĢtur (Karan, 2001).
DüĢük F/K oranlı hisseler yatırım için verimli bir sahadır. Hisseler son 52
haftalık en yükseklerinden %50‟ lik bir düĢüĢ gösterdikten sonra, Ģirketlerin para
kazanma yetenekleri göz önüne alınarak hangisinin ucuz kaldığını belirlemekte F/K
analizi kullanılabilir. DüĢük F/K oranlı hisselere yatırım yapmanın faydalarını birçok
inceleme göstermiĢtir. Son 12 ayın veya son mali yılın kârlarını baz alan bir F/K
oranının 12‟ den az olması teyit edici bir gösterge olabilir. Buna alternatif olarak, son
beĢ yıl içinde oluĢan en yüksek F/K oranının %40 altında iĢlem gören hisseler göz
önüne alınabilir. Hangi formül kullanılırsa kullanılsın, alımdan önce düĢük F/K eleğinin
uygulanmasının portföy için büyük faydaları olduğu göz ardı edilmemelidir (Gallea ve
Patalon, 1998).
Birçok yatırımcı kazançların piyasada nasıl oluĢtuğu ile ilgilenir. Bu kazançların
değerlendirildiğini gösteren F/K oranı,
F/K Oranı
Hisse Senedinin Piyasa Fiyatı
Hisse Başına Kazanç
Hisse Başına Kazanç HBK
Dağıtılabilir Net Kâr
Hisse Senedi Sayısı
(3.7)
(3.8)
biçiminde de gösterilmektedir. Burada paydada yer alan hisse baĢına kazanç, vergi
sonrası net kârda, imtiyazlı ve kurucu hisselere ödenen temettü ve yönetim kurulu
üyelerine ve çalıĢanlara ödenen temettü çıkarıldıktan sonra, kalan kârın ağırlıklı
ortalama hisse sayısına bölünmesiyle bulunmaktadır. Hisse senedi piyasa fiyatı, dönem
sonu piyasa fiyatıdır (BaĢtürk, 2004).
26
Hisse senetlerinin analizinde, bir hisse senedinin beklenen F/K oranının
hesaplanması yatırımcılar için gerekli kılınır. Beklenen F/K oranı veya diğer bir deyiĢle,
kazanç çarpanı; hisse baĢına kazanç tahminlerinin, hisse senedinin cari piyasa fiyatına
bölünmesidir (BaĢtürk, 2004).
Beklenen F/K
Hisse Başına Tahmin Edilen Kazanç
Cari Piyasa Fiyatı
(3.9)
formülü ile hesaplanmaktadır. Bu yöntemde genel olarak firmaların F/K oranları
beklenen F/K oranları ile veya piyasa ortalamaları ile karĢılaĢtırılmaktadır.
KarĢılaĢtırma sonuçları Ģu üç koĢuldan birini gündeme getirir (BaĢtürk, 2004):
i. Eğer gerçek F/K oranı beklenen F/K oranından büyükse, hisse senedi
değerinden yüksek fiyatlanmıĢtır, fiyatı düĢmeden satılmalıdır.
ii. Eğer gerçek F/K oranı beklenenden küçükse hisse senedi değerinden düĢük
fiyatlanmıĢtır, fiyatların yükselmesine sebep olan bir beklenti ile satın
alınabilir.
iii. Gerçek F/K oranı beklenen F/K oranına eĢitse, hisse senedi doğru
fiyatlanmıĢtır ve önemli bir fiyat değiĢikliklerinin olma olasılığı yoktur.
Bu prosedür hisse senetlerinde satma ya da satın almayla ilgili karar vermede
geniĢ çapta kullanılan bir yöntemdir. Pek çok sayıda menkul kıymet yöneticisi bu
prosedürü kullanır. Sonuçta yüksek fiyatlanmıĢ hisse senetlerinin fiyatları, F/K
oranlarının satıĢ baskısıyla, düĢük bir seviyede olabilecektir. DüĢük fiyatlanmıĢ hisse
senetlerinin hem fiyatları hem de F/K oranları artmaya baĢlayacak ve doğru fiyatlanmıĢ
hisse senetlerinin fiyatlarında, değiĢikliğe neden olacak tutarlı bir satın alma ya da
satma baskısı olmayacaktır. Piyasadaki baskıların hisse senedi fiyatlarını, gerçek
değerlere yakın fiyatlarda tutma eğiliminin olduğu, temel analistlerin ortak düĢüncesidir
(BaĢtürk, 2004).
Aynı Ģekilde hisse senetlerinin F/K oranları ile içinde bulunduğu sektörün F/K
oranları kıyaslandığında (BaĢtürk, 2004),
i.
Hisse senedinin F/K oranı, içinde bulunduğu sektörün F/K oranından
büyük ise hisse aĢırı fiyatlanmıĢtır ve elden çıkartılmalıdır.
ii.
Hisse senedinin F/K oranı, içinde bulunduğu sektörün F/K oranından
küçük ise hisse düĢük fiyatlanmıĢtır ve satın alınabilir.
27
3.6. ĠĢlem Hacmi ile Getiri ĠliĢkisi
ĠĢlem hacmi, borsada o gün gerçekleĢen alıĢ veriĢin, parasal olarak miktarı
(değeri) ya da sözleĢme adedi (lot) Ģeklinde ifade edilen rakamsal bir ifadesidir.
Aslında iĢlem hacmi hakkında tüm söylenecekleri Charles Dow yüz yılı aĢkın bir süre
önce tek bir cümleyle özetlemiĢ: “Hacim trendi teyit etmelidir”. ĠĢlem hacminin
seviyesi
fiyat
hareketinin
arkasındaki
desteği,
kabullenmiĢliği
ve
heyecanı
gösterir. Dolayısıyla hisse senedi piyasalarında, fiyatlar yükseldikçe iĢlem hacminin
artması, yatay piyasalarda
ve fiyatlar düĢtükçe de iĢlem hacminin azalması
beklenir. Durum böyle olduğu müddetçe, iĢlem hacmi trendi teyit eder. Ana trend
yukarıyken fiyatların aĢağı doğru düzeltme yapması süresince iĢlem hacminin azalması,
yukarı hareket için bir tehlike arz etmez. Çünkü azalan iĢlem hacmi düĢük maliyetli
uzun pozisyon tutanların kâr almak için acele etmediklerini gösterir. Ana trend
yukarıyken, aĢağı düzeltme esnasında iĢlem hacminin artması bu ana trendin artık sona
erdiğine iĢaret eder.
ĠĢlem hacminin fiyat hareketini teyit etmediği durumları
belirlemenin en iyi yolu, fiyat ile iĢlem hacmi arasındaki uyuĢmazlığa bakmaktır.
Fiyatlar yükselirken iĢlem hacminin bu yükseliĢe eĢlik etmemesi veya azalması fiyat
yükseliĢinin fazla devam etmeyeceğine iĢaret eder. Fiyatların bir konsolidasyon
(sıkıĢma) alanından belli bir yöne çıkıĢının müjdecisi olan kırılma anında ise iĢlem
hacminin genellikle dramatik bir Ģekilde artması beklenir. Bu artıĢ, o yöne doğru
baĢlayan yeni bir trendin habercisidir (PerĢembe, 2006).
ĠĢlem hacmi, bir piyasadaki yatırımcıların piyasaya gelen yeni haberlere
kümülatif tepkisini yansıtmaktadır. Aynı zamanda iĢlem hacmi; piyasaya etki eden,
gözlenemeyen bilgi akıĢını ölçen önemli bir göstergedir (Kıran, 2010).
ĠĢlem hacmi, hisse senedi fiyatları gibi sık dalgalanan ve genellikle aynı piyasa
riskleriyle hareket eden bir değiĢkendir ve iĢlem hacmi ile hisse senedi fiyatları, hisse
senedi pazarı performansına ait önemli iki göstergedir (Rashid, 2007).
Yüksek iĢlem hacmi, yatırımcılar için olumlu bir kriterdir ve pratikte iĢlem
hacminden yola çıkarak getirileri tahmin etme olasılığı yatırımcılara cazip gelmektedir.
Bu konuda eski iki Wall Street özdeyiĢi yatırımcılara ve araĢtırmacılara ilhan kaynağı
olmaktadır. i. ĠĢlem hacmi fiyatları yukarı iter. ii. Boğa piyasalarında iĢlem hacmi ile
fiyatlar arasında güçlü bir iliĢki vardır, ayı piyasalarında ise bu iliĢki zayıftır (Umutlu,
2008).
28
Finansal piyasalarda fiyatları hacmin etkilediğine ve hacmin boğa piyasasında
yüksek, ayı piyasasında düĢük olduğuna iliĢkin iki görüĢ bulunmaktadır. Birincisinde,
iĢlem hacmi ile getirilerin mutlak büyüklüğü arasında pozitif korelasyon olduğu,
ikincisinde ise hacim ile getiriler arasında pozitif korelasyon olduğu kabul edilmektedir
(Badhani ve Suyal, 2005).
Fiyat ve iĢlem hacmi iliĢkisinin önemi dört sebeple açıklanmıĢtır (Karpoff,
1987):
i. Fiyat-hacim iliĢkilerinden yararlanarak piyasanın genel yapısı hakkında bilgi
edinilebilir. Fiyat-hacim iliĢkisini konu alan modeller piyasaya giren bilginin
akıĢ hızı, bu bilginin nasıl yayıldığı, piyasa fiyatlarının bu bilgileri ne kadar
içerdiği, piyasanın büyüklüğü ve açığa satıĢ imkânı gibi piyasanın genel
yapısına ait pek çok faktörü göz önünde bulundurmaktadır.
ii. Fiyat-hacim iliĢkilerini beraber olarak inceleyen örnek olay çalıĢmalarından
önemli sonuçlar elde etmek mümkündür. Örneğin, fiyatlardaki değiĢimler
piyasaya yeni bir bilgi giriĢi olduğuna ve buna karĢılık gelen iĢlem
hacmindeki değiĢimin derecesi de yatırımcılar arasında bu yeni bilginin ne
kadar benzer kabul edildiğine dair bir kanıt olabilir.
iii. Fiyat-hacim iliĢkileri, fiyatların ne kadar spekülatif (kurgusal) olabileceği
konusunda fikir verebilir. Borsada yüksek getiriler ve büyük kayıplar
yaĢanma ihtimali yüksektir. Fiyatların varyansındaki değiĢimler iĢlem hacmi
tarafından açıklanabilir.
iv. Fiyat-hacim iliĢkileri vadeli iĢlemler piyasası için oldukça önemlidir.
ĠĢlem hacmi verilerini yorumlarken birçok teknik analiz yöntemi kullanılabilir.
Bu yöntemlerin ortak amacı, iĢlem hacmi ve fiyatını birlikte değerlendirerek, fiyattaki
olası yön değiĢtirmeleri önceden belirleyebilmektir. Bu yöntemlerden bir tanesi de
Toplama-dağıtım endeksi (Accumulation-Distribution Index)‟ dir.
Toplama-dağıtım endeksi iĢlem hacmi ve fiyatlardaki hareketleri birleĢtirerek,
fiyatların trendinin sürüp sürmeyeceği konusunda yatırımcılara fikir veren bir iĢlem
hacmi göstergesidir (Günak, 2007).
Bir fiyat hareketi ile beraber gerçekleĢen iĢlem hacminin fazlalığı, fiyat
hareketini o denli güvenilir yapmaktadır. Yani fiyat hareketinin bundan sonraki hareketi
de içinde bulunduğu trend yönünde gerçekleĢecektir. Bu düĢünceyle oluĢturulan
29
Toplama-dağıtım endeksinin yukarı gitmesi senedin toplandığı, aĢağı gitmesi ise
senedin dağıtıldığı anlamına gelmektedir (Apaydın, 2009). Toplama-dağıtım endeksi:
N
ADIi
i =1
(Ci - Li ) - (Hi - Ci )
.Vi
(Hi - Li )
(3.10)
eĢitliğiyle ifade edilir (Günak, 2007). Burada;
Ci : i hisse senedinin kapanıĢ fiyatı (Close),
Hi : i hisse senedinin en yüksek fiyatı (High),
L i : i hisse senedinin en düĢük fiyatı (Low),
Vi : i hisse senedinin adedi (Volume),
ADIi : i hisse senedinin Toplama-dağıtım endeksi (Accumulation-distribution index).
ADI endeksi pozitif ise göstergeye dahil edilir, negatif ise göstergeden çıkartılır.
Her gün için bu iĢlem devam edildiği taktide kesiksiz bir ADI eğrisi elde etmek
mümkün olacaktır.
Elde edilen ADI grafiğinde iki durum dikkatle incelenmektedir (Erdinç, 1998):
Gösterge belli bir dip noktaya ulaĢıp da tekrar yükselmeye baĢlarsa “al”
kararı, belli bir tepe yaptıktan sonra ise düĢmeye baĢlarsa “sat” kararı verilir.
Genellikle göstergenin dip yaptığı noktalarda o hisse senedinden çıkıĢlar
hızlanmıĢtır. Bu arada uzman yatırımcılar artık senedin daha fazla aĢağı
gitmeyeceğini görürler ve alıma geçerler. Aksi durumda ise, yani ADI
göstergesi önemli bir tepe noktasına ulaĢtığında hisse senedine talep çok
artmıĢtır ve küçük yatırımcı senede girmeye baĢladığında, uzman
yatırımcılar senedi elden çıkarmaya baĢlarlar ki bu da göstergeyi aĢağıya
çevirir.
Ġkinci önemli durum aykırılıkların analizidir. Eğer gösterge yukarı eğilim
içerisindeyken, fiyatlar aĢağı bir eğilime girmiĢse bir süre sonra fiyatların
artacağı, tersi durum olduğunda yani gösterge aĢağı eğilim yaparken,
fiyatlar yukarı eğilim içerisindeyse bir süre sonra fiyatların düĢeceği
düĢünülür.
30
3.7. Vadeli ĠĢlem ve Opsiyon Borsası
Vadeli ĠĢlem ve Opsiyon Borsası 4 ġubat 2005 tarihinde idari merkezi Ġzmir
olarak iĢlemlerine baĢlamıĢtır. Bu borsada “türev araç” veya sözleĢme alınıp
satılmaktadır. Döviz vadeli iĢlem sözleĢmeleri (Dolar, Euro), endeks vadeli iĢlem
sözleĢmeleri (ĠMKB 30, ĠMKB 100), faiz vadeli iĢlem sözleĢmeleri, emtia vadeli iĢlem
sözleĢmeleri (buğday, pamuk, altın) VOB‟ da iĢlem gören sözleĢmelerdir. Eğer
yatırımcı uzun vadeli düĢünüyorsa ve fiyatlar dalgalıysa VOB‟ a ihtiyaç var demektir.
Vadeli iĢlem sözleĢmeleri genellikle üç amaçla kullanılmaktadır;
i.
Korunma
ii.
Yatırım
iii.
Arbitraj
Vadeli ĠĢlem ve Opsiyon Borsası‟nın en önemli fonksiyonu, etkin risk yönetimi
ve geleceğe yönelik fiyat keĢfidir. Ülkemizde kurulmasının temel amacı ise,
iĢletmelerin risk yönetim ihtiyaçlarının en etkin Ģekilde karĢılamaktır. Buna paralel
olarak fiyat belirsizliğinin yaratacağı risklere karĢı etkin bir korunma imkanı
sağlamaktadır (Anonim, 2010).
Bireysel müĢterinin doğrudan borsada da iĢlem yapabilmesi mümkün değildir.
VOB‟ da iĢlem yapabilmek için,
i.
Aracı bir kuruluĢta hesap açtırmak gerekmektedir.
ii.
Vadeli ĠĢlem ve Opsiyon SözleĢmesi için alım-satım kararı verilmelidir.
iii.
Yatırımcının hesabında belli bir miktar iĢlem teminatı bulunmalıdır.
iv.
ĠĢlemi gerçekleĢtirmek için borsaya emir yollanmalıdır.
3.7.1. Opsiyon iĢlemleri
Bir finansal varlığın, gelecekte belirlenen bir tarihte veya belirli bir zaman süresi
içinde, prim karĢılığında, önceden belirlenmiĢ bir fiyattan satma veya satın alma hakkını
veren bir anlaĢmadır. Opsiyon sözleĢmesi, taraflardan birine anlaĢmadaki hakları
kullanmak veya bu haklardan vazgeçmek seçeneği tanırken, diğer taraftan hak sahibinin
sözleĢmedeki haklarını kullanmayı seçmesi durumunda, anlaĢmanın gereklerini yerine
getirme sorumluluğu yüklemektedir (Alpan, 1999).
31
Opsiyonları, gelecek veya vadeli iĢlemlerden ayıran ve daha avantajlı kılan en
önemli özellik, opsiyon sözleĢmesinde tanınan hakkın, kullanılıp kullanılmamasıdır
(Korkmaz, 1999).
Yatırımcılar açısından opsiyon piyasalarının sağladığı faydalar,
1. Küçük miktarda yatırımlarla temel piyasalarda elde edilebilecek karların çok
üzerinde getiri sağlayabilir.
2. Borçlanma ve borç verme durumunda daha avantajlı faiz oranları
sağlayabilir.
3. Daha uygun teminat Ģartları ile yatırım yapma imkanı sağlayabilir.
4. Temel piyasalarda elde edilemeyecek vergi avantajları sağlayabilir.
5. Opsiyon sözleĢmelerinde alım/satım maliyetleri daha düĢüktür.
6. Aynı risk düzeyinde olmasına rağmen daha yüksek getiri sağlayan portföy
oluĢturabilme imkanı verir.
7. Beklenmedik fiyat dalgalanmalarına karĢı korunma sağlar.
biçiminde sıralanabilir (Balaban, 1995).
3.7.2. Opsiyonların özellikleri
Satın alma opsiyonunun fiyatı,
Üzerine opsiyon yazılan finansal varlığın fiyat değiĢkenliğine ( σ )
Üzerine opsiyon yazılan finansal varlığın piyasa fiyatına ( S0 )
Opsiyonun vadesine kalan süreye ( T )
Risksiz faiz oranı ( r )
Opsiyonun kullanım fiyatına ( E )
parametrelerine bağlıdır (Alpan, 1999). Bir opsiyon sözleĢmesi,
Opsiyonun tipi: Avrupa veya Amerikan tipi
SözleĢme tipi: Alım (Call) opsiyonu veya Satım (Put) opsiyonu
Opsiyona konu mal veya kıymet: Hisse senedi, tahvil, endeks vb.
Kullanım fiyatı: Opsiyonun sağladığı hakkın kullanılacağı fiyat
Vade sonu
Prim: Opsiyonun fiyatı
32
bilgilerini içerir.
Opsiyon sözleĢmelerinde kullanılan bazı tanımlar aĢağıda verilmiĢtir:
Uzun Taraf: Alım opsiyonlarında primi ödeyen ve dolayısıyla dayanak varlığı
alma hakkını elde eden, satım opsiyonlarında ise, ödediği prim karĢısında dayanak
varlığı satma hakkını elde eden taraftır (Anonim, 2007).
Kısa Taraf: Alım opsiyonlarında opsiyon primini alan ve dayanak varlığı satma
yükümlülüğü altında olan, satım opsiyonlarında ise, dayanak varlığı alma yükümlülüğü
altında bulunan taraftır (Anonim, 2007).
Prim: Satıcının opsiyonu yazmak için talep ettiği fiyattır ve genelde iĢlem
anında tahsil edilmektedir. Opsiyon kullanılmadığı bir durumda ise alıcıya iade
edilmemektedir. Primler opsiyonun vadesine olan uzaklığına, opsiyona konu olan mal
veya finansal ürünün piyasa fiyatının opsiyonun kullanım fiyatı ile arasındaki farka,
fiyat dalgalanmalarının büyüklüğüne, risksiz faiz oranına ve sermaye kazancı dıĢındaki
getirilere göre değiĢiklik gösterir (Anonim, 2007).
Kullanım Fiyatı: Vade tarihinde hisse senedinin opsiyon anlaĢmasında belirtilen
satın alma fiyatı (Alpan, 1999).
3.7.3. Opsiyon sözleĢmelerinin türleri
Satın alma (call options) ve satma (put options) opsiyonları olmak üzere iki tür
opsiyon vardır.
i. Satın alma opsiyonu: Alıcısına, belirli bir hisse senedinden, belirli bir
miktarda, belirlenmiĢ bir tarihte veya öncesinde, belirli bir fiyattan satın
alma hakkı tanıyan fakat sorumluluk yüklemeyen sözleĢmedir. Satın alma
opsiyonunda, opsiyon yazıcısı, alıcının opsiyon hakkını kullanması
durumunda, sözleĢmede belirtilen hisse senedini satma zorunluluğundadır
(Korkmaz, 1999).
Yatırımcı ilgilendiği varlığın fiyatının yükseleceğini düĢünüyorsa bugünden
ilgili varlığın fiyatını sabitlemek için alım opsiyonu satın alır. Vade geldiğinde alıcı
taraf spot piyasadaki menkul kıymetin fiyatı ile opsiyon sözleĢmesindeki fiyatı
karĢılaĢtırarak opsiyonu kullanıp kullanmayacağına karar verir (Anonim, 2007). ġekil
3.3 ve ġekil 3.4 „ de satın alma opsiyonu durumunda alıcı ve satıcı pozisyonu için kar
33
ve zarar durumları gösterilmiĢtir. K, uzlaĢma (alım) fiyatını, C prim miktarını, S0 cari
pazar fiyatını göstermektedir.
Kar
K
0
S0
K+C
-C
Zarar
ġekil 3.3. Alım opsiyonda alıcının durumu (Balaban, 1995)
Kar
C
K+C
S0
0
K
Zarar
ġekil 3.4. Alım opsiyonunda satıcının durumu (Balaban, 1995)
ii. Satma Opsiyonu: Sahibine, belirli bir hisse senedinden belirli bir miktarda,
sözleĢmede belirtilen tarihte veya öncesinde, belirlenmiĢ bir fiyat üzerinden
satma hakkı tanır (Korkmaz, 1999).
Satım opsiyonu alan taraf ileride fiyatların düĢeceğini beklemektedir. Fiyatlar
düĢerse opsiyonu kullanır. Fiyatlar yükselirse opsiyonu kullanmaz. Bu durumda zararı
ödediği prim kadardır. Satım opsiyonu satan tarafın beklentisi ise fiyatların yükseleceği
yönündedir.
Opsiyonun
kullanılmayacağını
veya
fiyatın
aldığı
prim
kadar
34
yükselmeyeceğini düĢünmektedir. Satan tarafın amacı aldığı prim kadar kar elde
etmektir (Anonim, 2007). ġekil 3.5 ve ġekil 3.6 „ da satma opsiyonu durumunda alıcı ve
satıcı pozisyonu için kar ve zarar durumları gösterilmiĢtir. K, uzlaĢma (alım) fiyatını, P
prim miktarını, S0 cari pazar fiyatını göstermektedir.
Kar
K
0
S0
K-P
-P
Zarar
ġekil 3.5. Satma opsiyonunda alıcının durumu (Balaban, 1995)
Kar
P
K-P
0
K
Zarar
ġekil 3.6. Satma opsiyonunda satıcının durumu (Balaban, 1995)
S0
35
3.7.4. Black & Scholes opsiyon değerleme modeli
Bu model opsiyon değerlendirme modeli olarak bilinmektedir. Black & Scholes
modeli, satın alma opsiyonunun fiyatını hesaplamayı sağlayan değiĢkenler arasındaki
bağıntıyı ifade etmektedir (Alpan, 1999).
Black & Scholes modelinin diğer modellere göre daha basit ve uygulanabilir
olması nedeniyle günümüzde opsiyon piyasası oyuncuları arasında Black & Scholes
opsiyon modeli versiyonuna sahip olan makineler ve programlar sıkça kullanarak, hisse
senedi opsiyonunun uygun değerini hesaplamaktadırlar.
Black & Scholes modelinin matematiksel formülü,
VC
d1
d2
C S0 N(d1 ) Ee
rT
N(d 2 )
ln(S0 /E) (r (1/2)σ 2 )T
σ T
d1 σ T
eĢitlikleriyle gösterilir (Alpan, 1999). Burada;
VC : Satın alma opsiyonunun fiyatı,
N(d1 ), N(d 2 ) : Normal dağılım tablosunda d1 ve d2 ‟ ye karĢılık gelen değerler,
S0 : Cari hisse senedi (endeks) fiyatı,
E
: Opsiyon kullanma fiyatı,
r
: Risksiz faiz oranı,
σ
: Hisse senedinin getiri oranlarının yıllık standart sapması,
T : Opsiyonun bitimine kadar kalan zaman,
: Doğal logaritma fonksiyonunun tabanı,
e
e
ln
rT
: Ġskonto oranı,
: Doğal logaritma fonksiyonu.
(3.11)
(3.12)
(3.13)
36
Bu modelin bazı temel varsayımları,
Opsiyon alım ve satımında herhangi bir iĢlem maliyeti yoktur ve vergi söz
konusu değildir.
Kısa bir zaman içerisinde hisse senedinin fiyatında sadece küçük bir
değiĢiklik olmaktadır.
Menkul kıymetlerin fiyatları arbitraja imkan vermemektedir.
Hisse senetlerinin fiyatları sürekli olarak değiĢmektedir.
Hisse senedi getirileri logaritmik normal dağılım Ģeklindedir.
Opsiyon Avrupa tipi satın alma opsiyonudur.
Vade içerisindeki opsiyona konu olan hisse senedi için herhangi bir kar payı
ödemesi yoktur.
Kısa vadeli faiz oranı bilinmekte ve opsiyonun vadesi boyunca
değiĢmemektedir.
Hisse senedinin riski opsiyonun vadesi boyunca değiĢmemektedir.
olarak verilebilir (Tural, 2008).
3.8. Portföy Seçim Teorileri
Literatürde geleneksel portföy yaklaĢımı ve modern portföy yaklaĢımı olmak
üzere iki çeĢit portföy seçim yaklaĢımı bulunmaktadır. Bu kısımda, portföy seçim
yaklaĢımları açıklanmıĢ, Markowitz modeli ve Konno – Yamazaki modeli incelenmiĢtir.
3.8.1. Geleneksel portföy yaklaĢımı
Geleneksel portföy yaklaĢımı, 1950‟li yıllara kadar hem teoride hem de pratikte
yaygın olarak kullanılmıĢtır. Yöntemin bilimsel bir dayanağı olmamasına rağmen,
uygulama kolaylığı olmasından dolayı birçok yatırımcı tarafından hala kullanılmaktadır.
Bu yaklaĢım, aĢırı çeĢitlendirmeye önem vermekte ve portföye alınacak olan menkul
kıymetler arasında olası iliĢkileri dikkate almamaktadır (Bekçi, 2001).
37
Geleneksel portföy yaklaĢımında portföyün getirisi, portföyü oluĢturan menkul
kıymetlerin temettü ve belli bir dönemdeki değer artıĢıdır. Bu nedenle, yatırımcıların
gelecekteki menkul kıymet getirilerini tahmin etmeleri gerekmektedir. Portföyü
oluĢturan menkul kıymetlerin getirileri aynı yönde hareket etmeyeceğinden, portföyün
riski tek bir menkul kıymetin riskinden küçük olacaktır. ĠĢte, geleneksel portföy teorisi,
bu prensipten hareketle, portföy içindeki menkul kıymet sayısının arttırılması ilkesine
dayanır. Bu yaklaĢımı, “bütün yumurtaları aynı sepete koymamak” Ģeklinde
tanımlamakta mümkündür. Genel olarak yatırımcıların amaçları, sabit ve istikrarlı gelir
elde etmek, sermayenin korunması veya sermaye kazancı elde etmek gibi ifade
edilebilir (Ceylan ve Korkmaz, 1998).
Geleneksel portföy yaklaĢımında aĢamalar,
i. Yatırımcıya ait bilgilerin toplanması,
ii. Portföy amacının saptanması,
iii. Yatırım politikaları,
iv. Portföye dahil edilecek menkul kıymetlerin seçilmesi.
biçimindedir.
3.8.2. Modern portföy yaklaĢımı
Modern portföy yaklaĢımında, sadece portföy çeĢitlendirmesine gidilerek riskin
azaltılamayacağı, çünkü, portföyde yer alan menkul kıymetlerin ya da menkul kıymet
gruplarının, aynı ya da ters yönde hareket ettikleri ileri sürülmektedir (Ceylan ve
Korkmaz, 1998).
Bazı yatırımcılar ve portföy yöneticileri, tek tek menkul kıymetler ya da gruplar
arasında, aynı ya da zıt yönde bir hareket olduğunu belirlemiĢler ancak bu iliĢkiyi
ölçebilecek formül veya teknikler geliĢtirememiĢlerdir. Modern portföy teorisinin
mimarı diyebileceğimiz Harry Markowitz, bu iliĢkinin ölçülmesini sağlayan ve kendi
adı ile anılan modeli geliĢtirmiĢtir. Markowitz (1952), “Portföy Seçimi” adlı
makalesinde, portföyü oluĢturan menkul varlıklar arasındaki iliĢkinin araĢtırılması ve
getirileri arasında tam pozitif korelasyon bulunmayan menkul kıymetlerle bir portföy
oluĢturulması suretiyle beklenen getiride bir azalma olmaksızın, sistematik olmayan
riskin düĢürülebileceği görüĢünü ileri sürmüĢtür (Ġpekten, 1992).
38
Modern portföy teorisi, piyasada bilgilerin nasıl değerlendirildiği, yatırımcıların
nasıl davrandığı, yatırımcıların davranıĢlarının fiyat oluĢumlarını nasıl etkilediği ve bu
iliĢkilerin nasıl nicelleĢtirilebileceğiyle uğraĢan birkaç varsayıma dayanmaktadır.
Bunları;
-
Menkul kıymetler borsalarında iĢlem gören menkul kıymetlerin arzında
herhangi bir kısıtlama söz konusu değildir. Dolayısıyla yatırımcılar borsada
istediği kadar hisse senedi alabilme imkânına sahiptir.
-
Menkul kıymet yatırımcıları, akıllı hareket etmeyi düĢünürler. Yani
yatırımcının en büyük amacı, elde edebileceği faydayı maksimum yapmaktır.
Dolayısıyla, kendi refahlarını arttırmaktır.
-
Menkul kıymet yatırımcıları, yatırım kararı verdiklerinde bunu yatırım
yapacakları menkul kıymetlerin beklenen getirisi ve risklerine göre yaparlar.
Beklenen getiri ölçüsü olarak portföy içindeki menkul kıymetlerin beklenen
getirilerinin ortalamasını, risk ölçüsü olarak da portföy getirilerinin
varyansını alırlar. Dolayısıyla yatırımcıların tümü menkul kıymetlerin
beklenen getirileri, standart sapmaları ve korelasyonuna iliĢkin aynı
beklentiye sahiptirler.
-
Menkul kıymet yatırımcılarının hemen hemen tümü, aynı risk düzeyinde
daha fazla getiri elde etmeyi tercih ederler.
-
Menkul kıymet yatırımcıları, aynı zaman ufkuna sahiptirler.
-
Menkul kıymet yatırımcıları için sermaye piyasasına ait bilgilere aynı
zamanda ulaĢmak mümkündür. Çünkü sermaye piyasası bilgileri süratle ve
doğru olarak menkul kıymet fiyatlarına yansımaktadır. Bilgi akıĢına ait bir
kısıtlama yoktur.
Ģeklinde sıralamak mümkündür (Berk, 2000).
3.8.2.1. Markowitz (Ortalama - Varyans) modeli
Markowitz, 1952 yılında yayımladığı “Portfolio Selection” adlı makalesi ile
portföy analizinde yeni bir çağ açmıĢtır. Bu çalıĢmadaki amaç, yatırımcının kazancını
maksimum, riskini ise minimum yapan portföylerin seçimini, olabilirlik ve
39
optimizasyon teknikleri yardımıyla sağlamaktır. Bu Ģekilde yatırımları çeĢitli
alternatifler üzerinde değerlendirme fikrinin ilk matematiksel formülünü oluĢturmuĢtur.
Markowitz modeli, kovaryans ile tanımlanan portföy riskinin en küçüklenmesi
ve portföyün beklenen getirisinin en büyüklenmesi kararları Ģeklinde iki temel ölçü
içerir (Markowitz, 1952).
Markowitz modeline göre çeĢitlendirmenin temel yaklaĢımı “çok sayıda menkul
kıymete” değil, “doğru menkul kıymete” yatırım yapmaktır. Markowitz, bu durumu
Ģöyle ifade eder; Portföy analizi, yalnızca çeĢitlendirmeyi içermez; aynı zamanda doğru
bir sebep için doğru çeĢitlendirmeyi içerir. ÇeĢitlendirmenin yetersizliği, yatırımcılar
tarafından, elde tutulan menkul kıymetlerin sayısına bağlı olarak değerlendirilemez.
Örneğin, 60 değiĢik demiryolu menkulünden oluĢan bir portföy, demiryolu, hizmet,
maden ve çeĢitli üretim sektörlerinden oluĢan aynı sayıdaki menkulü içeren portföy
kadar iyi çeĢitlendirilmiĢ olmayacaktır. Bunun nedeni, aynı endüstrideki firmaların aynı
anda güçsüzleĢmesinin farklı endüstrideki firmalardan daha muhtemel olmasıdır.
Benzer Ģekilde, getirilerinin varyansını küçültmeye çalıĢırken, çok sayıda menkul
kıymete yatırım yapmak yeterli değildir. Aralarında yüksek kovaryans olan menkul
kıymetlere yatırım yapmaktan çekinmek gerekir (Pelitli, 2007).
Modern portföy modelinin varsayımları,
Yatırımcının amacı, fayda fonksiyonunu maksimize etmektir.
Yatırımcı, yatırım kararını, risk ve getiriyi esas alarak verir. Getiri ölçütü
olarak, portföyü oluĢturan varlıkların beklenen getirilerinin ortalaması,
riskin ölçütü olarak da bu portföy getirilerinin varyansı kullanılır.
Yatırımcıların risk ve getiri hakkındaki beklentileri homojendir.
Yatırımcılar özdeĢ, zaman ufkuna sahiptir.
Bilgi akıĢına herhangi bir kısıtlama konmamıĢtır ve yatırımcılar için söz
konusu bilgilere eĢ zamanlı olarak ulaĢmak mümkündür.
olarak sıralanabilir (Yörük, 2000).
Markowitz modelinin amaç fonksiyonu;
N
V
N
Min
x i x jσij
i =1 j =1
biçiminde gösterilmektedir (Markowitz, 1952). Burada;
V : Portföyün varyansı,
N : Mevcut varlık (menkul kıymet) sayısı,
(3.14)
40
σ ij : i ve j menkul kıymetler arasındaki kovaryans değeri (i=1,…,N) (j=1,…,N),
x i : i menkul kıymetinin portföy içindeki oranı,
x j : j menkul kıymetinin portföy içindeki oranı,
Markowitz modelinde iki temel kısıt vardır. Bunlardan birincisi, hedeflenen
beklenen getiri düzeyini sağlayacak kısıttır ve matematiksel ifadesi;
N
x iμ i
R
(3.15)
i =1
„dir. Burada;
μ i : i menkul kıymetinin beklenen getirisi (i=1,…,N),
x i : i menkul kıymetinin portföy içindeki ağırlığı,
R : Beklenen getiri.
Modelin ikinci temel kısıtı, portföyde bulunan menkul kıymetlerin ağırlıklarının
toplamının 1‟ e eĢit olmasıdır.
N
xi
1
i =1
Yatırım içerisindeki menkul kıymetlerin ağırlıkları aĢağıdaki eĢitsizlik biçiminde
ifade edilir;
0 ≤ xi ≤ 1
i=1,…,N
Markowitz modeline göre; iki menkul kıymetten ve N sayıda menkul kıymetten
oluĢan portföylerin beklenen getirileri ve varyansları aĢağıdaki Ģekilde hesaplanabilir:
1.İki menkul kıymetten oluşan portföyler: Bir portföyün sadece iki menkul
kıymetten oluĢmayacağı, optimal bir portföyde bulunacak menkul kıymet sayısı
hakkında tam ve kesin bir rakamın olmadığı bilinmektedir. AĢağıda iki menkul
kıymetten oluĢan portföyün beklenen getirisi ve riski verilmiĢtir:
E(R p ) = x 1 .E(R 1 ) + x 2 .E(R 2 )
(3.16)
σP
(3.17)
x12 .σ12 +x 22 .σ 22 +2.x1.x 2 .σ1.σ 2 .ρ12
Burada;
E(R1 ) : Birinci menkul kıymetin beklenen getirisi,
41
E(R 2 ) : Ġkinci menkul kıymetin beklenen getirisi,
E(R p ) : Portföyün getirisi,
σ1
: Birinci menkul kıymetin standart sapması,
σ2
: Ġkinci menkul kıymetin standart sapması,
x1
: Birinci menkul kıymetin portföy içindeki ağırlığı,
x2
: Ġkinci menkul kıymetin portföy içindeki ağırlığı,
ρ12
: Birinci ve ikinci menkul kıymet arasındaki korelasyon katsayısı,
σP
: Portföyün kovaryansı (Riski).
Portföyün getirisi, tek tek menkul kıymetlerin getirilerinin ağırlıklı ortalamasıdır.
Portföyün riski ise portföyü oluĢturan menkul kıymetlerin getirilerinin varyansları ile bu
getiriler arasındaki kovaryansın iliĢkisine bağlı olarak değiĢmektedir. Portföye dahil
edilen menkul kıymetler arasındaki iliĢki, korelasyon katsayısı ile gösterilir.
Korelasyon katsayısının +1 olması durumu: Portföyü oluĢturan menkul
kıymetlerin getirileri arasındaki korelasyonun tam olması durumunda, portföy riskini
sınırlamak mümkün değildir. Çünkü portföydeki menkul kıymetlerin fiyatları aynı
yönde değiĢmektedir. BaĢka bir deyiĢle, portföy tek bir menkul kıymetten oluĢmuĢ
gibidir (Ceylan ve Korkmaz, 1998).
Beklenen Getiri
20
B
15
10
5
A
Risk
ġekil 3.7. Korelasyon katsayısının +1 olması durumunda portföy riski (Ceylan ve Korkmaz, 1998)
42
Korelasyon katsayısının sıfır olması durumu: Portföyü oluĢturan menkul
kıymetlerin getirileri arasında herhangi bir iliĢki bulunmuyorsa, çeĢitlendirme yoluyla
risk azaltılabilir. Korelasyon katsayısının sıfır olması durumunda, portföy riskinde
görülen sınırlama, portföy riskine iliĢkin eĢitlik üzerinde de izlenebilir. Korelasyonun
sıfır olması durumunda formülün üçüncü terimi sıfıra eĢit olacaktır. Bu durumda, iki
menkul kıymetten oluĢan portföyün standart sapması,
σP
x12 .σ12 +x 22 .σ 22
(3.18)
eĢitliğiyle ifade edilmektedir. ġekil 3.8‟ de korelasyon katsayısının sıfır olması
durumunda portföy riski gösterilmiĢtir.
Beklenen Getiri
B
A
Risk
ġekil 3.8. Korelasyon katsayısının sıfır olması durumunda portföy riski (Ceylan ve Korkmaz, 1998)
Korelasyon katsayısının -1 olması durumu: Menkul kıymetlerin getirileri
arasındaki iliĢkinin negatif olması ihtimali en az rastlanan bir durumdur. Korelasyon
katsayısının negatif olması halinde, portföy riski minimum düzeye indirilebilir. Eğer
korelasyon katsayısı -1 ise, menkul kıymetler arasında mükemmel negatif tam
korelasyon var demektir. Bu durumda portföy riski, belirli bir menkul kıymet
bileĢiminde sıfır olacaktır. Portföy çeĢitlendirmesinde menkul kıymetler arasındaki
korelasyon katsayısının -1 veya yakın bir değerde olması arzu edilir. Ancak piyasada
her zaman korelasyon katsayısı -1 veya bu değere yakın menkul kıymetler bulmak
43
mümkün değildir. ġekil 3.9‟ da Z noktası risksiz portföy bileĢimini göstermektedir
(Ceylan ve Korkmaz, 1998).
Beklenen Getiri
20
B
17
10
Z
5
A
Risk
ġekil 3.9. Korelasyon katsayısının -1 olması durumunda portföy riski (Ceylan ve Korkmaz, 1998)
Korelasyon katsayısının +1, 0 ve -1 olması durumu tek bir grafik üzerinde ġekil
3.10‟ da gösterilmiĢtir.
Beklenen Getiri
20
B
17
r = -1
r=0
10
Z
5
r = +1
C
A
Risk
ġekil 3.10. Korelasyon katsayısının +1, 0 ve -1 olması durumunda portföy riski (Ceylan ve Korkmaz,
1998)
44
2. N sayıda menkul kıymetten oluşan portföyler: Gerçek hayatta yatırımcıların
portföylerine alacağı ve hakkında bilgi sahibi olması gereken yüzlerce finansal varlık
vardır. Bu nedenle, N sayıda menkul kıymetten oluĢan portföyün beklenen getirilerinin
ve risklerinin hesaplanması gerekmektedir. Ancak menkul kıymetler arasındaki
korelasyonların hesaplanmasında bazı sorunlar görülmektedir. Menkul kıymetler
arasındaki korelasyon sayısı, menkul kıymet artıĢından daha fazla olmaktadır.
Hesaplamalarda
kullanılan
değiĢkenlerin
sayısı
arttıkça,
iĢlemlerin
yapılması
zorlaĢmakta, hatta iĢlemlerin elle yapılması imkânsızlaĢmaktadır. Bu nedenle bu tür
iĢlemler için hazırlanmıĢ bilgi iĢlem programlarından yararlanılmaktadır. Bilindiği gibi,
N sayıda menkul kıymet bulunan bir portföyde, menkul kıymetlere değiĢik ağırlıklar
verilerek, sınırsız sayıda portföy oluĢturulabilir. Bu nedenle,
yatırımcının baĢlıca
görevi, belirli bir beklenen getiri oranı düzeyinde, kovaryansların ağırlıklı ortalamasını
mümkün olduğu kadar düĢürecek bir biçimde, parasını menkul kıymetler arasında
paylaĢtırabilmek için “etkin portföyleri” seçmektir. Eğer yatırımcılar, varyansı göz
önüne almaksızın, sadece beklene getiriyi maksimize etmek isterlerse, fonlarını en az
getiri sağlayacak olan tek bir menkul kıymete yatıracaklardır. Öte yandan, eğer
yatırımcılar, varyansın en aza indirilmesiyle ilgileniyorlarsa ve beklenen getiriyi göz
ardı
ediyorlarsa,
Portföylerindeki
bir
her
portföy
bir
menkul
aracılığı
ile
kıymetin
yatırımlarını
payını
ise
çeĢitlendirecektir.
matematiksel
olarak
saptayacaklardır. Markowitz, değiĢik risk ve getiri düzeylerindeki etkin portföyleri
birleĢtiren eğriyi “etkin sınır” olarak tanımlamıĢ ve portföy yöneticisinin amacını “etkin
sınır üzerindeki noktaları belirlemek” olarak ifade etmiĢtir (Ceylan ve Korkmaz, 1998).
3.8.2.2. Markowitz modeline göre optimal portföyler ve etkin sınır
Bir portföyün optimal olarak nitelendirilebilmesi için belli bir kârlılık
seviyesinde riskinin en düĢük veya belli bir risk altında kârlılığının en yüksek olması
gerekir. Yatırımcılar açısından optimal portföyler listesinden risk ve kârlılık bileĢimi
amacına en uygun olan portföyü seçmek önemlidir.
Portföy oluĢturmada riski en aza indirmeye çalıĢmak çok fazla gerekli değildir.
Çünkü risk azaltılırken, beklenen getiri de azaltılmıĢ olacaktır. Bundan dolayı, en uygun
45
risk ve getiri bileĢimini elde etmek önemlidir. En uygun risk ve getiri bileĢimine sahip
olan portföy, optimal portföydür.
Markowitz modeli kullanılarak optimal portföy seti belirlenir. Daha sonra
yatırımcılar, oluĢturulan bu set içinde yer alan portföylerden hangisini tercih
edeceklerine karar verebilirler. Bu model sadece tek bir optimal portföy sağlamaz.
Aksine, en iyi olan optimal portföylerin sınırlarını oluĢturmaktadır. Optimal portföy
setleri oluĢturabilmek için portföye alınabilecek her bir menkul kıymetin beklenen
getirisi, menkul kıymetlerin varyansı veya standart sapması, menkul kıymet getirileri
arasındaki iliĢkiyi gösteren kovaryans gibi birtakım bilgilere ihtiyaç vardır. Bu
bilgilerden hareketle optimal bir portföy, aynı risk seviyesindeki bütün portföyler içinde
en yüksek getiriye sahip olan veya aynı getiri seviyesinde riski en düĢük olan portföydür
(Bekçi, 2001). Optimal portföyler risk getiri uzayında ġekil 3.11‟ de görüldüğü gibi
etkin sınırı oluĢturur.
Yatırımcıların çoğu, uzun dönemli portföy yönetimini ve kazanç elde edecekleri
menkul kıymetleri seçmeyi isterler. Optimal portföyün ağırlığı menkul kıymetlerin
tahmin edilen bazı istatistiksel özelliklerine de bağlıdır. Bu bilgiler ıĢığında yatırımcılar
ellerindeki menkul kıymetlerin elde tutma süresini belirleyebilirler. Beklenen getiriler
ve bu getiriler arasındaki kovaryansların gerçek istatistiksel dağılımı hakkında bazı
yatırımcıların bilgisi olmayabilir. Bu nedenle bütün yatırımcılar aynı fayda
fonksiyonuna sahip olsa bile, optimal portföy oluĢturma konusu yatırımcıdan
yatırımcıya farklılık gösterebilecektir (Jacobs ve ark., 1999).
Y
Getiri (%)
Olanaksız Portföyler
Olanaksız Portföyler
Y
Olası Portföyler
Olası Portföyler
Olanaksız Portföyler
Olanaksız Portföyler
D
D
Risk (%)
ġekil 3.11. Etkin sınır veya portföy olanakları eğrisi (Genel, 2004)
46
Grafikte D-Y eğrisinin altında kalan taralı alan geçerli yatırım ortamında
oluĢturulabilecek portföylerin oluĢturduğu risk-getiri uzayını göstermektedir. Bunun
dıĢında kalan bölgede portföy oluĢturmak olanaksızdır. Taralı alandaki her noktada ise,
o noktaya karĢılık gelen risk ve beklenen getiriye sahip en az bir portföy oluĢturulabilir.
UlaĢılabilir alanın üstünü çevreleyen D-Y eğrisi ise etkin sınırı oluĢturur. Etkin sınır
üzerindeki portföyler hem belli bir beklenen getiri için en düĢük riske sahip olmaları,
hem de belli bir risk için en yüksek beklenen getiriye sahip olmaları nedeniyle
optimaldirler ve en iyi çeĢitlendirilmiĢ portföylerdir (Genel, 2004).
3.8.2.3. Modern portföy yaklaĢımına göre optimizasyon süreci
Modern portföy teorisi normatif bir teoridir. Pozitif teoriler gerçek yatırımcı
davranıĢlarını ele alırken, normatif teoriler yatırımcıların nasıl davranması gerektiğini
belirtir. Bu yönüyle, normatif bir teori olarak modern portföy teorisi optimum portföy
oluĢturmak amacıyla yatırımcının takip etmesi gereken standart veya normal davranıĢı
açıklamaktadır (Genel, 2004).
Modern portföy teorisine göre yatırım süreci ġekil 3.12‟ de gösterilmiĢtir.
Yatırımcı belirlediği beklenen getiri ve risk tahminleri ile portföy kısıtlarını kullanarak
optimal portföylerden oluĢan etkin sınırı oluĢturduktan sonra yatırım tercihleri
doğrultusunda yatırım yapacağı optimal portföyü seçer.
Yatırımcı
Tercihleri
Beklenen Getiri
Modeli
Risk ve Korelasyon
Tahminleri
Portföy Kısıtları
Portföy
Optimizasyonu
Etkin Sınır
Optimal Portföy
ġekil 3.12. Modern portföy teorisine göre yatırım süreci (Genel, 2004)
47
Etkin sınır, birçok portföyün risk ve getiri düzeyinde belirlenmesiyle elde edilir.
Yani, birçok menkul kıymetin var olduğu bir ortamda, oluĢturulacak portföy bileĢeni
için yatırım fırsatları kümesi oluĢturulur. OluĢturulan bu kümenin üst sınırına etkin sınır
denir. Bu etkin sınırın elde edilmesi için de portföyün varyansı ve beklenen getirisinin
bilinmesi gerekir. Bu nedenle üst sınır üzerinde oluĢan portföylere etkin portföyler denir
(Bekçi, 2001).
Portföy yöneticisi de etkin sınır üzerindeki etkin varlıklardan oluĢan
portföylerden hangilerinin seçileceği konusunda karar verirken, yatırımcı tipini göz
önüne almalıdır.
3.8.2.4. Konno-Yamazaki doğrusal programlama modeli
Konno–Yamazaki portföy modeli, beklenen bir getiri seviyesinde ortalama
getirisinden ( rj ) sapması en küçük hisse senetlerini belirleme de etkin bir yöntemdir ve
sadece belirli bir getiri seviyesindeki anı fotoğraflamaktadır. Yani, çözümler ortalama
getirisi
beklenen
getiri
seviyesine
eĢit
veya
en
yakın
hisse
senetlerinde
yoğunlaĢmaktadır (Kocadağlı, 2006).
Markowitz modeli, büyük ölçekli optimizasyon problemleri için uygun değildir.
Konno ve Yamazaki bunun nedenlerini Ģu Ģekilde sıralamıĢlardır;
-
Hesaplama yükü sorunu,
-
Risk ve hisse senedi fiyatları dağılımına karĢı yatırımcının algısı problemi,
-
ĠĢlem maliyeti problemi.
Bu aksaklıkları gidermek için Konno ve Yamazaki aĢağıdaki modeli geliĢtirmiĢlerdir
(Chang, 2005).
T
Amaç Fonksiyonu:
MinZ
yt / T
t =1
n
Kısıt 1:
yt
a tj x j
0
t =1,2,...,T
a tj x j
0
t =1,2,...,T
j =1
n
Kısıt 2:
yt
j =1
(3.19)
48
n
Kısıt 3:
rj x j
ρM 0
j =1
n
Kısıt 4:
x j = M0
j =1
0
xj
yt
0
uj
j =1,2,...,n
t =1,2,...,T
Burada;
T
: Ġncelenen dönem sayısı,
t
: T dönemi içindeki herhangi bir t. dönem,
ρ
: Beklenen getiri oranı,
rj
: j. hisse senedinin ortalama getiri oranı,
rj t : t dönemi boyunca j. hisse senedi için gerçekleĢen getiri oranı,
a tj : j. hisse senedinin riski ( rj t - rj ),
xj
: j. hisse senedine yapılan yatırımın payı,
uj
: j. hisse senedine yapılan yatırımın üst sınırı,
M0 : Toplam yatırım miktarı,
ρM0 : Beklenen getiri miktarı,
yt
: Yardımcı değiĢken.
olmak üzere a tj , j. hisse senedinin t. dönemde gerçekleĢen getiri oranı ile T dönemdeki
beklenen getiri oranı arasındaki farktır. Bu fark ortalamadan sapmadır ve riski ifade
eder (Konno ve Yamazaki, 1991).
Modeldeki amaç fonksiyonu, beklenen getiriden sapma ( ρ ) olarak ifade edilen
riski minimize etmek için kullanılmaktadır. Konno-Yamazaki modelinin etkinlik
sınırının her bir noktasının belirlenebilmesi için, eğer u j
ve j =1,2,...,n ise kısıt
sayısı en fazla “2T+2” olmalıdır. Yukarıdaki modelin 1. ve 2. eĢitsizlikleri her t dönemi
boyunca tekrarlanarak 2T tane kısıt elde edilir. Kısıtların iĢlevleri Ģöyledir: Amaç
fonksiyonu ve birinci eĢitsizlikten elde edilen T kısıt yardımıyla a tj katsayısı en küçük
olan hisse senetleri belirlenir. Ġkinci eĢitsizlikten elde edilen T kısıt yardımıyla, her t
49
dönemi için riski en az sıfıra eĢit hisse senetleri belirlenerek negatif sapmalı hisse
senetleri elimine edilecektir. Üçüncü kısıt yardımıyla da bu hisse senetlerinden ortalama
getiri oranı, beklenen getiriye eĢit ve en yakın (beklenen getiriyi aĢacak Ģekilde) olanlar
seçilecektir. Örneğin, t. dönemde yt yardımcı değiĢkeni minimize edilerek, ortalama
getirisi beklenen getirinin altında olmamak koĢuluyla a tj katsayısı en küçük olan, yani
riski en küçük x j ‟ ler belirlenir. Dördüncü kısıt ise toplam yatırımın miktarıdır. Son
olarak x j ve yt ‟ ler çözüm tekniği gereği sıfır veya sıfırdan büyük olmalıdır
(Kocadağlı, 2006).
3.8.3. Bulanık doğrusal programlama ile portföy seçimi yaklaĢımı
Günümüzde, geleneksel ve modern portföy yaklaĢımlarına ek olarak bulanık
mantık yaklaĢımı da portföy seçimi problemine adapte edilmiĢ, bu çerçevede birçok
çalıĢma yapılmıĢtır. KuĢkusuz bulanık mantık teorisi birçok alanda kullanıldığı gibi,
geleneksel ve modern portföy yaklaĢımlarını gölgede bırakacak sonuçlar alınmasına
imkan sağlamaktadır. Bu kısımda, bulanık mantık teorisi ve bulanık doğrusal
programlama modeli açıklanmıĢ daha sonra da BDP problemlerine çözüm yaklaĢımları
incelenmiĢtir.
3.8.3.1. Bulanık küme teorisi
Bulunduğumuz yüzyılın baĢında, kesin olan matematiksel modellemede yer alan
karmaĢık hayat sistemleri, bilim ve teknikte temel akımları oluĢturmaktaydı. Yüzyılın
ortalarına doğru ise, yöneylem araĢtırması gerçek hayat karar verme problemlerinde
uygulanmaya baĢladı ve böylelikle bilim ve teknikte en önemli alanlardan biri oldu.
Maalesef, gerçek dünya durumları genellikle o kadar deterministik olmadığı için kesin
olan matematiksel modeller, bütün uygulamalı problemlerin çözümü için yeterli değildir
(Eroğlu, 2006).
50
Bilimsel çalıĢmaların yapılmasında son 30 yıla kadar sadece iki çıktılı olan
Aristo mantığı kullanılmıĢtır. Buna göre incelenen olayın sadece ikili alternatif teĢkil
eden sonuçlarının olması mümkündür. Kısaca söylemek gerekirse sadece siyah veya
beyaz çıktılarından bir tanesini tercih etmek gereklidir. Hâlbuki insanın düĢünce
sisteminde arada olan değiĢik derecede gri tercihlerinde yapılması söz konusudur. ĠĢte
buna imkân verecek olan bulanık (fuzzy) mantık ve ondan kaynaklanan sistemler ilk
defa Azerbaycanlı L.A. Zadeh tarafından 1965 yılında ortaya atılmıĢtır (ġen, 2004).
Kesin matematik yöntemleri karmaĢık bir sistemi modellemek için yeterli
değildir. Geleneksel olarak olasılık teorisi belirsizlik altındaki durumları ele almak için
etkili bir yaklaĢımdır. Olasılık teorisinde temel esaslardan biri bir A olayı için
P( A
Ac ) 1 yasası, diğeri ise P( A
Ac ) 0 yasasıdır. Buna örnek olarak, bir meyve
ya elmadır ya değildir, bir hayvan ya diĢidir ya değildir. Bu durumda olasılık teorisi
sınırları açık bir Ģekilde tanımlanabilen bilgileri anlatmada kesin olarak etkili bir
yaklaĢımdır. Havaya atılan bir madeni para için, yazı mı yoksa tura mı geleceği tahmin
edebilir. Aynı Ģekilde oyun zarı için sonuçlar 1, 2, 3, 4, 5, 6 olacaktır. Ama asla 2,1 veya
4.5 gibi sonuçlar elde edilemez. Tabi ki bahsedilen olasılık yasalarına uygun birçok
problem vardır. Fakat sezgisel olarak diğer problemlerde bu yasalar geçerli değildir.
Örneğin, bir kiĢi Ģık olabilir, Ģık olmayabilir veya biraz Ģık olabilir. Aynı Ģekilde bir
renk kırmızı olabilir, kırmızı olmayabilir veya kırmızımtırak olabilir. Bu nedenle Ģık
kiĢiler ya da kırmızı renkler kümesini kesin sınırlarla tanımlamak zordur. Benzer olarak,
”güzel bir bayan”, “iyi bir lezzet”, “iyi bir kiĢilik”, “makul bir fiyat” vb. önermeleri
tanımlamak ve sınıflandırmak zordur. Açık olarak olasılık teorisi bu Ģekilde tüm olası
problemleri modelleyemez. Bulanık küme teorisi, kesin sınırları olmayan problemleri
tanımlamak ve çözmek için geliĢtirilmiĢtir (Eroğlu, 2006).
Bulanık mantığın en geçerli olduğu iki durumdan ilki, incelenen olayın çok
karmaĢık olması ve bununla ilgili yeterli bilginin bulunmaması durumunda kiĢilerin
görüĢ ve değer yargılarına yer vermesi, ikincisi ise insan muhakemesine, kavrayıĢlarına
ve karar vermesine ihtiyaç gösteren hallerdir (ġen, 2004).
Geleneksel ve bulanık kümeler sınır koĢulu ve üyelik derecesi anlamında
karĢılaĢtırılır. Bir örnekle açıklanmaya çalıĢıldığında, bir kümenin sınırları “lastik bir
bant” olarak kabul edilir, geleneksel küme durumunda lastik bantta herhangi bir
esnemeye izin verilmez ve bant sabit olarak kabul edilir. Bu nedenle, evrensel kümenin
her bir elemanı lastik bandın ya içinde ya da dıĢında kalır. Bununla birlikte, bulanık
51
kümeler durumunda lastik bandın dıĢında kalan yer alan nesneleri (noktaları) kümenin
elemanı yapabilmek için bandın esnetilmesine yani küme üyeliğini belirleyen sınır
koĢulunun gevĢetilmesine izin verilir. Bu esnemenin boyutu yeni noktanın konumuna
bağlıdır. Bant esnetilmeden önce bandın oluĢturduğu sınırın içinde bulunan noktalar 1
üyelik derecesi ile kümenin elemanıdır. Bant esnetildikçe kümeye üye olan veya bandın
içine girmeye baĢlayan noktalara, 0 ve 1 arasındaki üyelik dereceleri verilir. Herhangi
bir noktanın üyelik derecesi, lastik bandı esnetmek için gerekli olan güçle ters orantılı
olarak açıklanabilir. Bandın esneme oranı arttıkça ilgili elemanın üyelik derecesi azalır.
Bu nedenle, bandın oluĢturduğu sınırın içinde bulunan elemanlardan, sınırın dıĢında
kalan elemanlara doğru esnek ve dereceli bir geçiĢe izin verilir. Bant kopma noktasına
kadar esnetilmesine rağmen, halen dıĢarıda kalan noktalara (nesnelere) ise 0 üyelik
derecesi verilir. Bu durum ġekil 3.13 ve ġekil 3.14 „de gösterilmiĢtir.
ġekil 3.13. Geleneksel küme durumu (Eroğlu, 2006)
ġekil 3.14. Bulanık küme durumu (Eroğlu, 2006)
Bulanık bir küme, sınır koĢulları esnek olarak tanımlanan bir kümedir. Bulanık
küme teorisi, kısmi üyeliğe izin vererek geleneksel küme teorisini genelleĢtirir ve küme
üyeliği için [0,1] aralığındaki herhangi bir değeri kabul eder. Bulanık bir küme, evrensel
kümedeki her bir elemanın [0,1] aralığındaki bir sayı ile eĢlendiği,
μ A (x) → [0,1]
52
biçimindeki üyelik fonksiyonu olarak tanımlanır. Bulanık kümelerde bir nesnenin
üyelik derecesi, 0 ve 1 arasındaki bir sayı ile açıklanır. Burada, 0 sayısı ilgili nesnenin
kümeye ait olmadığını, 1 sayısı ilgili nesnenin kümenin tam üyesi olduğunu ve bu iki
değer arasındaki herhangi bir sayı ise ilgili nesnenin kümeye üyelik derecesini veya
kısmi üyeliğini gösterir. Buna göre, bulanık küme teorisinde kümenin elemanı olmayan
nesnelerden, kümenin tam elemanı olan nesnelere doğru esnek ve dereceli bir geçiĢe
izin verilir (Eroğlu, 2006).
Bulanık küme, bir nesne ve bu nesnenin ilgili kümeye üyelik derecesini
gösteren,
x,μ A (x)
A
x X
(3.20)
Ģeklindeki sıralı çiftlerle ifade edilir. Burada her bir (x, μ A (x)) çiftine bulanık teklik
denir. Bir bulanık teklik, μ A (x) / x olarak da tanımlanabilir. Eğer X kümesi,
{x , x
1
2
,..., x n } Ģeklinde kesikli bir küme ise; bir bulanık A kümesi,
A = μ A (x1 ) / x1 + ... + μ A (x n ) / x n
(3.21)
Ģeklinde gösterilir. Eğer X kesikli olmayan bir küme ise; A bulanık kümesi,
μ A (x i ) / x i
A
x
olarak ifade edilir.
A bulanık kümesi için verilen ifadelerde
,
, / ve + iĢaretleri cebirsel
anlamda sırasıyla toplam, integral alma, bölme ve toplama iĢlemlerini göstermez.
ve
iĢaretleri bulanık tekliklerin sırasıyla kesikli ve sürekli evrenlerde bir araya
getirilmesini ifade eder. / simgesi, matematiksel olarak
(x, μ A (x))
tekliğini ifade
etmek için kullanılan bir ayraçtır. + iĢareti ise, bulanık tekliklerin birleĢimini gösteren
bir simgedir (Eroğlu, 2006).
Bulanık küme ile ilgili baĢlıca tanımlar Ģunlardır:
53
1. Destek kümesi;
Bulanık bir kümenin üyelik fonksiyonunda, üyelik derecesi sıfırdan büyük olan
elemanların bir araya getirildiği kümeye destek kümesi denir ve aĢağıdaki Ģekilde
tanımlanır (Eroğlu, 2006);
Destek(A)
x
X, μ A (x)
0
2. α – Kesmesi;
Bulanık bir kümenin
kesmesi, üyelik fonksiyon değeri
' ya eĢit veya daha
büyük olan elemanların yer aldığı geleneksel olan elemanların yer aldığı geleneksel
(bulanık olmayan) bir kümedir. Seçilen her bir α değeri ile farklı bir
oluĢturulur.
değeri,
kesme kümesi
(0,1] koĢuluyla tanımlanan gerçel bir sayıdır. Her bir
düzeyi ile üyelik fonksiyonunun farklı bir dilimi belirlenir.
kesme kümesi
matematiksel olarak (Eroğlu, 2006);
Aα
x
X;μ A (x)
α
ve α (0,1]
biçiminde tanımlanır.
3. Dışbükeylik kavramı;
x1 ,x 2
X ve λ [0,1]
ile
μ A (λx1 (1- λx 2 )) min(μ A (x1 ),μ A (x 2 ))
koĢulunu sağlayan üyelik fonksiyonu dıĢbükeydir (Eroğlu, 2006).
4. Bulanık sayılar;
Bulanık sayılar, bulanık kümelerin özel bir alt kümesidir. Bulanık kümelerde
geçerli olan birleĢim, kesiĢim,
kesimi, geniĢleme kuralı gibi küme teorik iĢlemler
bulanık sayılara da kolayca uygulanabilir. Bulanık sayıların tanımlı olduğu evrensel
küme, gerçel sayılar kümesi, tamsayılar kümesi veya doğal sayılar kümesidir. Her
bulanık sayı bulanık bir küme olmasına rağmen, her bulanık küme bulanık bir sayı
değildir. Bulanık bir kümenin bulanık bir sayı olabilmesi için,
i.
Bulanık küme, normal bir bulanık küme olmalıdır.
ii.
Bulanık küme, dıĢbükey bir bulanık küme olmalıdır.
iii.
Bulanık kümenin destek kümesi sınırlı olmalıdır.
54
iv.
Bulanık kümenin her bir
kesmesi, gerçel sayı doğrusunun kapalı bir
aralığında tanımlı olmalıdır.
biçiminde tanımlanan özellikleri sağlaması gerekmektedir. Bulanık sayıların özel türü
olan üçgensel, yamuksal ve aralık bulanık sayılar uygulamada sıkça kullanılmaktadır
(Eroğlu, 2006).
5. Üçgensel bulanık sayı;
Üçgensel bulanık bir sayı
gibi üç parametre ile tanımlanır.
ve
;
üçgensel bulanık bir sayının alt ve üst sınır değerleri olmak üzere, üyelik derecesinin
sıfır olduğu noktaları vermektedir.
ise üyelik derecesinin bire eĢit olduğu noktayı
verir ve mod değeri olarak yorumlanır. Üçgensel bir bulanık sayı, ġekil 3.15„ de
gösterilmiĢtir.
ġekil 3.15. Üçgensel bulanık sayı (Eroğlu, 2006)
Üçgensel bir bulanık sayı;
0,
μ A (x;a1 ,a 2 ,a 3 )
x
a1
(x- a1 ) / (a 2 - a1 ), a1
x
a2
(a 3 - x) / (a 3 - a 2 ), a 2
x
a3
0,
x
a3
biçimindeki üyelik fonksiyonu ile ifade edilir (Eroğlu, 2006).
55
6. Kesişim işlemi;
Standart bulanık kesiĢim iĢleminde iki tane bulanık alt kümenin kesiĢimi
durumunda her bir kümeye ait öğenin ait oldukları kümelerdeki üyelik derecelerinin en
küçüğü alınır. Matematiksel olarak;
μ (A
B)
(x)
min(μ A (x),μ B (x)), x
X
μ A (x) μ B (x)
biçiminde gösterilir. μ (A
B)
(x) üyelik derecesi, A ve B bulanık kümelerinin her ikisinde
birden x elemanının bulunma derecesini belirler. Burada “ ”, “ve” anlamındadır
(Eroğlu, 2006).
7. Birleşim işlemi;
Ġki tane bulanık alt kümenin birleĢimi durumunda her bir kümeye ait öğenin ait
oldukları kümelerdeki üyelik derecelerinin en büyüğü alınır. Matematiksel olarak;
μ (A
B)
(x)
max(μ A (x),μ B (x))
μ A (x) μ B (x)
biçiminde gösterilir. μ (A
B)
(x) üyelik derecesi, bir x elemanının A veya B bulanık
kümesine ait olma derecesini belirlemektedir. Burada “
”, “veya” anlamındadır
(Eroğlu, 2006).
8. Tümleme;
A ve B bulanık kümeleri için aĢağıdaki Ģart sağlanıyor ise, A ve B için
C
C
tümleyendir denir ve B = A ve A = B ile gösterilir (Paksoy, 2002).
μ A (x) 1- μ B (x), x U
U: Evrensel küme
9. Geçiş noktası;
A bulanık kümesinin geçiĢ noktaları, üyelik derecesi 0,5 olan U evrensel
kümesinin elemanlarıdır (Paksoy, 2002).
56
3.8.3.2. Bulanık ortamda karar verme
Amaç fonksiyonları veya kısıtlar için kesin değerler yerine, sınırları kesin olarak
belirlenmemiĢ seçeneklerin söz konusu olduğu “civarında”, “etrafında” terimleri
kullanılabilir. Bu ifadelerin yer aldığı bulanık amaçlar ve kısıtlar, bulanık kümeler
kullanılarak, seçenekler arasından kesin olarak tanımlanabilir. Bu durum göz önüne
alındığında bulanık bir karar, bulanık amaçların ve bulanık kısıtların kesiĢimi
sonucunda elde edilen bulanık alternatifler kümesidir. Dolayısıyla bulanık bir karar,
amaçlar ve bazı kısıtlar bulanıksa elde edilebilir. Bulanık ortamda kısıtlar ve amaç
fonksiyonları arasındaki iliĢki tamamen simetriktir, yani iliĢki arasında bir fark yoktur
(Zimmermann, 1991).
Bulanık hedefler ve bulanık kısıtlar verildiğinde, amaçlar ve kısıtların kesiĢimi
olarak, bulanık bir çevrede karar verme problemi tanımlanabilir. Özellikle, X
alternatiflerin kümesi verildiğinde, bulanık karar D bir bulanık küme seti olarak
tanımlanır. Kümelerin kesiĢimi ise D G
C Ģekliyle gösterilir. Bulanık küme D‟ nin
ilgili üyelik fonksiyonu Ģu Ģekilde verilmiĢtir.
μ D (x) = Min (μ G (x), μ C (x))
(3.22)
Daha genel olarak n tane amaç G1 ,..., G n , m tane kısıt C1 ,..., C m varsa, karar D
bir bulanık küme olarak Ģu Ģekilde belirtilebilir;
D G1
G 2 ... G n
C1... Cm
(3.23)
Min μ G1 (x),...,μ G n (x),μ C1 (x),...,μ Cm (x)
(3.24)
Üyelik fonksiyonu eklenirse;
μ D (x)
biçiminde tanımlanır (Ramaswamy, 1998).
3.8.3.3. Bulanık doğrusal programlama
Doğrusal programlama, değiĢkenlere ve kısıtlayıcılara bağlı kalarak amaç
fonksiyonunu en uygun (maksimum veya minimum) kılmaya çalıĢır. Buna göre
57
doğrusal programlama, değiĢkenlere ve kısıtlayıcılara bağlı kalarak amaca en iyi ulaĢma
tekniğidir. Temelde doğrusal programlama, verilen optimallik ölçütüne bağlı kalarak kıt
kaynakların optimal olarak dağıtımını içeren matematiksel bir tekniktir (Öztürk, 1997).
DP problemleri ile ilgili bazı temel kavramlar aĢağıdaki gibi tanımlanabilir:
DeğiĢken: Problemde değiĢim gösteren faktörlerdir.
Karar (kontrol) değiĢkeni: Karar verici denetimi altında olan değiĢkenlerdir. DP
kullanılarak amaç fonksiyonunu en iyileyen karar değiĢkeni değerleri saptanır.
Amaç fonksiyonu: Karar değiĢkenlerinin matematiksel fonksiyonudur ve sistemi
tanımlamak için kullanılır. Karar vericinin isteklerini ifade etmek için kullanılır.
Alacağı değer önceden belirlenemez.
Kısıt: Karar değiĢkenlerinin matematiksel fonksiyonudur ve sistemi tanımlamak
için kullanılır. Karar vericinin elindeki olanakları ifade eden ve karar vericiyi belli
koĢullar altında karar vermeye yönelten matematiksel fonksiyonlardır. Bulunan
çözümler mutlaka problemin kısıtlarını sağlamalıdır (Pelitli, 2007).
n tane değiĢken ve m tane eĢitlik ya da eĢitsizlik Ģeklinde kısıt içeren bir DP
problemi, matematiksel olarak genellikle aĢağıdaki gibi formüle edilir:
Amaç fonksiyonu:
max(min)Z(x) c1x1 +c2 x 2 +...+cn x n
Kısıtlar:
a11x1 +a12 x 2 +...+a1n x n
, ,
b1
a 21x1 +a 22 x 2 +...+a 2n x n
, ,
b2
a m1x1 +a m2 x 2 +...+a mn x n
xj
Ģeklindedir.
0
, ,
bm
(3.25)
58
Problem kısaca;
n
max(min)Z(x)
c jx j
j =1
n
a ij x j
, ,
bi , i=1,...,m
(3.26)
j 1
xj
0, j=1,...,n
biçiminde de formüle edilebilir. Burada;
: Karar vericinin denetimi altında olan ve bilinmeyeni gösteren karar
xj
değiĢkenlerini,
Z(x) : En iyilenecek amaç fonksiyonunu,
cj
:
j. karar değiĢkeninin amaç fonksiyonundaki katkı katsayısını,
a ij
:
j. karar değiĢkeninin i. kısıttaki katkı katsayısını (teknolojik katsayıları),
bi
:
i. sınırlı kaynak miktarını yani i. kısıtın sağ yan değerini göstermektedir.
Bulanık doğrusal programla (BDP) problemleri temelinde doğrusal programlama
(DP) problemlerinden çıkmıĢtır. DP‟ de kısıtlara bağlı kalınmak koĢuluyla amaç
fonksiyonu en büyüklenmeye (en küçüklenmeye) çalıĢılmaktadır. Ancak gerçek
problemlerde amaç fonksiyonu ve kısıtlayıcıların bu kadar kesin ifade edilemeyeceği
aĢikârdır. Bu sebepten amaç fonksiyonlarını eniyilemek yerine belirli bir tatmin
derecesinde problemi ele almanın daha uygun olacağı düĢünülmektedir (Türe, 2006).
Eğer herhangi bir model söz konusu probleme herhangi bir sınırlama olmaksızın
yaklaĢıyorsa modelin daha da karmaĢıklaĢtığı, bir çözüm bulmanın zorlaĢtığı ve
birbirleriyle çeliĢkili sonuçlar elde etmenin doğal olduğu söylenir. Ayrıca gerçek
problemler, günlük dilde ifade edilen kısıt ve amaçlar içerir. Bunlar “A lira civarında
kazanmak istiyoruz” ya da “yatırımları B lira civarında ya da daha az miktarda tutmak
istiyoruz” gibi ifadelerdir. Bu tür belirsizliği bulanık küme terimleriyle ifade eden
bulanık matematiksel programlama, basit ve çok kullanıĢlı bir yöntemdir (Pelitli, 2007).
BDP, bulanık mantık ve DP‟nin bir birleĢimidir. Yani BDP, DP yöntemi
kullanılarak çözümlenebilen problemlere birçok karar sürecinde görülen belirsizlik
dâhil edildiğinde kullanılan bir yöntemdir. Günümüzde, birçok karar sürecinin belirsiz
59
bir yapıya sahip olduğu düĢünülürse BDP‟ nin DP‟den daha etkin ve kullanıĢlı bir
yöntem olduğu sonucuna varılabilir (Pelitli, 2007).
3.8.3.4. Bulanık doğrusal programlama ile doğrusal programlama yönteminin
karĢılaĢtırılması
Doğrusal programlama (DP) problemlerinde kesin sayılarla çalıĢılır ve bir
belirlilik söz konusudur. Hâlbuki pratikte modeli oluĢturan parametrelere iliĢkin net
değerlere ulaĢmak çoğu zaman mümkün olmamaktadır. Bu belirsizlik durumu, Zadeh
tarafından 1965 yılında önerilen “bulanık küme teorisi” ile dilsel olarak “az çok”,
“biraz” gibi formlarda ifade edilebilir hale gelmiĢtir. Kesin olmayan bilginin sayısal
gösterimi olan bulanık sayıların kullanılması ile gerçek dünya problemlerinin belirsiz
yapısının modellenmesinde kullanılacak yeni matematiksel teknikler geliĢtirilmiĢtir. Bu
belirsizlik içinde geliĢtirilen yöntemler, doğrusal programlamadan hayli farklıdır. Bazı
durumlarda, amaç fonksiyonu maksimizasyon veya minimizasyon yerine, “maliyetin
önemli ölçüde düĢürülmesi” gibi belirsiz bir hedef olabilmektedir. Bazen de, teknoloji
matrisinin elemanları veya sağ taraf sabitleri, tat, koku, ağrı gibi kesin tanımlanamayan
duyumları ya da nitel özellikleri yansıttıkları için doğal yapıları gereği bulanık bir
karakter taĢıyabilirler. Herhangi bir kısıttaki ihlalin mümkün olmayan çözüme sebebiyet
verdiği DP‟ den farklı olarak bulanık doğrusal programlamada, küçük ihlaller kabul
edilebilir. Tüm bu farklılıklardan anlaĢılacağı üzere, BDP, DP‟ nin daha geniĢletilmiĢ
bir halidir. BDP‟ de, DP‟ nin aksine tek tip bir model yoktur ve modellenecek sistemin
özelliklerine ve kabullerine bağlı olarak pek çok varyasyon mümkündür (Paksoy, 2002).
DP ve BPD yöntemlerinin karĢılaĢtırılması dört temel esasa göre yapılmaktadır.
Bunlar;
i. Varsayımları açısından: Bir problemin bu iki yöntemden herhangi biri
kullanılarak
çözülebilmesi
için
oransallık,
toplanabilirlik
ve
bölünebilirlik
varsayımlarının sağlanması gerekir. Ancak problemin DP ile çözülebilmesi için kesinlik
varsayımının sağlanması gerekirken, BDP ile çözülebilmesi için kesin olmama
varsayımının sağlanması gerekir. Gerçek hayatta karĢılaĢılan problemlerin çoğunlukla
kesin olmama varsayımını sağladığı düĢünülürse BDP‟nin DP‟ye üstün olduğu
söylenebilir. Yine bir problemin söz konusu iki yöntemden biri kullanılarak
60
çözülebilmesi için karar değiĢkenleri arasında alternatif seçim olanağı olmalı ve
kaynaklar kısıtlı olmalıdır (Pelitli, 2007).
ii. Formülasyonları açısından: Formülasyonda yer alan değiĢken, karar
değiĢkeni, amaç fonksiyonu ve kısıt gibi temel kavramların tanımı her iki yöntem için
de aynıdır. DP ile BDP problemlerinin formülasyonları arasındaki farklılık
yerine
(yaklaĢık olarak daha küçük ya da eĢit), = yerine
yerine
~
(yaklaĢık eĢit),
(yaklaĢık olarak daha büyük ya da eĢit) ve örneğin c1 yerine
kullanılmasından
kaynaklanmaktadır.
“~”
simgesi
~
~
~c gösteriminin
1
bulanıklaĢtırıcı
olarak
adlandırılmakta ve incelenmekte olan problemdeki bulanık öğeleri göstermek için
kullanılmaktadır. Bu gibi gösterimler içeren eĢitlik ya da eĢitsizlik Ģeklindeki kısıtlar
bulanık eĢitlik ya da bulanık eĢitsizlik olarak adlandırılır. ~c gibi gösterimler ise
1
bulanık sayı olarak adlandırılır (Pelitli, 2007).
iii. Amaçları açısından: DP‟ de amaç, problemin optimal uygun çözümüne
ulaĢmaktır. BDP‟ de ise amaç, en yüksek üyelik derecesine sahip bulanık karar olarak
tanımlanan optimal karara ulaĢmaktır. Amaç fonksiyonunu en iyilemektense amaç
fonksiyonunu belirli bir tatmin derecesi ile ele alan bir yaklaĢımı benimsemenin gerçek
problemleri incelemek için daha uygun bir yaklaĢım olduğu söylenmektedir (Pelitli,
2007).
iv. Yapıları açısından: DP‟de amaç fonksiyonu, problemin formülasyon ve
çözüm aĢamasında gereklidir. Oysa BDP‟ de herhangi bir amaç fonksiyonunun olması
gerekli değildir. Problemin formülasyonu aĢamasında herhangi bir amaç fonksiyonu
mevcut olsa bile, çözüm aĢamasında bu fonksiyon kısıta dönüĢtürülür (Pelitli, 2007).
3.8.3.5. Bulanık doğrusal programlama problemlerine çözüm yaklaĢımları
Literatürde bulanık doğrusal programlama modeliyle ilgili birçok yaklaĢım
bulunmaktadır. Bunların baĢında Zimmermann, Werners ve Verdegay yaklaĢımları
gelmektedir.
61
i.
Zimmermann yaklaĢımı:
Zimmermann, bulanık amaç ve bulanık kısıtlayıcılı DP problemleri için simetrik
bir yaklaĢım önermiĢtir. Zimmermann‟ a göre bulanık amaç fonksiyonu, karar vericiden
sağlanan bulanık bir eriĢim düzeyi ile bulanık bir kısıtlayıcı olarak ifade edilebilir. Bu
durumda, bulanık karar kümesi belirlenirken bulanık amaç ve bulanık kısıtlayıcılar
birbirlerinden farksız olarak ele alınır. Zimmermann (1983), karar vericinin ulaĢmak
istediği amaç fonksiyonunun değeri için bir Z istek seviyesinin (aspiration level),
kurulabileceğini ve kısıtların her birinin bir bulanık küme olarak modellenebileceğini
öne sürmüĢtür (Pelitli, 2007).
Bu yaklaĢımda bulanık amaç fonksiyonunun b 0 amacı ve p 0 hoĢgörü miktarı ile
tüm bulanık kaynakların bi ve pi değerleri önceden verilir. Bulanık amaçlar ve bulanık
kısıtların birbirilerinden farksız oldukları düĢünülür ve
i için b i ,b i
pi
aralıklarıyla
tanımlanır. Dolayısıyla,
~
ma x Z cT x
(Ax)i
x
bi
(3.27)
i=1,2,....m
0
eĢitliği, x‟ in bulunması problemine dönüĢür.
cT x b 0
(Ax)i bi
x
i 1, 2,
,m
(3.28)
0
Burada ≤ iĢareti ≤ iĢaretinin bulanıklaĢtırılmıĢ halidir. ≤ iĢareti, “ (Ax) i
~
~
kısıtlayıcısı bi civarında veya daha azdır” Ģeklinde yorumlanır. Benzer olarak ≥ iĢareti
~
de ≥ iĢaretinin bulanıklaĢtırılmıĢ halidir. ≥ iĢareti, “ c T x amacı b 0 civarında veya daha
~
fazladır” Ģeklinde yorumlanır. Bulanık amaç fonksiyonunun her iki tarafı da (-1) ile
çarpılırsa BDP problemi aĢağıda verildiği gibi tamamen simetrik olarak,
62
- cT x - b 0
(Ax)i bi
x
i 1, 2,
,m
(3.29)
0
Ģeklinde ifade edilebilir.
Burada B=
- cT
Ai
ve d=
- b0
bi
sütun vektörleri tanımlanırsa BDP problemi aĢağıda
verildiği gibi düzenlenebilir.
Bx
d
x 0
pi ‟ ler amaç fonksiyonu ve kısıtlayıcılardaki kabul edilebilir toleransları gösteren ve
karar verici tarafından belirlenen sabitlerdir. Bu durumda, i. bulanık eĢitsizliğin üyelik
fonksiyonu matematiksel olarak aĢağıdaki gibi ifade edilir.
0 ,
μi
Bx
i
=
[0,1] ,
1,
(Bx)i
di
d i + pi
(Bx)i
(Bx)i
di
ise
d i + pi
ise
(3.30)
ise
Buradan hareketle, bulanık amaç fonksiyonu ve bulanık kısıtlayıcıların parçalı
doğrusal üyelik fonksiyonları sırasıyla aĢağıda verildiği gibi tanımlanır:
0 ,
μ0 x = 1 -
b0 - cT x
,
p0
1 ,
cT x
b0 - p0
b0 - p0
cT x
cT x
b0
ise
b 0 ise
ise
(3.31)
63
0 ,
μi x = 1 -
Ax i >bi + pi
(Ax)i - bi
,
pi
1 ,
bi
Ax
i
Ax i < bi
Burada, örneğin μ 0 x
ise
bi + pi ise
(3.32)
ise
üyelik fonksiyonu, çözüm vektörü x‟ in bulanık
eĢitsizlik cT x b0 ‟ i doyurma derecesi olarak yorumlanır.
Bulanık amaç ve bulanık kısıtlayıcıların üyelik fonksiyonları belirlendiği için
bulanık karar kümesi,
μ
x
D
min μ 0 (x),μ i (x)
i=1,2,…,m
(3.33)
eĢitliğinden oluĢturulabilir. Bulanık karar kümesinin en yüksek üyelik dereceli elemanı
ise,
μ
x
D
max min μ 0 (x),μ i (x)
(3.34)
x 0
eĢitliğinden belirlenir.
Bulanık amaç ve bulanık kısıtlayıcılar için tolerans betimlemesi kullanıldığı
zaman, bir maksimizasyon kararı olan μ (x ) , klasik bir DP modelinin kurulması ile
D
belirlenebilir. Diğer bir ifadeyle, simetrik BDP problemleri, ek bir değiĢken olan ‟nın
kullanılması ile klasik bir DP modeli olarak ifade edilebilir. Dolayısıyla, bulanık karar
kümesi için,
min[μ0 (x),μi (x)] μ0 (x) μi (x)
(3.35)
i
ifadesi yazılabilir. Burada
değiĢkeni bulanık amaç ve bulanık kısıtlayıcıların çözüm
vektörü x tarafından eĢ zamanlı olarak doyurulma derecesini gösterir.
değiĢkeni,
[0,1] aralığında tanımlanır. Buradan μ (x ) ‟ ı belirleme problemi klasik bir DP
D
problemi olarak aĢağıda verildiği gibi ifade edilir.
64
max
μ 0 (x)
(3.36)
μ i (x)
[0,1]
Bulanık amaç ve bulanık kısıtlayıcıların üyelik fonksiyonları yukarıdaki
modelde yerine konduğu zaman aĢağıda verilen DP modeline ulaĢılır:
max
b0 - cT x
1p0
1-
(Ax)i - bi
pi
; i
(3.37)
[0,1]
x 0
Bu model, cT x ve (Ax)i terimlerine göre düzenlendiği zaman,
max
cT x
b0 - (1- )p0
v(Ax)i
bi (1- )pi ; i
(3.38)
[0,1]
x 0
olarak ifade edilir. Burada c j , a ij , b0 , p0 , bi ve pi ‟ lerin problemin çözümünden önce,
karar verici tarafından belirlenmesi gerekmektedir. Yukarıda verilen DP probleminin
klasik bir DP problemi olduğu açıktır.
=1- θ olduğunda eĢitlik,
min θ
cT x
(Ax)i
b 0 - θp0
bi + θpi ; i
θ [0,1]
x 0
„ye denktir.
(3.39)
65
c, A, b0 , p0 , bi ve pi ,
i verilir ve θ , maksimum toleransın bir parçasıdır. Bu eĢitliğin
optimal çözümü tektir.
Bulanık amaç ve bulanık kısıtlayıcılı DP problemlerinde bazı kısıtlayıcılar
bulanıklık içermeyebilir. Bu durumda, ilgili kısıtlayıcıların (Ex) maksimum toleransları
0 olarak kabul edilir. Diğer bir ifadeyle, bulanık olmayan kısıtlayıcılar herhangi bir
dönüĢüm iĢlemi yapılmadan,
max
cT x
b 0 - (1- )p 0
(Ax)i
bi + (1- )pi ; i
(Ex)i
bi
(3.40)
[0,1]
x 0
Ģeklinde (3.39) modeline ilave edilebilir (Pelitli, 2007).
ii.
Werners yaklaĢımı:
Zimmermann yaklaĢımından farklı olarak, Werners yaklaĢımında amaç
fonksiyonuna iliĢkin üyelik fonksiyonu, oluĢturulan modelin çözülmesiyle analist
tarafından belirlenir. Werners yaklaĢımında, kısıtlayıcıların üyelik fonksiyonları karar
verici tarafından belirlenebilmesine rağmen, kısıtlayıcıların bulanık olması nedeniyle,
bulanık olarak algılanan amaç fonksiyonuna iliĢkin üyelik fonksiyonu, karar verici
tarafından önceden belirlenemez. Werners, amaç fonksiyonuna iliĢkin üyelik
fonksiyonunu belirleyebilmek için Orlovski‟nin önerdiği bulanık karar kümesini temel
olarak almıĢtır. Orlovski, bulanık kısıtlayıcıların oluĢturduğu tanım kümesinin (veya
bulanık çözüm uzayının) her bir
kesim kümesi için, amaç fonksiyonunun optimal
değerlerini belirlemeyi ve bu optimal değerlerle eĢit üyelik dereceli olan çözüm
uzayının
kesim kümesini, bulanık karar kümesi olarak ele almayı önermiĢtir (Pelitli,
2007).
maxZ cT x
(Ax)i
x
0
bi , i
(3.41)
66
Werners (1987), eĢitlik Zimmermann‟ ın modelinin sağ yan değerleri bulanık
olduğu için amaç fonksiyonunun da bulanık olması görüĢündedir. Yani,
ma x Z cT x
(Ax)i
x
(3.42)
bi , i
0
Bu eĢitlik aĢağıdaki modele eĢittir;
ma x Z cT x
bi + θpi
(Ax)i
(3.43)
θ [0,1]
x
0
c, A, bi ve pi verilmiĢ fakat bulanık amacın hedefi verilmemiĢtir. Werners yaklaĢımını
kullanarak bu problemi çözmek için Z0 ve Z1 değerlerinin belirlemek gerekir.
Zimmermann algoritmasında olduğu gibi p0 ve b0 değerlerini karar vericiye sorarak
üyelik fonksiyonu oluĢturmak yerine, karar vericinin bu değerleri veremeyeceğini
düĢünerek iki olası uç nokta olan Z0 ve Z1 değerlerini kullanmaktadır. Bu değerler
aĢağıdaki gibidir;
Z0
min( max cT x)=Z
(θ=0)
Z1
max( max cT x)=Z
(θ=1)
X
x (Ax)i
x X
x X
bi θpi ,
i, θ [0,1] ve x
(3.44)
0
Dolayısıyla Z0 ve Z1 değerlerini kullanarak amaç fonksiyonu için sürekli artan
doğrusal bir üyelik fonksiyonu oluĢturulabilir. Optimal çözüm, Z0 ve Z1 arasında bir
değer alacağı için optimal çözümün değeri arttıkça memnuniyette artacaktır.
Bu durumda amaç fonksiyonunun ve bulanık kısıtların üyelik fonksiyonu
aĢağıdaki gibidir:
67
cT x
0 ,
μ0 x = 1 -
Z1 - cT x
,
Z1 - Z0
Z0
0 ,
ise
cT x
cT x
1 ,
μi x = 1 -
Z0
Z1
Z1 ise
ise
Ax i >bi + pi
(Ax)i - bi
,
pi
bi
1 ,
(3.45)
Ax
Ax i < bi
ise
i
bi + pi ise
(3.46)
ise
Optimal karara ulaĢmak için Bellman ve Zadeh tarafından önerilen min iĢlemcisi
kullanarak, μ D üyelik fonksiyonu ile belirlenen D karar alanı elde edilebilir:
μ D = min(μ0 ,μ1 ,...,μ m )
(3.47)
μ D ‟ nin eĢitlik (3.41)‟ nin optimal çözüm olarak maksimum olduğu kararı seçmek
uygundur. Bu nedenle eĢitlik (3.41),
max
μ0
μi
(3.48)
, μ 0 ve μ i
x
[0,1] , i
0
„ye eĢittir. Burada c,A,bi ,pi ,
i
verilir ve λ= μ D = min(μ0 ,μ1 ,...,μ m ) ‟ dir. Bu eĢitlik
gerçekte Zimmermann tarafından sunulan modele benzeyen simetrik bir modeldir. Ġki
model arasındaki farklılık üyelik fonksiyonlarının biçimlerinden kaynaklanmaktadır.
=1- θ olduğunda problem,
min θ
cT x Z1 - θ(Z1 - Z0 )
(Ax)i bi + θpi ; i
θ [0,1]
x 0
(3.49)
68
eĢitliğine denk olacaktır. c, A, bi , pi , i verilir ve θ , ilk kısıt için (Z1 - Z0 ) ‟ ın bir
parçası ve diğerleri için maksimum toleransın bir parçasıdır. Çözüm tek bir optimal
çözümdür (Pelitli, 2007).
iii.
Verdegay yaklaĢımı:
Zimmermann ve Werners‟ tan farklı olarak, Verdegay, bulanık kısıtlayıcılı bir
DP probleminin çözümünün bulanık bir küme ile temsil edilmesi gerektiğini öne
sürmüĢtür. Verdegay bu düĢünceden hareketle bulanık kısıtlayıcılı bir DP problemi
modelinin çözümünü betimleme teoremi ve parametrik programlamayı kullanarak
belirlemeye çalıĢmıĢtır. Betimleme teoremi, bulanık bir kümenin
kesim kümelerine
göre ifade edilebilmesine olanak tanır. Verdegay‟ a göre, söz konusu modelin optimal
çözümünün bulunması için bulanık kısıtlayıcı kümesinin α [0,1] koĢuluyla
kesim
kümelerinin belirlenmesi gerekir. Bulanık kısıtlayıcıların μ i (x) ile gösterilen üyelik
fonksiyonlarının sürekli ve monotonik bir Ģekilde tanımlanması halinde kısıtlayıcı
kümesinin
Xα
kesim kümeleri aĢağıdaki Ģekilde bulunur (Pelitli, 2007).
x μi (x)
, i, x
0
[0,1]
(3.50)
Bu durumda, bulanık kısıtlayıcılı DP probleminin çözümü,
maxZ cT x
x Xa
(3.51)
[0,1]
veya
maxZ cT x
μ i (x)
x
[0,1]
0
probleminin çözülmesiyle belirlenir.
(3.52)
69
Bulanık kısıtlayıcıların üyelik fonksiyonları:
0 ,
μi x = 1 -
Ax i >bi + pi
(Ax)i - bi
,
pi
1 ,
bi
Ax
i
Ax i < bi
ise
bi + pi ise
(3.53)
ise
olduğundan eĢitsizlik,
maxZ cT x
(Ax)i - bi
1pi
(3.54)
[0,1]
x
0
veya
maxZ cT x
(Ax)i
bi (1- )pi
(3.55)
[0,1]
x
0
olarak elde edilir alır.
Burada θ 1
olarak kabul edilirse aĢağıda verilen parametrik programlama
problemine ulaĢılır. Elde edilen bu parametrik çözümde θ = 0 için α = 1 ‟ dir. θ,[0,1]
aralığında hareket ederken, memnuniyet derecesi %100‟ den %0‟ a doğru iner. θ = 0
sapma sıfır düzeyindedir ve memnuniyet derecesi 1 tam değerini alır. θ = 1 en yüksek
toleransı gösterir ve Z , maksimizasyon probleminde en yüksek değerini alır (Paksoy,
2002).
MaxZ cT x
(Ax)i
bi + θpi
θ [0,1]
x
0
(3.56)
70
Seçilen her bir θ değeri için bu problemin farklı bir optimal çözümü bulunur.
θ [0,1] koĢuluyla belirlenen θ değerine göre yukarıda verilen problemin çözülmesi,
bulanık karar kümesinin bir elemanının belirlenmesi anlamına gelir.
3.8.3.6. Konno -Yamazaki modeline bulanık doğrusal programlama yaklaĢımı
Konno - Yamazaki portföy seçim modeli, karar vericilere farklı getiri ve risk
kombinasyonlarında nasıl bir portföy oluĢturulması gerektiği hakkında bir bilgi
vermemektedir. Ayrıca, riske karĢı kayıtsız yatırımcılar riskle pek ilgilenmezler ve
yatırım kararlarını sadece beklenen getiriye göre alırlar. Riske karĢı kayıtsız yatırımlar
için farklı getiri seviyelerinde optimal çözümler elde etmek için Konno-Yamazaki
portföy modeli çözülerek de sonuca gidebilir. Ancak, riskten kaçan ve riski seven
yatırımcılar için risk ve getiri arasında bir tercih söz konusudur. Örneğin, beklenen
getiri oranındaki artıma bağlı olarak katlanılabilecek risk düzeyinden daha yüksek bir
risk alınabilir veya çok düĢük bir riskle makul bir getiri beklenebilir. Görüldüğü gibi
getiri ve risk faktörleri, yatırımcılar tarafından kesin ve doğru bir Ģekilde
değerlendirilemez. EĢitlik (3.19)‟ daki Konno-Yamazaki DP modelinin, 3. eĢitsizlik
kısıtının sağ taraf sabiti olan beklenen getiri oranının ( ρ ) bulanık olduğunu göz önüne
alırsak, Konno-Yamazaki doğrusal programlama modeli, bulanık kaynaklı doğrusal
programlama modeline dönüĢür (Pelitli, 2007). Beklenen getirinin artması yatırımcıların
memnuniyetini arttıracağından, 3. kısıtın üyelik fonksiyonu ġekil 3.16‟ da görüldüğü
gibi parçalı lineer monoton artan bir fonksiyon olarak tasarlanabilir (Kocadağlı, 2006):
n
0
,
ρM 0
rj x j
j=1
n
μ K (x)
rj x j ρM 0 / τ,
ρM 0
j=1
rj x j
ρM 0 + τ
j=1
n
1
n
,
rj x j
ρM 0 + τ
j=1
Burada τ , beklenen getirinin tolerans değeridir.
(3.57)
71
ġekil 3.16. Getirinin üyelik fonksiyonu (Kocadağlı, 2006)
Böylece bulanık kaynaklı Konno-Yamazaki doğrusal programlama modeli aĢağıdaki
gibi gösterilebilir:
T
Amaç Fonksiyonu:
MinZ
yt / T
(3.58)
t =1
n
Kısıt 1:
yt
a tj x j
0
t =1,2,...,T
a tj x j
0
t =1,2,...,T
j =1
n
Kısıt 2:
yt
j =1
n
Kısıt 3:
rj x j
ρ M0
j =1
n
Kısıt 4:
x j = M0
j =1
0
xj
yt
0
uj
j =1,2,...,n
t =1,2,...,T
Burada ρ M 0 (bulanık beklenen getiri miktarı), τ beklenen getirinin önceden
bilinen tolerans değeri [ρM0 , ρM0
τ] kapalı aralığındadır. ρM0 τ , beklenen getirinin
üst sınırı olarak karar verici tarafından belirlenir. Verdegay‟ a göre bulanık kaynaklı DP
modelleri aĢağıdaki modele denktir (Kocadağlı, 2006):
Min Z
x X
Burada X , α [0,1] olmak üzere
kesim kümesidir:
72
X
α,x
x i,μ i
0
Beklenen getirinin üyelik fonksiyonu Verdegay‟ ın modelinde yerine konursa,
μK
α
n
rj x j ρM 0 ] / τ α
[
j =1
n
rj x j ρM 0 ] τα
[
(3.59)
j =1
n
rj x j
ρM 0
τα
j =1
olmak üzere bulanık kaynaklı DP modeli,
T
Amaç Fonksiyonu: MinZ
(3.60)
yt / T
t =1
n
Kısıt 1:
yt
a tj x j
0
t =1,2,...,T
a tj x j
0
t =1,2,...,T
j =1
n
Kısıt 2:
yt
j =1
n
Kısıt 3:
α [0,1]
ρM 0 ατ
rj x j
j =1
n
Kısıt 4:
xj
M0
j =1
0
xj
yt
0
uj
j =1,2,...,n
t =1,2,...,T
parametrik DP problemine dönüĢür. Bu model α [0,1] olmak üzere beklenen getirinin
farklı
memnuniyet seviyelerine göre çözülerek belirli bir
memnuniyet seviyesinde
hangi hisse senetlerine ne kadar oranda yatırım yapılması gerektiği bulunabilir. Ayrıca,
karar vericiler, bu aĢamada belirli bir
seviyesine karĢılık gelen, hedef getiri ve risk
değerlerini belirleyebilirler. Ancak esas amaç, çeĢitli getiri ve risk kombinasyonları
arasından bir optimum çözüme ulaĢmak olduğundan bu model tam olarak yeterli
değildir. Werners, bulanık kaynaklar ve bulanık eĢitsizlik kısıtlarından dolayı amaç
73
fonksiyonunun da bulanık olabileceğini ileri sürmüĢtür. Verdegay‟ ın yaklaĢımında
olduğu gibi her bir bulanık kaynağın toleranslarının biliniyor olduğu varsayılmaktadır.
Werners‟ ın yaklaĢımının modele uygulanması için ilk olarak, yukarıdaki parametrik DP
modeli (3.60) sırasıyla, ρM0 (
0) ve ρM0 τ (
1) beklenen getirileri için
çözülerek Z0 ve Z1 (minimize edilen risk değerleri) amaç fonksiyonu değerleri
bulunur. Modeldeki beklenen getiri değeri arttırıldığında minimize edilen risk değeri de
artacağından Z1
Z0 ‟dır. Yatırımcılar riske karĢı duyarlı olduğundan risk arttığında
memnuniyet azalacaktır. Bunun için amacın üyelik fonksiyonu, Z0 ve Z1 değerlerinin
kullanılmasıyla parçalı doğrusal monoton azalan bir üyelik fonksiyonu,
Z Z0
1,
μ Z (x)
1 [Z Z0 ] / Z1 Z0 ,
Z0
0,
Z
Z Z1
(3.61)
Z1
biçiminde tasarlanabilir (Kocadağlı, 2006). Z değeri arttığında amaç fonksiyonun üyelik
derecesi (memnuniyeti) azalmaktadır. Beklenen getirinin üyelik fonksiyonu (μ K (x)) ve
amacın üyelik fonksiyonunun (μ 0 (x)) yardımıyla optimal bir çözüm elde etmek için
max-min operatörü kullanılabilir. ġöyle ki,
max x 0 α,α
min[μ Z (x),μ K (x)]
(3.62)
olmak üzere max-min operatörünün kullanılmasıyla problem çok amaçlı optimizasyon
problemine dönüĢür:
max min[μ Z (x),μ K (x)]
x 0
(3.63)
EĢitlik (3.61), aĢağıdaki probleme denktir.
Max.
μ Z (x)
μ K (x)
x 0
[0,1]
i = 1,2,...,m
(3.64)
74
Üyelik fonksiyonlarının, denklem (3.61)‟ de yerine konmasıyla, bulanık amaçlı
ve kaynaklı DP modeli, aĢağıdaki standart DP modeline dönüĢür:
Amaç fonksiyonu: Max. α
T
Kısıt 1:
(3.65)
y t / T α(Z1 Z0 )
Z1
t =1
n
Kısıt 2:
yt
a tj x j
0
t =1,2,...,T
a tj x j
0
t =1,2,...,T
j =1
n
Kısıt 3:
yt
j =1
n
Kısıt 4:
rj x j ατ ρM 0
α [0,1]
j =1
n
Kısıt 5:
xj
M0
j =1
0
xj
yt
0
j =1,2,...,n
uj
standart DP modeline dönüĢür. Bu modelin çözülmesiyle de, optimal bir α* değeri için
hangi hisse senetlerine ne kadar oranda yatırım yapılması gerektiği bulanabilir
(Kocadağlı, 2006).
Elde edilen modele Fiyat/Kazanç oranı ve Toplama-dağıtım endeksi kısıtları
eklenirse, geliĢtirilen model;
Amaç fonksiyonu: Max. α
Kısıt 1:
T
(3.66)
y t / T α(Z1 Z0 )
Z1
t =1
n
Kısıt 2:
yt
a tj x j
0
t =1,2,...,T
a tj x j
0
t =1,2,...,T
j =1
n
Kısıt 3:
yt
j =1
n
Kısıt 4:
j =1
rj x j ατ ρM 0
α [0,1]
75
n
Kısıt 5:
xj
M0
j =1
n
Kısıt 6:
x jFj
Fort
j =1
n
Kısıt 7:
x jA kj
Aj
k =1,2,3
j =1
0
xj
yt
0
uj
j =1,2,...,n
biçiminde oluĢturulur.
Burada;
T
: Ġncelenen dönem sayısı,
t
: T dönemi içindeki herhangi bir t. dönem,
ρ
: Beklenen getiri oranı,
rj
: j. hisse senedinin ortalama getiri oranı,
rj t : t dönemi boyunca j. hisse senedi için gerçekleĢen getiri oranı,
a tj : j. hisse senedinin riski ( rj t - rj ),
xj
: j. hisse senedine yapılan yatırımın payı,
uj
: j. hisse senedine yapılan yatırımın üst sınırı,
M0 : Toplam yatırım miktarı,
ρM0 : Beklenen getiri miktarı,
yt
: Yardımcı değiĢken,
Fj
: j. hisse senedinin son üç yıldaki F/K oranlarının ortalaması,
Fort : ĠMKB 30 endeksine dahil olan sektörlerin son üç yıldaki F/K oranlarının
ortalaması,
A j : j. hisse senedinin 36 aylık dönem boyunca ortalama ADI endeksi değeri,
A kj : j. hisse senedinin her yıl için ortalama ADI endeksi değeri.
76
4. ARAġTIRMA SONUÇLARI VE TARTIġMA
ÇalıĢmanın bu bölümünde, önerilen model yardımıyla ĠMKB 30 endeksine dahil
olan hisse senetleri için optimal bir portföy oluĢturulacak, elde edilen portföy için risk
ve getiri miktarları hesaplanacaktır. Daha sonra Vadeli ĠĢlem Opsiyon Borsası‟ nda
iĢlem gören ĠMKB 30 endeks sözleĢmesinin opsiyonlu alım durumu da sürece dahil
edilerek karĢılaĢtırmalı alternatif risk-getiri durumları incelenecektir.
4.1. Modelin Kurulması ve Çözülmesi
Çizelge 4.1. ĠMKB 30 endeksine dahil olan hisse senetleri
xj
Hisse senedi
xj
Hisse senedi
x1
AKBNK
x16
PETKM
x2
ARCLK
x17
SAHOL
x3
ASYAB
x18
SISE
x4
BIMAS
x19
SKBNK
x5
DOHOL
x 20
TAVHL
x6
DYHOL
x 21
TCELL
x7
ECILC
x 22
TEBNK
x8
ENKAI
x 23
THYAO
x9
EREGL
x 24
TKFEN
x10
GARAN
x 25
TOASO
x11
HALKB
x 26
TTKOM
x12
ISCTR
x 27
TUPRS
x13
KCHOL
x 28
VAKBN
x14
KOZAA
x 29
VESTL
x15
KRDMD
x 30
YKBNK
77
Çizelge 4.1‟ de ĠMKB 30 endeksine dahil olan hisse senetleri verilmiĢtir.
Modelin kurulabilmesi için öncelikle, hisse senetlerinin 36 aylık dönem boyunca aylık
olarak getirileri hesaplanmıĢtır (Bkz. EK-2).
Hisselerin aylık getirilerinin hesaplanması sonrasında beklenen getiri (hisse
senetlerinin ortalama getiri oranlarının ortalaması, ρ ) 0,02 (%2) ve hisse senetlerinden
elde edilebilecek maksimum beklenen getiri oranı da, hisse senetlerinin ortalama
getirilerinin maksimumu ( ρ max ) olarak 0,055 (%5,5) olarak bulunmuĢtur. Böylece
beklenen getirinin toleransı ( τ ρmax - ρ ) 0,035 (%3,5) dir. Beklenen getirinin üyelik
1 alınarak aĢağıdaki gibi oluĢturulmuĢtur.
fonksiyonu, M 0
n
0
,
ρM 0
rj x j
j=1
n
μ K (x)
rj x j ρM 0 / τ,
n
ρM 0
j=1
rj x j
ρM 0 + τ
j=1
n
1
,
ρM 0 + τ
rj x j
j=1
30
0
,
rj x j
0, 02
j=1
30
μ K (x)
rj x j 0,02 / 0, 035
30
, 0,02
j=1
rj x j
0,055
j=1
30
1
,
rj x j
0, 055
j=1
Burada τ , beklenen getirinin tolerans değeridir. Daha sonra aĢağıdaki
parametrik denklem, sırasıyla, ρM0 (
0) ve ρM0 τ (
1) beklenen getirileri için
çözülerek Z0 ve Z1 (minimize edilen risk değerleri) amaç fonksiyonu değerleri
bulunur.
T
Amaç Fonksiyonu: MinZ
yt / T
t =1
n
Kısıt 1:
yt
a tj x j
j =1
0
t =1,2,...,T
78
n
Kısıt 2:
yt
a tj x j
t =1,2,...,T
0
j =1
n
Kısıt 3:
rj x j
α [0,1]
ρM 0 ατ
j =1
n
Kısıt 4:
xj
M0
j =1
Bu modelin
0
xj
yt
0
j =1,2,...,n
uj
çözülmesi
t =1,2,...,T
ile
Z0
0,041
(%4,1) ve
Z1
0,119 (%11,9)
bulunmuĢtur. Z0 ve Z1 değerleri bulunduktan sonra amacın üyelik fonksiyonu,
iken Z0 ve
=0
= 1 iken Z1 değerlerinin kullanılmasıyla amacın üyelik fonksiyonu
aĢağıdaki biçimde elde edilir.
Z Z0
1,
μ Z (x)
1 [Z Z0 ] / Z1 Z0 ,
Z0
0,
Z
1,
μ Z (x)
Z Z1
Z1
Z 0, 041
1 [Z 0, 041]/ 0, 078
,
0,
0, 041 Z 0,119
Z 0,119
Üyelik fonksiyonlarının yerine konmasıyla, Toplama-dağıtım endeksi ve
Fiyat/Kazanç oranı kısıtlarının modele eklenmesiyle, bulanık amaçlı ve kaynaklı DP
modeli, standart DP modeline dönüĢür.
Amaç fonksiyonu: Max. α
Kısıt 1:
T
t =1
y t / T α(Z1 Z0 )
Z1
79
1/36(Y1+Y2+Y3+Y4+Y5+Y6+Y7+Y8+Y9+Y10+Y11+Y12+Y13+Y14+Y15+Y16+Y1
7+Y18+Y19+Y20+Y21+Y22+Y23+Y24+Y25+Y26+Y27+Y28+Y29+Y30+Y31+Y32+
Y33+Y34+Y35+Y36+0.078 α <=0.119
n
Kısıt 2:
yt
a tj x j
0
t =1,2,...,T
j =1
Y1+0.02X1+0.04X2+0.13X3+0.08X4+0.06X5-0.08X7-0.03X8+0.15X9+0.1X10+
0.02X12+0.07X13+0.14X14+0.22X15+0.04X17+0.1X18+0.04X19+0.08X210.06X22+0.14X23+0.08X25+0.01X27+0.04X28-0.06X29 +0.09X30>=0
………..
………..
………..
Y36+0.13X1+0.14X2+0.12X3+0.12X4+0.1X5+0.28X6+0.32X7+0.17X8+0.09X9+
0.19X10+0.28X11+0.2X12+0.16X13-0.04X14+0.18X15+0.11X16+0.06X17+ 0.22X18
+ 0.1X19 + 0.21X20+ 0.12X21+ 0.35X22+ 0.12X23+ 0.19X24+ 0.14X25+ 0.03X26+
0.12X27+ 0.34X28+0.19X29+0.1X30>=0
n
Kısıt 3:
yt
a tj x j
0
t =1,2,...,T
j =1
Y1-0.02X1-0.04X2-0.13X3-0.08X4-0.06X5+0.08X7+0.03X8-0.15X9-0.1X100.02X12-0.07X13-0.14X14-0.22X15-0.04X17-0.1X18-0.04X19-0.08X21+0.06X220.14X23-0.08X25-0.01X27-0.04X28+0.06X29-0.09X30>=0
……….
………..
………..
Y36-0.13X1-0.14X2-0.12X3-0.12X4-0.1X5-0.28X6-0.32X7-0.17X8-0.09X9-0.19X100.28X11-0.2X12-0.16X13+0.04X14-0.18X15-0.11X16-0.06X17-0.22X18-0.1X190.21X20-0.12X21-0.35X22-0.12X23-0.19X24-0.14X25-0.03X26-0.12X27-0.34X280.19X29-0.1X30>=0
n
Kısıt 4:
j =1
rj x j ατ ρM 0
α [0,1]
80
0.023X1+0.016X2+0.026X3+0.034X4+0.004X5-0.005X6+ 0.02X7+ 0.018X8+
0.026X9+0.035X10+0.03X11+0.012X12+0.02X13+0.031X14+0.031X15+0.018X16+0
.015X17+0.006X18+0.034X19-0.003X20+ 0.02X21+0.027X22+ 0.055X23+
0.013X24+0.015X25+0.007X26+0.019X27+0.025X28+0.01X29+0.023X30-0.035 α
>=0.02
n
Kısıt 5:
xj
M0
j =1
X1+X2+X3+X4+X5+X6+X7+X8+X9+X10+X11+X12+X13+X14+X15+X16+X17+X
18+X19+X20+X21+X22+X23+X24+X25+X26+X27+X28+X29+X30=1
n
Kısıt 6:
x jFj
Fort
j =1
10.63X1+9.82X3+8.25X10+9.41X11+9.19X12+9.47X19+12.39X22+7.47X28+13.06X
30<=10.29
12.74X21+8.57X26<=11.64
8.43X5+4.77X6+3.64X13+6.09X17+10.38X18+53.46X20+14.20X24<=10.34
15.43X8<=17.34
9.85X14<=17.47
4.51X7+18.47X16+8.32X27<=48.85
16.79X9+3.58X15<=6.21
51.39X2+9.1X25+17.13X29<=14.85
23.56X4<=33.29
4.98X23<=4.51
n
Kısıt 7:
x jA kj
Aj
k =1,2,3
j =1
4083087.861X2-22415288.72X2+384171236.4X2<=115692602.6
69444688.69X3-92484833.32X3+491243764.5X3<=111141293.8
124214.9103X4-265069.7183X4+6861701.461X4<=2428063.447
370859560.3X5-755229525.7X5+944882743.9X5<=146265745.3
81
5909450.93X7-13746486.56X7+256935794.8X7<=71197175.17
11607908.13X8-21915972.84X8+43825917.59X8<=9877847.303
62062024.4X9+15082501.52X9+192458810.1X9<=158666350
826965623.4X10-1979379356X10+2923401088X10<=1395213604
106587469.1X11-247873414.6X11+495019288.9X11<=229855079.2
132948278.9X13-217674338.5X13+507978513.3X13<=304280736.9
26625739.4X14-104136434.4X14+669738422.2X14<=150946501.4
162468352.6X16-15230264.47X16+58539386X16<=202979872
88481643.64X17-24093616.23X17+153676052.9X17<=190193810.7
25097977.33X18-2208808.51X18+216502607X18<=98273249.91
44056597.7X19-67020722.19X19+325540092.3X19<=91410680.28
138713795.8X21-83873886.91X21+297397619.8X21<=277899183.7
-921101.9687X22-54020267.75X22+780767926.6X22<=233697201
239979.9136X23-1283556.074X23+562065037.1X23<=198028990
9104473.771X25-25347300.62X25+135150237.6X25<=23381499.43
20329193.27X27-41468.05115X27+119640883.9X27<=76408390.24
Bu modelin LINDO 6.1 paket programıyla çözülmesi sonucu
bulunmuĢtur. Bulunan
= 0,573
değerine karĢılık gelen minimum risk oranı, üyelik
fonksiyonundan aĢağıdaki Ģekilde bulunabilir.
μ z (x) α 1 [Z 0, 041] / 0,078
0,573 1 [Z 0, 041] / 0,078
1 0,573 [Z 0, 041] / 0,078
0,333*0, 078 Z 0, 041
Z 0, 0743
= 0,573 memnuniyet seviyesinde minimize edilen risk oranı (Z) %7,43 olarak
bulunmuĢtur. Bu memnuniyet seviyesindeki beklenen getiri oranı ise,
Beklenen Getiri Oranı
ρM 0 ατ
0,02+0,573*0,035
0,04
82
= 0,573 memnuniyet seviyesinde, %7,43 risk ile elde edilecek beklenen getiri oranı
%4 „ tür. Çizelge 4.2‟ de, oluĢturulan önerilen modelin çözülmesi sonucu oluĢturulan
portföyde bulunması gereken hisse senetleri ve portföy içindeki miktarları (%)
görülmektedir.
Çizelge 4.2. Önerilen modelin çözülmesi sonucu elde edilen portföydeki hisse senetleri ve oranları
xj
Hisse Senedi
Portföy Ġçindeki Payı (%)
x4
BIMAS
36,2
x9
EREGL
4,3
x10
GARAN
7,8
x14
KOZAA
11,2
x 21
TCELL
5,3
x 23
THYAO
35,2
Elde edilen sonuçlara göre oluĢturulacak portföyde, %36,2‟ lik oranla Bim
BirleĢik Mağazalar A.ġ. hissesi, %4,3 Ereğli Demir ve Çelik Fabrikaları Tic. A.ġ.
hissesi, %7,8 Garanti Bankası A.ġ. hissesi, %11,2 Koza Davetiye Mağaza ĠĢletmeleri ve
Ġhracat A.ġ. hissesi, %5,3 Turkcell ĠletiĢim ĠĢletmeleri A.ġ. hissesi, %35,2 Türk
Havayolları A.O hisseleri yer almalıdır.
4.2. Önerilen Modelin Opsiyonlu Alım Durumunda Değerlendirilmesi
Bu kısımda, önerilen modele VOB‟ da iĢlem gören endeks sözleĢmesinin
opsiyonlu alım durumu da eklenerek sonuçların nasıl değiĢeceği sayısal bir örnekle
açıklanacaktır.
Varsayım 1: Elinde 100.000 TL olan bir yatırımcı parasının tamamını ĠMKB 30
endeksinde yer alan ve modelin çözülmesi sonucu oluĢturulan portföye yatırdığı
taktirde, %7,43‟ lük bir risk oranı ile 4.000 TL getiri elde edebilir.
83
Anapara
= 100.000 TL
Risk
= %7,43
Beklenen Getiri (%4)
= 4.000 TL
Varsayım 2: Aynı yatırımcı varlığının bir kısmını oluĢturulan portföye yatırıp,
kalan kısmı ile Vadeli ĠĢlem ve Opsiyon Borsası‟ nda opsiyonlu alım yöntemini
kullanarak, 2009 yılında 111F_IX0301209 kodlu ĠMKB 30 endeks sözleĢmesini satın
aldığı taktirde,
SözleĢme tarihi
= 02.01.2009
Endeksin cari piyasa fiyatı
= 35,125 TL
Opsiyon kullanma fiyatı
= 39,7 TL
Opsiyon primi
= ? (Hesaplanacak değer)
Vade sonu tarihi
= 31.12.2009
Yatırımcı, 02.01.2009 tarihinde 35,125 TL olan ĠMKB 30 endeks sözleĢmesinin,
31.12.2009 tarihinde 39,7 TL‟ nin üzerine çıkacağını düĢünerek bu fiyattan opsiyonlu
alım yapmıĢtır. Opsiyonlu alım iĢlemi yapılırken belirli bir miktarda opsiyon primi
yatırılması gerekmektedir. Opsiyon primi, Black & Scholes modeli yardımıyla,
VC
d1
d2
C S0 N(d1 ) Ee
rT
N(d 2 )
ln(S0 /E) (r (1/2)σ 2 )T
σ T
d1 σ T
eĢitliklerinden hesaplanmaktadır.
Burada,
VC : Satın alma opsiyonunun fiyatı,
N(d1 ), N(d 2 ) : Normal dağılım tablosunda d1 ve d2 ‟ ye karĢılık gelen değerlerdir.
S0 : Cari hisse senedi (endeks) fiyatı,
E
: Opsiyon kullanma fiyatı,
84
r
: Risksiz faiz oranı,
σ
: Hisse senedinin (endeksin) getiri oranlarının yıllık standart sapması,
T
: Opsiyonun bitimine kadar kalan zaman,
e
: Doğal logaritma fonksiyonunun tabanı,
e
ln
rT
: Ġskonto oranı,
: Doğal logaritma fonksiyonu.
Risksiz faiz oranı, 05.01.2009 tarihinde alınan 18.11.2009 vadeli devlet
tahvilinin getirdiği faiz oranı %15,95‟ dir.
ĠMKB 30 endeksinin 36 aylık getirilerinin standart sapması 0,1122 olarak
bulunmuĢtur. Black & Scholes modelinde bu değer, yıllık standart sapma olarak ifade
edilmektedir. Bu sebeple aylık standart sapma değerini, yıllık standart sapma değeri;
Yıllık standart sapma değeri ( σ ) = Aylık standart sapma değeri * 12
= 0,1122* 12
= 0,3887
Ģeklinde gösterilmektedir.
Black & Scholes modelinin çözümü için gerekli veriler Ģunlardır:
Risksiz faiz oranı
= 0,1595
Opsiyonun bitimine kadar kalan zaman
= 251/365 = 0,6876 yıl
Endeksin cari piyasa fiyatı
= 35,125 TL
Opsiyon kullanma fiyatı
= 39,7 TL
Endeks getiri oranlarının yıllık standart sapması = 0,3887
Opsiyon fiyatının hesaplandığı tarih
= 02.01.2009
Opsiyonun vadesi
= 31.12.2009
Bulunan değerler Black & Scholes modelindeki d1 ve d 2 denklemlerinde yerlerine
koyulursa;
85
d1
ln(S0 /E) (r (1/2)σ 2 )T
σ T
d1
ln(35,125/39,7) (0,1595 (1/2)(0,151098))(251/365)
0,388714 (251/ 365)
d1
0,121
d2
d1 σ T
d2
0, 2
d1 ve d2 değerleri, normal dağılım tablosundan,
N(d1 )
N(0,121) 0,54819
N(d 2 )
N( 0, 2) 0, 4207
elde edilir. d1 ve d 2 ile birlikte diğer verilerinde satın alma opsiyon fiyatı denkleminde
yerine koyulmasıyla,
rT
VC
C S0 N(d1 ) Ee
N(d 2 )
VC
35,125*(0,54819) 39, 7 *e
VC
4, 29 TL
0,1595*0,6876
*(0, 4207)
olarak bulunur.
1 adet ĠMKB 30 endeks sözleĢmesinin değeri, opsiyon kullanma fiyat ile
opsiyon priminin toplamının 100 ile çarpılması ile bulunur.
SözleĢmenin değeri = (Opsiyon kullanma fiyatı + opsiyon primi) * 100
= (39,7 + 4,29) * 100
= 4.399 TL
86
Yatırımcı, elindeki 100.000 TL‟ nin 43.990 TL‟ si ile VOB‟ da 10 adet
opsiyonlu ĠMKB 30 endeks sözleĢmesi alıp, 56.010 TL‟ lik kalan miktarı ise önerilen
model yardımıyla oluĢturulan portföye yatırırsa;
VOB‟ a yatırılan anapara
= 43.990 TL
Opsiyon primi (risk)
= 4.290 TL
Opsiyon tarihi sonundaki beklenen endeks fiyatı = 46,55 TL
Beklenen Getiri
= (46,55-39,7)*100*10 = 6.850 TL
ĠMKB 30 endeksin cari fiyatı ile opsiyon sözleĢmesinin kullanım fiyatı farkının
100 ile çarpılması sonucunda 1 adet sözleĢmeden elde edilen getiri miktarı bulunur.
Opsiyon tarihi sonunda ĠMKB 30 endeksinin yatırımcı tarafından beklenilen değeri
46,55 TL olduğu bilinmektedir. Yatırımcı 10 adet ĠMKB 30 endeks sözleĢmesi satın
aldığı için getiri miktarı 6.850 TL olmaktadır. Opsiyon tarihi sonunda ĠMKB 30 endeks
değerinin
kullanım
fiyatı
altına
düĢmesi
durumunda
yatırımcı
opsiyonu
kullanmayacaktır. Böylece kaybı maksimum 4.290 TL olacaktır.
ĠMKB‟ ye yatırılan anapara
= 56.010 TL
Risk
= %7,43
Beklenen getiri (%4)
= 2.240,4 TL
Yatırımcı kalan miktarı oluĢturulan portföye yatırdığı taktirde %7,43‟ lük bir
risk oranı ile 2.240,4 TL getiri elde edebilir. Çizelge 4.3‟de, varsayım-1 ve varsayım-2
durumları için risk ve getirileri karĢılaĢtırılmıĢtır.
87
Çizelge 4.3. Varsayım-1 ve Varsayım-2 için risk/getiri durumu
Varsayım-1
Varsayım-2
ĠMKB 30
ĠMKB 30
VOB
100.000
56.010
43.990
Risk (%)
7,43
7,43
-
Risk (TL)
-
-
4.290
Beklenen Getiri (%)
4
4
15,571
Beklenen Getiri (TL)
4.000
2.240,4
6.850
Yatırım Yeri
Yatırım Tutarı (TL)
Çizelge 4.3‟ e göre, Varsayım-1 için %7,43‟ lük risk oranı ile elde edilebilecek
getiri miktarı %4‟ tür. Yani, 4.000 TL‟ lik beklenen getiriye karĢılık 7.430 TL‟ lik risk
bulunmaktadır. Varsayım-2 için, ĠMKB 30 ve VOB‟ da ayrı ayrı %7,43 ve %9,75‟lik
risk oranlarına karĢılık %4 ve %15,571‟ lik getiri elde etmek mümkündür. Bu risk
oranlarına karĢılık beklenen getiri miktarları ise 2.240,4 TL ve 6.850 TL‟ dir. Buradaki
yatırım kararı, her zaman olduğu gibi yatırımcıya kalmaktadır. Riski seven bir yatırımcı
yüksek bir risk oranı ile yüksek getiri elde edebilirken, risk almaktan kaçınan bir
yatırımcı daha düĢük bir risk oranı ile daha az getiri elde edebilir.
88
5. SONUÇLAR VE ÖNERĠLER
Portföy kavramının temelinde risklerin minimize edilmesi fikri yatmaktadır. Bu
sebepten dolayı yatırımların tek bir menkul kıymet yerine, birden fazla menkul
kıymetten oluĢan bir portföye yatırılması cazip gelmektedir. Elbette ki bu çeĢitlendirme,
portföy içindeki hisse senetlerinin birbirleri ile ya da içinde bulunduğu sektör ile
kıyaslanarak yapılmalıdır. Böylece elde edilen getiri beklenen getiriye daha fazla
yaklaĢılmıĢ olacaktır.
Markowitz 1952 yılındaki çalıĢmasıyla yatırımcılar için yepyeni ufuklar
açmıĢtır. Zamanla Markowitz‟ in çalıĢmaları üzerinden yeni varsayımlar ve yaklaĢımlar
türetilmiĢtir. Bu yaklaĢımlardan biri olan Konno-Yamazaki doğrusal programlama
modeli, Werners ve diğer araĢtırmacılar tarafından bulanıklaĢtırılmıĢtır.
Bu çalıĢmada, portföy optizasyonuna bulanık doğrusal programlama yaklaĢımını
kullanan Werners‟ ın modeli esas alınmıĢtır. Bu modele, hisse senetlerinin sektördeki
durumları ve geçmiĢteki performansları incelenerek, temel analiz yöntemlerinden biri
olan Fiyat/Kazanç oranı ve teknik analiz yöntemlerinden Toplama-dağıtım endeksi kısıt
olarak eklenerek yeni bir model oluĢturulmuĢtur.
Önerilen modelin LINDO 6.1 paket programı yardımıyla çözülmesi sonucunda
bir portföy elde edilmiĢtir. Bu portföyde, %36,2‟ lik oranla Bim BirleĢik Mağazalar
A.ġ., %4,3 Ereğli Demir ve Çelik Fabrikaları Tic. A.ġ., %7,8 Garanti Bankası A.ġ.,
%11,2 Koza Davetiye Mağaza ĠĢletmeleri ve Ġhracat A.ġ., %5,3 Turkcell ĠletiĢim
ĠĢletmeleri A.ġ., %35,2 Türk Havayolları A.O hisseleri yer almaktadır. OluĢturulan bu
portföyün %7,43‟ lük bir risk ile %4 getiri elde etmesi beklenmektedir.
Daha sonra Vadeli ĠĢlem ve Opsiyon Borsası‟nda iĢlem gören ĠMKB 30 endeks
sözleĢmesinin opsiyonlu alım durumunda kullanılmasıyla kar ve zararın ne Ģekilde
değiĢeceği sayısal bir örnekle açıklanmıĢtır.
Elinde 100.000 TL anaparası olan bir yatırımcı olduğu varsayılmıĢtır. Bu
yatırımcı varsayım-1 de anaparasının tamamını önerilen modelin çözülmesi sonucu elde
edilen portföye yatırmıĢtır. Bunun sonucunda %7,43‟ lük risk ile 4.000 TL getiri elde
etmesi beklenmektedir. Varsayım-2 de ise elindeki yatırım tutarının 43.990 TL‟ si ile
ĠMKB 30 endeks sözleĢmesini opsiyonlu alım durumunda alıcı pozisyonunda kullanıp,
geriye kalan 56.010 TL‟ lik miktarı modelin çözülmesi sonucu oluĢturulan portföye
yatırırsa 9.090.4 TL getiri elde etmektedir. Buradaki 43.990 TL için 4.290 TL, 56.010
TL için %7,43‟ lük bir risk bulunmaktadır.
89
Ġncelenen dönemde opsiyonlu alım durumunda, yatırımcının biraz daha fazla
oranda riski göze alması durumunda oldukça fazla bir getiri elde etmesi mümkündür.
Bunun kararını verecek olan her zamanki gibi yatırımcıdır.
Bu çalıĢmada ĠMKB 30 endeksine dahil olan hisse senetlerine yönelik bir
portföy oluĢturulmuĢtur. Bundan sonraki çalıĢmalarda farklı yatırım araçları (döviz,
repo, altın, hazine bonosu, devlet tahvili vb.) da kullanılarak geniĢ seçim olasılıkları
olan bir portföy oluĢturulabilir. Ayrıca VOB‟ da kullanılan sözleĢme türleri (döviz
vadeli iĢlem sözleĢmeleri, endeks vadeli iĢlem sözleĢmeleri, faiz vadeli iĢlem
sözleĢmeleri, emtia vadeli iĢlem sözleĢmeleri) de bu iĢleme dahil edilerek kompleks bir
portföy oluĢturulabilir.
Hisse senetleri için bir portföy oluĢturulmak isteniyorsa, teknik analiz ve temel
analiz yöntemleri incelenerek uygun görülen yöntemler, hisse senedi seçiminde
değerlendirme kriteri olarak kullanılabilir.
90
KAYNAKLAR
AkbaĢ, C., 1999, Hisse senedi portföy yönetimi ve portföy takip programı, Yüksek
Lisans Tezi, Atatürk Üniversitesi Sosyal Bilimler Enstitüsü, Erzurum.
Akgüç, Ö., 1998, Finansal yönetim, Muhasebe Enstitüsü Yayınları, Yayın No:65, 7.
Baskı, Ġstanbul, 82-86.
Alpan, F., 1999, Örneklerle futures anlaĢmalar ve opsiyonlar, Literatür Yayınları:26,
Ġstanbul,143-148.
Amiri, M.N., Nasseri, S.H., 2006, Duality in fuzzy number linear programming by use
of a certain linear ranking function, Applied Mathematics and Computation, Vol.
180, 206-216.
Ammar, E., Khalifa, H.A., 2003, Fuzzy portfolio optimization a quadratic programming
approach, Chaos, Solitons and Fractals, 18, 1045-1054.
Anonim, 2002, Sermaye piyasası faaliyetleri ileri düzey lisans eğitimi-finansal yönetim
[online],
Türkiye
Sermaye
Piyasası
Aracı
KuruluĢları
Birliği,
http://www.tspakb.org.tr/egitim/notlari/finansal_yoneyim_ileri.pdf,
[Ziyaret
Tarihi: 10 Haziran 2009].
Anonim, 2007, Muhasebe ve finansman türev piyasa araçları, T.C. Milli Eğitim
Bakanlığı Mesleki Eğitim ve Öğretim Sisteminin Güçlendirilmesi Projesi, Ankara.
Anonim, 2007, Vadeli iĢlem ve opsiyon sözleĢmeleri [online], Sermaye Piyasası Kurulu
Yatırımcı
Bilgilendirme
Kitapçıkları-8,
http://www.spk.gov.tr/displayfile.aspx?action=displayfile&pageid=77&fn=77.pdf
[Ziyaret Tarihi: 14 Haziran 2010].
Anonim, 2008, Sermaye piyasası kanununa tabi ortaklık ve kuruluĢların yükümlülükleri
[online], ĠMKB Eğitim Seti, http://www.imkb.gov.tr/training/TrainingSets.aspx,
[Ziyaret Tarihi:17 Mayıs 2010].
Anonim, 2010, Yatırımcı rehberi [online], Vadeli ĠĢlem ve Opsiyon Borsası,
http://www.vob.org.tr/VOBPortalTur/docs/yatirimci_rehberi.pdf, [Ziyaret Tarihi:
11 Temmuz 2010].
Apaydın, F., 2009, Teknik analizde optimizasyon uygulaması ve bu uygulamanın
ĠMKB üzerinde test edilmesi, Yüksek Lisans Tezi, Marmara Üniversitesi Sosyal
Bilimler Enstitüsü, Ġstanbul.
AslantaĢ, C., 2008, Portföy yönetiminde fuzzy yaklaĢımı, Yüksek Lisans Tezi,
Marmara Üniversitesi Sosyal Bilimler Enstitüsü, Ġstanbul.
Aydoğan, K., Güney, A., 1996, Hisse senedi fiyatlarının tahmininde F/K oranı ve
temettü verimi, İMKB Dergisi, Cilt:1 No:1.
91
Badhani, K.N., Suyal, J., 2005, Stock price-volume causality at index level [online],
http://papers.ssrn.com/sol3/papers.cfm?abstract_id=874914, [Ziyaret Tarihi: 14
Mayıs 2010].
Balaban, E., 1995, Opsiyonlar, Türkiye Cumhuriyet Merkez Bankası Araştırma Genel
Müdürlüğü, TartıĢma Tebliği No: 9501, Ankara.
Basu, S., 1977, Investment performance of common stocks in relation to their priceearnings ratios: A test of the efficient market hypothesis, The Journal of Finance,
Vol. 32, 663–682.
BaĢçı, E., Özyıldırım, S., Aydoğan, K., 1996, A note on price-volume dynamics in an
emerging stock market, Journal of Banking and Finance, Vol. 20, No: 2, 389-400.
BaĢtürk, F., H., 2004, F/K oranı ve firma büyüklüğü anomalilerinin bir arada ele
alınarak portföy oluĢturulması ve bir uygulama örneği, Anadolu Üniversitesi
Yayınları, No: 1564, EskiĢehir.
Bekçi, Ġ., 2001, Optimal portföy oluĢturulmasında bulanık doğrusal programlama
modeli ve ĠMKB‟ de bir uygulama, Doktora Tezi, Süleyman Demirel Üniversitesi
Sosyal Bilimler Enstitüsü, Isparta.
Berk, N., 2000, Finansal yönetim, Türkmen Kitabevi, 5. Basım, Yayın No: 62, Ġstanbul.
BeĢer, M., 2005, Kuadratik programlama tabanlı modelleme yardımı ile portföy
optimizasyonu ve ĠMKB-30 portföy oluĢturma uygulaması, Yüksek Lisans Tezi,
İstanbul Üniversitesi Sosyal Bilimler Enstitüsü, Ġstanbul.
Bozdağ, N., Altan, ġ., Duman, S., 2005, Minimaks portföy modeli ile markowitz
ortalama-varyans portföy modelinin karĢılaĢtırılması, VII. Ulusal Ekonometri ve
İstatistik Sempozyumu, Ġstanbul.
Brailsford, T.J., 1994, The empirical relationship between trading volume, returns and
volatility, Department of Accounting and Finance, University of Melbourne,
Avustralya.
Carlsson, C., Korhonen, P., 1986, A parametric approach to fuzzy linear programming,
Fuzzy Sets and Systems, Vol. 20, 17-30.
Ceylan, A., Korkmaz, T., 1998, Borsada uygulamalı portföy yönetimi, Ekin Kitabevi
Yayınları, 3. Baskı, Bursa.
Chanas, S., 1983, The use of parametric programming in fuzzy linear programming,
Fuzzy Sets and Systems, Vol. 11, 243-251.
Chang, C.T., 2005, A modified goal programming approach for the mean-absolute
deviation portfolio optimization model, Mathematics and Computation, 171, 567–
572.
92
Chiang, J., 2001, Fuzzy linear programming based on statistical confidence interval and
interval-valued fuzzy set, European Journal of Operation Research, 129, 65-86.
Delgado, M., Verdegay, J.L., Vila, M.A., 1989, A general model for fuzzy linear
programming, Fuzzy Sets and Systems, Vol. 29, 21-29.
DemirtaĢ, Ö., Güngör, Z., 2004, Portföy yönetimi ve portföy seçimine yönelik
uygulama, Havacılık ve Uzay Teknolojileri Dergisi, Cilt 1, Sayı 4, 103-109.
Deng, F.L., 2011, Linear programming approach to solve interval-valued matrix games,
The International Journal of Management Science, Vol. 39, Issue 6, 655-666.
Erdinç, Y., 1998, Borsada analiz, Siyasal Kitabevi, Ankara, 185-214.
Eroğlu, G., 2006, Portföy analizinde bulanık programlama, Yüksek Lisans Tezi, Ankara
Üniversitesi Fen Bilimleri Enstitüsü, Ankara.
Fang, Y., Lai, K.K., Wang, S.Y., 2005, Portfolio rebalancing model with transaction
costs based on fuzzy decision theory, European Journal of Operation Research,
879-893.
Fang, L.L., Ji, X.X., Xin, C.W., 2010, A new algorithm for solving fuzzy linear
programming, 2010 Second International Conference on Computer Modeling and
Simulation, Çin, 125-127.
Gallea, A.M., Patalon, W., 1998, KarĢıt yatırım: zor dönemlerde yatırım stratejileri,
Çeviren:Ali PerĢembe, Scala Yayıncılık, 1. Baskı, Ġstanbul, 83-97.
Gasimov, R.N., Yenilmez, K., 2002, Solving fuzzy linear programming problems with
linear membership functions, Turk J Math, 26, 375-396, Tübitak.
Genel, H., 2004, Genetik algoritmalarla portföy optimizasyonu, Yüksek Lisans Tezi,
Ankara Üniversitesi Sosyal Bilimler Enstitüsü, Ankara.
Guu, S., Wu, Y., 1999, Two-phase approach for solving the fuzzy linear programming
problems, Fuzzy Sets and Systems, Vol. 107, Issue 2, 191-195.
Günak, N., 2007, Ġleri teknik analiz uygulamaları, Literatür Yayınları, Ġstanbul. 145148.
Halıcı, B., 2008, Portföy seçimi problemi üzerine karĢılaĢtırmalı alternatif yaklaĢımlar,
Yüksek Lisans Tezi, Gazi Üniversitesi Sosyal Bilimler Enstitüsü, Ankara.
Harney, M., Tower, E., 2003, Rational pessimism: predicting equity returns using
Tobin‟s q and price/earnings ratios, The Journal of Investing (forthcoming),
January 2, 3-11.
Hasuike, T., Katagiri, H., Ishii, H., 2009, Portfolio selection problems with random
fuzzy variable returns, Fuzzy Sets and Systems, 160, 2579-2596.
93
Horasan, M., 2009, Fiyat/kazanç oranının hisse senedi getirilerine etkisi: ĠMKB 30
endeksi üzerine bir uygulama, Atatürk Üniversitesi İktisadi ve İdari Bilimler
Dergisi, Cilt: 23, Sayı: 1, Erzurum.
Huang, X., 2007, Mean-semivariance models for portfolio optimization, Journal of
Computational And Applied Mathematics, 217, 1-8.
Huang, X., 2007, Risk curve and fuzzy portfolio selection, Journal of Computational
And Applied Mathematics, 55, 1102-1112.
Inuiguchi, M., Sakawa, M., 1998, Robust optimization under softness in a fuzzy linear
programming problem, International Journal of Approximate Reasoning, 21-34.
Inuiguchi, M., Ramik, J., 1998, Possibilistic linear programming: A brief review of
fuzzy mathematical programming and a comparison with stochastic in portfolio
selection problem, Fuzzy Sets and Systems, 111, 3-28.
Ġpekten, O.B., 1992, Menkul kıymetler yatırım ortaklıkları ve yatırım fonlarının
sermaye piyasasının geliĢimine katkıları, Doktora Tezi, Atatürk Üniversitesi
Sosyal Bilimler Enstitüsü, Erzurum.
Jacobs B. I., Levy K. N., Starer D., 1999, Long – short portfolio management: An
integrated approach, The Journal of Portfolio Management, Vol: 25, No: 2, 17-23.
Jamison, K.D., Lodwick, W.A., 2001, Fuzzy linear programming using a penalty
method, Fuzzy Sets and Systems, 119(1), 97-110.
Javid, A. and Mubarik, F., 2009, Relationship between stock return, trading volume and
volatility: Evidence from Pakistani stock market, Asia Pacific Journal of Finance
and Banking Research. 3(3), 1-17.
Kamath, R.R., 2008, The price-volume relationship in the chilean stock market.
International Business & Economics Research Journal, Vol. 7, No: 10.
Kane, A., Marcus A.J., Noh, J., 1996, The P/E multiple and market volatility, Financial
Analysts Journal, Vol:52, No:4,16–25.
Karan, M.B., 2001, Yatırım analizi ve portföy yönetimi, Gazi Kitabevi, Hüfam
Yayınları, No:1, Ankara, 72-85.
Karpoff, J.M., 1987, The relation between price changes and trading volume: A survey,
Journal of Financial and Quantitative Analysis, Vol 22, No 1, 109-126.
Kıran, B., 2010, Ġstanbul menkul kıymetler borsasında iĢlem hacmi ve getiri volatilitesi,
Doğuş Üniversitesi Dergisi, 11 (1), Ġstanbul, 98-108.
Kocadağlı, O., 2006, Bulanık matematiksel programlama ve portföy analizi uygulaması,
Yüksek Lisans Tezi, Mimar Sinan Üniversitesi Güzel Sanatlar Fakültesi Fen
Bilimleri Enstitüsü, Ġstanbul.
94
Konno, H., Yamazaki, H., 1991, Mean-absolute deviation portfolio optimization model
and its applications to Tokyo stock market, Management Science, Vol. 37, No. 5,
A.B.D.
Korkmaz, T., 1999, Hisse senedi opsiyonları ve opsiyon fiyatlama modelleri, Ekin
Kitabevi Yayınları, Bursa, 110-132.
Koulakiotis, A., Papasyriopoulos, N., Molyneux, P., 2006, More evidence on the
relationship between stock price returns and volatility: A note, International
Research Journal of Finance and Economics, ISSN 1450-2887, Issue 1.
Lee, B-S., Rui, O.M., 2002, The dynamic relationship between stock returns and trading
volume: Domestic and cross-country evidence, Journal of Banking and Finance,
26, 51-78.
Lotfi, F.H., Allahviranloo, T., Jondabeh, M.A., Alizadeh, L., 2009, Solving a full fuzzy
linear programming using lexicography method and fuzzy approximate solution,
Applied Mathematical Modelling, 3151-3156
Markowitz, H., 1952, Portfolio selection, Journal of Finance, Vol. VII, No.1, A.B.D.
Nakamura, K., 1984, Some extensions of fuzzy linear programming, Fuzzy Sets and
Systems, Vol. 14, 211-229.
Negoita, C.V., 1981, Fuzzy systems [online]. Cybernetics and Systems Series, Abacus
Pres,http://www.google.com/books?id=1VGIIk9qoEC&lpg=PA1&ots=nGf7ypxPXk&dq=robust%20yazar%3ANegoita&lr=&
hl=tr&pg=PP1#v=onepage&q=&f=false, [Ziyaret Tarihi: 29 Nisan 2010].
Östermark, R., 1996, A fuzzy control model (FCM) for dynamic portfolio management,
Fuzzy Sets and Systems, 78, 23-254.
Öztürk, A., 1997, Yöneylem araĢtırması, Ekin Kitabevi Yayınları, 5. Baskı, Bursa.
Öztürk, B., 2007, Fiyat/Kazanç oranını etkileyen değiĢkenler üzerine ĠMKB‟ de ampirik
bir uygulama, Sosyal Bilimler Enstitüsü Dergisi, Say:23, 2007/2, Niğde, 275-284.
Paksoy, T., 2002, Bulanık küme teorisi ve doğrusal programlamada kullanımı:
KarĢılaĢtırmalı bir analiz, Selçuk Üniversitesi Mühendislik Mimarlık Fakültesi
Dergisi, Cilt 17, No 1, Konya, 1-16.
Parra, A.M., Terol, B.A., Uria, R.V.M., 2001, A fuzzy goal programming approach to
portfolio selection, European Journal of Operation Research, 133, 287-297.
Pelitli, D., 2007, Portföy analizinde bulanık mantık yaklaĢımı ve uygulama örneği,
Yüksek Lisan Tezi, Pamukkale Üniversitesi Sosyal Bilimler Enstitüsü, Denizli.
PerĢembe, A., 2006, ĠĢlem hacmi [online], Dünya Gazetesi,
http://www.persembe.com/MAKALE/Makale9.htm, [Ziyaret Tarihi: 01 Haziran
2010].
95
Ramaswamy, S., 1998, Portfolio selection using fuzzy decision theory, Working Paper
of Bank for International Settlements, No.59, 17-23.
Rashid, A., 2007, Stock prices and trading volume: An assessment for linear and
nonlinear granger causality, Journal of Asian Economics, Vol. 18, Issue: 4, 595612.
Rommelfanger, H., Hanuscheck, R., Wolf, J., 1989, Linear programming with fuzzy
objectives, Fuzzy Sets and Systems, Vol. 29, 31-48.
Sadeghi, M., Hosseini, H.M., 2004, Energy supply planning in iran by using fuzzy
linear programming approach, Energy Policy, 34, 993-1003.
Sadjadi, S.J., Seyedhosseini, S.M., Hassanlou, Kh., 2011, Fuzzy multi period portfolio
selection with different rates for borrowing and lending, Applied Soft Computing
Serper, Ö., 1986, Uygulamalı istatistik 2, Filiz Kitabevi, 2. Baskı, Ġstanbul, 201-231.
Sevil, G., 2001, Finansal risk yönetimi çerçevesinde piyasa volatilitesinin tahmini ve
portföy var hesaplamaları [online], http://home.anadolu.edu.tr/~gsevil/VaR.pdf,
[Ziyaret Tarihi: 18 Mayıs 2010].
Sezgin, F.H., 2008, Portföy seçiminde veri zarflama analizi ile diskriminant analizi
yöntemlerinin
karĢılaĢtırmalı
etkinliği
[online].
http://bandirma.balikesir.edu.tr/bildiriler/31_Funda_Sezgin.doc,
[Ziyaret
Tarihi:13 Nisan 2010].
Shaocheng, T., 1994, Interval number and fuzzy number linear programming, Fuzzy
Sets and Systems, Vol. 66, 301-306.
Shen, P., 2000, The P/E ratio and stock market performance, Economic Review-Federal
Reserve Bank of Kansas City, Vol:85, No:4, A.B.D.
ġen, Z., 2004, Mühendislikte bulanık (fuzzy) mantık ile modelleme prensipleri, Ġ.T.Ü.
Uçak ve Uzay Bilimleri Fakültesi, Su Vakfı Yayınları, Ġstanbul, 16-19.
Tanaka, H., Asai, K., 1984, Fuzzy linear programming problems with fuzzy numbers,
Fuzzy Sets and Systems, Vol. 15, 3-10.
Taner, B., Akaya, C., 2003, ĠĢletme değerini belirleme yöntemleri ve farklı
sektörlerdeki iĢletmeler üzerine bir uygulama, Ege Akademik Bakış Dergisi, Cilt:3
Sayı:1-2, Ġzmir.
Théoret, R., Racicot, F.E., 2010, Forecasting stochastic volatility using the Kalman
filter: An application to Canadian interest rates and price-earnings ratio, The IEB
International Journal of Finance, 28-47.
Trevino, R., Robertson, F., 2002, P/E ratios and stock market returns, Journal of
Financial Planning, 15(2), 76–84.
96
Tural, Ö., 2008, Riskten korunmada opsiyon sözleĢmeleri fiyatlandırma modeli
uygulamaları. Yüksek Lisans Tezi, Marmara Üniversitesi Bankacılık ve
Sigortacılık Enstitüsü, Ġstanbul.
Turan, G., 2001, Ġki amaçlı portföy seçim problemi, Yüksek Lisans Tezi, İstanbul
Üniversitesi Sosyal Bilimler Enstitüsü, Ġstanbul.
Turanlı, M., Özden, Ü.H., Demirhan, D., 2002, Seçim tartıĢmalarının hisse senedi
piyasasına
etkisi
[online],
Ġstanbul
Ticaret
Üniversitesi
Dergisi,
http://www.iticu.edu.tr/kutuphane/dergi/d2/M00019.pdf , [Ziyaret Tarihi: 14
Nisan 2010].
Türe, H., 2006, Bulanık doğrusal programlama ve bir uygulama, Yüksek Lisans Tezi,
Gazi Üniversitesi Sosyal Bilimler Enstitüsü, Ankara.
Umutlu, G., 2008, ĠĢlem hacmi ve fiyat değiĢimleri arasındaki nedensellik ve dinamik
iliĢkiler: ĠMKB‟ de bir ampirik inceleme, Gazi Üniversitesi İktisadi ve İdari
Bilimler Fakültesi Dergisi, 10/1, 231-246.
Verdegay, J.L.,1984, A dual approach to solve the fuzzy linear programming model,
Fuzzy Sets and Systems, Vol. 14, Issue 2, 131-141.
Werners, B., 1987, An interactive fuzzy programming system, Fuzzy Sets and Systems,
Vol. 23, 131-147.
Wu, X., Liu, Y., 2010, A class of fuzzy portfolio optimization problems: E-S models,
Lecture Notes in Computer Science, Vol. 6146/2010, 43-50.
Yörük, N., 2000, Finansal varlık fiyatlama modelleri ve arbitraj fiyatlama modelinin
ĠMKB‟de test edilmesi, Cilt No: 18, İstanbul Menkul Kıymetler Borsası, Ġstanbul.
Zimmermann, H.J., 1974, Optimization in fuzzy environment, XXI International TIMS
and 46th ORSA Conference, San Juan, Puerto Rico.
Zimmermann, H.J., 1991, Fuzzy set theory and its applications [online], Kluwer
Academic Publishers, Massachusetts, USA. http://books.google.com.tr/
books?id=Uqtwf6bcUxMC&printsec=frontcover&dq=fuzzy+set+theory+and+its+
application+zimmermann&source=bl&ots=Wv_62GUSgz&sig=yI9MhqArPKGR
mwsMkcg41N-zeto&hl=tr&ei=WhMQTLvrMpKH4Qaz6WPDA&sa=X&oi=book_result&ct=result&resnum=3&ved=0CC0Q6AEwAg#v
=onepage&q=fuzzy%20set%20theory%20and%20its%20application%20zimmer
mann&f=false, [Ziyaret Tarihi: 29 Nisan 2010].
97
EKLER
EK-1 ĠMKB 30 Endeksine Dahil Olan Hisseler ve Sektörleri
Hisse Senedi Adı
Bulunduğu Sektör
AKBNK
ARCLK
ASYAB
BIMAS
DOHOL
DYHOL
ECILC
ENKAI
EREGL
GARAN
HALKB
ISCTR
KCHOL
KOZAA
KRDMD
PETKM
SAHOL
SISE
SKBNK
TAVHL
TCELL
TEBNK
THYAO
TKFEN
TOASO
TTKOM
TUPRS
VAKBN
VESTL
YKBNK
Bankalar ve Özel Finans Kurumları
Metal EĢya, Makine ve Gereç Yapım
Bankalar ve Özel Finans Kurumları
Perakende Ticaret
Holdingler ve Yatırım ġirketleri
Holdingler ve Yatırım ġirketleri
Kimya, Petrol, Kauçuk ve Plastik Ürünler
ĠnĢaat ve Bayındırlık
Metal Ana Sanayi
Bankalar ve Özel Finans Kurumları
Bankalar ve Özel Finans Kurumları
Bankalar ve Özel Finans Kurumları
Holdingler ve Yatırım ġirketleri
Kağıt ve Kağıt Ürünleri, Basım ve Yayın
Metal Ana Sanayi
Kimya, Petrol, Kauçuk ve Plastik Ürünler
Holdingler ve Yatırım ġirketleri
Holdingler ve Yatırım ġirketleri
Bankalar ve Özel Finans Kurumları
Holdingler ve Yatırım ġirketleri
HaberleĢme
Bankalar ve Özel Finans Kurumları
UlaĢtırma
Holdingler ve Yatırım ġirketleri
Metal EĢya, Makine ve Gereç Yapım
HaberleĢme
Kimya, Petrol, Kauçuk ve Plastik Ürünler
Bankalar ve Özel Finans Kurumları
Metal EĢya, Makine ve Gereç Yapım
Bankalar ve Özel Finans Kurumları
98
EK-2 ĠMKB 30 Endeksine Dahil Hisse Senetlerinin Aylık Artım Oranları ( %)
Dönem Sayısı Dönemler AKBNK ARCLK ASYAB BIMAS DOHOL DYHOL ECILC
1
07/01
4,65
2
07/02
3,33
3
07/03
2,74
4
07/04
7,53
5
07/05
6
5,99
16,07
11,33
6,28
-0,60
-6,42
7,91
0,00
-3,59
-3,38
-4,65
12,75
-1,57
22,31
1,86
1,31
8,05
12,17
8,51
0,63
5,49
12,07
0,00
-10,85
-7,50
15,94
-5,00
-6,51
10,77
9,80
5,22
07/06
-1,35
-0,88
5,92
10,13
-8,33
-5,36
0,00
7
07/07
21,23
-3,54
10,56
0,57
6,82
7,55
-9,09
8
07/08
-6,21
-16,06
-4,49
9,14
-11,70
-16,84
-10,18
9
07/09
10,84
7,10
16,47
4,71
6,02
8,65
5,26
10
07/10
15,22
-9,18
0,00
-4,00
-3,03
13,59
-0,96
11
07/11
-18,87
-7,87
-1,01
1,56
-10,55
-12,82
2,91
12
07/12
1,16
-0,61
12,24
7,69
-3,06
-5,13
-1,89
13
08/01
-22,41
-17,79
-10,91
-8,10
-28,83
-26,05
-23,46
14
08/02
-2,96
4,48
17,35
10,88
-1,90
-11,36
14,57
15
08/03
-11,39
-24,29
-27,39
-1,87
-13,55
-26,92
-20,61
16
08/04
18,75
7,55
5,99
10,48
15,67
19,30
7,18
17
08/05
-18,80
-6,80
-6,21
16,05
-7,74
-21,69
2,77
18
08/06
-21,48
-16,08
-28,92
5,45
4,20
-32,86
-0,52
19
08/07
53,30
4,67
28,70
-6,42
16,11
48,25
6,25
20
08/08
-5,38
3,12
-12,16
5,14
0,00
-6,13
-0,74
21
08/09
6,50
-22,08
-22,31
-13,59
-13,29
-25,13
-14,81
22
08/10
-20,31
-39,17
-33,17
-22,01
-18,67
-40,27
5,22
23
08/11
-17,62
-26,48
-7,41
2,42
-6,56
-23,60
-28,93
24
08/12
11,16
27,95
-7,20
1,57
-9,65
-2,94
3,49
25
09/01
0,00
-14,56
-7,76
10,08
-1,68
-3,03
-6,74
26
09/02
-17,99
-1,14
-6,54
-5,63
-17,74
-29,69
-2,41
27
09/03
27,09
5,17
11,00
5,22
7,84
20,00
24,69
28
09/04
27,05
46,45
37,84
24,82
16,36
22,22
19,80
29
09/05
4,03
11,51
18,95
12,34
40,63
63,64
11,24
30
09/06
6,98
6,39
17,58
10,77
24,44
36,11
12,80
31
09/07
20,29
34,76
31,78
7,41
0,00
-1,36
8,51
32
09/08
3,61
36,94
-1,42
-3,45
25,89
26,20
-1,31
33
09/09
0,00
0,00
11,51
8,04
-20,57
-34,15
5,30
34
09/10
-4,65
15,12
1,29
-9,09
-3,13
-1,85
-1,89
35
09/11
0,00
2,02
-3,82
9,79
-7,00
2,83
19,87
36
09/12
15,24
15,84
14,57
15,83
10,75
27,52
33,69
99
Dönem Sayısı Dönemler ENKAI EREGL GARAN HALKB ISCTR KCHOL KOZAA
1
07/01
-1,32
17,78
13,25
3,08
9,09
17,36
2
07/02
12,75
9,43
1,89
0,00
2,50
-17,61
3
07/03
12,50
19,83
15,74
0,00
2,44
0,85
4
07/04
7,94
13,67
7,88
-0,40
7,14
-15,25
5
07/05
10,61
-7,23
8,21
7,50
-6,11
7,41
48,00
6
07/06
0,00
-4,76
1,38
-1,74
0,00
-4,62
20,27
7
07/07
8,00
18,75
22,45
6,51
15,45
14,29
12,36
8
07/08
-11,73
7,37
-7,22
-2,78
-10,56
-0,83
-3,00
9
07/09
6,99
10,78
10,78
12,00
14,96
6,72
19,07
10
07/10
18,95
0,00
15,68
0,51
8,90
0,00
-7,36
11
07/11
4,95
-13,72
-2,34
1,52
-3,77
-5,51
-3,83
12
07/12
7,33
5,64
0,48
22,00
-3,92
5,83
7,14
13
08/01
-19,51
-29,13
-29,52
-29,51
-21,09
-28,19
-22,86
14
08/02
12,73
19,18
-1,35
-9,30
-2,59
1,75
-10,49
15
08/03
-11,83
7,47
-17,81
-5,13
-12,57
-19,83
-18,62
16
08/04
7,32
20,86
14,17
-0,68
23,11
18,28
5,93
17
08/05
10,89
-3,39
-18,25
7,85
-14,58
-10,09
-15,20
18
08/06
-3,42
28,21
-17,14
-21,09
-20,63
-2,91
-14,34
19
08/07
-3,55
-3,50
39,01
37,07
35,00
39,52
14,10
20
08/08
-22,06
-17,10
-9,18
-16,98
5,56
-11,16
-11,20
21
08/09
-17,45
-18,75
-14,04
-12,88
-6,14
-5,31
-48,91
22
08/10
-34,29
-27,08
-17,65
-26,96
-20,00
-27,55
-36,55
23
08/11
-24,52
-21,52
-9,52
-2,38
-6,07
-11,27
-1,09
24
08/12
20,97
10,75
14,04
12,20
1,99
3,97
-3,30
25
09/01
2,86
-13,11
-13,46
-6,96
-10,24
-11,83
3,41
26
09/02
14,81
-3,91
-8,00
-16,36
-10,87
-8,23
52,75
27
09/03
-4,84
-9,30
14,01
1,68
14,02
10,38
15,11
28
09/04
16,10
24,36
42,37
53,85
24,89
24,79
11,25
29
09/05
9,88
9,79
14,29
8,45
14,72
20,55
53,93
30
09/06
-2,95
4,23
8,85
3,39
-4,30
-9,32
5,11
31
09/07
3,73
9,01
24,40
28,69
12,33
30,08
2,78
32
09/08
21,00
22,93
6,73
3,18
16,67
15,03
4,05
33
09/09
4,13
7,56
1,90
8,64
-2,52
-2,01
7,79
34
09/10
-3,17
-10,34
-1,79
2,84
-0,86
-1,54
18,07
35
09/11
-4,92
-2,43
-5,45
0,00
-9,57
-2,60
23,98
36
09/12
18,97
11,94
22,12
31,49
21,15
18,18
-0,82
100
Dönem Sayısı Dönemler KRDMD PETKM SAHOL SISE SKBNK TAVHL TCELL
1
07/01
25,00
1,96
5,41
11,00
7,14
2
3
07/02
9,23
21,15
07/03
18,31
12,70
4
07/04
0,00
5
07/05
6
-2,56
2,70
27,45
3,00
-8,92
0,00
-7,02
-5,38
11,65
-0,70
7,75
6,14
-0,94
16,26
0,87
10,67
11,90
17,65
3,06
4,34
32,87
6,90
16,45
07/06
-3,19
-0,56
6,50
0,93
-1,05
-7,26
0,00
7
07/07
27,47
16,20
11,45
8,33
23,40
9,57
3,39
8
07/08
0,00
-5,29
-1,37
-6,84
20,62
-9,52
3,28
9
07/09
18,97
0,51
7,64
10,09
-3,95
-2,63
7,94
10
07/10
-3,62
-2,53
2,58
-4,35
1,65
-3,60
9,80
11
07/11
0,75
-3,11
-16,98 -10,16
-8,91
3,74
14,29
12
07/12
2,99
-8,02
-2,27
15,56
-3,60
0,00
13
08/01
-28,99
-24,42
-24,03 -29,66 -30,77
-24,30
-20,31
14
08/02
20,41
12,31
13,27
10,56
-5,56
18,63
15
08/03
-12,71
-10,96
-25,05 -13,16 -36,18
-4,58
-8,26
16
08/04
21,36
7,69
14,42
20,00
22,60
-8,11
17
08/05
-4,80
3,57
-0,74
-14,14 -27,28
18,44
-2,99
18
08/06
-3,36
-31,03
-9,91
-23,53
4,85
-23,11
-27,08
19
08/07
5,22
7,00
38,76
23,85
5,04
-4,91
27,14
20
08/08
-7,44
1,87
-13,79
0,00
-9,20
-5,81
-10,67
21
08/09
-28,57
-19,27
-3,60
-2,48
-16,30
-12,33
4,40
22
08/10
-33,75
-5,00
-23,24 -21,02 -35,26
-42,19
-8,43
23
08/11
-13,21
15,79
-16,22 -12,90 -14,63
-16,76
16,45
24
08/12
8,70
-4,55
12,90
0,93
3,81
8,44
-1,13
25
09/01
0,00
-17,75
-9,71
-11,01
-8,26
12,57
1,14
26
09/02
0,00
5,26
-22,15
-2,06
-12,00
-2,82
-4,52
27
09/03
2,00
2,00
16,26
5,26
6,82
5,07
-3,55
28
09/04
37,25
13,24
43,36
25,00
63,83
16,55
0,61
29
09/05
15,71
21,21
15,70
4,80
13,64
11,24
5,48
30
09/06
4,54
16,07
-6,62
5,15
0,71
8,51
4,91
31
09/07
1,89
6,92
32,85
6,35
16,15
0,49
9,36
32
09/08
14,81
2,88
5,45
18,66
30,48
1,95
4,28
33
09/09
1,61
4,90
-0,86
-0,63
2,46
-2,39
8,72
34
09/10
-4,76
-2,67
-3,48
0,63
0,80
1,47
-5,66
35
09/11
-11,67
-10,96
-3,60
-4,40
-9,52
-4,83
-7,00
36
09/12
20,75
12,31
7,48
23,03
13,16
20,30
13,98
2,61
14,46
25,20
9,79
101
Dönem Sayısı Dönemler TEBNK THYAO TKFEN TOASO TTKOM TUPRS VAKBN
1
07/01
-2,86
19,67
9,18
3,31
6,99
2
07/02
3
07/03
18,24
2,74
11,94
-6,67
-1,87
9,00
-4,95
0,95
13,76
0,58
4
07/04
6,67
20,00
14,15
-9,68
10,92
5
07/05
0,83
0,00
5,87
19,60
-0,11
6
07/06
8,03
14,88
0,79
0,80
-6,11
7
07/07
-2,00
0,52
-1,57
1,59
23,67
8
07/08
-2,04
-6,70
-4,80
-7,03
-11,00
9
07/09
10,96
3,87
1,68
7,56
10,75
10
07/10
-1,29
-11,70
1,65
3,13
7,28
11
07/11
-5,23
-4,82
-6,50
-6,82
-13,12
12
07/12
1,38
8,86
7,50
6,96
11,38
7,81
13
08/01
-24,49
-18,02
-0,78
-13,82
-13,87
-30,43
14
08/02
-11,26
3,55
0,78
7,55
5,93
0,00
15
08/03
-29,95
-14,38
2,33
-24,56
-5,60
-15,63
16
08/04
19,57
14,40
19,70
13,02
16,95
7,00
17
08/05
-21,82
-7,69
16,52
0,72
0,00
-1,28
-17,37
18
08/06
-16,83
-24,24
2,73
-24,89
-10,43
-7,38
-24,29
19
08/07
35,24
19,00
-14,36
17,98
3,88
12,39
49,06
20
08/08
5,63
9,24
1,86
-4,76
-0,93
-11,81
-4,64
21
08/09
-14,67
1,54
-12,80
-33,00
-9,91
-15,71
-5,75
22
08/10
-28,91
-27,88
-41,82
-33,21
-13,61
-17,37
-30,05
23
08/11
-12,09
11,34
-16,83
-36,87
3,03
-23,08
-19,46
24
08/12
2,50
7,55
-15,61
1,77
2,35
8,00
-2,50
25
09/01
-10,98
7,02
-7,53
4,35
22,41
-3,09
2,56
26
09/02
-21,92
-8,20
-2,96
2,50
-8,45
-1,27
-10,00
27
09/03
14,04
16,96
9,92
18,70
-1,03
7,74
16,67
28
09/04
43,08
19,85
20,14
37,07
13,99
7,61
43,65
29
09/05
23,66
18,88
9,83
29,90
5,50
20,00
17,68
30
09/06
4,35
31,07
16,14
7,14
12,62
-2,08
9,39
31
09/07
25,83
0,00
12,43
14,07
-7,05
1,06
33,05
32
09/08
21,19
24,14
3,52
22,08
2,23
18,42
7,10
33
09/09
0,00
34,03
3,88
11,17
-2,62
9,33
2,41
34
09/10
21,86
9,33
1,40
-9,09
2,69
5,69
8,24
35
09/11
-8,97
15,17
-6,45
7,37
-3,93
0,00
-15,22
36
09/12
37,93
17,28
20,69
15,69
3,64
14,42
36,54
5,26
102
Dönem Sayısı Dönemler VESTL YKBNK
1
07/01
-4,89
11,38
2
07/02
0,00
11,68
3
07/03
1,14
-3,27
4
07/04
-1,69
1,35
5
07/05
1,15
-0,46
6
07/06
-10,80
-2,01
7
07/07
3,82
32,88
8
07/08
-9,82
-3,61
9
07/09
13,61
3,21
10
07/10
2,99
17,62
11
07/11
-8,14
-3,08
12
07/12
-8,23
-6,36
13
08/01
-34,48
-24,76
14
08/02
7,37
-10,97
15
08/03
-18,63
-6,52
16
08/04
36,14
10,08
17
08/05
-5,31
2,82
18
08/06
-7,94
-23,29
19
08/07
-10,66
38,64
20
08/08
10,23
0,00
21
08/09
-25,77
1,50
22
08/10
-38,19
-28,89
23
08/11
-5,62
-0,52
24
08/12
11,59
9,95
25
09/01
-4,71
-14,76
26
09/02
-1,23
-7,82
27
09/03
1,25
3,64
28
09/04
75,31
26,32
29
09/05
4,23
9,26
30
09/06
2,03
-3,39
31
09/07
10,60
35,09
32
09/08
38,32
2,60
33
09/09
1,73
2,53
34
09/10
0,43
-3,70
35
09/11
-8,05
-6,41
36
09/12
19,82
12,33
103
EK-3 ĠMKB 30 Endeksine Dahil Hisse Senetlerinin Ortalamadan Sapmaları
(Risk-%)
Dönem Sayısı Dönemler AKBNK ARCLK ASYAB BIMAS DOHOL DYHOL ECILC
1
07/01
0,02
0,04
0,13
0,08
0,06
0,00
-0,08
2
07/02
0,01
0,06
-0,03
-0,07
-0,04
-0,04
0,11
3
07/03
0,00
-0,03
0,20
-0,02
0,01
0,09
0,10
4
07/04
0,05
0,07
-0,02
0,02
0,12
0,01
-0,13
5
07/05
-0,10
0,14
-0,08
-0,10
0,10
0,10
0,03
6
07/06
-0,04
-0,03
0,03
0,07
-0,09
-0,05
-0,02
7
07/07
0,19
-0,05
0,08
-0,03
0,06
0,08
-0,11
8
07/08
-0,09
-0,18
-0,07
0,06
-0,12
-0,16
-0,12
9
07/09
0,09
0,05
0,14
0,01
0,06
0,09
0,03
10
07/10
0,13
-0,11
-0,03
-0,07
-0,03
0,14
-0,03
11
07/11
-0,21
-0,10
-0,04
-0,02
-0,11
-0,12
0,01
12
07/12
-0,01
-0,02
0,10
0,04
-0,03
-0,05
-0,04
13
08/01
-0,25
-0,19
-0,14
-0,12
-0,29
-0,26
-0,25
14
08/02
-0,05
0,03
0,15
0,07
-0,02
-0,11
0,13
15
08/03
-0,14
-0,26
-0,30
-0,05
-0,14
-0,26
-0,23
16
08/04
0,16
0,06
0,03
0,07
0,15
0,20
0,05
17
08/05
-0,21
-0,08
-0,09
0,13
-0,08
-0,21
0,01
18
08/06
-0,24
-0,18
-0,32
0,02
0,04
-0,32
-0,03
19
08/07
0,51
0,03
0,26
-0,10
0,16
0,49
0,04
20
08/08
-0,08
0,01
-0,15
0,02
0,00
-0,06
-0,03
21
08/09
0,04
-0,24
-0,25
-0,17
-0,14
-0,25
-0,17
22
08/10
-0,23
-0,41
-0,36
-0,25
-0,19
-0,40
0,03
23
08/11
-0,20
-0,28
-0,10
-0,01
-0,07
-0,23
-0,31
24
08/12
0,09
0,26
-0,10
-0,02
-0,10
-0,02
0,01
25
09/01
-0,02
-0,16
-0,10
0,07
-0,02
-0,03
-0,09
26
09/02
-0,20
-0,03
-0,09
-0,09
-0,18
-0,29
-0,04
27
09/03
0,25
0,04
0,08
0,02
0,07
0,21
0,23
28
09/04
0,25
0,45
0,35
0,21
0,16
0,23
0,18
29
09/05
0,02
0,10
0,16
0,09
0,40
0,64
0,09
30
09/06
0,05
0,05
0,15
0,07
0,24
0,37
0,11
31
09/07
0,18
0,33
0,29
0,04
0,00
-0,01
0,06
32
09/08
0,01
0,35
-0,04
-0,07
0,25
0,27
-0,03
33
09/09
-0,02
-0,02
0,09
0,05
-0,21
-0,34
0,03
34
09/10
-0,07
0,13
-0,01
-0,13
-0,04
-0,01
-0,04
35
09/11
-0,02
0,00
-0,06
0,06
-0,07
0,03
0,18
36
09/12
0,13
0,14
0,12
0,12
0,10
0,28
0,32
104
Dönem Sayısı Dönemler ENKAI EREGL GARAN HALKB ISCTR KCHOL KOZAA
1
07/01
-0,03
0,15
0,10
0,02
0,07
0,14
2
07/02
0,11
0,07
-0,02
-0,01
0,00
-0,21
3
07/03
0,11
0,17
0,12
-0,01
0,00
-0,02
4
07/04
0,06
0,11
0,04
-0,02
0,05
-0,18
5
07/05
0,09
-0,10
0,05
0,04
-0,07
0,05
0,45
6
07/06
-0,02
-0,07
-0,02
-0,05
-0,01
-0,07
0,17
7
07/07
0,06
0,16
0,19
0,03
0,14
0,12
0,09
8
07/08
-0,14
0,05
-0,11
-0,06
-0,12
-0,03
-0,06
9
07/09
0,05
0,08
0,07
0,09
0,14
0,05
0,16
10
07/10
0,17
-0,03
0,12
-0,03
0,08
-0,02
-0,10
11
07/11
0,03
-0,16
-0,06
-0,01
-0,05
-0,08
-0,07
12
07/12
0,05
0,03
-0,03
0,19
-0,05
0,04
0,04
13
08/01
-0,21
-0,32
-0,33
-0,33
-0,22
-0,30
-0,26
14
08/02
0,11
0,17
-0,05
-0,12
-0,04
0,00
-0,14
15
08/03
-0,14
0,05
-0,21
-0,08
-0,14
-0,22
-0,22
16
08/04
0,05
0,18
0,11
-0,04
0,22
0,16
0,03
17
08/05
0,09
-0,06
-0,22
0,05
-0,16
-0,12
-0,18
18
08/06
-0,05
0,26
-0,21
-0,24
-0,22
-0,05
-0,17
19
08/07
-0,05
-0,06
0,35
0,34
0,34
0,37
0,11
20
08/08
-0,24
-0,20
-0,13
-0,20
0,04
-0,13
-0,14
21
08/09
-0,19
-0,21
-0,18
-0,16
-0,07
-0,07
-0,52
22
08/10
-0,36
-0,30
-0,21
-0,30
-0,21
-0,30
-0,40
23
08/11
-0,26
-0,24
-0,13
-0,05
-0,07
-0,13
-0,04
24
08/12
0,19
0,08
0,11
0,09
0,01
0,02
-0,06
25
09/01
0,01
-0,16
-0,17
-0,10
-0,11
-0,14
0,00
26
09/02
0,13
-0,07
-0,12
-0,19
-0,12
-0,10
0,50
27
09/03
-0,07
-0,12
0,10
-0,01
0,13
0,08
0,12
28
09/04
0,14
0,22
0,39
0,51
0,24
0,23
0,08
29
09/05
0,08
0,07
0,11
0,05
0,13
0,18
0,51
30
09/06
-0,05
0,02
0,05
0,00
-0,06
-0,11
0,02
31
09/07
0,02
0,06
0,21
0,26
0,11
0,28
0,00
32
09/08
0,19
0,20
0,03
0,00
0,15
0,13
0,01
33
09/09
0,02
0,05
-0,02
0,06
-0,04
-0,04
0,05
34
09/10
-0,05
-0,13
-0,05
0,00
-0,02
-0,04
0,15
35
09/11
-0,07
-0,05
-0,09
-0,03
-0,11
-0,05
0,21
36
09/12
0,17
0,09
0,19
0,28
0,20
0,16
-0,04
105
Dönem Sayısı Dönemler KRDMD PETKM SAHOL SISE SKBNK TAVHL TCELL
1
07/01
0,22
0,00
0,04
0,10
0,04
0,08
2
07/02
0,06
0,19
-0,04
0,02
0,24
0,03
-0,11
3
07/03
0,15
0,11
-0,02
-0,08
-0,09
0,12
-0,03
4
07/04
-0,03
0,06
0,05
-0,02
0,13
0,01
0,09
5
07/05
0,09
0,16
0,01
0,04
0,29
0,07
0,14
6
07/06
-0,06
-0,02
0,05
0,00
-0,04
-0,07
-0,02
7
07/07
0,24
0,14
0,10
0,08
0,20
0,10
0,01
8
07/08
-0,03
-0,07
-0,03
-0,07
0,17
-0,09
0,01
9
07/09
0,16
-0,01
0,06
0,09
-0,07
-0,02
0,06
10
07/10
-0,07
-0,04
0,01
-0,05
-0,02
-0,03
0,08
11
07/11
-0,02
-0,05
-0,19
-0,11
-0,12
0,04
0,12
12
07/12
0,00
-0,10
-0,04
0,02
0,12
-0,03
-0,02
13
08/01
-0,32
-0,26
-0,26
-0,30
-0,34
-0,24
-0,22
14
08/02
0,17
0,11
0,12
0,14
0,07
-0,05
0,17
15
08/03
-0,16
-0,13
-0,27
-0,14
-0,40
-0,04
-0,10
16
08/04
0,18
0,06
0,13
0,19
0,22
0,23
-0,10
17
08/05
-0,08
0,02
-0,02
-0,15
-0,31
0,19
-0,05
18
08/06
-0,06
-0,33
-0,11
-0,24
0,01
-0,23
-0,29
19
08/07
0,02
0,05
0,37
0,23
0,02
-0,05
0,25
20
08/08
-0,11
0,00
-0,15
-0,01
-0,13
-0,05
-0,13
21
08/09
-0,32
-0,21
-0,05
-0,03
-0,20
-0,12
0,02
22
08/10
-0,37
-0,07
-0,25
-0,22
-0,39
-0,42
-0,10
23
08/11
-0,16
0,14
-0,18
-0,14
-0,18
-0,16
0,14
24
08/12
0,06
-0,06
0,11
0,00
0,00
0,09
-0,03
25
09/01
-0,03
-0,20
-0,11
-0,12
-0,12
0,13
-0,01
26
09/02
-0,03
0,03
-0,24
-0,03
-0,15
-0,02
-0,07
27
09/03
-0,01
0,00
0,15
0,05
0,03
0,05
-0,06
28
09/04
0,34
0,11
0,42
0,24
0,60
0,17
-0,01
29
09/05
0,13
0,19
0,14
0,04
0,10
0,12
0,03
30
09/06
0,01
0,14
-0,08
0,04
-0,03
0,09
0,03
31
09/07
-0,01
0,05
0,31
0,06
0,13
0,01
0,07
32
09/08
0,12
0,01
0,04
0,18
0,27
0,02
0,02
33
09/09
-0,02
0,03
-0,02
-0,01
-0,01
-0,02
0,07
34
09/10
-0,08
-0,04
-0,05
0,00
-0,03
0,02
-0,08
35
09/11
-0,15
-0,13
-0,05
-0,05
-0,13
-0,04
-0,09
36
09/12
0,18
0,11
0,06
0,22
0,10
0,21
0,12
106
Dönem Sayısı Dönemler TEBNK THYAO TKFEN TOASO TTKOM TUPRS VAKBN
1
07/01
-0,06
0,14
0,08
0,01
0,04
2
07/02
0,16
-0,03
-0,03
0,07
-0,07
3
07/03
0,09
-0,12
-0,01
0,12
-0,02
4
07/04
0,04
0,14
0,13
-0,12
0,08
5
07/05
-0,02
-0,06
0,04
0,18
-0,03
6
07/06
0,05
0,09
-0,01
-0,01
-0,09
7
07/07
-0,05
-0,05
-0,03
0,00
0,21
8
07/08
-0,05
-0,12
-0,06
-0,09
-0,14
9
07/09
0,08
-0,02
0,00
0,06
0,08
10
07/10
-0,04
-0,17
0,00
0,01
0,05
11
07/11
-0,08
-0,10
-0,08
-0,09
-0,16
12
07/12
-0,01
0,03
0,06
0,05
0,09
0,05
13
08/01
-0,27
-0,24
-0,02
-0,15
-0,16
-0,33
14
08/02
-0,14
-0,02
-0,01
0,06
0,04
-0,03
15
08/03
-0,33
-0,20
0,01
-0,26
-0,08
-0,18
16
08/04
0,17
0,09
0,18
0,11
0,15
0,04
17
08/05
-0,25
-0,13
0,15
-0,01
-0,01
-0,03
-0,20
18
08/06
-0,20
-0,30
0,01
-0,26
-0,11
-0,09
-0,27
19
08/07
0,33
0,13
-0,16
0,16
0,03
0,10
0,47
20
08/08
0,03
0,04
0,00
-0,06
-0,02
-0,14
-0,07
21
08/09
-0,17
-0,04
-0,14
-0,35
-0,11
-0,18
-0,08
22
08/10
-0,32
-0,33
-0,43
-0,35
-0,14
-0,19
-0,33
23
08/11
-0,15
0,06
-0,18
-0,38
0,02
-0,25
-0,22
24
08/12
0,00
0,02
-0,17
0,00
0,02
0,06
-0,05
25
09/01
-0,14
0,01
-0,09
0,03
0,22
-0,05
0,00
26
09/02
-0,25
-0,14
-0,04
0,01
-0,09
-0,03
-0,13
27
09/03
0,11
0,11
0,09
0,17
-0,02
0,06
0,14
28
09/04
0,40
0,14
0,19
0,35
0,13
0,06
0,41
29
09/05
0,21
0,13
0,08
0,28
0,05
0,18
0,15
30
09/06
0,02
0,26
0,15
0,06
0,12
-0,04
0,07
31
09/07
0,23
-0,06
0,11
0,12
-0,08
-0,01
0,31
32
09/08
0,18
0,19
0,02
0,20
0,02
0,16
0,05
33
09/09
-0,03
0,28
0,03
0,10
-0,03
0,07
0,00
34
09/10
0,19
0,04
0,00
-0,11
0,02
0,04
0,06
35
09/11
-0,12
0,10
-0,08
0,06
-0,05
-0,02
-0,18
36
09/12
0,35
0,12
0,19
0,14
0,03
0,12
0,34
0,04
107
Dönem Sayısı Dönemler VESTL YKBNK
1
07/01
-0,06
0,09
2
07/02
-0,01
0,09
3
07/03
0,00
-0,06
4
07/04
-0,03
-0,01
5
07/05
0,00
-0,03
6
07/06
-0,12
-0,04
7
07/07
0,03
0,31
8
07/08
-0,11
-0,06
9
07/09
0,13
0,01
10
07/10
0,02
0,15
11
07/11
-0,09
-0,05
12
07/12
-0,09
-0,09
13
08/01
-0,36
-0,27
14
08/02
0,06
-0,13
15
08/03
-0,20
-0,09
16
08/04
0,35
0,08
17
08/05
-0,06
0,01
18
08/06
-0,09
-0,26
19
08/07
-0,12
0,36
20
08/08
0,09
-0,02
21
08/09
-0,27
-0,01
22
08/10
-0,39
-0,31
23
08/11
-0,07
-0,03
24
08/12
0,11
0,08
25
09/01
-0,06
-0,17
26
09/02
-0,02
-0,10
27
09/03
0,00
0,01
28
09/04
0,74
0,24
29
09/05
0,03
0,07
30
09/06
0,01
-0,06
31
09/07
0,10
0,33
32
09/08
0,37
0,00
33
09/09
0,01
0,00
34
09/10
-0,01
-0,06
35
09/11
-0,09
-0,09
36
09/12
0,19
0,10
108
EK-4 Son Dört Çeyrek Net Kar Değerleri Kullanılarak Hesaplanan HBK,
F/K ve Sektörel F/K Oranları
AKBNK- AKBANK T. A.ġ
Dönemler
(Yıl)
2007
2008
2009
Hisse BaĢına Kar
(HBK)
0,66
0,57
0,91
Fiyat/Kazanç
(F/K)
13,09
8,41
10,4
Sektörel Fiyat/Kazanç
(F/K)
12,86
6,75
11,29
ARCLK-ARÇELĠK A.ġ.
Dönemler
(Yıl)
2007
2008
2009
Hisse BaĢına Kar
(HBK)
0,39
0,02
0,74
Fiyat/Kazanç
(F/K)
20,66
125,67
7,86
Sektörel Fiyat/Kazanç
(F/K)
16,09
5,52
22,95
ASYAB-ASYA KATILIM BANKASI A.ġ.
Dönemler
(Yıl)
2007
2008
2009
Hisse BaĢına Kar
(HBK)
0,74
0,27
0,33
Fiyat/Kazanç
(F/K)
14,91
4,23
10,34
Sektörel Fiyat/Kazanç
(F/K)
12,86
6,75
11,29
109
BIMAS - BĠM BĠRLEġĠK MAĞAZALAR A.ġ.
Dönemler
(Yıl)
2007
2008
2009
Hisse BaĢına Kar
(HBK)
4,29
1,5
2,81
Fiyat/Kazanç
(F/K)
24,49
21,44
24,77
Sektörel Fiyat/Kazanç
(F/K)
56,04
5,94
37,91
DOHOL-DOĞAN HOLDĠNG
Dönemler
(Yıl)
2007
2008
2009
Hisse BaĢına Kar
(HBK)
0,26
-0,05
-0,13
Fiyat/Kazanç
(F/K)
8,43
-
Sektörel Fiyat/Kazanç
(F/K)
8,05
3,36
19,63
DYHOL-DOĞAN YAYIN HOLDĠNG A.ġ.
Dönemler
(Yıl/Ay)
07/12
08/12
09/12
Hisse BaĢına Kar
(HBK)
1
-0,63
-0,56
Fiyat/Kazanç
(F/K)
4,77
-
Sektörel Fiyat/Kazanç
(F/K)
8,05
3,36
19,63
ECILC-EĠS ECZACIBAġI ĠLAÇ, SINAĠ VE FĠNANSAL YATIRIMLAR
SAN VE TĠC. A.ġ
Dönemler
(Yıl/Ay)
07/12
08/12
09/12
Hisse BaĢına Kar
(HBK)
2,47
0,13
0,53
Fiyat/Kazanç
(F/K)
2,1
6,74
4,69
Sektörel Fiyat/Kazanç
(F/K)
6,66
4,02
135,87
110
ENKAI-ENKA ĠNġAAT A.ġ.
Dönemler
(Yıl/Ay)
07/12
08/12
09/12
Hisse BaĢına Kar
(HBK)
0,83
0,72
0,48
Fiyat/Kazanç
(F/K)
24,7
7,33
14,27
Sektörel Fiyat/Kazanç
(F/K)
25,91
6,97
19,14
EREGL-EREĞLĠ DEMĠR VE ÇELĠK FABRĠKALARI T. A.ġ.
Dönemler
(Yıl/Ay)
07/12
08/12
09/12
Hisse BaĢına Kar
(HBK)
0,8
0,2
-0,11
Fiyat/Kazanç
(F/K)
12,8
20,79
-
Sektörel Fiyat/Kazanç
(F/K)
9,61
2,81
*
GARAN-T. GARANTĠ BANKASI A.ġ.
Dönemler
(Yıl/Ay)
07/12
08/12
09/12
Hisse BaĢına Kar
(HBK)
1,1
0,42
0,71
Fiyat/Kazanç
(F/K)
9,52
6,24
9
Sektörel Fiyat/Kazanç
(F/K)
12,86
6,75
11,29
HALKB-TÜRKĠYE HALK BANKASI A.ġ.
Dönemler
(Yıl/Ay)
07/12
08/12
09/12
Hisse BaĢına Kar
(HBK)
0,9
0,81
1,3
Fiyat/Kazanç
(F/K)
13,48
5,65
9,12
Sektörel Fiyat/Kazanç
(F/K)
12,86
6,75
11,29
111
ISCTR-T. Ġġ BANKASI A.ġ.
Dönemler
(Yıl/Ay)
07/12
08/12
09/12
Hisse BaĢına Kar
(HBK)
0,62
0,55
0,77
Fiyat/Kazanç
(F/K)
11,91
7,49
8,18
Sektörel Fiyat/Kazanç
(F/K)
12,86
6,75
11,29
KCHOL-KOÇ HOLDĠNG A.ġ.
Dönemler
(Yıl/Ay)
07/12
08/12
09/12
Hisse BaĢına Kar
(HBK)
1,31
1,28
1,09
Fiyat/Kazanç
(F/K)
4,83
2,05
4,04
Sektörel Fiyat/Kazanç
(F/K)
8,05
3,36
19,63
KOZAA-KOZA DAVETĠYE MAĞAZA ĠġLETMELERĠ VE ĠHRACAT A.ġ.
Dönemler
(Yıl/Ay)
07/12
08/12
09/12
Hisse BaĢına Kar
(HBK)
0,59
0,22
0,62
Fiyat/Kazanç
(F/K)
17,74
4,02
7,81
Sektörel Fiyat/Kazanç
(F/K)
16,63
18,32
*
KRDMD-KARDEMĠR KARABÜK DEMĠR ÇELĠK SAN. VE TĠC. A.ġ.
Dönemler
(Yıl/Ay)
07/12
08/12
09/12
Hisse BaĢına Kar
(HBK)
0,23
0,47
-0,08
Fiyat/Kazanç
(F/K)
6,09
1,07
-
Sektörel Fiyat/Kazanç
(F/K)
9,61
2,81
*
112
PETKM-PETKĠM PETROKĠMYA HOLDĠNG A.ġ.
Dönemler
(Yıl/Ay)
07/12
08/12
09/12
Hisse BaĢına Kar
(HBK)
0,36
-0,74
0,56
Fiyat/Kazanç
(F/K)
23,84
13,11
Sektörel Fiyat/Kazanç
(F/K)
6,66
4,02
135,87
SAHOL-H.Ö SABANCI HOLDĠNG A.ġ
Dönemler
(Yıl/Ay)
07/12
08/12
09/12
Hisse BaĢına Kar
(HBK)
0,54
1,29
1,6
Fiyat/Kazanç
(F/K)
11,98
2,71
3,59
Sektörel Fiyat/Kazanç
(F/K)
8,05
3,36
19,63
SISE-ġĠġE CAM
Dönemler
(Yıl/Ay)
07/12
08/12
09/12
Hisse BaĢına Kar
(HBK)
0,29
0,19
0,11
Fiyat/Kazanç
(F/K)
8,06
5,81
17,28
Sektörel Fiyat/Kazanç
(F/K)
8,05
3,36
19,63
SKBNK-ġEKERBANK
Dönemler
(Yıl/Ay)
07/12
08/12
09/12
Hisse BaĢına Kar
(HBK)
0,31
0,36
0,3
Fiyat/Kazanç
(F/K)
16,93
3,02
8,46
Sektörel Fiyat/Kazanç
(F/K)
12,86
6,75
11,29
113
TAVHL-TAV HAVALĠMANLARI HOLDĠNG A.ġ.
Dönemler
(Yıl/Ay)
07/12
08/12
09/12
Hisse BaĢına Kar
(HBK)
-0,28
0,04
0,3
Fiyat/Kazanç
(F/K)
91,36
15,56
Sektörel Fiyat/Kazanç
(F/K)
8,05
3,36
19,63
TCELL-TURKCELL ĠLETĠġĠM ĠġLETMELERĠ A.ġ.
Dönemler
(Yıl/Ay)
07/12
08/12
09/12
Hisse BaĢına Kar
(HBK)
0,8
1
0,79
Fiyat/Kazanç
(F/K)
16,01
8,78
13,45
Sektörel Fiyat/Kazanç
(F/K)
16,61
6,65
11,67
TEBNK-TÜRK EKONOMĠ BANKASI A.ġ.
Dönemler
(Yıl/Ay)
07/12
08/12
09/12
Hisse BaĢına Kar
(HBK)
0,17
0,15
0,19
Fiyat/Kazanç
(F/K)
17,04
5,49
14,66
Sektörel Fiyat/Kazanç
(F/K)
12,86
6,75
11,29
THYAO-TÜRK HAVAYOLLARI A.O.
Dönemler
(Yıl/Ay)
07/12
08/12
09/12
Hisse BaĢına Kar
(HBK)
1,67
6,48
0,64
Fiyat/Kazanç
(F/K)
5,16
0,88
8,92
Sektörel Fiyat/Kazanç
(F/K)
6,23
1,55
5,75
114
TKFEN-TEKFEN HOLDĠNG A.ġ.
Dönemler
(Yıl/Ay)
07/12
08/12
09/12
Hisse BaĢına Kar
(HBK)
0,94
0,31
0,19
Fiyat/Kazanç
(F/K)
6,85
9,54
26,22
Sektörel Fiyat/Kazanç
(F/K)
8,05
3,36
19,63
TOASO-TOFAġ TÜRK OTOMOBĠL FABRĠKASI A.ġ.
Dönemler
(Yıl/Ay)
07/12
08/12
09/12
Hisse BaĢına Kar
(HBK)
0,35
0,35
0,72
Fiyat/Kazanç
(F/K)
17,49
3,27
6,55
Sektörel Fiyat/Kazanç
(F/K)
16,09
5,52
22,95
TTKOM-TÜRK TELEKOMÜNĠKASYON A.ġ.
Dönemler
(Yıl/Ay)
07/12
08/12
09/12
Hisse BaĢına Kar
(HBK)
0,73
0,46
0,47
Fiyat/Kazanç
(F/K)
7,48
9,66
Sektörel Fiyat/Kazanç
(F/K)
16,61
6,65
11,67
TUPRS-TÜPRAġ TÜRKĠYE PETROL RAFĠNELERĠ A.ġ.
Dönemler
(Yıl/Ay)
07/12
08/12
09/12
Hisse BaĢına Kar
(HBK)
5,18
1,75
3,26
Fiyat/Kazanç
(F/K)
6,61
9,23
9,13
Sektörel Fiyat/Kazanç
(F/K)
6,66
4,02
135,87
115
VAKBN-TÜRKĠYE VAKIFLAR BANKASI T.A.O.
Dönemler
(Yıl/Ay)
07/12
08/12
09/12
Hisse BaĢına Kar
(HBK)
0,41
0,3
0,5
Fiyat/Kazanç
(F/K)
10,04
3,88
8,51
Sektörel Fiyat/Kazanç
(F/K)
12,86
6,75
11,29
VESTL-VESTEL ELEKTRONĠK SANAYĠ VE TĠCARET A.ġ.
Dönemler
(Yıl/Ay)
07/12
08/12
09/12
Hisse BaĢına Kar
(HBK)
0,11
-2,28
0,3
Fiyat/Kazanç
(F/K)
25,61
8,66
Sektörel Fiyat/Kazanç
(F/K)
16,09
5,52
22,95
YKBNK-YAPI VE KREDĠ BANKASI A.ġ.
Dönemler
(Yıl/Ay)
07/12
08/12
09/12
Hisse BaĢına Kar
(HBK)
0,21
0,24
0,31
Fiyat/Kazanç
(F/K)
19,91
8,76
10,52
Sektörel Fiyat/Kazanç
(F/K)
12,86
6,75
11,29
(-) Hisse senedinin zarar etmesi dolayısıyla F/K oranı hesaplanmamıĢtır
* Sektörün zarar etmesi dolayısıyla F/K oranı hesaplanmamıĢtır
116
EK-5 ĠMKB 30 Endeksine Dahil Olan Hisselerin ADI (Topalama-Dağıtım
Endeksi) Değerleri
AKBNK- AKBANK T. A.Ş
Dönem
En Düşük En Yüksek Kapanış
Sayısı Dönemler
Fiyat
Fiyat
Fiyatı
(Yıl/Ay)
(TL)
(TL)
(TL)
Toplam İşlem
Miktarı
(Adet)
ADI
1
2
07/01
07/02
8,15
9,1
9,8
10,2
9
9,3
79961994
79741683
0
-48321616,64
3
4
07/03
07/04
8,65
9,15
9,55
10,7
9,3
10
72185881
53866875
-16239002,86
-11026079,47
5
6
07/05
07/06
9
7,05
10
9,4
9,25
7,3
74505079
52889216
-48278618,97
-89914810,29
7
8
07/07
07/08
7,25
7,1
10,15
8,7
8,85
8,3
145351552
170993633
-74878442,84
10618373,66
9
10
07/09
07/10
7,9
9
9,95
11,2
9,2
10,6
119883169
135016310
42782150,71
104153200,7
11
12
07/11
07/12
8,1
8,4
11,2
9,25
8,6
8,7
250771862
150400090
-65724512,26
-109959832,8
13
08/01
6,6
8,7
6,75
231696668
14
15
08/02
08/03
6,4
5,45
7,5
6,55
6,55
5,6
163390273
216942721
-317426433,5
-475202957,8
16
17
08/04
08/05
5,5
5,15
6,9
6,75
6,65
5,4
288892034
164055089
-289486650,2
-402274523,9
18
19
08/06
08/07
4,22
3,9
5,8
7,1
4,24
6,5
180527538
223918267
-578231744,5
-438282827,6
20
21
08/08
08/09
5,7
4,6
7
6,65
6,15
6,55
143367416
241837490
-482395878,7
-264152290,2
22
23
08/10
08/11
4,04
3,36
6,2
5,3
5,22
4,3
276311980
322847298
-238567847,6
-248552815,6
24
08/12
3,72
5,18
4,78
199140943
-158530197,5
25
26
09/01
09/02
4,06
3,62
5,15
5,02
4,78
3,92
256733492
308276057
0
-93720387,04
27
28
09/03
09/04
3,42
4,88
4,92
6,40
4,88
6,20
268600324
228470007
160554586,3
328900907,3
29
30
09/05
09/06
5,70
5,85
6,90
7,35
6,45
6,90
173119207
153532846
372180709
433593847,4
31
32
09/07
09/08
6,80
7,70
8,65
9,20
8,30
8,60
146495054
161979034
524658340,5
557054147,3
33
34
09/09
09/10
7,95
8,1
8,8
9,85
8,6
8,2
135321609
183828425
628694999,1
465875537
35
36
09/11
09/12
7,9
8,15
8,8
9,75
8,2
9,45
133674927
107138540
421317228
488278815,5
0
117
ARCLK-ARÇELİK A.Ş.
Dönem
En Düşük En Yüksek Kapanış
Sayısı Dönemler
Fiyat
Fiyat
Fiyatı
(Yıl/Ay)
(TL)
(TL)
(TL)
Toplam İşlem
Miktarı
(Adet)
ADI
0
1
07/01
8,15
9,2
8,85
24101291
2
3
07/02
07/03
8,95
8,75
10,5
9,85
9,55
9,4
18118710
14539669
3942442,054
6586018,236
4
5
07/04
07/05
9,25
9,85
11,2
12,3
10,2
11,4
14670033
11615632
6209863,543
9291561,829
6
7
07/06
07/07
10,3
10,3
11,4
12,1
11,3
10,9
4011917
10565974
12574039,37
9052048,041
8
9
07/08
07/09
8,25
8,95
10,8
10,25
9,15
9,8
18057832
21118889
3740920,982
10239040,67
10
11
07/10
07/11
8,65
7,55
10,4
9,1
8,9
8,2
18847102
23289225
-3223175,04
-6979501,653
12
07/12
7,6
8,45
8,15
15447213
-2436203,711
13
14
08/01
08/02
6,45
6,5
8,1
7,4
6,7
7
16149979
14141811
0
-9684733,636
15
16
08/03
08/04
5,1
5,1
6,95
5,9
5,3
5,7
18170874
38694777
-23926770,01
-4579381,515
17
18
08/05
08/06
5,05
4,08
5,95
5,15
5,1
4,28
10959635
12026170
-14321279,29
-21851684,81
19
20
08/07
08/08
3,8
4,44
4,64
5,04
4,48
4,62
19685838
13820374
-9665213,664
-15193363,26
21
22
08/09
08/10
3,54
1,94
4,68
3,58
3,6
2,19
16587147
13827728
-30034494,79
-39646452,06
23
24
08/11
08/12
1,38
1,44
2,35
2,19
1,61
2,06
100528399
129984318
-92501589,68
-7578501,917
25
09/01
1,66
2,12
1,76
114058373
26
27
09/02
09/03
1,59
1,58
1,85
1,91
1,74
1,83
152280098
131311216
-41040068,66
26605103,22
28
29
09/04
09/05
1,82
2,06
2,96
2,57
2,68
2,19
125189868
250525165
90298193,96
-32508259,47
30
31
09/06
09/07
2,17
2,26
2,48
3,20
2,33
3,14
364533515
533492226
-20749113,83
444637721,6
32
33
09/08
09/09
3,18
4,02
4,78
4,56
4,30
4,3
415311184
170893260
610762195,2
617091575,2
34
35
09/10
09/11
4,14
4,02
5,14
5,16
4,95
5,05
285868275
298846888
794329905,7
1035504587
36
09/12
5
6,1
5,85
90967084
1085122997
0
118
ASYAB-ASYA KATILIM BANKASI A.Ş.
Dönem
Sayısı
Dönemler
(Yıl/Ay)
En Düşük En Yüksek Kapanış
Fiyat
Fiyat
Fiyatı
(TL)
(TL)
(TL)
Toplam İşlem
Miktarı
(Adet)
ADI
0
1
07/01
4,95
6,8
6,5
35129988
2
3
07/02
07/03
6,3
6,15
6,75
8,05
6,5
7,95
33135572
26918103
20054748,16
44139366,63
4
5
07/04
07/05
7,1
6,9
8,55
8,1
8
7,6
15781762
17928107
47948757,46
50936775,29
6
7
07/06
07/07
6,55
7,9
8,4
9,5
8,05
8,9
36304174
28605020
73504234,8
80655489,8
8
9
07/08
07/09
7,65
8,5
8,8
9,9
8,5
9,9
12532759
12433076
86649418,02
99082494,02
10
11
07/10
07/11
9,2
8,85
10,1
9,95
9,9
9,8
7668498
13037422
103342770,7
112824532,1
12
07/12
9,7
12
11
10527446
114197677,3
13
14
08/01
08/02
9
9,4
12,1
11,9
9,8
11,5
24481790
10761407
0
-4528270,659
15
16
08/03
08/04
8,35
8,25
11,3
9,2
8,35
8,85
19611592
13541495
-24139862,66
-20576311,34
17
18
08/05
08/06
7,6
2,24
9,25
8,5
8,3
2,3
18094648
27053029
-23317924,68
-49852365,26
19
20
08/07
08/08
2,04
2,6
3,06
3,08
2,96
2,6
89880453
48825709
22404469,5
-26421239,5
21
22
08/09
08/10
1,85
1,04
2,64
1,91
2,02
1,35
152248988
367203440
-113145346,6
-218663576,5
23
24
08/11
08/12
1,02
1,1
1,62
1,25
1,25
1,16
370773019
206115052
-305177280,9
-346400291,3
25
09/01
1,02
1,31
1,07
289162955
26
27
09/02
09/03
0,95
0,94
1,09
1,15
1
1,11
254480602
250182238
-262160334,6
-107285615,9
28
29
09/04
09/05
1,1
1,51
1,55
1,99
1,53
1,82
463005014
442417832
314563396,9
443601931,2
30
31
09/06
09/07
1,79
2,11
2,17
2,88
2,14
2,82
232140228
210825331
639088439
817057874,3
32
33
09/08
09/09
2,46
2,64
3,08
3,26
2,78
3,1
180414133
134521577
822877685
887968770,7
34
35
09/10
09/11
3
2,84
3,68
3,3
3,14
3,02
206960966
173708075
766227025,9
728464400,9
36
09/12
2,98
3,56
3,46
177139936
844521600,4
0
119
BIMAS - BİM BİRLEŞİK MAĞAZALAR A.Ş.
Dönem
Sayısı
Dönemler
(Yıl/Ay)
En Düşük En Yüksek Kapanış
Fiyat
Fiyat
Fiyatı
(TL)
(TL)
(TL)
Toplam İşlem
Miktarı
(Adet)
ADI
0
1
07/01
73
87
83,5
284478
2
3
07/02
07/03
78
71
90
85,5
80,5
79,5
289639
333016
-26717,08333
30699,46839
4
5
07/04
07/05
77,5
75,5
88,5
87,5
86,5
79
330531
668154
241037,3775
-37360,12252
6
7
07/06
07/07
75,5
82
87
95
87
87,5
318614
410777
281253,8775
218057,4159
8
9
07/08
07/09
83,5
95
105,5
107
95,5
100
1212722
559328
328304,8705
235083,5372
10
11
07/10
07/11
92
93
101,5
101,5
96
97,5
919225
423824
89942,74768
114873,5712
12
07/12
97,5
117
105
431038
15403,26352
13
14
08/01
08/02
91
91,5
110
116
96,5
107
266069
286362
0
-36055,46079
15
16
08/03
08/04
104
99
121
118
105
116
218925
241229
-229224,5784
-38780,63107
17
18
08/05
08/06
115
41,5
137
146
133
46,75
852179
623252
503515,0962
-57113,4971
19
20
08/07
08/08
37,5
44
46,5
55,5
43,75
46
1301409
1577732
448990,0029
-579965,6493
21
22
08/09
08/10
34
29,5
46,75
41
39,75
31
1648916
3701963
-741624,0806
-3477857,602
23
24
08/11
08/12
19,1
30
33,5
34,5
31,75
32,25
5273171
2095863
513639,8907
513639,8907
25
09/01
31,50
38,50
35,50
2371574
26
27
09/02
09/03
32,25
30,00
38,50
36,75
33,50
35,25
1749123
3192186
-710677,5143
1062759,152
28
29
09/04
09/05
33,25
41,50
44,25
48,75
44,00
48,75
3200347
3489480
4117635,834
7607115,834
30
31
09/06
09/07
44,75
51,50
56,00
62,00
54,00
58,00
3959103
2841341
10158537,77
10835047,53
32
33
09/08
09/09
53,50
53
61,50
62,5
56,00
60,5
4550661
3365942
9128549,654
11077252,92
34
35
09/10
09/11
53,5
53,5
64
62
55
60
3643311
2625975
8474887,918
9865109,976
36
09/12
60
74,5
69,5
2768174
10724198,46
0
120
DOHOL-DOĞAN HOLDİNG
Dönem
En Düşük En Yüksek Kapanış
Sayısı Dönemler
Fiyat
Fiyat
Fiyatı
(Yıl/Ay)
(TL)
(TL)
(TL)
Toplam İşlem
Miktarı
(Adet)
ADI
1
2
07/01
07/02
1,92
2,2
2,64
2,6
2,37
2,29
938323619
813256131
0
-212709967,3
3
4
07/03
07/04
2,04
2,31
2,37
2,84
2,32
2,6
736176825
626734968
300382971,3
359508911,7
5
6
07/05
07/06
2,46
2,56
2,92
2,88
2,88
2,64
347113676
104054563
646254991,9
594227710,4
7
8
07/07
07/08
2,64
2,26
3,16
2,74
2,82
2,49
806592728
382878862
346045332,5
330092046,6
9
10
07/09
07/10
2,42
2,26
2,76
2,7
2,64
2,56
343290083
825411736
431059718,1
731209440,3
11
12
07/11
07/12
2,18
2,16
2,6
2,35
2,29
2,22
458769358
274827167
512747841,2
411495727,1
13
08/01
1,55
2,22
1,58
485246497
14
15
08/02
08/03
1,44
1,3
1,83
1,55
1,55
1,34
495729616
291381112
-657878855,3
-856018011,5
16
17
08/04
08/05
1,32
1,35
1,67
1,59
1,55
1,43
351127320
219663833
-745663710,9
-818884988,6
18
19
08/06
08/07
1,42
1,18
1,71
1,74
1,49
1,73
288727380
283189902
-968226736,9
-695150759,9
20
21
08/08
08/09
1,7
1,33
1,88
1,79
1,73
1,5
193382412
111756487
-824072367,9
-853226234,1
22
23
08/10
08/11
0,96
1,01
1,5
1,32
1,22
1,14
125931985
123757258
-857890381,7
-877851229,8
24
08/12
0,99
1,13
1,03
70092870
-907891031,2
25
26
09/01
09/02
0,52
0,46
0,72
0,68
0,62
0,51
289299875
193957068
0
-105794764,4
27
28
09/03
09/04
0,41
0,54
0,55
0,68
0,55
0,64
215634278
386579333
109839513,6
275516370,6
29
30
09/05
09/06
0,65
0,87
0,93
1,16
0,90
1,12
510117639
850108838
676323087
1291919142
31
32
09/07
09/08
1,01
1,10
1,22
1,50
1,12
1,41
1089864099
1398706409
1343817433
2113105957
33
34
09/09
09/10
0,99
0,91
1,43
1,19
1,12
1
902760040
790746748
1743795032
1461385479
35
36
09/11
09/12
0,88
0,9
1,12
1,08
0,93
1,03
626876096
533857867
1095707756
1332977920
0
121
DYHOL-DOĞAN YAYIN HOLDİNG A.Ş.
Dönem
En Düşük En Yüksek Kapanış
Sayısı Dönemler
Fiyat
Fiyat
Fiyatı
(Yıl/Ay)
(TL)
(TL)
(TL)
Toplam İşlem
Miktarı
(Adet)
ADI
1
2
07/01
07/02
4
4,52
5,2
5,4
4,95
4,72
141083747
101389685
0
26995387,87
3
4
07/03
07/04
4,34
4,95
5,3
5,65
5,1
5,1
75100394
54483126
70803951,04
39670736,18
5
6
07/05
07/06
4,84
4,95
5,7
5,6
5,6
5,3
62475629
20746722
87617149,13
89213050,83
7
8
07/07
07/08
5,2
4,26
6,1
5,75
5,7
4,6
45378977
43646795
94255159,38
70527707,07
9
10
07/09
07/10
4,64
4,7
5,2
5,95
5,15
5,85
71070508
55835244
128907052,9
175808657,9
11
12
07/11
07/12
4,85
4,7
6,1
5,15
5,1
4,76
24759259
23120967
160953102,5
143997726,7
13
08/01
3,46
4,76
3,52
26568496
14
15
08/02
08/03
2,98
2,2
3,76
3,06
3,12
2,28
68778411
69827176
-68204744,45
-125040817,9
16
17
08/04
08/05
2,24
2,06
3,04
2,74
2,72
2,13
69119564
61803022
-111216905,1
-160295775,5
18
19
08/06
08/07
1,43
1,17
2,23
2,13
1,43
2,12
186848870
228967266
-347144645,5
-122947530,9
20
21
08/08
08/09
1,92
1,3
2,36
2,05
1,99
1,49
109528618
65193607
-197626134,1
-229788313,6
22
23
08/10
08/11
0,78
0,6
1,46
1,03
0,89
0,68
138623354
335858705
-323562935,4
-534450959,4
24
08/12
0,59
0,7
0,66
170519299
-487945696,1
25
26
09/01
09/02
0,6
0,43
0,82
0,67
0,64
0,45
207416504
151187520
0
-257981920,7
27
28
09/03
09/04
0,43
0,53
0,55
0,7
0,54
0,66
126194808
188968785
-152819580,7
-52777282,79
29
30
09/05
09/06
0,67
1,05
1,13
1,64
1,08
1,47
361127460
317004633
229844207,6
364168204,7
31
32
09/07
09/08
1,27
1,37
1,7
1,79
1,45
1,64
686372165
769185401
252433201,1
472200458,5
33
34
09/09
09/10
1
0,93
1,69
1,24
1,08
1,06
828223954
490608359
-163971564,1
-243101944,6
35
36
09/11
09/12
1,04
1,04
1,49
1,46
1,09
1,39
701562594
573503768
-788761739,9
-406425894,6
0
122
ECILC-EİS ECZACIBAŞI İLAÇ, SINAİ VE FİNANSAL YATIRIMLAR SANAYİ VE
TİCARET A.Ş.
Dönem
Sayısı
Dönemler
(Yıl/Ay)
En Düşük En Yüksek
Fiyat
Fiyat
(TL)
(TL)
Kapanış
Fiyatı
(TL)
Toplam İşlem
Miktarı
(Adet)
ADI
1
2
07/01
07/02
4,65
5,15
5,55
6
5,1
5,75
22948625
18379650
0
7568091,176
3
4
07/03
07/04
5,4
5,5
7,1
6,95
6,45
5,75
89967574
35950386
28736932,12
5183230,945
5
6
07/05
07/06
5,5
5,55
6,45
6,2
6,05
6,05
21507999
18819594
8579230,787
18712858,33
7
8
07/07
07/08
5,35
4,48
6,3
5,4
5,5
4,86
31495629
32769088
-2836782,569
-8535754,395
9
10
07/09
07/10
4,92
4,85
5,35
5,65
5,2
5,15
51204881
28890815
6944791,024
-277912,7264
11
12
07/11
07/12
4,9
5,15
5,45
5,65
5,3
5,2
25272580
19475651
11209623,64
-4370897,163
13
08/01
3,8
5,35
3,98
13817443
14
15
08/02
08/03
3,96
3,56
4,66
4,48
4,56
3,62
26309026
13721620
8183930,996
-3747912,482
16
17
08/04
08/05
3,58
3,72
4,04
4,08
3,88
3,86
44747328
30404658
9870839,518
3114248,851
18
19
08/06
08/07
3,78
3,52
4,38
4,08
3,84
4,08
20603798
23174480
-13368789,55
9805690,451
20
21
08/08
08/09
1,32
1,01
4,28
1,37
1,35
1,15
41950988
28612907
-31294939,68
-37653363,46
22
23
08/10
08/11
1,03
0,74
1,36
1,27
1,21
0,86
38450328
34366018
-34157879,1
-52961926,68
24
08/12
0,78
0,92
0,89
52874831
-22747737,54
25
26
09/01
09/02
0,79
0,79
0,95
0,86
0,83
0,81
75208382
41853221
0
-55541285,71
27
28
09/03
09/04
0,79
0,99
1,02
1,24
1,01
1,21
115900683
144749810
50281077,02
160290932,6
29
30
09/05
09/06
1,08
1,22
1,3
1,49
1,25
1,41
152844345
131200179
243660575,4
297112500,1
31
32
09/07
09/08
1,34
1,46
1,68
1,64
1,53
1,51
161914171
196428609
316161226,1
228859622,1
33
34
09/09
09/10
1,41
1,54
1,67
1,77
1,59
1,56
150655725
204173853
286804131,7
118138774,9
35
36
09/11
09/12
1,46
1,87
1,88
2,64
1,87
2,5
334343975
886818062
436561608,3
1000900375
0
123
ENKAI-ENKA İNŞAAT A.Ş.
Dönem
Sayısı
Dönemler
(Yıl/Ay)
En Düşük En Yüksek
Fiyat
Fiyat
(TL)
(TL)
Kapanış Toplam İşlem
Fiyatı
Miktarı
(TL)
(Adet)
ADI
1
2
07/01
07/02
14,4
14,5
16,1
16,9
14,9
16,8
2796911
3964265
0
2482240,348
3
4
07/03
07/04
15,7
18,3
18,9
22,7
18,9
20,4
5747913
4347623
8230153,348
8032534,121
5
6
07/05
07/06
14,7
13,5
23,3
16
15
15
1675505
3409502
6473924,818
7155825,218
7
8
07/07
07/08
14,7
12
16,7
16,1
16,2
14,3
5570713
5496562
9941181,718
10611494,16
9
10
07/09
07/10
13,7
15,1
15,3
18,2
15,3
18,2
6141409
4863689
16752903,16
21616592,16
11
12
07/11
07/12
17,3
18
20,4
20,6
19,1
20,5
4928108
3439748
22411448,29
25586600,29
13
08/01
15,8
20,7
16,5
5218786
14
15
08/02
08/03
15,9
16
19,7
19,3
18,6
16,4
5773985
5419696
-1296552,707
-5402383,01
16
17
08/04
08/05
16,2
12,3
18,6
18,5
17,6
14,6
3218280
8463624
-4866003,01
-7050164,042
18
19
08/06
08/07
13,5
12,4
15,9
14,8
14,1
13,6
6553808
8052725
-10327068,04
-10327068,04
20
21
08/08
08/09
10,4
7,7
15
11,2
10,6
8,75
11368037
21492268
-20706580,09
-29303487,29
22
23
08/10
08/11
5,35
3,54
8,1
6,4
5,75
4,34
27390115
47445510
-48725568,83
-69628136,17
24
08/12
3,72
5,85
5,25
32681697
-55358662,84
25
26
09/01
09/02
4,95
5,3
5,65
6,95
5,4
6,2
25695319
22913771
0
9424589,805
27
28
09/03
09/04
5
5,8
6,45
7
5,9
6,85
34506849
29485624
17753829,22
39868047,22
29
30
09/05
09/06
6,8
4,64
8,3
5,4
7,45
4,82
35654631
82443558
35114096,42
-8277249,897
31
32
09/07
09/08
4,54
5
5,2
6,65
5
6,05
81063505
96164066
23656858,13
49883421,59
33
34
09/09
09/10
5,55
5,55
6,45
6,6
6,3
6,1
58151160
99961341
88650861,59
93410925,45
35
36
09/11
09/12
5,65
5,65
6,45
7
5,8
6,9
54122497
67214624
59584364,82
116841266,7
0
124
EREGL-EREĞLİ DEMİR VE ÇELİK FABRİKALARI T. A.Ş.
Dönem
En Düşük En Yüksek Kapanış
Sayısı Dönemler
Fiyat
Fiyat
Fiyatı
(Yıl/Ay)
(TL)
(TL)
(TL)
Toplam İşlem
Miktarı
(Adet)
ADI
0
1
07/01
8,4
10,8
10,6
25768145
2
3
07/02
07/03
9,9
10,9
14
14
11,6
13,9
34966316
32785721
15503595,34
46174108,53
4
5
07/04
07/05
13,6
8,1
15,8
16
15,8
8,4
15940835
15281238
62114943,53
47994305,89
6
7
07/06
07/07
7,35
7,85
8,55
10,4
8
9,5
19890072
45868767
49651811,89
63142625,71
8
9
07/08
07/09
8,45
9,9
10,3
12
10,2
11,3
26045615
14450535
86372498,55
91189343,55
10
11
07/10
07/11
9,9
9,55
11,9
11,5
11,3
9,75
22266811
12546218
100096067,9
90123433,13
12
07/12
9,5
10,9
10,3
15806879
92381558,7
13
14
08/01
08/02
7,1
6,85
10,3
9,1
7,3
8,7
25974353
34454782
0
-523366,0306
15
16
08/03
08/04
8,25
9,25
9,8
11,4
9,35
11,3
32656160
24940313
13171152,68
35791436,56
17
18
08/05
08/06
7,6
7,7
12,6
10,8
7,8
10
27457077
49026839
10530925,72
34253589,76
19
20
08/07
08/08
8,45
7,9
10
10,2
9,65
8
49058543
59103704
61156661,72
7192410,245
21
22
08/09
08/10
5,05
3,54
7,9
6,1
6,5
4,74
115575265
103850468
9220046,473
2729392,223
23
24
08/11
08/12
2,94
3,28
4,94
4,3
3,72
4,12
112411569
79544661
-22001152,96
29468921,81
25
09/01
3,34
4,56
3,58
117562404
26
27
09/02
09/03
3,32
2,72
4,08
3,54
3,44
3,12
116016785
199893614
-150688248,9
-155563702,9
28
29
09/04
09/05
3,08
3,86
4
4,62
3,88
4,26
240626096
257802656
22290368,02
35858928,86
30
31
09/06
09/07
4,06
4,28
4,54
4,96
4,44
4,84
243540678
262369420
177924324,4
347692772,6
32
33
09/08
09/09
4,84
5,65
6,3
6,95
5,95
6,4
236535041
173425124
470820602,2
497501390,5
34
35
09/10
09/11
4,08
3,82
4,88
4,4
4,12
4,02
206146761
228128227
311969305,6
241170890,3
36
09/12
3,94
4,5
4,5
269358200
510529090,3
0
125
GARAN-T. GARANTİ BANKASI A.Ş.
Dönem
En Düşük En Yüksek Kapanış
Sayısı Dönemler
Fiyat
Fiyat
Fiyatı
(Yıl/Ay)
(TL)
(TL)
(TL)
Toplam İşlem
Miktarı
(Adet)
ADI
0
1
07/01
4,22
5,85
5,3
455570245
2
3
07/02
07/03
5,1
4,85
6,05
6,45
5,4
6,25
321867814
377389329
29547323,52
312589320,3
4
5
07/04
07/05
6,15
6,3
7,7
7,4
6,7
7,25
278946933
291804119
231604726,8
443825904,3
6
7
07/06
07/07
6,4
7,3
7,35
9,75
7,35
9
240746148
390609146
684572052,3
836032741,5
8
9
07/08
07/09
6,95
7,9
8,95
9,4
8,35
9,25
583850045
407665074
1069572760
1395704819
10
11
07/10
07/11
9,05
9,15
10,8
11,2
10,3
10,45
404857128
396009281
1569215016
1675461409
12
07/12
9,9
11,1
10,5
220303896
1675461409
13
14
08/01
08/02
7,4
6,85
10,5
8,4
7,4
7,3
687305608
617504478
0
-946259098,8
15
16
08/03
08/04
5,85
5,9
7,25
7,45
6
6,85
809268550
616076767
-1582112959
-1442998851
17
18
08/05
08/06
5,3
2,8
6,95
5,85
5,6
2,82
519535700
1390313339
-1773612478
-3145692200
19
20
08/07
08/08
2,56
3,48
4,3
3,96
3,92
3,56
2338320242
1253375149
-1828707236
-2664290668
21
22
08/09
08/10
2,84
1,83
4,08
2,92
3,06
2,52
2645238800
4545487936
-4370896346
-3161546344
23
24
08/11
08/12
1,68
2
2,6
2,68
2,28
2,6
3495942183
1776750809
-2097563941
-738872145,8
25
09/01
2,11
2,82
2,25
2776365789
26
27
09/02
09/03
1,96
1,88
2,34
2,43
2,07
2,36
2076546719
2737378365
-2555796431
-515205286,6
28
29
09/04
09/05
2,36
3,16
3,36
4,04
3,36
3,84
2396517881
2449710025
1881312594
3217518063
30
31
09/06
09/07
3,56
3,96
4,34
5,5
4,18
5,2
1765832927
1410524129
4258906712
5119875985
32
33
09/08
09/09
5
5,1
6,05
5,9
5,55
5,6
1004252845
790163479
5167697549
5365238419
34
35
09/10
09/11
5,35
5,1
6,4
6,05
5,5
5,2
1075451739
784505060
4597058606
3977712506
36
09/12
5,2
6,4
6,35
642307462
4566494346
0
126
HALKB-TÜRKİYE HALK BANKASI A.Ş.
Dönem
En Düşük En Yüksek
Sayısı Dönemler
Fiyat
Fiyat
(Yıl/Ay)
(TL)
(TL)
Kapanış
Fiyatı
(TL)
Toplam İşlem
Miktarı
(Adet)
ADI
1
2
07/01
07/02
3
4
07/03
07/04
5
6
07/05
07/06
8
7,95
9,15
8,95
8,6
8,45
338019578
84371350
0
14696503,39
7
8
07/07
07/08
8,4
6,6
9,75
9,1
9
8,75
100427319
159894176
3537912,391
118661719,1
9
10
07/09
07/10
8,3
8,9
10,6
11,2
9,8
9,85
75756305
66992288
141717985,9
130067153,2
11
12
07/11
07/12
8,95
9,85
10,1
12,2
10
12,2
86422157
41099739
201459369,8
242559108,8
13
08/01
8,4
12,2
8,6
106243335
14
15
08/02
08/03
7,7
6,85
9,45
8,45
7,8
7,4
90243332
139070000
-174989634,4
-218449009,4
16
17
08/04
08/05
7,15
6,45
8,7
8,05
7,35
7,35
93615153
81711436
-287905413,2
-277691483,7
18
19
08/06
08/07
5,7
5
7,4
8
5,8
7,95
47018099
75007741
-319178041,7
-246670558,7
20
21
08/08
08/09
6,45
4,95
7,95
7,3
6,6
5,75
59284288
99266138
-294097989,1
-325778671,4
22
23
08/10
08/11
3,32
3,16
5,45
4,44
4,2
4,1
402397090
297126433
-395678635,4
-256400620
24
08/12
3,6
4,78
4,6
113337132
-177640918,1
25
26
09/01
09/02
3,92
3,4
4,88
4,56
4,28
3,58
231021915
186141359
0
-186128829,8
27
28
09/03
09/04
3,16
3,64
3,76
5,65
3,64
5,6
432984589
463519155
73661923,62
514120424,1
29
30
09/05
09/06
5,05
5,05
6,4
6,5
5,9
6,1
165554542
188903765
557041972,1
641722970,2
31
32
09/07
09/08
6
7,25
8,15
9,35
7,85
8,1
131356535
163030621
736421867,5
705368415,9
33
34
09/09
09/10
7,95
8,3
9,1
10,3
8,8
9,05
114528201
132496412
760142772,9
727018669,9
35
36
09/11
09/12
8,85
9
9,75
12
9,05
11,9
97590979
69919674
672801459,3
738059821,7
0
127
ISCTR-T. İŞ BANKASI A.Ş.
Dönem
En Düşük En Yüksek
Sayısı Dönemler
Fiyat
Fiyat
(Yıl/Ay)
(TL)
(TL)
Kapanış
Fiyatı
(TL)
Toplam İşlem
Miktarı
(Adet)
ADI
0
1
07/01
5,7
7,2
6,7
421549470
2
3
07/02
07/03
6,4
5,95
7,85
7
6,7
6,7
444313387
396875390
-119943081,7
50146371,17
4
5
07/04
07/05
6,25
6
7,6
6,55
6,55
6,15
402207073
447310664
-173302002,7
-376625031,8
6
7
07/06
07/07
5,6
6,1
6,3
7,9
6,15
7,1
341103837
727791690
-181708553,5
-100842810,2
8
9
07/08
07/09
5,55
6
7
7,5
6,35
7,3
695297182
488741160
-28915515,5
329494668,5
10
11
07/10
07/11
7,05
6,95
8,7
8,25
7,95
7,65
785097778
765013353
400867193,8
459714374,8
12
07/12
7,15
8,15
7,35
412162395
212416937,8
13
14
08/01
08/02
5,6
5,2
7,35
6,3
5,8
5,65
1051131753
869920539
0
-969040437,3
15
16
08/03
08/04
4,84
4,7
6,05
6,05
4,94
5,9
774078199
687032702
-1615171827
-1080813058
17
18
08/05
08/06
4,86
3,96
5,9
5,2
5,04
4
470292723
461635436
-1388312146
-1820164651
19
20
08/07
08/08
3,64
5,2
5,75
5,9
5,4
5,7
991828456
348051977
-1157378811
-1008213678
21
22
08/09
08/10
4,3
3,24
5,95
5,3
5,35
4,28
535364947
746432122
-862205055,9
-854958142,1
23
24
08/11
08/12
3
3,44
4,54
4,22
4,02
4,1
924821872
523164559
-554691300,6
-192500452
25
09/01
3,46
4,36
3,68
656266841
26
27
09/02
09/03
3,12
3,04
3,88
3,84
3,28
3,74
572344978
738925225
-666782893,1
-112588974,4
28
29
09/04
09/05
3,68
4,58
4,7
5,5
4,62
5,3
797748989
476816262
560022918,3
829527762
30
31
09/06
09/07
4,1
4,28
4,88
5,25
4,54
5,1
639465430
586684582
911510509,5
1316746252
32
33
09/08
09/09
4,95
5,3
6,4
6,1
5,95
5,8
445050704
451388149
1485558588
1598405625
34
35
09/10
09/11
5,45
5,1
6,65
6,3
5,75
5,2
475503449
438431771
1360653900
995294091,3
36
09/12
5,1
6,4
6,3
444013919
1370998177
0
128
KCHOL-KOÇ HOLDİNG A.Ş.
Dönem
En Düşük En Yüksek Kapanış
Sayısı Dönemler
Fiyat
Fiyat
Fiyatı
(Yıl/Ay)
(TL)
(TL)
(TL)
Toplam İşlem
Miktarı
(Adet)
ADI
1
2
07/01
07/02
5,25
6,05
6,45
6,5
6
6,15
121278807
111309834
0
-31519094,92
3
4
07/03
07/04
5,5
6,2
6,5
7,55
6,3
6,75
109420374
110360701
34133129,48
13695962,63
5
6
07/05
07/06
6,3
5
7,45
7,4
7,25
5,25
100928949
112243114
79519190,24
-9339941,676
7
8
07/07
07/08
5,2
4,9
6,5
5,95
6
5,95
289864476
195371261
57551860,48
252923121,5
9
10
07/09
07/10
5,75
5,75
6,7
6,85
6,35
6,35
121429668
201666488
284878297,3
303211614,4
11
12
07/11
07/12
5,75
5,85
6,5
6,4
6
6,35
116974307
100081484
264220178,7
346105029,2
13
08/01
4,52
6,4
4,56
170766675
14
15
08/02
08/03
4,2
3,66
4,98
4,56
4,64
3,72
211481923
195999375
-136386940,9
-306253065,9
16
17
08/04
08/05
3,66
3,34
4,5
4,52
4,4
3,44
174468299
109524299
-173324838,1
-264285696,6
18
19
08/06
08/07
3,24
3,04
3,66
4,72
3,34
4,66
79009238
106083650
-305671487,9
-207165241,5
20
21
08/08
08/09
4,04
3,3
4,66
4,5
4,14
3,92
69030001
94760391
-253927500,3
-250768820,6
22
23
08/10
08/11
2,04
1,98
3,82
3
2,84
2,52
226207339
190573084
-273643720
-262433538,6
24
08/12
2,29
2,68
2,62
121625584
-178231211,2
25
26
09/01
09/02
2,19
2,05
2,84
2,51
2,31
2,12
204780239
196240871
0
-265684462,4
27
28
09/03
09/04
1,98
2,31
2,36
2,94
2,34
2,92
290886665
361924945
-5417446,3
333528137,1
29
30
09/05
09/06
2,9
2,48
3,64
3,02
3,52
2,66
223245602
306603500
484369760,1
382168593,4
31
32
09/07
09/08
2,52
3,26
3,54
4,1
3,46
3,98
382842371
311566971
704957259,2
927505095,6
33
34
09/09
09/10
3,64
3,7
4,02
4,2
3,9
3,84
214923578
355879636
1006687466
850100426,6
35
36
09/11
09/12
3,68
3,7
3,94
4,46
3,74
4,42
201744359
217482530
741468848,7
936058480,8
0
129
KOZAA-KOZA DAVETİYE MAĞAZA İŞLETMELERİ VE İHRACAT A.Ş.
Dönem
En Düşük En Yüksek Kapanış
Sayısı Dönemler
Fiyat
Fiyat
Fiyatı
(Yıl/Ay)
(TL)
(TL)
(TL)
Toplam İşlem
Miktarı
(Adet)
ADI
1
2
07/01
07/02
12
11,4
14,8
14,4
14,2
11,7
22402692
9815707
0
4948972,686
3
4
07/03
07/04
9,7
9,5
12
12,8
11,8
10
12292258
8223896
15103446,69
9371640,383
5
6
07/05
07/06
9,65
13,1
15,4
18,4
14,8
17,8
15585011
17042824
21704127,35
34888198,74
7
8
07/07
07/08
17,2
17,2
20,8
22,4
20
19,4
10611210
7061641
40783315,41
39696909,1
9
10
07/09
07/10
19,5
19,9
25,3
23,3
23,1
21,4
6158989
9779782
41183561,62
40032999,03
11
12
07/11
07/12
9,8
9,15
22,8
11,8
9,8
10,5
4289342
16344549
35743657,03
36052044,75
13
08/01
6,55
12,8
8,1
43637786
14
15
08/02
08/03
6,85
5,45
8,7
7,25
7,25
5,9
24942926
20328320
-36150239,98
-46314399,98
16
17
08/04
08/05
5,55
5,15
6,75
6,45
6,25
5,3
31081678
16144664
-41134120,32
-53553092,62
18
19
08/06
08/07
3,88
4,04
5,35
5,2
4,54
5,18
20202026
17790654
-55614523,85
-38437340,67
20
21
08/08
08/09
4,46
1,22
5,45
4,6
4,6
1,45
19725926
167466968
-52584216,9
-197259822,4
22
23
08/10
08/11
0,77
0,66
1,39
1,07
0,92
0,91
156115973
145872438
-277835808,5
-245815029,4
24
08/12
0,76
0,93
0,88
99271284
-204938618,3
25
26
09/01
09/02
0,84
0,88
1,04
1,48
0,91
1,39
188836291
449172376
0
257769775,9
27
28
09/03
09/04
1,34
1,45
1,67
1,86
1,6
1,78
373969674
286959111
473085648,8
648060716,5
29
30
09/05
09/06
1,78
2,74
3,26
3,18
2,74
2,88
920991326
519488276
921868948,5
732964120,9
31
32
09/07
09/08
2,82
2,96
3,1
3,52
2,96
3,08
339992785
373071633
732964120,9
519780330,6
33
34
09/09
09/10
2,96
3,26
3,36
4,28
3,32
3,92
205300067
401772690
684020384,2
802188822,5
35
36
09/11
09/12
3,52
4,66
5,22
5,1
4,86
4,82
654722861
348613439
1179617295
1084540903
0
130
KRDMD-KARDEMİR KARABÜK DEMİR ÇELİK SANAYİ VE TİCARET A.Ş.
Dönem
En Düşük En Yüksek Kapanış
Sayısı Dönemler
Fiyat
Fiyat
Fiyatı
(Yıl/Ay)
(TL)
(TL)
(TL)
Toplam İşlem
Miktarı
(Adet)
ADI
1
2
07/01
07/02
0,47
0,62
0,67
0,81
0,65
0,71
393362832
968370926
0
263723374,8
3
4
07/03
07/04
0,61
0,78
0,86
0,99
0,84
0,84
1086850938
1188408882
1176678163
667360070,4
5
6
07/05
07/06
0,81
0,82
0,96
0,94
0,94
0,91
873639050
435645487
1308028707
1525851451
7
8
07/07
07/08
0,9
1,01
1,2
1,29
1,16
1,16
1005018041
943462481
2262864681
2330254858
9
10
07/09
07/10
1,08
1,25
1,43
1,47
1,38
1,33
633033224
377891716
2782421446
2679360069
11
12
07/11
07/12
1,27
1,31
1,41
1,43
1,34
1,38
275460919
174373452
2679360069
2708422311
13
08/01
0,96
1,39
0,98
261132815
14
15
08/02
08/03
0,99
0,99
1,31
1,2
1,18
1,03
330430270
286537356
-174885715
-352265983
16
17
08/04
08/05
1
1,13
1,25
1,35
1,25
1,19
334712093
252714881
-17553889,7
-132424290
18
19
08/06
08/07
1,06
1,02
1,23
1,28
1,15
1,21
211394660
230583192
-119989310
-13566298,5
20
21
08/08
08/09
1,08
0,65
1,3
1,13
1,12
0,8
236965219
496665689
-164362347
-350611980
22
23
08/10
08/11
0,43
0,39
0,77
0,55
0,53
0,46
428199426
368421108
-526929391
-572982030
24
08/12
0,42
0,51
0,5
218354743
-403150563
25
26
09/01
09/02
0,48
0,49
0,64
0,55
0,5
0,5
735723573
309551474
0
-758160329
27
28
09/03
09/04
0,44
0,51
0,53
0,73
0,51
0,7
405426297
682879151
-532923497
-36284114,9
29
30
09/05
09/06
0,7
0,49
0,85
0,56
0,81
0,53
941016730
665944949
402857025,8
497992018,5
31
32
09/07
09/08
0,49
0,53
0,58
0,67
0,54
0,62
550935838
1314769009
559207111,6
934855399,9
33
34
09/09
09/10
0,57
0,59
0,65
0,65
0,63
0,6
774578618
732680464
1322144709
833691066,2
35
36
09/11
09/12
0,52
0,52
0,6
0,66
0,53
0,64
499337696
1010617518
459187794,2
1181057450
0
131
PETKM-PETKİM PETROKİMYA HOLDİNG A.Ş.
Dönem
En Düşük En Yüksek Kapanış
Sayısı Dönemler
Fiyat
Fiyat
Fiyatı
(Yıl/Ay)
(TL)
(TL)
(TL)
Toplam İşlem
Miktarı
(Adet)
ADI
1
2
07/01
07/02
4,8
5,25
5,65
7,15
5,2
6,3
53892586
147913189
0
12399657,25
3
4
07/03
07/04
5,65
6,9
7,35
8,25
7,1
7,65
120764097
71628399
97644902,19
105603613,2
5
6
07/05
07/06
7,2
8,4
9,5
9,25
9
8,95
80917864
55697595
151339797,2
167721442,8
7
8
07/07
07/08
8,75
8,35
11,3
10,1
10,4
9,85
180931790
66321941
220936675,1
268309490,1
9
10
07/09
07/10
9,5
9,1
10,6
10,6
9,9
9,65
47716075
78283650
255296015,1
234420375,1
11
12
07/11
07/12
8,8
8,55
9,95
10,1
9,35
8,6
49492871
30560398
232268511,2
203679751,8
13
08/01
6,1
8,75
6,5
26572519
14
15
08/02
08/03
6,15
6,3
7,6
8,35
7,3
6,5
44305153
47264803
7421359,77
-30621042,6
16
17
08/04
08/05
6,4
6,7
7,35
7,55
7
7,25
33421796
22365964
-21825833,2
-15247608,5
18
19
08/06
08/07
4,95
4,52
7,3
5,6
5
5,35
10499234
39017096
-25300066,6
-4346440,92
20
21
08/08
08/09
5,25
4,04
5,85
5,55
5,45
4,4
45987689
40515144
-19675670,6
-40872335,3
22
23
08/10
08/11
3,3
3,68
4,48
5,06
4,18
4,84
19411879
47314483
-31330903,3
897802,5332
24
08/12
4,42
4,88
4,62
21161821
-1862434,99
25
26
09/01
09/02
3,38
3,62
4,78
4,1
3,8
4
23671237
15027691
0
-702341,717
27
28
09/03
09/04
3,64
4,02
4,2
4,96
4,08
4,62
8376543
45685080
4084254,283
16720553,01
29
30
09/05
09/06
4,65
5,6
5,95
6,6
5,6
6,5
60826349
48153344
44794252,55
83316927,75
31
32
09/07
09/08
6,35
6,85
7,25
7,55
6,95
7,15
43945086
28924287
97965289,75
93833248,75
33
34
09/09
09/10
6,45
7,15
7,95
8,05
7,5
7,3
41531382
46062172
110445801,5
79737686,88
35
36
09/11
09/12
6,3
6,3
7,5
7,35
6,5
7,3
32995069
62773433
57740974,21
114535985
0
132
SAHOL-H.Ö SABANCI HOLDİNG A.Ş
Dönem
En Düşük En Yüksek Kapanış
Sayısı Dönemler
Fiyat
Fiyat
Fiyatı
(Yıl/Ay)
(TL)
(TL)
(TL)
Toplam İşlem
Miktarı
(Adet)
ADI
1
2
07/01
07/02
5,15
5,45
6,1
6,3
5,85
5,7
91674167
112136112
0
-2749087,755
3
4
07/03
07/04
5,2
5,6
5,85
6,8
5,7
6,05
89018134
131580969
45183753,63
12288511,38
5
6
07/05
07/06
5,65
5,85
6,5
6,6
6,15
6,55
104894654
56990824
30799332,67
80191380,14
7
8
07/07
07/08
6,45
5,9
8,15
7,25
7,3
7,2
86221107
61362091
80191380,14
137008131,1
9
10
07/09
07/10
6,85
7
7,9
8,1
7,75
7,95
40709222
42710987
166086146,8
197148682,8
11
12
07/11
07/12
6,05
6,2
8
7
6,6
6,45
66861022
54338071
168004134,7
147627358,1
13
08/01
4,8
6,45
4,9
73516589
14
15
08/02
08/03
4,95
4,1
6,05
5,45
5,55
4,16
61907833
86666247
-58977502,48
-137940083,1
16
17
08/04
08/05
4,08
4,28
4,86
4,94
4,76
4,64
128333525
52643032
-42512590,14
-37726859,95
18
19
08/06
08/07
4,04
3,56
4,64
6
4,18
5,8
35791069
66820607
-56815430,09
-949020,9565
20
21
08/08
08/09
4,9
3,82
6,3
5,08
5
4,82
40056954
65159556
-35283552,96
2984757,71
22
23
08/10
08/11
2,64
2,48
4,52
3,98
3,7
3,1
87532751
71937802
14159151,45
1689932,442
24
08/12
2,62
3,62
3,5
79681409
62247803,28
25
26
09/01
09/02
2,62
2,41
3,66
3,36
3,16
2,46
124370336
156644292
0
-135371944,7
27
28
09/03
09/04
2,29
2,86
3,08
4,22
2,86
4,1
182385375
154198774
-54568297,54
72418928,1
29
30
09/05
09/06
4,1
3,86
4,74
4,54
4,68
4,14
85289341
75624576
141716517,7
128371004,3
31
32
09/07
09/08
4,04
5
5,55
6,05
5,5
5,8
81535396
107658954
204506705,2
260899490,6
33
34
09/09
09/10
5,4
5,2
5,9
5,95
5,75
5,55
100913851
137656468
301265031
292087933,1
35
36
09/11
09/12
5,05
5,2
5,75
5,75
5,35
5,75
69459349
68456929
282165169
350622098
0
133
SISE-ŞİŞE CAM
Dönem
En Düşük En Yüksek Kapanış
Sayısı Dönemler
Fiyat
Fiyat
Fiyatı
(Yıl/Ay)
(TL)
(TL)
(TL)
Toplam İşlem
Miktarı
(Adet)
ADI
1
2
07/01
07/02
4,54
5,4
5,6
6,25
5,55
5,7
31693299
22349794
0
22129896,31
3
4
07/03
07/04
4,84
4,95
5,9
5,75
5,3
5,25
37237012
47316646
17211800,38
5382638,884
5
6
07/05
07/06
4,86
4,9
5,35
5,55
5,35
5,4
25246848
24232034
30629486,88
43677505,19
7
8
07/07
07/08
5,35
4,72
6,5
6,05
5,85
5,45
29088549
36889407
39883346,63
43489078,14
9
10
07/09
07/10
5,35
2,29
6,1
6,15
6
2,56
26383425
45054360
62836923,14
24085504,69
11
12
07/11
07/12
2,19
2,23
2,6
2,44
2,3
2,36
47561734
32592611
2044701,131
9804846,607
13
08/01
1,63
2,36
1,66
78815787
14
15
08/02
08/03
1,55
1,53
2
1,94
1,9
1,65
108502476
51864511
-12058623,78
-33563421,02
16
17
08/04
08/05
1,62
1,68
1,99
2,01
1,98
1,7
64083257
47322466
27055876,14
-14530533,37
18
19
08/06
08/07
1,3
1,19
1,78
1,66
1,3
1,61
56482529
89327289
-71013062,37
-691579,5434
20
21
08/08
08/09
1,54
1,23
1,75
1,68
1,61
1,57
54880072
50010933
-18984936,88
6576206,657
22
23
08/10
08/11
0,89
0,85
1,51
1,27
1,24
1,08
95189346
81841297
18858702,91
26653112,15
24
08/12
0,97
1,14
1,09
45024366
45192556,98
25
26
09/01
09/02
0,92
0,91
1,18
1,04
0,97
0,95
65249500
48268953
0
-58718520,38
27
28
09/03
09/04
0,88
1
1,03
1,25
1
1,25
52690913
109693239
-27103972,58
82589266,42
29
30
09/05
09/06
1,2
1,16
1,35
1,3
1,31
1,26
138835717
121291162
147379267,7
199361194,3
31
32
09/07
09/08
1,16
1,34
1,38
1,69
1,34
1,59
187470851
275302136
318660826,7
436647456,4
33
34
09/09
09/10
1,44
1,53
1,65
1,88
1,58
1,59
177147162
283037292
495696510,4
309700575,7
35
36
09/11
09/12
1,48
1,5
1,69
1,91
1,52
1,87
170468695
354679828
204172335,9
489646343,8
0
134
SKBNK-ŞEKERBANK
Dönem
En Düşük En Yüksek Kapanış
Sayısı Dönemler
Fiyat
Fiyat
Fiyatı
(Yıl/Ay)
(TL)
(TL)
(TL)
Toplam İşlem
Miktarı
(Adet)
ADI
1
2
07/01
07/02
4,4
5,1
5,15
7,55
5,1
6,5
34609933
52261539
0
37461209,41
3
4
07/03
07/04
5,7
5,9
6,8
8,15
6,15
7,15
30389410
25295451
31935862,14
34746467,8
5
6
07/05
07/06
6,95
8,35
9,5
9,75
9,5
9,4
11890003
5038527
46636470,8
49155734,3
7
8
07/07
07/08
9
3,86
13,1
12,3
11,6
5,06
6089577
6231283
50789523,25
46330169,07
9
10
07/09
07/10
4,04
4,5
5,28
5,45
4,86
4,94
55663641
29489449
64286182,3
62113275,53
11
12
07/11
07/12
4,22
4,44
5,38
5,45
4,5
5,2
33957962
31937097
44548812,42
60675465,36
13
08/01
3,56
5,15
3,6
30234149
14
15
08/02
08/03
3,3
2,5
4,12
3,9
3,98
2,54
35912195
59300996
-5063439,688
-60975807,34
16
17
08/04
08/05
2,48
2,13
3,22
3,2
3,18
2,27
49923367
72830176
-16449561,1
-70221373,29
18
19
08/06
08/07
2,05
1,99
2,43
2,64
2,38
2,5
53526826
94043253
-30780554,13
22751759,12
20
21
08/08
08/09
2,25
1,66
2,9
2,54
2,27
1,9
75695744
157866270
-48285785,25
-120043180,7
22
23
08/10
08/11
0,91
0,85
1,86
1,36
1,23
1,05
110599704
93278097
-156133610,4
-176252415,7
24
08/12
0,93
1,14
1,09
63873825
-142794697,8
25
26
09/01
09/02
0,93
0,86
1,21
1,03
1
0,88
108177970
62258356
0
-101698316,1
27
28
09/03
09/04
0,81
0,93
0,95
1,62
0,94
1,54
70903613
281790258
-40923790,63
175523798,8
29
30
09/05
09/06
1,43
1,5
1,96
1,69
1,75
1,61
322014756
211970098
242357050,1
275826012,9
31
32
09/07
09/08
1,58
1,88
1,93
2,66
1,87
2,44
310711058
260741486
480007565,3
593664110,5
33
34
09/09
09/10
2,19
2,44
2,62
3
2,5
2,52
173122561
152258489
670160125,8
561404062,3
35
36
09/11
09/12
2,24
2,24
2,62
2,64
2,28
2,58
113555032
152356833
471755352,8
578405135,9
0
135
TAVHL-TAV HAVALİMANLARI HOLDİNG A.Ş.
Dönem
En Düşük En Yüksek
Sayısı Dönemler
Fiyat
Fiyat
(Yıl/Ay)
(TL)
(TL)
Kapanış
Fiyatı
(TL)
Toplam İşlem
Miktarı
(Adet)
ADI
0
1
2
07/01
07/02
10,1
11,1
10,3
39993651
3
4
07/03
07/04
9,55
10,8
11,8
12,2
11,5
11,6
27572597
17177467
-3776286,133
-1322362,276
5
6
07/05
07/06
11,3
11,3
13
12,6
12,4
11,5
10578620
4582278
1788996,547
-1383349,76
7
8
07/07
07/08
11,5
10,1
13,7
12,5
12,6
11,4
13201884
5956460
-1383349,76
-886978,0937
9
10
07/09
07/10
10,3
10
11,6
11,6
11,1
10,7
6856222
9807874
695226,9832
-530757,2668
11
12
07/11
07/12
10,4
10,3
11,9
11,1
11,1
10,7
8930464
3231214
-1126121,533
-1126121,533
13
08/01
8
10,8
8,1
4842248
14
15
08/02
08/03
7,6
6,6
8,35
7,55
7,65
7,3
8450006
15853342
-11819711,68
-4310233,887
16
17
08/04
08/05
6,95
8,45
8,95
10,6
8,95
10,6
11267802
7444024
6957568,113
14401592,11
18
19
08/06
08/07
7,1
7,25
10,5
8,15
8,15
7,75
4457263
6985463
12697344,5
13473507,05
20
21
08/08
08/09
7,25
5,55
8,5
7,8
7,3
6,4
6460124
5019797
7530192,971
6303131,482
22
23
08/10
08/11
2,46
2,62
6,2
4,54
3,7
3,08
40088928
81388084
-7202764,047
-49592391,13
24
08/12
2,74
4,04
3,34
84078605
-56059976,13
25
26
09/01
09/02
2,47
2,64
2,92
3,38
2,84
2,76
43228951
34007234
0
4880796,5
27
28
09/03
09/04
2,68
2,88
3,02
3,42
2,9
3,38
19993464
65640309
10761227,09
66677045,87
29
30
09/05
09/06
3,3
3,78
4,08
4,24
3,76
4,08
99970052
111057677
84620388,53
118420551,1
31
32
09/07
09/08
3,94
4,08
4,2
4,64
4,1
4,18
40650337
114779811
127801398,1
54014376,74
33
34
09/09
09/10
3,82
3,9
4,24
4,66
4,08
4,14
58490244
196376857
67940625,31
-4408743,056
35
36
09/11
09/12
3,86
3,9
4,32
4,82
3,94
4,74
134036645
178995213
-91823946,32
56041664,42
0
136
TCELL-TURKCELL İLETİŞİM İŞLETMELERİ A.Ş.
Dönem
En Düşük En Yüksek
Sayısı Dönemler
Fiyat
Fiyat
(Yıl/Ay)
(TL)
(TL)
Kapanış
Fiyatı
(TL)
Toplam İşlem
Miktarı
(Adet)
ADI
1
2
07/01
07/02
6,45
6,85
8,1
8,05
7,85
7,15
91009693
91147559
0
17857218,65
3
4
07/03
07/04
6,65
6,85
7,45
7,85
7,1
7,6
60327112
72731854
25398107,65
61764034,65
5
6
07/05
07/06
7,45
7,95
8,95
8,95
8,85
8,85
57357814
37476892
111474140,1
141455653,7
7
8
07/07
07/08
8,45
8,2
9,9
9,75
9,15
9,45
85031493
89695000
138523533,3
193497888,1
9
10
07/09
07/10
8,85
9,8
10,8
11,7
10,2
11,2
49336248
63692809
212473368,1
242643646,1
11
12
07/11
07/12
10,7
12,6
13,7
13,9
12,8
12,8
90681647
55401161
278916304,9
240561654,9
13
08/01
10
13,1
10,2
91549039
14
15
08/02
08/03
9,9
10,2
13
12,4
12,1
11,1
107346955
87929721
-34719794,8
-50707016,8
16
17
08/04
08/05
9,7
8,75
12,2
10,6
10,2
9,6
111436924
259891204
-117569171
-138641431
18
19
08/06
08/07
6,95
6,5
9,8
9,35
7
8,9
92923518
147105000
-228304475
-127653685
20
21
08/08
08/09
7,6
6,6
9
8,35
7,95
8,3
90972678
126476012
-173140024
-53891212,9
22
23
08/10
08/11
6,8
7,1
8,75
9,1
7,6
8,85
112443332
81678014
-74073349,4
-12814838,9
24
08/12
7,75
9,35
8,75
71372779
5028355,883
25
26
09/01
09/02
7,75
8,25
9,45
9,55
8,85
8,45
79684229
84071026
0
-34766480,1
27
28
09/03
09/04
7,65
7,6
8,55
8,5
8,15
8,2
118637920
173459797
-21584488,9
36235443,39
29
30
09/05
09/06
7,25
7,85
8,15
8,8
8,15
8,55
262847837
164063972
299083280,4
376797793,4
31
32
09/07
09/08
8,15
9
9,5
10,4
9,35
9,75
141889129
86372775
487156004,9
493325488,8
33
34
09/09
09/10
9,3
9,8
11
10,9
10,6
10
55501960
69493056
522708879,4
478486025,6
35
36
09/11
09/12
9,15
9,3
10,3
10,8
9,3
10,6
47561596
60908026
443331802,5
487997688,2
0
137
TEBNK-TÜRK EKONOMİ BANKASI A.Ş.
Dönem
En Düşük En Yüksek Kapanış
Sayısı Dönemler
Fiyat
Fiyat
Fiyatı
(Yıl/Ay)
(TL)
(TL)
(TL)
Toplam İşlem
Miktarı
(Adet)
ADI
0
1
07/01
15,8
18,8
17
2675126
2
3
07/02
07/03
17,1
18,2
21,5
22,6
20,1
22,5
2338292
1402265
315262,8
1653788,482
4
5
07/04
07/05
21,6
21,8
28,75
26,25
24
24,2
1192982
2760046
1261689,503
1478771,772
6
7
07/06
07/07
17,7
18,9
24,4
23,2
20
19,6
1123404
2296898
1126660,071
-422410,6732
8
9
07/08
07/09
15,7
2,94
20,1
21,8
19,2
3,1
1649802
16150447
552472,3268
-15323948
10
11
07/10
07/11
2,7
2,6
3,28
3,16
3,06
2,9
58445815
22800795
-1216337,484
412290,7306
12
07/12
2,78
3,12
2,94
22163816
-891463,1517
13
14
08/01
08/02
2,06
1,92
2,96
2,35
2,22
1,97
29054182
26895223
0
-39364326,15
15
16
08/03
08/04
1,32
1,35
1,96
1,74
1,38
1,65
54098216
56878301
-83319126,65
-52692349,19
17
18
08/05
08/06
1,23
0,99
1,68
1,36
1,29
1,05
67857307
58075660
-102454374,3
-141694685,1
19
20
08/07
08/08
0,99
1,39
1,51
1,6
1,42
1,5
168470822
86164881
-31540686,14
-27437596,57
21
22
08/09
08/10
1,08
0,69
1,56
1,26
1,28
0,91
73084961
118763213
-39618423,4
-66704770,22
23
24
08/11
08/12
0,61
0,71
0,95
0,87
0,8
0,82
173716870
77648287
-46267491,4
-17149383,78
25
09/01
0,67
0,88
0,73
118785142
26
27
09/02
09/03
0,54
0,52
0,74
0,67
0,57
0,65
135170237
163052886
-145527083,9
-25954967,5
28
29
09/04
09/05
0,64
0,93
0,95
1,19
0,93
1,15
496385965
454980483
406381195,6
721367683,8
30
31
09/06
09/07
1
1,12
1,29
1,57
1,2
1,51
263913520
275815731
821472812,1
1023737681
32
33
09/08
09/09
1,47
1,62
2,01
1,89
1,83
1,83
307033973
198839938
1126082339
1236548971
34
35
09/10
09/11
1,75
1,99
2,35
2,26
2,23
2,03
324379139
165675810
1431176455
1314589774
36
09/12
2
2,96
2,8
217125727
1459340258
0
138
THYAO-TÜRK HAVAYOLLARI A.O.
Dönem
En Düşük En Yüksek Kapanış
Sayısı Dönemler
Fiyat
Fiyat
Fiyatı
(Yıl/Ay)
(TL)
(TL)
(TL)
Toplam İşlem
Miktarı
(Adet)
ADI
1
2
07/01
07/02
6,05
7,35
7,65
8,7
7,3
7,5
42263473
28001863
0
1993976,785
3
4
07/03
07/04
6,75
6,95
7,65
9,25
7
8,4
26999576
41873826
-10005834,77
917772,0118
5
6
07/05
07/06
8,1
7,9
9,05
9,75
8,4
9,65
25877797
18002864
-8616153,199
7440455,234
7
8
07/07
07/08
9,15
7,65
10,9
9,65
9,7
9,05
30617790
40424616
-3931866,766
12237979,63
9
10
07/09
07/10
8,45
8
9,6
9,8
9,4
8,3
32598805
36654604
33498069,85
9061667,184
11
12
07/11
07/12
7,7
7,95
8,75
9,2
7,9
8,6
47798599
33489411
-20527941,72
-19188365,28
13
08/01
6,75
8,55
7,05
17355379
14
15
08/02
08/03
7
5,85
7,95
7,2
7,3
6,25
19465729
29545550
-18741837,04
-30778912,96
16
17
08/04
08/05
6,15
6,15
7,4
7,45
7,15
6,6
43707286
23027259
-4554541,361
-11639851,82
18
19
08/06
08/07
4,95
4,2
6,9
6,3
5
5,95
24433542
46679287
-34820391,67
-3700867,002
20
21
08/08
08/09
5,75
5,45
7,05
7,3
6,5
6,6
21661235
38727652
-368369,3097
9051870,366
22
23
08/10
08/11
3,7
4,42
6,75
5,8
4,76
5,3
49944363
71554312
-6177066,549
13526294,73
24
08/12
4,74
5,7
5,7
59274705
72800999,73
25
26
09/01
09/02
5,65
5,5
6,65
6,75
6,1
5,6
47348672
45025994
0
-42556702,16
27
28
09/03
09/04
5,15
6,5
6,55
8,2
6,55
7,85
42787270
74344507
230567,84
43962630,78
29
30
09/05
09/06
7,4
1,78
9,1
2,33
8,85
2,32
86342050
261118019
104909960,2
356532778,5
31
32
09/07
09/08
2,08
2,3
2,46
2,96
2,32
2,88
575740020
493581748
508043310,1
881968876,7
33
34
09/09
09/10
2,74
3,7
4,06
4,76
3,86
4,22
276287542
232407339
1074532921
1070147877
35
36
09/11
09/12
3,98
4,7
5
5,9
4,86
5,7
325337506
201981193
1306177048
1440831177
0
139
TKFEN-TEKFEN HOLDİNG A.Ş.
Dönem
En Düşük En Yüksek
Sayısı Dönemler
Fiyat
Fiyat
(Yıl/Ay)
(TL)
(TL)
Kapanış
Fiyatı
(TL)
Toplam İşlem
Miktarı
(Adet)
ADI
1
07/01
2
3
07/02
07/03
4
5
07/04
07/05
6
7
07/06
07/07
8
9
07/08
07/09
10
11
07/10
07/11
5,7
6,3
6
91777943
12
07/12
5,75
6,6
6,45
20663479
13370486,41
13
14
08/01
08/02
5,8
5,75
7,6
6,85
6,4
6,45
34505158
20587277
0
-5887007,424
15
16
08/03
08/04
6,15
6,5
7,8
8,5
6,6
7,9
16604945
12682811
-13434709,7
-8361585,297
17
18
08/05
08/06
7,4
8,5
9,15
9,95
9,15
9,4
27325143
16511856
18963557,7
22949178,12
19
20
08/07
08/08
7,05
7,25
9,55
8,5
8,05
8,2
32573449
26377076
16434488,32
30150567,84
21
22
08/09
08/10
5,85
3,5
8,9
6,9
7,15
4,16
39719998
77483688
24290240,26
-23111545,34
23
24
08/11
08/12
2,96
2,8
5,08
3,48
3,46
2,92
102518655
197482367
-77272344,2
-205055052,3
25
09/01
2,6
3,38
2,7
264321205
26
27
09/02
09/03
2,56
2,43
2,86
2,98
2,62
2,88
128841064
148431796
-273851175,5
-179394578
28
29
09/04
09/05
2,74
3,44
3,54
3,92
3,46
3,8
191660562
192215749
-26066128,4
70041746,1
30
31
09/06
09/07
3,1
3,32
3,68
4,08
3,54
3,98
166880655
110210065
156359326,3
237566742,6
32
33
09/08
09/09
3,88
3,74
4,48
4,48
4,12
4,28
176478399
109500143
202271062,8
252581939,3
34
35
09/10
09/11
4,1
4,06
5
4,9
4,34
4,06
99326944
78726975
206229365,4
127502390,4
36
09/12
4,06
4,98
4,09
107930790
26610565
0
0
140
TOASO-TOFAŞ TÜRK OTOMOBİL FABRİKASI A.Ş.
Dönem
En Düşük En Yüksek Kapanış
Sayısı Dönemler
Fiyat
Fiyat
Fiyatı
(Yıl/Ay)
(TL)
(TL)
(TL)
Toplam İşlem
Miktarı
(Adet)
ADI
1
2
07/01
07/02
4,68
5,05
6,15
5,9
5,35
5,25
12619180
13009481
0
-8003354,199
3
4
07/03
07/04
5
5,15
5,6
6,45
5,3
6,05
14417454
26268674
-8003354,199
2099981,955
5
6
07/05
07/06
5,55
5,85
6,65
6,5
6,3
6,35
12435432
14284395
6621957,228
14313554,54
7
8
07/07
07/08
6
4,65
6,9
6,25
6,25
5,95
13041088
13561877
8517515,424
16993688,55
9
10
07/09
07/10
5,7
5,85
6,35
6,45
6,05
6,15
15483110
23143002
18184697,01
18184697,01
11
12
07/11
07/12
5,1
5,8
6,25
6,5
5,75
6,15
15237147
12004864
20172150,97
20172150,97
13
08/01
4,95
6,45
5,3
13374369
14
15
08/02
08/03
5,2
4,06
6
5,65
5,7
4,3
12992301
16111210
-3884921,55
-15132370,04
16
17
08/04
08/05
4,22
4,58
4,9
5,1
4,86
4,74
23953480
23125085
6003053,489
-2891209,973
18
19
08/06
08/07
3,46
3,18
4,72
4,3
3,56
4,2
18125215
22366261
-18139406,72
232879,1027
20
21
08/08
08/09
3,74
2,54
4,52
4,16
4
2,68
21503041
29193101
-6934801,231
-31082181,07
22
23
08/10
08/11
1,28
0,94
2,55
1,94
1,79
1,13
69857878
96092299
-44833731,86
-104410957,2
24
08/12
0,99
1,25
1,15
92373653
-83093960,39
25
26
09/01
09/02
1,13
1,13
1,37
1,28
1,2
1,23
156062524
76722573
0
-39451860,67
27
28
09/03
09/04
1,18
1,39
1,55
2,15
1,46
1,94
103195452
147370727
13540398,47
79469407,92
29
30
09/05
09/06
1,96
2,56
2,78
3,06
2,52
2,7
160002238
102248081
138006812,1
93017656,42
31
32
09/07
09/08
2,56
2,82
3,18
3,94
3,08
3,76
79724586
106729781
147024634
219448414
33
34
09/09
09/10
3,56
3,5
4,54
4,38
4,18
3,8
54621508
112231113
233939834,5
198229934,9
35
36
09/11
09/12
3,48
3,98
4,16
4,76
4,08
4,72
51320231
70899755
237474817,4
301102802,7
0
141
TTKOM-TÜRK TELEKOMÜNİKASYON A.Ş.
Dönem
En Düşük En Yüksek
Sayısı Dönemler
Fiyat
Fiyat
(Yıl/Ay)
(TL)
(TL)
Kapanış
Fiyatı
(TL)
Toplam İşlem
Miktarı
(Adet)
ADI
0
1
2
07/01
07/02
3
4
07/03
07/04
5
6
07/05
07/06
7
8
07/07
07/08
9
10
07/09
07/10
11
12
07/11
07/12
13
08/01
14
15
08/02
08/03
16
17
08/04
08/05
4,3
4,68
4,6
419934278
18
19
08/06
08/07
4,06
3,4
4,6
4,5
4,12
4,28
168972872
200088384
111696500,3
231749530,7
20
21
08/08
08/09
4,16
3,62
4,54
4,28
4,24
3,82
87339911
91416332
181184319
145171824,6
22
23
08/10
08/11
2,94
2,94
3,78
3,58
3,3
3,4
144484210
74690316
124531223,2
157208236,4
24
08/12
3,16
3,64
3,48
47633328
173086012,4
25
26
09/01
09/02
3,48
3,7
4,48
4,28
4,26
3,9
97658947
77193339
0
30732456,84
27
28
09/03
09/04
3,74
3,82
4,12
4,52
3,86
4,4
78957812
127426251
1642736,627
85379987,28
29
30
09/05
09/06
3,92
4,26
4,38
5,06
4,28
4,82
92808455
85607436
137836940,1
172079914,5
31
32
09/07
09/08
4,36
4,44
4,88
4,82
4,48
4,58
83594664
297890514
127067403,1
48675162,6
33
34
09/09
09/10
4,26
4,4
4,62
5,02
4,46
4,58
153448309
150070527
65724974,71
2792173,065
35
36
09/11
09/12
4,36
4,34
4,74
4,6
4,4
4,56
54238044
103623134
-40027335,4
31711757,41
142
TUPRS-TÜPRAŞ TÜRKİYE PETROL RAFİNELERİ A.Ş.
Dönem
En Düşük En Yüksek Kapanış
Sayısı Dönemler
Fiyat
Fiyat
Fiyatı
(Yıl/Ay)
(TL)
(TL)
(TL)
Toplam İşlem
Miktarı
(Adet)
ADI
0
1
07/01
23,3
26
25
23888202
2
3
07/02
07/03
25,1
25
29,25
32,5
27,25
31
24556016
19776947
7080804,399
18946972,6
4
5
07/04
07/05
26,75
27,25
31,5
36,25
28
31,25
18643390
26735113
10115893,13
7145325,014
6
7
07/06
07/07
28,25
30,75
31,5
34,5
31,5
32
15461956
32718830
22607281,01
11701004,35
8
9
07/08
07/09
26,25
28,25
32,25
34
29,75
32
26992284
18124560
16199718,35
21715888,78
10
11
07/10
07/11
29,25
30
33,25
33,5
33
30,75
30879441
23908200
48735399,66
35073571,09
12
07/12
30,5
34,5
34,25
10919874
44628460,84
13
14
08/01
08/02
26,25
26,75
35,75
33,25
29,5
31,25
20184321
12184850
0
-1687515,34
15
16
08/03
08/04
27,25
28,5
34
35,25
29,5
34,5
19473456
14586741
-8178667,34
3166575,664
17
18
08/05
08/06
28,25
26,25
34
31,5
30,5
28,25
15317888
13173440
-163399,988
-3299933,32
19
20
08/07
08/08
25
27,5
32,25
32,5
31,75
28
21303427
12427615
15065089,95
5122997,954
21
22
08/09
08/10
21,1
17,1
27,75
23
23,6
19,5
20380832
31872047
66099,78891
-5876146,26
23
24
08/11
08/12
10,4
12,9
19,5
18,2
15
16,2
46723410
24513261
-5362702,2
649984,4644
25
09/01
14,2
17,3
15,7
29454300
26
27
09/02
09/03
13,7
14,3
15,9
17
15,5
16,7
23646199
39357800
14097442,47
44709064,69
28
29
09/04
09/05
13,4
15,6
16,3
19,2
16
19,2
51454839
47809024
85518074,94
133327098,9
30
31
09/06
09/07
18,4
17,2
20,9
19,2
18,8
19
32106085
42303576
111494961,1
145337821,9
32
33
09/08
09/09
18,8
21,1
24,1
25,75
22,5
24,6
56687241
35284242
167798804,2
185630625,4
34
35
09/10
09/11
24,2
23,7
29,25
27,75
26
26
30733325
15832182
176806205,4
178956254,8
36
09/12
25,75
30,5
29,75
19084767
192014253,3
0
143
VAKBN-TÜRKİYE VAKIFLAR BANKASI T.A.O.
Dönem
Sayısı
Dönemler
(Yıl/Ay)
En Düşük En Yüksek Kapanış
Fiyat
Fiyat
Fiyatı
(TL)
(TL)
(TL)
Toplam İşlem
Miktarı
(Adet)
ADI
1
2
07/01
07/02
3,6
3,3
7,85
4,04
3,64
3,46
103707224
258684112
0
-248575800,2
3
4
07/03
07/04
3,2
3,44
3,54
4,16
3,48
3,86
208173849
190059495
-113875074,4
-82198491,91
5
6
07/05
07/06
3,56
3,12
4,08
3,6
3,6
3,38
158162813
148981435
-216028564,4
-203613444,9
7
8
07/07
07/08
3,36
3,14
4,46
4,1
4,18
3,72
287670364
261241794
-62393447,99
-7968074,244
9
10
07/09
07/10
3,58
3,9
4,16
4,64
4,12
4,42
197527852
256448624
162314556,8
266280215,2
11
12
07/11
07/12
3,58
3,78
4,5
4,24
3,84
4,14
314995642
142729208
129325588,2
209998618,8
13
08/01
2,82
4,14
2,88
410535569
14
15
08/02
08/03
2,64
2,39
3,16
3
2,88
2,43
379907161
417670477
-402437781,4
-765331802,4
16
17
08/04
08/05
2,37
2
2,84
2,62
2,6
2,1
513126493
570026703
-776249387,4
-1162396509
18
19
08/06
08/07
1,57
1,41
2,14
2,49
1,59
2,37
495582265
970902179
-1623201071
-868054931,7
20
21
08/08
08/09
2,2
1,71
2,62
2,48
2,26
2,13
551038924
802148362
-1261654163
-1188731585
22
23
08/10
08/11
1,09
1,01
2,15
1,59
1,49
1,2
1115051496
1286456553
-1462234782
-1905840490
24
08/12
1,07
1,25
1,17
918133735
-1803825630
25
26
09/01
09/02
1,11
1,07
1,37
1,25
1,2
1,08
1111525310
559657323
0
-839480963,7
27
28
09/03
09/04
1,04
1,25
1,3
1,85
1,26
1,81
556704654
758059425
-454070049,4
202914785,6
29
30
09/05
09/06
1,83
1,85
2,33
2,43
2,13
2,33
846833569
726754129
372281499,4
848430756,3
31
32
09/07
09/08
2,27
2,84
3,18
3,6
3,1
3,32
438355318
376271924
1209712612
1308731539
33
34
09/09
09/10
3,06
3,32
3,5
4,12
3,4
3,68
247944138
231035086
1443973796
1420870288
35
36
09/11
09/12
3,08
3,14
3,7
4,28
3,12
4,26
329192989
234186077
1134153813
1360122835
0
144
VESTL-VESTEL ELEKTRONİK SANAYİ VE TİCARET A.Ş.
Dönem
En Düşük En Yüksek Kapanış
Sayısı Dönemler
Fiyat
Fiyat
Fiyatı
(Yıl/Ay)
(TL)
(TL)
(TL)
Toplam İşlem
Miktarı
(Adet)
ADI
0
1
07/01
3,32
3,74
3,5
26343365
2
3
07/02
07/03
3,4
3,16
3,92
3,58
3,5
3,54
117528594
52772890
-76088626,47
-33367715,52
4
5
07/04
07/05
3,38
3,38
3,94
3,68
3,48
3,52
60411306
22561145
-72203555,09
-73707631,42
6
7
07/06
07/07
3,04
3,12
3,52
3,48
3,14
3,26
21711122
68206681
-86372452,59
-101529492,8
8
9
07/08
07/09
2,68
2,92
3,26
3,44
2,94
3,34
26117452
61165509
-104231298,2
-66590984,96
10
11
07/10
07/11
3,18
3,1
4,04
3,54
3,44
3,16
162701025
62918656
-130914646
-176673668,6
12
07/12
2,88
3,2
2,9
26475454
-199839690,8
13
14
08/01
08/02
1,88
1,82
2,9
2,22
1,9
2,04
32826583
56562824
0
-25882983,62
15
16
08/03
08/04
1,52
1,64
2,06
2,36
1,66
2,26
28776718
89737843
-39738440,43
25072223,95
17
18
08/05
08/06
2,09
1,83
2,31
2,23
2,14
1,97
88197569
37918653
-23035540,95
-34411136,85
19
20
08/07
08/08
1,41
1,77
1,95
2,11
1,76
1,94
64299762
34370423
-15359355,52
-15359355,52
21
22
08/09
08/10
1,32
0,75
1,92
1,38
1,44
0,89
11751246
20260900
-22410103,12
-33666158,68
23
24
08/11
08/12
0,67
0,75
1
0,93
0,84
0,85
16092882
22997033
-33178495,59
-30623269,7
25
09/01
0,77
0,9
0,81
22259619
26
27
09/02
09/03
0,76
0,74
0,88
0,83
0,8
0,81
19442109
32606697
-15042094,92
3072736,744
28
29
09/04
09/05
0,8
1,29
1,54
1,59
1,42
1,48
236675513
155241103
162988623,9
204386251,4
30
31
09/06
09/07
1,51
1,44
1,66
1,75
1,51
1,67
79279301
61915734
125106950,4
155066176,5
32
33
09/08
09/09
1,62
2,1
2,59
2,48
2,31
2,35
301412958
183772393
282467529,9
340500917,1
34
35
09/10
09/11
2,25
2,07
2,66
2,62
2,36
2,17
202961058
165432575
246445792,7
141170517,7
36
09/12
2,15
2,6
2,6
206526755
347697272,7
0
145
YKBNK-YAPI VE KREDİ BANKASI A.Ş.
Dönem
En Düşük En Yüksek Kapanış
Sayısı Dönemler
Fiyat
Fiyat
Fiyatı
(Yıl/Ay)
(TL)
(TL)
(TL)
Toplam İşlem
Miktarı
(Adet)
ADI
1
2
07/01
07/02
2,26
2,78
2,9
3,4
2,74
3,06
478817918
788609950
0
163091867,1
3
4
07/03
07/04
2,64
2,84
3,08
3,38
2,96
3
635786311
622993550
452085644,8
198273457,8
5
6
07/05
07/06
2,86
2,74
3,04
3,1
2,98
2,92
400769700
481000410
331863357,8
331863357,8
7
8
07/07
07/08
2,9
3,28
4,22
3,82
3,88
3,74
1211127671
842717875
919076774
1512100464
9
10
07/09
07/10
3,56
3,8
3,96
4,58
3,86
4,54
584227358
844085139
1804214143
2561726447
11
12
07/11
07/12
4,1
3,94
4,6
4,5
4,4
4,12
452681689
271723505
2652262785
2555218676
13
08/01
3,06
4,12
3,1
521789282
14
15
08/02
08/03
2,44
2,5
3,28
3,04
2,76
2,58
885997306
519164715
-693360698
-1058698831
16
17
08/04
08/05
2,52
2,62
2,94
3,08
2,84
2,92
549789811
436310962
-770713692
-637923399
18
19
08/06
08/07
2,23
2,05
2,96
2,84
2,24
2,66
270457961
429257367
-900971553
-667325138
20
21
08/08
08/09
2,54
2,19
2,86
2,76
2,66
2,7
286772356
429186896
-739018227
-400186467
22
23
08/10
08/11
1,35
1,47
2,64
2,14
1,92
1,91
489431117
359656623
-457097062
-344368867
24
08/12
1,68
2,2
2,1
222380622
-207519253
25
26
09/01
09/02
1,67
1,53
2,18
1,95
1,79
1,65
395335027
406848858
0
-383658811
27
28
09/03
09/04
1,46
1,7
1,76
2,17
1,71
2,16
684139454
1112460817
72434158,75
1137556218
29
30
09/05
09/06
2,17
2,11
2,56
2,42
2,36
2,28
909340580
724252053
1114239792
1184328701
31
32
09/07
09/08
2,26
2,88
3,14
3,36
3,08
3,16
740381044
498891018
1823748693
1906897196
33
34
09/09
09/10
3
3,06
3,36
3,54
3,24
3,12
346506213
408579976
2022399267
1715964285
35
36
09/11
09/12
2,84
2,88
3,22
3,32
2,92
3,28
324831460
372506644
1527903966
1832682130
0
146
EK-6 LINDO 6.1 Paket Programı ile Çözülen Modelin Sonuç Çıktısı
LP OPTIMUM FOUND AT STEP
119
OBJECTIVE FUNCTION VALUE
1)
0.5733861
VARIABLE
Y1
Y2
Y3
Y4
Y5
Y6
Y7
Y8
Y9
Y10
Y11
Y12
Y13
Y14
Y15
Y16
Y17
Y18
Y19
Y20
Y21
Y22
Y23
Y24
Y25
Y26
Y27
Y28
Y29
Y30
Y31
Y32
Y33
Y34
Y35
Y36
VALUE
0.573386
0.112475
0.063714
0.036722
0.049131
0.000000
0.070436
0.003804
0.033253
0.026529
0.084224
0.055600
0.027424
0.208286
0.015021
0.132721
0.071468
0.041402
0.138092
0.059894
0.019950
0.155736
0.286146
0.000000
0.003549
0.008151
0.042050
0.058889
0.173545
0.148627
0.125640
0.015894
0.054939
0.126801
0.029805
0.066552
0.106243
REDUCED COST
0.000000
0.000000
0.000000
0.000000
0.000000
0.000000
0.000000
0.000000
0.000000
0.000000
0.000000
0.000000
0.000000
0.000000
0.000000
0.000000
0.000000
0.000000
0.000000
0.000000
0.000000
0.000000
0.000000
0.000000
0.000000
0.000000
0.000000
0.000000
0.000000
0.000000
0.000000
0.000000
0.000000
0.000000
0.000000
0.000000
0.000000
147
X1
X2
X3
X4
X5
X7
X8
X9
X10
X12
X13
X14
X15
X17
X18
X19
X21
X22
X23
X25
X27
X28
X29
X30
X6
X16
X20
X11
X24
X26
0.000000
0.000000
0.000000
0.361273
0.000000
0.000000
0.000000
0.043269
0.077741
0.000000
0.000000
0.111880
0.000000
0.000000
0.000000
0.000000
0.052857
0.000000
0.352979
0.000000
0.000000
0.000000
0.000000
0.000000
0.000000
0.000000
0.000000
0.000000
0.000000
0.000000
0.234140
0.334759
0.196461
0.000000
0.429347
0.033253
0.062584
0.000000
0.000000
0.303429
0.216365
0.000000
0.021697
0.383218
0.443872
0.018935
0.000000
0.118930
0.000000
0.427892
0.053081
0.264585
0.398817
0.042499
0.854815
0.001553
0.440173
0.057071
0.059329
0.137195
148
ÖZGEÇMĠġ
KĠġĠSEL BĠLGĠLER
Adı Soyadı
Uyruğu
Doğum Yeri ve Tarihi
Telefon
Faks
e-mail
:
:
:
:
:
:
Mehmet CEBECĠ
T.C
Eynesil / 03.01.1985
05352494382
mhmtcebeci@yahoo.com
EĞĠTĠM
Adı, Ġlçe, Ġl
: Derince Lisesi (Y.D.A), Derince, Kocaeli
Selçuk Üniversitesi Endüstri Mühendisliği Bölümü,
Üniversite
:
Selçuklu, Konya
Selçuk Üniversitesi Fen Bilimleri Enstitüsü Endüstri
Yüksek Lisans :
Mühendisliği Anabilim Dalı, Selçuklu, Konya
Derece
Lise
Bitirme Yılı
2002
2008
Ġġ DENEYĠMLERĠ
Yıl
2010
2009
Kurum
Hidroliksan Hidrolik Pres Ġmalat San.
Tic. Ltd. ġti.
AlkıĢ Damlama Sulama Sistemleri Mak.
Tic. Ltd. ġti.
YABANCI DĠLLER
Ġngilizce
Görevi
Proses Kontrol
Sorumlusu
Ġmalat Sorumlusu,
Üretim Planlama