FONKSİYONLAR
. ÜNİTE
3. ÜNİTE
1.
Kazanım
3. ÜNİTE
3. ÜNİTE
: Gerçek sayılar üzerinde tanımlanmış fonksiyon kavramını açıklar.
Tanım kümesi, değer kümesi, görüntü kümesi kavramlarını açıklar.
2.
Kazanım
: Fonksiyonların grafik gösterimini yapar.
Grafiği verilen bir fonksiyonun tanım kümesindeki bazı elemanların görüntüsü ve
görüntü kümesindeki bazı elemanların ters görüntüleri belirlenir.
Düşey (dikey) doğru testi açıklanır.
Bir f fonksiyonunun grafiğinin y = f (x) denkleminin grafiği olduğu ve grafiğin
(varsa) x eksenini kestiği noktaların f (x) = 0 denkleminin gerçek sayılardaki çözüm kümesi olduğu vurgulanır.
Tanım kümesinin bir alt kümesinin fonksiyon altındaki görüntüsünün bulunması ile
ilgili grafik yorumlama uygulamaları yapılır.
f (x) = a x + b biçimindeki grafiklerle ilgili uygulamalar yaptırılır.
Birim fonksiyon, sabit fonksiyon, doğrusal fonksiyon kavramlarını açıklar.
İki fonksiyonun eşitliğini açıklar.
3.
Kazanım
: f (x) = x n (n ∈ Z ) biçimindeki fonksiyonların grafiklerini çizer. ( Bu fonksiyonların
sadece n = 1, 2, 3, –1 için değer tablosu yardımıyla grafikleri çizdirilir.)
4.
Kazanım
: Bire bir ve örten fonksiyonları açıklar.
Bir fonksiyonun bire bir ve örtenliği grafik üzerinde yatay doğru testi ile incelenir.
Parçalı tanımlı şekilde verilen fonksiyonların grafikleri çizdirilir.
Mutlak değer fonksiyonu bir parçalı tanımlı fonksiyon olarak açıklanır.
Değer kümesinin bir alt kümesinin fonksiyon altındaki ters görüntüsünün bulunmasıyla ilgili grafik yorumlama uygulamaları yapılır.
3. ÜNİT
FONKSİYONLAR
Fonksiyon: A ve B boş olmayan iki küme olmak üzere A nın her elemanını B nin bir ve yalnız bir elemanına
eşleyen f bağıntısına A dan B ye bir fonksiyon denir.
f
f : A ⎯⎯→ B veya A ⎯⎯→ B biçiminde gösterilir.
f
A
x
A kümesi fonksiyonun tanım kümesidir.
x
B kümesi fonksiyonun değer kümesidir.
x
f (A) = {f (x) : x ∈ A } kümesi ise f fonksiyonunun
B
f(A) görüntü
kümesi
görüntü kümesidir.
x
f (A) ⊂ B dir.
Tan›m Kümesi
De¤er Kümesi
f : A → B bağıntısının fonksiyon olabilmesi için:
I.
Tanım kümesinde açıkta eleman kalmamalı.
II. Tanım kümesindeki her elemanın yalnız bir görüntüsü olmalıdır.
ÖRNEK 1
A = {Gizem, Canberk, Aybars, Ecem}
B = {Pazartesi, Salı, Çarşamba, Perşembe, Cuma, Cumartesi, Pazar }
olmak üzere, A kümesindeki elemanlar aynı sınıfta bulunan
4 arkadaşın isimlerini ve B kümesindeki elemanlar da haftanın
günlerini göstermektedir.
β
A
A → B ye tanımlanan β bağıntısı;
x
Gizem ve Canberk pazartesi günü doğmuştur.
x
Aybars salı günü doğmuştur.
x
Ecem çarşamba günü doğmuştur.
Pazartesi
Sal›
Çarflamba
Perflembe
Cuma
Cumartesi
Pazar
Gizem
Canberk
Aybars
Ecem
biçiminde ise grafiği yandaki gibidir.
B
Bu bağıntıda A kümesinde açıkta eleman kalmamıştır ve A kümesindeki her elemanın yalnız bir görüntüsü vardır.
Bu koşullar sağlandığı için β bağıntısı A → B ye bir fonksiyondur.
β1
A
Gizem
Canberk
Aybars
Ecem
β2
P.tesi
Sal›
Çarfl.
Perfl.
Cuma
C.tesi
Pazar
B
A
Gizem
Canberk
Aybars
Ecem
β3
P.tesi
Sal›
Çarfl.
Perfl.
Cuma
C.tesi
Pazar
B
A
Gizem
Canberk
Aybars
Ecem
P.tesi
Sal›
Çarfl.
Perfl.
Cuma
C.tesi
Pazar
B
Ecem’in doğduğu bir gün bulunmak zo-
Gizem hem P.tesi hem Salı günü doğmuş
Gizem ve Canberk aynı gün (Salı) doğ-
rundadır.
olamaz.
muş olabilirler.
b1 bağıntısı A → B ye fonksiyon değildir.
b2 bağıntısı A → B ye fonksiyon değildir.
b 3 bağıntısı A → B ye bir fonksiyondur.
256
Fonksiyon
Düşey ( Dikey) Doğru Testi
ÖRNEK 2
A = {1, 2, 3}
ve
Grafiği verilmiş bir bağıntının fonksiyon olup olmadı-
B = {a, b, c, d }
ğını anlamak için, y eksenine paralel doğrular çizilir.
olmak üzere, A → B ye tanımlanan aşağıdaki bağın-
Bu doğrular fonksiyonun belirttiği eğriyi en az bir ve
tıların fonksiyon olup olmadığını tespit edip fonksiyon
en çok bir noktada kesiyorsa verilen bağıntı fonksi-
olanların görüntü kümelerini bulunuz.
a.
yondur.
f = {(1, a), (2, b), (3, b) }
b. g = {(1, a), (2, c) }
c.
ÖRNEK 3
h = {(1, a), (1, b), (2, c), (3, d) }
Aşağıda grafikleri verilmiş olan bağıntıların fonksiyon
Çözüm
olup olmadığını tespit ediniz.
a.
b.
y
y
β2
β1
x
1
3
ESEN YAYINLARI
Çözüm
257
x
Fonksiyon
ÖRNEK 4
Aşağıda grafiği verilen bazı bağıntıların fonksiyon olup olmadığı tespit edilmiştir. İnceleyiniz.
y
y
C
y = g(x)
y = h(x)
x
0
x
0
y eksenine paralel olan C doğrusu grafiği
y eksenine paralel çizilen doğruların hiçbiri grafiği
2 noktada kestiğinden y = g (x ) fonksiyon
birden fazla noktada kesmediğinden y = h(x) bir
değildir.
fonksiyondur.
y
y
y = p(x)
y = k(x)
x
0
0
x
y eksenine paralel çizilen doğruların hiçbiri
Grafiği kesen ve y eksenine paralel olan bir doğru
grafiği birden fazla noktada kesmediğinden
çizersek grafikle çakışık olur. Yani grafiği
y = k ( x ) bir fonksiyondur.
∞ noktada keser. O halde, y = p(x) bir fonksiyon
değildir.
FONKSİYON MAKİNESİ
2
f(x) = x2 + 1
5
Şekil 1
Girdi
Çıktı
1
2
2
5
3
10
4
17
Şekil 2
Şekil 1 deki fonksiyon makinesine giren her sayı karesinin bir fazlası olarak çıkmaktadır.
Giren sayıları genellikle x , çıkan sayıları y, fonksiyonu da f ile göstereceğiz.
Bu fonksiyon makinesi için Şekil 2 deki tabloda bazı girdi ve çıktı değerleri verilmiştir. İnceleyiniz.
258
Fonksiyon
ÖRNEK 5
ÖRNEK 8
f : A → B, f (x) = x 2 olmak üzere,
Girdi
f(x) = ?
Çıktı
Girdi
Çıktı
1
4
2
7
3
10
4
13
A = { –2, –1, 0, 1, 2 } ve B = { –1, 0, 1, 2, 3, 4 }
ise f (A) görüntü kümesini bulunuz.
Çözüm
Yukarıdaki fonksiyon makinesi ve bu makineye giren
bazı sayılarla bu sayıların çıktıları tabloda gösterilmiştir. Buna göre, f (x) in kuralını bulunuz.
Çözüm
ÖRNEK 6
bağıntısı bir fonksiyon ise tanım ve görüntü kümelerini bulunuz.
Çözüm
ESEN YAYINLARI
f = {(a, 2), ( b, 1), (c, 3), (d, 5)}
ÖRNEK 9
f : A → B, f (x) = 2 – x
fonksiyonunun görüntü kümesi f (A) = { –1, 0, 2 } ise
tanım kümesini bulunuz.
Çözüm
ÖRNEK 7
f : A → B, f (x) = 2 x + 1
olmak üzere, A = { –2, 0 1} ve B = { –3, 1, 3, 5, 6 }
ise f (A) görüntü kümesini bulunuz.
Çözüm
ÖRNEK 10
f : [ –2, 3] → R , f (x) = 2 x + 3
olduğuna göre f ( [ –2, 3]) görüntü kümesini bulunuz.
Çözüm
259
Fonksiyon
ÖRNEK 11
ÖRNEK 14
f (x) = 2 x + 5 olduğuna göre
x =
f (a + 1) – f (1 – 2a) = 30
2 f ( x) – 1
1 + f ( x)
olduğuna göre, f (x + 1) ifadesinin eşitini bulunuz.
eşitliğini sağlayan a kaçtır?
Çözüm
Çözüm
ÖRNEK 12
ÖRNEK 15
f (x) = 3 x – 5
f (2 x – 1) = 6 x + 4
olduğuna göre aşağıdakilerin herbirini bulunuz.
a. f (1 – x)
b. f e
x +1
o
3
olduğuna göre, aşağıdakilerin herbirini bulunuz.
c. f2 (3)
a. f (3)
ESEN YAYINLARI
Çözüm
b. f (–1)
c. f (9)
Çözüm
ÖRNEK 13
f (2 x – 1) =
mx – 2
3
olmak üzere, f (3) = 6 eşitliğini sağlayan m kaçtır?
Çözüm
ÖRNEK 16
f (x) = 3 x – 7 olmak üzere, f (2 x + 1) fonksiyonunun
f (x) cinsinden değerini bulunuz.
Çözüm
260
Fonksiyon
ÖRNEK 17
ÖRNEK 20
f (x) – f (x + 1) = 1 – x
f (x) = 2 x+1 olmak üzere f (3 x – 1) fonksiyonunun
f (x) cinsinden değerini bulunuz.
olduğuna göre f (10) – f (1) ifadesinin eşiti kaçtır?
Çözüm
Çözüm
ÖRNEK 21
ÖRNEK 18
f : [ –1, 3] → R , f (x) = x 2 – 2
f (x) = x + f (x + 1) ve f (1) = 8
olduğuna göre,
olduğuna göre f (4) kaçtır?
lunuz.
ESEN YAYINLARI
Çözüm
f ` [ –1, 3 ] j görüntü kümesini bu-
Çözüm
ÖRNEK 22
ÖRNEK 19
f (x) = x .f (x – 1) ve f (1) = 2
olduğuna göre f (4) kaçtır?
Çözüm
f : [ –1, 2) → R , f (x) = x 2 – 2 x
olduğuna göre, f ` [ –1, 2 ) j görüntü kümesini bulunuz.
Çözüm
261
ALIŞTIRMALAR -
1.
A = {1, 2, 3 } ve B = {3, 4, 5, 6 }
3.
olmak üzere A → B ye tanımlanan aşağıdaki
f (x) = 2 x + 1 ve g (x) =
x+1
2
fonksiyonlarına göre aşağıdakileri bulunuz.
bağıntılardan hangileri fonksiyondur?
a.
1
f1 = {(1, 3), (2, 3), (3, 4) }
a . f (2)
1
b. fc m
2
c . f (0)
d . g (2a – 1)
e . g (0)
f. f e 1 –
b. f2 = {(1, 6), (2, 5), (3, 3) }
c.
f3 = {(1, 3), (2, 4), (3, 5), (1, 6) }
d. f4 = {(2, 3), (3, 4), (2, 5) }
e.
x
o
2
Aşağıda grafiği verilen bağıntıların fonksiyon
olup olmadığını tespit ediniz.
y
y = f(x)
4.
1
x
0
–3
y
2
–2
ESEN YAYINLARI
2.
f5 = {(1, 4), (2, 3)}
f : A → B , f (x) =
x+1
2
fonksiyonu için A = {–2, –1, 0, 1, 2 } ve
B = {–1, –
1
1
3
, 0, , 1,
, 2 } olduğuna göre
2
2
2
f (A) görüntü kümesini bulunuz.
y = g(x)
0
x
2
–2
5.
y
–3 –1 0
fonksiyonu için f (A) = {1, 3, 5 } olduğuna göre
y = h(x)
1
3
5
f : A → R , f (x) = 2 x – 3
A kümesini bulunuz.
x
y
y = k(x)
6.
0
262
x
2 x – 3y + x y + 1 = 0
eşitliğini sağlayan
kuralını bulunuz.
y = f (x) fonksiyonunun
Fonksiyon
7.
f : A → B, f (x) =
x –1
2
11. Aşağıdaki fonksiyonların görüntü kümelerini
ve f (A) = ( –1, 2)
bulunuz.
olduğuna göre, A kümesini bulunuz.
a. f : [–1, 3 ] → R , f (x) = 2 x – 1
b. f : [–2, 2) → R , f (x) = 4 – x
c. f : [–3, 2 ] → R , f (x) = x 2 – 1
8.
Aşağıdaki fonksiyonların görüntü kümelerini
bulunuz.
a. f : R → R , f (x) = 4 – x
12.
f (n – 1) = 2 + n.f (n) ve f (2) = 4
olduğuna göre f (4) ifadesinin eşiti kaçtır?
c. f : R → R , f (x) = x 2
ESEN YAYINLARI
b. f : R → R , f (x) = –2
13.
f (x) =
9
x
.f (x + 1) ve f (5) =
16
3
olduğuna göre f (2) ifadesinin değeri kaçtır?
9.
f : A → B , f (x) = x 2 + 1
fonksiyonu için A = [ –2, 1) olduğuna göre f (A)
görüntü kümesini bulunuz.
14. f (x) = 2 x – 3 olmak üzere,
f (3 x – 1)
fonksiyonunun f (x) cinsinden değerini bulunuz.
10.
f : A → B, f(x) = x2 + 4x
15.
f (x + 1) = 32 x – 1
fonksiyonu için A = [ –3, 2 ] ise f(A) görüntü
olduğuna göre
kümesini bulunuz.
değerini bulunuz.
f (x – 1)
in
f (x)
türünden
263
Fonksiyon
BİR FONKSİYONUN GRAFİĞİ
ÖRNEK 25
f : A → B , f (x) = y fonksiyonu verildiğinde
y
y = f(3x + 1)
f = {(x, y) : y = f (x) , x ∈ A , y ∈ B}
3
kümesine düzlemde karşılık gelen noktaların oluştur2
duğu şekle f fonksiyonunun grafiği denir.
–2
0
ÖRNEK 23
y
Yukarıda y = f (3 x + 1) fonksiyonunun grafiği çizil-
f(x)
miştir. Buna göre
4
0
f (4) + f (– 5)
f (1)
kaçtır?
Çözüm
2
–4
x
1
2
x
4
Şekildeki grafik f (x) fonksiyonuna aittir. Buna göre;
f (– 4) , f (0) , f (2) , f (4) değerlerini bulunuz.
ESEN YAYINLARI
Çözüm
ÖRNEK 26
Aşağıda grafiği verilen fonksiyonların tanım ve görüntü kümeleri bulunmuştur. İnceleyiniz.
ÖRNEK 24
a.
y
y
2
1
–3
4
0
–2
y = f(x)
Yukarıda y = f (x) fonksiyonunun grafiği verilmiştir.
Buna göre f (x) in tanım ve görüntü kümelerini bulunuz.
x
0
x
Tanım kümesi: R , Görüntü kümesi: [ 0, ∞ )
b.
y
Çözüm
1
–2
0
2
x
–1
Tanım kümesi: [ –2, 2 ] , Görüntü kümesi: [ –1, 1]
264
Fonksiyon
ÖRNEK 27
ÖRNEK 29
f (x) = x 2 + m x + n
Aşağıda grafiği verilen fonksiyonların tanım ve görüntü kümeleri bulunmuştur. İnceleyiniz.
fonksiyonunun x eksenini kestiği noktalar A (–1, 0)
a.
ve B (2, 0) olduğuna göre m ve n değerlerini
y
bulunuz.
1
–2
–1
0
1
Çözüm
x
2
–1
–2
Tanım kümesi : [ –2, 2)
Görüntü kümesi : [ –2, 1)
b.
y
2
–1
0
1
2
x
Tanım kümesi : [ –2, 2)
Görüntü kümesi : [ 0, 2)
ESEN YAYINLARI
–2
ÖRNEK 30
y
y = f(x)
2
y = f ( x ) fonksiyonunun grafiğinin ( varsa ) x eksenini kestiği noktalar f(x ) = 0 denkleminin çözüm
1
–3
kümesinde bulunan elemanlardır.
0
2
x
y = f (x) in grafiği verilmiştir. Buna göre f (x) = 1
denkleminin kaç gerçel kökü vardır?
ÖRNEK 28
Çözüm
f (x) = 2 x – 4
fonksiyonunun x eksenini kestiği noktanın apsisi
kaçtır?
Çözüm
265
Fonksiyon
DOĞRUSAL FONKSİYON
ÖRNEK 31
Kuralı bir doğru denklemi olan ( f (x) = a x + b ) fonk-
y
siyonlara doğrusal fonksiyon denir.
–1
3
ÖRNEK 33
x
0
f (x) doğrusal fonksiyon olmak üzere, f (0) = 3 ve
y = f(x)
f (1) = 7 ise f (3) kaçtır?
Şekildeki grafik y = f (x) fonksiyonuna aittir.
Çözüm
Buna göre f (x) > 0 eşitsizliğini sağlayan x tam sayılarının toplamı kaçtır?
Çözüm
f (x) = a x + b Doğrusal Fonksiyonunun Grafiği
y = a x + b doğrusunun grafiğini çizmek için doğrunun geçtiği herhangi iki nokta bulunur. Eksenleri
ESEN YAYINLARI
kestiği noktaları bulmak tercih edilir.
ÖRNEK 32
ÖRNEK 34
f : R → R , f (x) = 2 x + 2
fonksiyonunun grafiğini çiziniz.
Çözüm
y
y = f(x)
1
–5
–3
4
0
x
Şekildeki grafik y = f (x) fonksiyonuna aittir.
Buna göre f (x) ≤ 0 eşitsizliğini sağlayan kaç tane x
tam sayısı vardır?
Çözüm
ÖRNEK 35
f : R → R , f (x) = 2 x
fonksiyonunun grafiğini çiziniz.
Çözüm
266
Fonksiyon
ÖRNEK 37
y
Aşağıda grafikleri verilen doğruların eğimlerini bulunuz.
b
0
a.
x
a
b.
y
y
x y
+ =1
a b
B(0, 1)
B(0, 1)
x eksenini ( a, 0 ) , y eksenini ( 0, b ) noktala-
α
rında kesen doğrunun denklemi
x y
+ = 1 dir.
a b
α
A(–2, 0)
x
A(3, 0)
O
O
Çözüm
ÖRNEK 36
y
–2
0
x
y = f (x) fonksiyonunun grafiği çizilmiştir. Buna göre
ESEN YAYINLARI
y = f(x)
1
Konum
x2
x
f (x) , f (3) ve f (x + 1)
ifadelerinin eşitini bulunuz.
α
x1
t
Çözüm
t1
t2
zaman
Şekildeki konum–zaman grafiğinde bir aracın
t1 anındaki konumu x1
t 2 anındaki konumu x 2 dir.
Δx = x 2 – x1 ve Δt = t 2 – t1 olmak üzere
l doğrusunun eğimi olan
ml = tanα =
Tx
Tt
değeri t1 ile t 2 süreleri arasındaki ortalama hızı
gösterir.
267
x
Fonksiyon
Fonksiyon
ÖRNEK 38
ÖRNEK 40
Aşağıdaki fonksiyonların grafiklerini çizerek tanım ve
f : (–1, 3 ] → R , f (x) = 3 – 2 x
görüntü kümelerini belirleyiniz.
a. y = 3
fonksiyonunun grafiğini çizip görüntü kümesini bulunuz.
b. y = x – 1
Çözüm
Çözüm
ESEN YAYINLARI
BİRİM FONKSİYON
f : A → A fonksiyonunda f (x) = x ise f fonksiyonuna birim fonksiyon denir. Başka bir ifadeyle tanım
kümesindeki her elemanın görüntüsü kendisine eşittir.
Birim fonksiyon Ι(x) = x biçiminde de gösterilir.
A
ÖRNEK 39
f : [–2, 1 ] → R , f (x) = 2 x – 1
A
a
a
b
b
c
c
fonksiyonunun grafiğini çizip görüntü kümesini bulunuz.
Şema ile ifade edilmiş olan
Çözüm
Ι : A → A fonksiyonu birim fonksiyondur.
ÖRNEK 41
f : R → R , f (x) = (a + 2)x + b – 1
fonksiyonu birim fonksiyon ise a + b kaçtır?
Çözüm
268
Fonksiyon
SABİT FONKSİYON
KOLAYLIK
f : A → B ve c ∈ B olsun. ∀x ∈ A için
Tanımlı olduğu bölgede
f (x) = c ise f fonksiyonuna sabit fonksiyon denir.
ax + b
cx + d
f (x) =
∀x ∈ A için f (x) = 0 ise f fonksiyonuna sıfır fonksiyonu denir.
sabit fonksiyon ise
Sıfır fonksiyonu da özel bir sabit fonksiyondur.
a b
dir.
=
c d
g
f
A
B
C
D
1
2
–1
0
2
4
0
1
3
6
1
2
f (x) = 4 fonksiyonu
g (x) = 0 fonksiyonu
sabit fonksiyondur.
sıfır fonksiyonudur.
ÖRNEK 44
Tanımlı olduğu bölgede
f (x) =
4x + m
2x + 1
sabit fonksiyon ise m kaçtır?
Çözüm
ÖRNEK 42
EŞİT FONKSİYONLAR
fonksiyonu sabit fonksiyon ise f (10) kaçtır?
Çözüm
ESEN YAYINLARI
f : R → R, f (x) = (a – 5)x + a – 1
f : A → B ve g : A → B iki fonksiyon olsun.
∀ x ∈ A için f (x) = g (x) ise f ile g fonksiyonlarına
eşit fonksiyonlar denir ve f = g şeklinde gösterilir.
ÖRNEK 45
A = {1, 6 } ve B = { 2, 5, 7 } olmak üzere
f : A → B , f (x) = x + 1
g : A → B , g (x) = x 2 – 6 x + 7
ÖRNEK 43
Tanımlı olduğu bölgede, f (x) =
x+a
sabit fonksi2x – 3
fonksiyonları eşit fonksiyonlar mıdır?
Çözüm
yon ise a reel sayısı kaçtır?
Çözüm
269
ALIŞTIRMALAR -
1.
4.
y
4
2
Aşağıdaki tablonun sol sütununda bulunan
fonksiyonların grafiklerini sağ sütundan bulup
eşleştiriniz.
3
2
–2
0
1
a
1
4
1
2
5
y
x
1
–3
0
f(x) = – x + 1
1
x
f : A → B fonksiyonunun grafiğine göre aşağıdab
ki boşlukları doldurunuz.
2
y
a. f (x) fonksiyonunun tanım kümesi .......... dir.
1
f(x) = 2x – 4
1
b. f (x) fonksiyonunun görüntü kümesi ........ dir.
0
x
c. f (0) + f (4) = ................. dir.
e. f (a) = 4 ise a = .............. dir.
f. f (2) = .............. dir.
c
ESEN YAYINLARI
d. f (a) = –3 ise a = .............. dir.
3
f(x) = x
0
f(x) =
f (x) =
2−x
2
4
x–4
3
1
0
si kaçtır?
5.
f (x) = x 2 – a x + b – 1
fonksiyonu x eksenini A (1, 0) ve B (–3, 0)
noktalarında kestiğine göre a + b kaçtır?
270
x
y
fonksiyonunun x eksenini kestiği noktanın apsi-
3.
2
–4
d
2.
y
f(x) doğrusal fonksiyonu için
f(0) = 3 ve f(1) + f(2) = 12
olduğuna göre, f(3) kaçtır?
2
x
Fonksiyon
6.
9.
Aşağıdaki fonksiyonların tanım(T) ve görüntü(G)
kümelerini bulunuz.
f (x) = (2 – a) x + 1 – a2
fonksiyonu birim fonksiyon olduğuna göre,
a.
y
f (a) kaçtır?
2
1
–4
x
2
0
10.
y = f(x)
f (x) =
2x – 4
ax + 1
fonksiyonu sabit fonksiyon olduğuna göre,
b.
f (a) kaçtır?
y
3
—
2
y = g(x)
0
x
2
1
11.
ESEN YAYINLARI
–2
7.
f (x) =
3x + 1
2ax – 3
fonksiyonu tanımlı olduğu değerler için sabit
fonksiyon ise f (a) kaçtır?
y
5
12. Aşağıdaki ifadelerden doğru olanlar için boş
3
kutuya “ D ” yanlış olanlar için “ Y ” yazınız.
–1
0
x
2
y = f(3 – 2x)
f (x) = (2a – 1) x + 3 fonksiyonunun sabit
1
fonksiyon olması için a =
olmalıdır.
2
Şekildeki grafik y = f (3 – 2x) fonksiyonuna
aittir. Buna göre f (–1) + f (3) + f (5) ifadesinin
Tanımlı olduğu değerler için f (x) =
eşiti kaçtır?
sabit fonksiyondur.
2x – 1
4x – 2
f (x) = (a – 1)x fonksiyonunun birim fonksiyon olması için a = 1 olmalıdır.
8.
2
f (x) = a x + ( b + 1)x + c + 2
fonksiyonu birim fonksiyon olduğuna göre,
Her fonksiyon bir bağıntıdır ama her
a + b + c kaçtır?
bağıntı bir fonksiyon değildir.
271
Fonksiyon
f (x) = x n (n ∈ Z ) BİÇİMİNDEKİ FONKSİYONLARIN
f (x) = x 3 Fonksiyonunun Grafiği
GRAFİKLERİ
f (x) = x 3 fonksiyonunun grafik çizimini de aşağıdaki
Bu bölümde f (x) = x n fonksiyonlarının n = 1, 2, 3,
değer tablosu yardımıyla yapacağız.
–1 değerleri için grafiklerini çizeceğiz.
n = 1 için f (x) = x doğrusu elde edileceğinden ve
doğru grafiklerini de daha önce çizdiğimizden n = 2
n = 3 ve n = –1 için oluşacak;
x
–2
–1
0
1
2
f(x) = x3
–8
–1
0
1
8
Tablodaki bilgileri koordinat düzlemine taşırsak aşa-
f (x) = x 2 , f (x) = x 3 ve f (x) =
1
x
ğıdaki grafiği elde ederiz.
y
fonksiyonlarının grafik çizimlerini değer tabloları yar8
dımıyla yapacağız.
y = x3
f (x) = x 2 Fonksiyonunun Grafiği
f (x) = a x 2 fonksiyonlarının grafik çizimlerini ilerideki
sınıflarda ayrıntılı olarak öğreneceksiniz. Bu fonksiyonların özel bir durumu olan f (x) = x
2
1
fonksiyonu-
–4 –3 –2 –1
x
–3
–2
–1
0
1
2
3
f(x) = x2
9
4
1
0
1
4
9
ESEN YAYINLARI
nun grafik çizimini ise aşağıdaki tablodan yararlanarak yapacağız.
x
0 1 2 3 4
–1
–8
Tablodaki bilgileri koordinat düzlemine taşırsak aşa-
Siz de değer tablosu yardımıyla aşağıda grafikleri
ğıdaki grafiği elde ederiz.
kabaca çizilmiş olan f(x) = – x 2 ve f(x) = – x 3
fonksiyonlarının grafiklerini çiziniz.
y
y
f(x) = x2
9
0
x
4
y = –x2
y
1
–5 –4 –3 –2 –1 0
y = –x3
1
2
3
4
5
x
0
272
x
Fonksiyon
f (x) = x
–1
=
BİRE BİR FONKSİYON
1
Fonksiyonunun Grafiği
x
Boş olmayan A ve B kümeleri için f : A → B fonk-
1
fonksiyonunun grafik çizimini de aşağıdaki
f (x) =
x
siyonunun tanım kümesindeki her farklı elemanın
görüntüsü farklı ise, f fonksiyonuna bire bir fonksiyon
değer tablosu yardımıyla yapacağız.
f(x) = 1
x
1
2
1
3
–1
–2
–3
–1
0
1
tanımsız
x
1
denir.
1
3
1
2
∀a, b ∈ A için,
3
2
koşulu sağlanıyorsa f fonksiyonu bire birdir.
a ≠ b ⇒ f (a) ≠ f ( b) ya da f (a) = f ( b) ⇒ a = b
f(x) = 1
a
x
3
b
c
2
1
3
0
1 1
3 2
x
1
–1
–2
–3
Siz de değer tablosu yardımıyla aşağıda grafiği
1
kabaca çizilmiş olan f(x ) = –
fonksiyonunun
x
grafiğini çiziniz.
y
f(x) =
f
A
1
2
3
a
4
c
b
B
1
2
3
4
f bire bir değildir.
ÖRNEK 46
ESEN YAYINLARI
1
2
B
f bire birdir.
1
–1
f
A
y
f : R → R , f (x) = 2 x + 1
fonksiyonunun bire bir olup olmadığını araştırınız.
Çözüm
ÖRNEK 47
f : R → R , f (x) = x 3 – x fonksiyonu bire bir midir?
Çözüm
1
x
0
x
ÖRNEK 48
f : R → R , f (x) = x 5 fonksiyonu bire bir midir?
Çözüm
273
Fonksiyon
Yatay Doğru Testi
ÖRNEK 52
f : R → R , f (x) = x 2
x eksenine ( tanım kümesine ) paralel çizilecek
fonksiyonunun grafiğini çizip bire bir olup olmadığını
doğruların tamamı grafiği birden fazla noktada
tespit ediniz.
kesmiyorsa fonksiyon bire birdir.
Çözüm
ÖRNEK 49
y
y = g(x)
x
0
ÖRNEK 53
x eksenine paralel çizdiğimiz doğrular, grafiği
en çok bir noktada kestiğinden y = g (x) bire birdir.
f : R+ → R , f (x) = x 2
fonksiyonunun grafiğini çizip bire bir olup olmadığını
tespit ediniz.
y
y = f(x)
C
0
x
ESEN YAYINLARI
ÖRNEK 50
Çözüm
x eksenine paralel olan C doğrusu grafiği birden çok
noktada kestiğinden y = f (x) bire bir değildir.
ÖRNEK 51
f : R → R , f (x) = x + 2
fonksiyonunun grafiğini çizip bire bir olup olmadığını
ÖRNEK 54
f : R – → R , f (x) = x 2
tespit ediniz.
fonksiyonunun grafiğini çizip bire bir olup olmadığını
Çözüm
tespit ediniz.
Çözüm
274
Fonksiyon
ÖRTEN FONKSİYON
ÖRNEK 57
f : A → B fonksiyonu için f (A) = B ise yani görüntü
f : R → R , f (x) = 4x + 2 fonksiyonu örten midir?
kümesi değer kümesine eşit ise f fonksiyonu örten
Çözüm
fonksiyondur.
f
A
a
B
1
2
3
4
b
c
f : Örten de¤il
f(A) ≠ B
g
A
a
B
1
b
ÖRNEK 58
2
c
f : R → R , f (x) = x 2 – 4 fonksiyonu örten midir?
Çözüm
g : Örten
g(A) = B
ÖRNEK 55
A = {0, 1, 2 } ve B = {2, 3, 4 } olmak üzere,
f : A → B, f (x) = x + 2
Değer kümesinin her y elemanı için x eksenine
Çözüm
paralel çizilen tüm doğrular fonksiyonun grafiğini
ESEN YAYINLARI
fonksiyonunun bire bir ve örtenliğini araştırınız.
en az bir noktada kesiyorsa bu fonksiyon örtendir.
ÖRNEK 59
y
x
0
f(x) = 1 – x
ÖRNEK 56
f : Z → Z , f (x) = 2 x – 1 fonksiyonu örten midir?
x eksenine paralel çizilen doğrular grafiği en az bir
noktada kestiğinden y = f (x) , R → R ye örtendir.
Çözüm
ÖRNEK 60
y
f(x) = x2
0
x
C
x eksenine paralel çizilen doğrulardan biri olan C
doğrusu grafiği kesmediğinden y = f (x), R → R ye
örten değildir.
275
Fonksiyon
PARÇALI FONKSİYON
ÖRNEK 63
Tanım kümesinin alt aralıklarında farklı birer fonksi-
f (x) = *
yon olarak tanımlanan fonksiyona parçalı fonksiyon
x+2 , x > 1
denir.
f (x) = *
g (x) = *
3x – 1 , x < 1
x2 + 2 , x ≥ 1
2x
–x
, x≤1
, x≥2
x–2 , x<2
fonksiyonları için (f + g) (x) fonksiyonunu bulunuz.
fonksiyonu bir parçalı fonksiyondur.
Çözüm
Tanım aralığının (–∞, 1) ve [1, ∞) alt aralıklarında
fonksiyonun kuralı sırasıyla
f (x) = 3 x – 1 ve f (x) = x 2 + 2 dir.
x = 1 fonksiyonun kritik noktasıdır.
ÖRNEK 61
f (x) =
*
x3 – 1 , x < 2
2x + 3 , x ≥ 2
fonksiyonuna göre, f (3) ve f (–1) değerlerini bulunuz.
ESEN YAYINLARI
Çözüm
ÖRNEK 64
Z x+1
]
, x>2
] x –1
f (x) = [
] x+2
, x≤2
] 3
\
olduğuna göre, f ( x + 1) fonksiyonunu bulunuz.
ÖRNEK 62
f (x) = *
3x – 2 , x > 0
x+1
, x≤0
olmak üzere f (a) = 2 eşitliğini sağlayan a değerini
bulunuz.
Çözüm
276
Çözüm
Fonksiyon
ÖRNEK 65
f (x) = *
ÖRNEK 66
x+1 , x < 1
f (x) =
3 – x , x≥1
*
x2 , x < 0
–x , x ≥ 0
parçalı fonksiyonunun grafiğini çiziniz.
fonksiyonunun grafiğini çiziniz.
Çözüm
ESEN YAYINLARI
Çözüm
277
Fonksiyon
ÖRNEK 67
ÖRNEK 68
Z x
,
x<0
]
]
, 0≤ x < 2
f (x) = [ 1
]
]3– x ,
x≥2
\
fonksiyonunun grafiğini çiziniz.
f (x) = *
x+2
, x<1
olmak üzere, f (x) fonksiyonunun grafiğini çiziniz.
Çözüm
ESEN YAYINLARI
Çözüm
278
2x + 1 , x ≥ 1
Fonksiyon
MUTLAK DEĞER FONKSİYONU
ÖRNEK 71
Z
] f ( x) , f ( x) > 0
]
, f ( x) = 0
|f (x)| = [ 0
]
] –f (x) , f (x) < 0
\
biçiminde tanımlanan
y = |f (x)|
f (x) = |x – 2| + |x|
fonksiyonunu parçalı biçimde ifade ediniz.
Çözüm
fonksiyonuna
mutlak değer fonksiyonu denir. f (x) = 0 eşitliğini
sağlayan x değerleri fonksiyonun kritik noktalarıdır.
ÖRNEK 69
f (x) = |x – 2|
fonksiyonunu parçalı biçimde yazınız.
Çözüm
Mutlak Değer Fonksiyonunun Grafiği
Mutlak değer fonksiyonunun grafiğini çizerken fonk-
ESEN YAYINLARI
siyon önce parçalı biçimde yazılır, sonra da grafiği
çizilir.
ÖRNEK 72
f (x) = |x – 1|
fonksiyonunu parçalı biçimde yazıp grafiğini çiziniz.
Çözüm
ÖRNEK 70
f (x) = 2|x – 1| + 1
fonksiyonunu parçalı biçimde yazınız.
Çözüm
279
Fonksiyon
KOLAYLIK
ÖRNEK 74
Aşağıda bazı fonksiyonlarla bu fonksiyonların mutlak
y = |f ( x )| fonksiyonunun grafiği çizilirken önce
değerlerinin grafikleri çizilmiştir. İnceleyiniz.
y = f ( x ) in grafiği çizilir. Bu grafiğin y ekseninin
a.
negatif bölgesine taşan kısmının x eksenine göre
y=x
simetriği alınır.
y = | f(x) |
y = f(x)
0
–1
y= x
y
y
–3
y
y
2
x
–3
–1
0
2
x
0
x
0
x
y
y
b.
y = –x
x
0
ÖRNEK 73
Aşağıdaki fonksiyonların grafiklerini çiziniz.
x
0
y = –x
b. f : R → R , f (x) = |x – 2| + 1
Çözüm
ESEN YAYINLARI
a. f : R → R , f (x) = |x – 2|
c.
y
y
y = x2
y = x2
x
0
d.
y
x
0
y
y = x3
0
e.
y = x3
x
y
y
y= 1
x
0
280
x
0
y= 1
x
x
0
x
Fonksiyon
y = |f (x)| + g (x) Fonksiyonunun Grafiği
ÖRNEK 77
f : R → R , f (x) = x|x| + 3
y = |f (x)| + g (x) fonksiyonunun grafiği çizilirken
f (x) = 0 için kritik noktalar bulunup fonksiyon par-
fonksiyonunu parçalı biçimde yazıp grafiğini çiziniz.
çalı biçimde yazılır ve bu parçalı fonksiyonun grafiği
Çözüm
çizilir.
ÖRNEK 75
f : R – {0 } → R , f (x) =
x
x
fonksiyonunu parçalı biçimde yazıp grafiğini çiziniz.
ESEN YAYINLARI
Çözüm
ÖRNEK 78
f : R → R , f (x) = |x – 2| + 2 x
fonksiyonunun grafiğini çiziniz.
Çözüm
ÖRNEK 76
f : R → R , f (x) = |x| – x
fonksiyonunu parçalı biçimde yazıp grafiğini çiziniz.
Çözüm
281
Fonksiyon
ÖRNEK 79
KOLAYLIK
f : R → R , f (x) = |x – 1| + x – 2
f(x) = |x – a| + |x – b|
fonksiyonunu parçalı biçimde yazıp grafiğini çiziniz.
fonksiyonunun en küçük değeri :
Çözüm
f(a) = f(b) = |a – b| olup
(a, f(a)) ve (b, f(b)) kırılma noktalarıdır.
y
|a – b|
0
a
b
ÖRNEK 81
f : R → R , f (x) = |x – 2| + |x + 1|
fonksiyonunun grafiğini çiziniz.
ÖRNEK 80
f : R → R , f (x) = |x – 1| + |x + 1|
ESEN YAYINLARI
Çözüm
fonksiyonunu parçalı fonksiyon biçiminde yazıp grafiğini çiziniz.
Çözüm
ÖRNEK 82
f : R → R , f (x) = |x | + |x – 1|
fonksiyonunun grafiğini çiziniz.
Çözüm
282
x
Fonksiyon
ÖRNEK 83
ÖRNEK 84
f : R → R , f (x) = |x + 2| – |x|
f : R → R , f (x) = |x + 2| – |x – 1|
fonksiyonunun grafiğini çiziniz.
Çözüm
Çözüm
ESEN YAYINLARI
fonksiyonunun grafiğini çiziniz.
ÖRNEK 85
f : R → R , f (x) = |x | – |x – 1|
fonksiyonunun grafiğini çiziniz.
Çözüm
KOLAYLIK
f ( x ) = |x – a| – |x – b| fonksiyonunun;
en küçük değeri f(a ) = – |a – b|
en büyük değeri f(b ) = |b – a| dır.
( a, f ( a )) ve ( b, f ( b )) kırılma noktalarıdır.
y
|b – a|
a
0
b
x
– |a – b|
283
ALIŞTIRMALAR -
2.
3.
Aşağıdaki fonksiyonlardan hangileri bire bir
Aşağıdaki fonksiyonlardan hangileri örten fonk-
fonksiyondur?
siyondur?
a. f : R → R , f (x) = 2 x + 5
a. f : R → R , f (x) = 2 x – 3
b. g : R → R , g (x) = x 2 – 2
b. g : R → R , g (x) = x 2 + 2
c. h : R+ → R , h (x) = x 2 + 1
c. h : Z → Z , h (x) = 3 x – 2
d. k : R+ → R , k (x) = x 2 – 4x
d. k : R → R , k (x) = x 3
4.
Aşağıdaki fonksiyonlardan hangileri bire bir
a.
Aşağıdaki fonksiyonlardan hangileri R → R ye
örtendir?
fonksiyondur.
a.
y
y
f
f
0
b.
x
y
g
c.
b.
y
g
c.
y
x
0
x
0
x
0
ESEN YAYINLARI
1.
3
y
h
h
x
0
d.
x
0
y
d.
k
0
y
x
x
0
k
284
Fonksiyon
5.
Z 2
]x ,
]
f (x) = [ 0 ,
]
] –x ,
\
olduğuna göre,
x >1
9.
x =1
x <1
f (x) = *
x
, x≥0
3x , x < 0
fonksiyonunun grafiğini çiziniz.
f (–1) + f (1) + f (2) ifadesinin
eşitini bulunuz.
10.
6.
f : A → [ –6, 3] , f (x) = 2 – x 3
f (x) = *
x+1 , x < 3
2–x , x≥3
fonksiyonunun grafiğini çiziniz.
fonksiyonu bire bir ve örten ise tanım kümesini
ESEN YAYINLARI
bulunuz.
7.
f : R → R , f (x) = 2 – |x| fonksiyonunun görüntü
11.
kümesini bulunuz.
8.
f (x) = *
, x≥1
olmak üzere, f(m) = 5 eşitliğini sağlayan m
değerini bulunuz.
1– x , x ≤ 2
x2
, x>2
fonksiyonunun grafiğini çiziniz.
2x – 1 , x < 1
x+3
f (x) = *
12.
Z 2
,
x≤0
] x
]
f (x) = [ 0
, 0<x≤2
]
]x–2 ,
x>2
\
fonksiyonunun grafiğini çiziniz.
285
Fonksiyon
Zx+2 ,
x≤0
]
] 2
, 0<x<2
f (x) = [ x
]
] 4
,
x≥2
\
13.
17. Aşağıdaki tablonun sol sütununda bulunan
fonksiyonların grafiklerini sağ sütunda bulup
eşleştiriniz.
fonksiyonunun grafiğini çiziniz.
1
a
y
3
y = |3 – x|
0
2
b
14.
x
3
y
f : R → R , f (x) = |x| – |x – 2|
2
fonksiyonunun grafiğini çiziniz.
2
y = 2 – |x|
x
0
ESEN YAYINLARI
–2
15.
3
c
y
1
y = |x – 2| – x
f : R → R , f (x) = x .|x|
0
fonksiyonunun grafiğini çiziniz.
4
d
x
1
y
4
0
y = |x – 1| + |x|
2
x
–2
–4
16.
f : R → R , f (x) = |x + 3| + |x|
5
e
y
fonksiyonunun grafiğini çiziniz.
2
y=|x–2| – |x+2|
–2
2
0
286
x
Yazılıya Hazırlık Soruları
1.
4.
Aşağıda sol sütunda verilen 1 – 1 ve örten
A = {a, b, c } ve B = {1, 2, 3, 4, 5 }
fonksiyonların görüntü kümelerini sağ sütundan
olmak üzere, A → B ye tanımlanan aşağıdaki
bulup eşleştiriniz.
bağıntıların fonksiyon olup olmadığını araştırınız.
1
f : [–3, 4] → A, f(x) = 2x – 1
b
f : [–1, 7] → B, f(x) =
c
f : [–3, 7] → C, f(x) =
2.
3x + 1
2
1–x
2
a. f1 = {(a, 1), ( b, 2), (c, 2) }
[–1, 11]
b. f2 = {(a, 1), (a, 2), ( b, 3), (c, 5) }
2
[–3, 2]
c. f3 = {(a, 1), ( b, 1), (c, 2) }
3
[–7, 7]
f (x + 1) + f (x – 2) = 4x – 1
d. f4 = {(a, 1), ( b, 3) }
ESEN YAYINLARI
a
5.
fonksiyonuna göre, f (5) – f (–1) ifadesinin eşiti
olduğuna göre f (x + 1) fonksiyonunun f e
kaçtır?
3.
f (x – 1) = 2 x + 2
cinsinden değerini bulunuz.
f : [0, 4 ] → R , f (x) = x 2 – 6 x + 1
fonksiyonunun görüntü kümesini bulunuz.
x
o
2
6.
f (x) =
*
x + 3 , x 1 –1
1– x , x $ – 1
fonksiyonunun grafiğini çiziniz.
287
Fonksiyon
7.
y
y
9.
y = f (2x – 1)
3
y = f(x)
2
–4
0
–3
0
1
1
3
x
x
Şekildeki grafik y = f (x) fonksiyonuna aittir.
x .f (x) ≤ 0
Şekildeki grafik y = f (2 x – 1) fonksiyonuna
aittir. Buna göre
f (–7) + f (1)
f (–1)
eşitsizliğinin çözüm kümesini bulunuz.
ifadesinin eşiti
ESEN YAYINLARI
kaçtır?
8.
f (x) =
x
x
+x–2
fonksiyonunu parçalı fonksiyon biçiminde yazıp
grafiğini çiziniz.
288
10.
f (x) = |x + 2| – |x – 1|
fonksiyonunu parçalı fonksiyon biçiminde yazıp
grafiğini çiziniz.
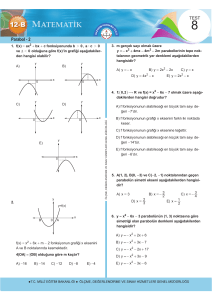
TEST -
1.
1
Fonksiyonlar
5.
Aşağıdaki bağıntılardan hangisi A dan B ye bir
fonksiyon değildir?
A
B
1
3
1
2
3
4
A
B
2
C)
E)
2.
olduğuna göre, aşağıdakilerden hangisi f (x)
B)
A
1
D)
B
fonksiyonunun görüntü kümesinin elemanı
1
değildir?
2
A) –1
2
3
A
B
1
1
1
1
2
2
2
2
3
3
3
3
4
4
4
6.
B) 0
C) 3
D) 5
E) 8
f : A → B , f (x) = x + 3 , f (A) = {3, 5, 8, 9}
A
B
olduğuna göre, aşağıdakilerden hangisi A tanım
1
1
kümesinin elemanı değildir?
2
2
3
3
4
4
A) –1
f : R → R , f (x) = (a – b)x + 2a + b – 2
B) 0
C) 2
D) 5
E) 6
ESEN YAYINLARI
A)
f : A → B , f (x) = x 2 – 1 ve A = {0, 1, 2, 3 }
fonksiyonu birim fonksiyon ise a.b kaçtır?
A) 0
B) 1
C) 2
D) 3
E) 4
7.
f : A → B , f (x) =
2–x
3
ve A = (3, 5 ]
olduğuna göre f (A) görüntü kümesi aşağıdakilerden hangisidir?
3.
a.f (x) – 3 = x .f (x) + b. x
A) [ –1, –
1
)
3
B) [ –1, 1)
C) (
1
, 1]
3
eşitliğini sağlayan f (x) sabit fonksiyon ise a.b
D) (–13, –7 ]
kaçtır?
A) –3
4.
B) –2
C) –1
D) 0
E) [ –13, –7 )
E) 1
f (x) doğrusal bir fonksiyondur.
8.
f (1) = 3 ve f (0) = 2
olduğuna göre f (8) kaçtır?
olduğuna göre, f (3) kaçtır?
A) 1
B) 2
C) 3
f (x + 2) = x – f (x) ve f (2) = 4
D) 4
E) 5
A) 0
B) 2
C) 4
D) 6
E) 8
289
Fonksiyon
Z 2x , x > 3
]
]
f (x) = [ 0 , x = 3
]
] –x , x < 3
\
9.
13.
y
2
fonksiyonu için f (2) + f (3) + f (4) toplamının
sonucu nedir?
A) 4
B) 6
f
4
1
–4
–2
C) 8
D) 10
1
0
x
2
E) 12
–2
Şekildeki grafik y = f (x) fonksiyonuna aittir.
f (– 4) + f (–2) + f (0) – f (1) – f (2)
ifadesinin eşiti nedir?
10.
A) –8
f : R → R , f (x + 3) = 2 x + 5
B) –7
C) –6
D) –5
E) –4
olduğuna göre f (4) = 2k – 3 eşitliğini sağlayan
k kaçtır?
B) 5
C) 6
D) 8
E) 9
ESEN YAYINLARI
A) 4
11
Z
, x≥1
] –1
14.
f (x) = [
] 1 – 2x , x < 1
\
fonksiyonunun grafiği aşağıdakilerden hangisidir?
f (x) = (m – 1) x + 2m – 6
fonksiyonunun grafiği x eksenini 2 apsisli nok-
A)
B)
y
y
tasında kesiyorsa y eksenini kestiği noktanın
1
1
ordinatı kaçtır?
A) –2
B) –1
C) 1
D) 2
0
–1
E) 3
C)
0
–1
x
D)
y
y
1
1
0
12.
1
x
f (x) = 3 x – 2
olduğuna göre f (2 x – 1) fonksiyonunun f (x)
türünden yazılışı hangisidir?
A) 2f (x)
B) 2f (x) – 1
D) 3f (x) – 1
290
E)
y
1
C) 2f (x) + 1
E) 3f (x) + 1
0
x
1
x
1
0
–1
x
TEST -
1.
2
Fonksiyonlar
4.
Aşağıdaki grafiklerden hangisi bir fonksiyon
grafiği değildir?
A)
f (1) = 5 ve f (–1) = 3 ise f (2) kaçtır?
B)
y
A) 6
y
1
B) 5
C) 4
D) 3
E) 2
2
0
2
C)
f (x) doğrusal fonksiyon olmak üzere,
x
0
D)
y
x
2
y
1
0
x
x
0
5.
f (2 x + 1) = 2 – m x
ve f (3) = 5
olduğuna göre m kaçtır?
E)
A) –3
y
0
C) –1
D) 0
E) 2
x
ESEN YAYINLARI
–2
B) –2
2.
Aşağıdaki fonksiyonlardan kaç tanesi bire birdir?
6.
fonksiyonu için
I. f : R → R , f (x) = 2 – 3 x
III. f : R → R , f (x) =
f (4) – f (5) – f (6)
işleminin
sonucu nedir?
II. f : R → R , f (x) = x 2 + 2
3
f (2x) + f (x + 2) = 4x
A) –2
B) –4
C) –6
D) –8
E) –10
x –1
IV. f : R+ → R , f (x) = x 2 – 4
V. f : R → R , f (x) = x 3 + 1
A) 1
3.
B) 2
C) 3
D) 4
E) 5
f (x) = (a – 2)x + b + 1
7.
g (x) = (c + 3)x + a.b
f : [ –2, 4] → R , f (x) = x 2 – 3
olmak üzere, f (x) birim fonksiyon ve g (x) sabit
fonksiyonunun görüntü kümesinde kaç farklı
fonksiyon ise a + b + c kaçtır?
tam sayı vardır?
A) –3
B) –2
C) –1
D) 0
E) 1
A) 15
B) 16
C) 17
D) 18
E) 19
291
Fonksiyon
8.
2x – 1
3
f : A → B , f (x) =
olduğuna göre
A
12.
ve f (A) = [ 3, 7 ]
y
f(x + 2)
6
kümesi aşağıdakilerden
hangisidir?
2
A) (5, 11)
B) [ 5, 11]
D) [ 6, 10 ]
C) (6, 10)
–3
E) [ 6, 12 ]
x
4
0
Şekilde f (x + 2) fonksiyonunun grafiği verilmiştir. Buna göre, f (2) + f (–1) + f (6) ifadesinin
değeri kaçtır?
A) 10
9.
f (2x) = 2.f (x) + x
B) 9
C) 8
D) 7
E) 6
ve f (–2) = 2
olduğuna göre f (–16) kaçtır?
B) –8
C) –4
D) –2
E) 0
ESEN YAYINLARI
A) –16
10.
f (x + 1) – 3 =
x
.f (x) ve f (3) = 12
4
13.
f (x) = x + |x|
fonksiyonunun grafiği aşağıdakilerden hangisidir?
A)
olduğuna göre, f (4) kaçtır?
A) 16
B) 15
C) 14
x
0
D) 13
B)
y
D)
y
x
0
f (x) = 21 – 2 x
olduğuna göre f (x + 1) in f (x) cinsinden değeri
E)
y
nedir?
A)
f (x)
2
B)
D) 4f (x)
292
f (x)
4
C) 2f (x)
E) 2f2 (x)
x
0
E) 12
C)
11.
y
0
x
y
0
x
TEST -
1.
fc
5
Fonksiyonlar
ax + 3
m = x – 2 ve f (5) = 0
2
4.
olduğuna göre a kaçtır?
A) 5
B)
9
2
C) 4
D)
7
2
E) 3
Z
x < –2
] –2x – 1 ,
]
3
, –2 ≤ x < 1
f (x) = [
]
] 2x + 1 ,
x≥1
\
fonksiyonunun grafiği aşağıdakilerden hangisidir?
A)
B)
y
y
3
3
0 1
–2
y
2.
–2
x
0 1
–3
–3
1
–1
C)
D)
y
y
3
x
0
x
1
–2
Şekildeki grafik aşağıdaki fonksiyonlardan hangisine ait olabilir?
E)
ESEN YAYINLARI
A) f (x) = |x + 1| + 1
B) f (x) = |x + 1| + x
C) f (x) = |x + 1| + |x|
D) f (x) = |x + 1| – x
0
1
x
–2
0
x
1
y
3
–2
0
1
x
E) f (x) = |x + 1| – |x|
5.
x+ x
2
f (x) =
fonksiyonunun grafiği aşağıdakilerden hangisidir?
3.
A)
y
1
0
B)
y
0
x
0
y
x
x
C)
D)
y
y
Şekildeki grafik aşağıdaki fonksiyonlardan hangisine ait olabilir?
A) |y| = x + 1
C) y =
x
x2
+1
E) y = |x| + 2 – x
x
0
x
0
B) y = |x| + 1
x2
D) y =
+1
x
E)
y
0
x
297
Fonksiyon
6.
f (x) = |x| + x + 2
8.
fonksiyonunun grafiği aşağıdakilerden hangisidir?
f (x) = *
2x + 2 , x ≥ 2
4x – 2 , x < 2
fonksiyonunun eşiti aşağıdakilerden hangisidir?
A)
B)
y
y
2
2
C)
D)
y
x
0
x
0
A) 2 x – |x – 2|
B) 3 x + |x – 2|
C) |x – 2| + 2 x
D) 3 x – |x – 2|
E) |x – 2| – 2 x
y
y
9.
2
2
x
0
E)
x
0
2
y
0
x
1
Şekildeki grafik aşağıdaki fonksiyonlardan han-
2
x
0
gisine ait olabilir?
7.
x
f (x) =
x
ESEN YAYINLARI
A) y = |x – 1| + 1
+1
B) y = |x – 1|
C) y = |x – 1| + |1 – x|
D) y = |2 x – 1|
E) y = |x| + 2
fonksiyonunun grafiği aşağıdakilerden hangisidir?
A)
B)
y
2
y
2
10.
1
x
0
y
1
x
0
–1
0
C)
D)
y
2
–1
y
1
x
0
x
0
–1
–2
E)
y
0
Şekildeki grafik aşağıdaki fonksiyonlardan hangisine ait olabilir?
A) f (x) = |x| – x + 1
B) f (x) = |x + 1| – |x| + 1
1
C) f (x) = |x + 1| – |x|
x
–1
D) f (x) = |x| – |x + 1| + 2
E) f (x) = |x + 1| – x
298
x
Üniversiteye Giriş Sınav Soruları
1.
1977 – ÜSS
4.
y
1985 – ÖYS
f (ab) = f (a) + f ( b)
olduğuna göre, f (1) in değeri nedir?
1
A) 0
0
1
B) 1
C) a
D) b
E) ab
D) 4
E) 5
x
2
Şekilde verilen grafiğin denklemi aşağıdakilerden hangisidir?
A) y = |x + 1|
B) y = |x| – 1
D) y = |x – 1|
C) y = 1 – |x|
E) y = |x| + 1
5.
1987 – ÖYS
f (x) doğrusal fonksiyonu için
2.
1978 – ÜSS
f (2) = 3 ve f (3) = 2
y
olduğuna göre, f (1) kaçtır?
a
x
0
–a
Grafiği verilen fonksiyon aşağıdakilerden hangi-
B) 2
C) 3
ESEN YAYINLARI
A) 1
a
sidir?
A) y =
x–a
a
B) y = |x| + |x – a|
6
f (2 x + 3) = 3 x + 2
C) y = |x – a| – |x|
D) y = |x| – |x – a|
olduğuna göre, f (0) kaçtır?
E) y = x|x – a|
3.
1987 – ÖYS
1982 – ÖYS
A) –
5
2
B) –
3
2
C) –
1
2
D) 0
E)
y
5
3
0
4
x
7
7.
1988 – ÖSS
f (x) = x 3 – 3 x 2 + 3 x – 1
Bir y = f (x) fonksiyonunun grafiği yukarıda
verilmiştir.
f[ f (x)] = 3
olduğuna göre, x in
değeri nedir?
A) 7
B) 6
C) 5
D) 4
E) 3
olduğuna göre, f (x + 1) değeri nedir?
A) x 3 + 1
B) x 3 – 1
D) x 2
C) x 3
E) x 2 + 1
299
2
3
Fonksiyon
8.
1989 – ÖYS
11. 1992 – ÖSS
y
f(x) = |2 – x| – x
fonksiyonunun grafiği aşağıdakilerden hangisi
olabilir?
1
A)
B)
y
–1
y
x
0
2
–2
2
x
0
–2
C)
Yukarıda grafiği verilen f (x) doğrusal fonksiyo-
–2
D)
y
nu aşağıdakilerden hangisidir?
A) y = x
y
1 2
x
0
0
–2
B) y = – x
D) y = – x + 1
2
2
E)
x
0
C) y = – x – 1
E) y = x + 1
x
1 2
–2
y
2
x
2
ESEN YAYINLARI
0
12. 1996 – ÖYS
f (x) = 3.f (x – 2) , f (5) = 6
olduğuna göre, f (1) değeri kaçtır?
A)
9.
1
4
B)
2
3
C)
1
2
D) 1
E) 2
1990 – ÖYS
f (x) = 23 x – 1
olduğuna göre, f (2x) in f (x) cinsinden ifadesi
aşağıdakilerden hangisidir?
B) 3[ f (x)] 2
A) 3f (x)
D) 2[ f (x)] 2
C) 2f (x)
E) 2[ f (x)] 3
13. 1997 – ÖSS
10. 1991 – ÖYS
f (x) : R → R
f (x) : R → R
f (x) = x .f (x + 1) , f (4) =
f (x) = 2 x + 1 – f (x + 1)
4
3
f (4) = 2
olduğuna göre, f (2) değeri kaçtır?
A) 14
300
B) 12
C) 10
D) 8
olduğuna göre, f (2) nin değeri kaçtır?
E) 6
A) 0
B) 1
C) 2
D) 3
E) 4
Fonksiyon
14. 1998 – ÖSS
Bir
f
17. 2008 – ÖSS
fonksiyonu, “Her bir pozitif tam sayıyı
Aşağıda A = {a1, a2, a3 } ve
kendisi ile çarpımsal tersinin toplamına götü-
B = {b1, b2, b3, b4, b5 } kümeleri verilmiştir.
rüyor” şeklinde tanımlanmıştır. Bu fonksiyon
aşağıdakilerden hangisi ile gösterilebilir?
A) f (x) =
x2 + x
B) f (x) =
x –1
C) f (x) =
x
x2 + 1
E) f (x) =
x2 + 1
x
D) f (x) =
x2
f
A
x
–1
B
b1
a1
b2
x2 – 1
x
a2
b3
a3
b4
b5
A dan B ye f (a2 ) = b4 olacak biçimde kaç tane
birebir f fonksiyonu tanımlanabilir?
A) 24
B) 20
C) 16
D) 12
E) 10
18. 2009 – ÖSS
f (x) = x 2 – x – 1
olduğuna göre, f (1 – x) – f (x) aşağıdakilerden
hangisine eşittir?
A) 0
B) 1
2
D) x – 1
C) 1 – x
ESEN YAYINLARI
15. 1999 – ÖSS
y
f(x)
3
2
1
5
4
2
O
2
E) x + 1
5
1
x
2
3
Yukarıda grafiği verilen f (x) fonksiyonu için
[–5, 5 ] aralığında
| |f(x) | – 2 | = 1
eşitliğini
sağlayan kaç tane x değeri vardır?
A) 3
16. 2007 – ÖSS
B) 4
C) 5
D) 6
E) 7
R den R ye f (x) = 3 x+2 ile tanımlı f fonksiyonu
için,
f (a + b – 1)
ifadesi aşağıdakilerden
hangisine eşittir?
f (a + b)
9
B)
C)
f (a) .f (b)
9
D)
E)
f (a) .f (b)
81
A)
f (a + b)
27
f (a) .f (b)
27
19. 2010 – YGS
f (x) = x 2
g (x) = 2 x – 1
fonksiyonları için g (f (2)) kaçtır?
A) 0
B) 3
C) 5
D) 7
E) 9
301
Fonksiyon
20. 2010 – LYS
23. 2011 – YGS
Gerçel sayılar kümesinde tanımlı
Gerçel sayılardan gerçel sayıların bir K alt
kümesine tanımlı
f (x) =
*
I. f (x) = 2 x – 1
–x+8 ,
x<3
x+2 ,
x≥3
II. g (x) = x 2 + 2
III. h (x) = x 3
fonksiyonu örten olduğuna göre, K kümesi
fonksiyonlarından hangileri bire birdir?
aşağıdakilerden hangisidir?
A) I ve II
A) [ 3, ∞ )
B) [ 5, ∞ )
D) (– ∞, 5)
C) [ 3, 5 ]
B) Yalnız I
D) I ve III
C) I, II ve III
E) Yalnız II
E) (– ∞, 3)
21. 2010 – LYS
24. 2011 – LYS
x –1
m = x2 – x + 2
x +1
Aşağıda f fonksiyonunun grafiği verilmiştir.
olduğuna göre, f (3) değeri kaçtır?
A) 5
B) 6
C) 7
D) 8
E) 11
ESEN YAYINLARI
fc
y
f(x)
4
3
1
–4
–2
0
–1
2 3
x
g (x) = 3 – f (x – 2) olduğuna göre, g (–2) + g (5)
toplamı kaçtır?
22. 2010 – LYS
A) – 3
y
B) – 1
C) 1
D) 2
E) 3
4
2
–3
O
3
7
x
–2
Yukarıda grafiği verilen f fonksiyonunun tanım
25. 2011 – LYS
kümesi aşağıdakilerden hangisidir?
f fonksiyonu n ≥ 1 tam sayıları için,
A) [ –3, 0) ∪ [4, 7 )
B) (–3, 0) ∪ (3, 7 ]
f (n) = 2.f (n – 1) + 1 eşitliğini sağlıyor.
C) [ –3, 2 ] ∪ (3, 7 )
D) (–3, 3) ∪ (3, 7 ]
f (0) = 1 olduğuna göre, f (2) kaçtır?
E) [ –3, 2) ∪ (4, 7 ]
302
A) 8
B) 7
C) 6
D) 5
E) 4
Fonksiyon
26. 2012 – LYS
28. 2012 – YGS
Z tam sayılar kümesi olmak üzere,
R gerçel sayılar kümesi üzerinde tanımlı bir f
f : Z → Z fonksiyonu,
fonksiyonu
f(x) = *
x – 1 , x 1 0 ise
•
Her x ∈ [ –10, 10 ] için f (x) = |x|
x + 1 , x $ 0 ise
•
Her x ∈ R için f (x) = f (x + 20)
biçiminde tanımlanıyor.
özelliklerini sağladığına göre, f (117 ) değeri
Buna göre,
kaçtır?
I. f bire birdir.
A) 3
B) 4
C) 6
D) 7
E) 9
II. f örtendir.
III. f nin görüntü kümesi Z \ { 0 } dır.
ifadelerinden hangileri doğrudur?
A) Yalnız I
B) Yalnız II
D) I ve II
C) Yalnız III
E) I ve III
29. 2013 – YGS
ESEN YAYINLARI
A = { 1, 2, 3, 4, 5, 6 } olmak üzere, f : A → A
fonksiyonu bire birdir.
Buna göre,
f(1) + f(2) + f(3) + f(4)
toplamının alabileceği en büyük değer ile en
küçük değer arasındaki fark kaçtır?
A) 6
B) 7
C) 8
D) 9
E) 10
27. 2012 – LYS
Gerçel sayılar kümesi üzerinde tanımlı bir f
fonksiyonu, her x gerçel sayısı için
f(x) < f(x + 2)
eşitsizliğini sağlıyor.
30. 2013 – YGS
Buna göre,
I.
f(x) = 2x
I. f(1) < f(5)
II.
f(x) = 2x
II. | f(–1) | < | f(1) |
III. f(x) = x2
III. f(0) + f(2) < 2.f(4)
fonksiyonlarından hangileri, her a ve b gerçel
ifadelerinden hangileri her zaman doğrudur?
sayısı için f(a + b) = f(a).f(b) eşitliğini sağlar?
A) Yalnız I
A) Yalnız I
B) Yalnız II
D) II ve III
C) I ve III
E) I, II ve III
B) Yalnız II
D) I ve III
C) I ve II
E) II ve III
303
ESEN YAYINLARI
Fonksiyon
304