Elektromanyetik Dalga Teorisi Ara Sınavı (2.Ö) 16.11.2016 1

Elektromanyetik Dalga Teorisi Ara Sınavı (2.Ö)
16.11.2016
Numara:…………………………………………..
1
2
3
4
T
Ad-Soyad:…………………………………………
SORULAR
1) Aşağıda verilen ifadelerin doğru veya yanlış olduğunu belirleyiniz. (20P)
( D / Y ) Elektrik alan bileşeni 𝐸⃗ = 50. 𝑒 −𝑗1.2𝑧 . 𝚤̂𝑦 [V/m] olan dalga -z yönünde yayılmaktadır.
( D / Y ) Uzak infrared dalgaları, ısısal özelliğe sahiptir.
( D / Y ) +z doğrultusunda yayılan elektromanyetik dalganın z=0’daki elektrik alan ifadesi
𝐸⃗ (0, 𝑡) = (𝐸0 . 𝚤̂𝑥 + 𝑗. 𝐸0 . 𝚤̂𝑦 ). cos⁡(𝑤𝑡) olduğuna göre, bu dalga sol-el dairesel polarizasyonludur.
( D / Y ) Kırılma açısının π/2 olduğu tam yansımanın eşiğine karşılık gelen geliş açısına Brewster açısı denir.
( D / Y ) Duran dalga oranı 1.5 olan iletim hattının yansıma katsayısı genliği 0.2’dir.
(D/Y)


J   .E denklemi ohm kanununu ifade eder.
c
( D / Y ) Kayıpsız bir iletim hattının sonunun kısa devre yapılması durumunda dalga hat sonundan 180 derece faz
farkıyla yansır.
( D / Y ) 100 ohm’luk bir iletim hattına 36 ohm’luk yük bağlanması durumunda, girişten 36 ohm görünmesi için
araya uzunluğu ℓ=λ/2 olan 80 ohm’luk iletim hattı bağlamak gerekir.
( D / Y ) İki iletkenli ve koaksiyel hatlar birer alçak geçiren filtre gibi davranırlar.
( D / Y ) Dielektrik katsayısı birimi (H/m)’dir.
⃗⃗ = 𝟖. 𝒆−𝒋𝟏.𝟓𝒙 . 𝚤̂𝒛 ⁡[ 𝑽 ]⁡veriliyor. Dalganın
2) Manyetik olmayan bir ortamda (𝜺𝒓 ≠ 𝟏, 𝝈 = 𝟎) 𝑬
𝒎
frekansı 30 MHz olduğuna göre,
a) Ortam empedansını (5P)
b) Manyetik alanın anlık ifadesini (10P)
c) Dalganın taşıdığı ortalama gücü bulunuz (10P)
Çözüm:
=1.5
a)
𝛽=
𝜔.√𝜀𝑟
𝑐
𝜇0
𝜂=√
𝜀
𝑟 𝜀0
f = 30.⁡106
√𝜀𝑟 =
⁡=⁡
120𝜋
√ 𝜀𝑟
𝛽.𝑐
𝜔
=
𝜔 = 2𝜋𝑓 = 2𝜋30. 106 = 1,885. 108
1,5⁡.3.108
1,885⁡108
= 2.38
𝜀𝑟 = 5.66
⁡= 158.4
⃗ = − 8 𝑐𝑜𝑠(1.885108 𝑡 − 1.5𝑥) 𝚤̂𝑦
b) 𝐻
158.4
⃗ 𝑜𝑟𝑡 =
c) 𝑃
𝐸0 2
2.𝜂
. 𝚤̂𝑥 = ⁡
16
2.158.4
𝚤̂𝑥 = 0.05. 𝚤̂𝑥 ⁡[
𝑊
𝑚2
]
3) Serbest uzayda (z  0) düzlem dalganın manyetik alan bileşeni
⃗𝑯
⃗⃗ 𝒊 = 𝟏𝟎. 𝐜𝐨𝐬(𝟏𝟎𝟖 𝒕 − 𝜷𝒛) 𝚤̂𝒙 ⁡[𝒎𝑨] veriliyor. Dalga z  0’da bulunan ortama yüzey normali
𝒎
doğrultusunda geçiyor. Dalganın taşıdığı gücün %20’si geri yansıdığına göre.
a) Faz sabitini () bulunuz (5P)
⃗ 𝒊 (𝒛, 𝒕), ⃗𝑬
⃗ 𝒓 (𝒛, 𝒕) )
b) Gelen ve yansıyan elektrik alan bileşeninin anlık ifadesini ( ⃗𝑬
yazınız. (10P)
c) İkinci ortamın dielektrik sabitini bulunuz (10P)
Çözüm:
a)  =
𝜔
𝑐
=
108
3.108
=
1
3
b) Gücün %20’si yansıdığına göre;
𝐸𝑟 2
2.𝜂
𝐸𝑖 2
2.𝜂
Γ=
= 0.2 yazılabilir.
𝐸𝑟 = 
√0.2 =⁡−0.447
𝐸𝑖
Gelen elektrik alan bileşeni;
𝑚𝑉
𝐸⃗𝑖 (𝑧, 𝑡) = −10. 𝜂0 . cos(108 𝑡 − 𝛽𝑧) 𝚤̂𝑦 ⁡[ ]
𝑚
Yansıyan elektrik alan bileşeni;
𝑚𝑉
𝐸⃗𝑟 (𝑧, 𝑡) = −10. (−0.447). 𝜂0 . cos(108 𝑡 + 𝛽𝑧) 𝚤̂𝑦 ⁡[ ]
𝑚
𝑚𝑉
𝐸⃗𝑟 (𝑧, 𝑡) = 4.47. 𝜂0 . cos(108 𝑡 + 𝛽𝑧) 𝚤̂𝑦 ⁡[ 𝑚 ]
c)
Γ=
⁡𝜂 −𝜂
𝐸𝑟 = 
√0.2 =⁡ 𝜂 2+𝜂 1
𝐸𝑖
2
1
𝜀
√𝜀0 ⁡−⁡1⁡
Γ=
2
𝜀0
√𝜀 ⁡+⁡1⁡
2
= −0.447
𝜀2 = 7.14. 𝜀0
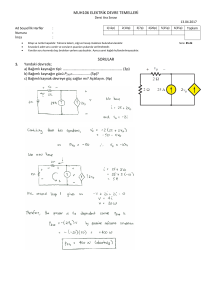
4)
Yandaki şekilde verilen kayıpsız bir iletim hattı
için;
a) Yansıma katsayısı ve duran dalga oranını
b) Kaynaktan görülen giriş empedansını
hesaplayınız.
Çözüm:
𝑍 −𝑍
Duran dalga oranı;
𝐿
𝑍 +𝑗𝑍 tan(𝛽𝑙)
𝑍𝑖𝑛 = 50
𝐿
0
1+|𝛤|
𝑠 = 1−|𝛤|=2.39
b) 𝑍𝑖𝑛 = 𝑍0 𝑍𝐿+𝑗𝑍0 tan(𝛽𝑙)
0
120−50
𝛤 = 𝑍𝐿 +𝑍0 = 120+50 = 0.41
a) Yansıma Katsayısı;
𝛽𝑙 =
2𝜋 
 6
=
𝜋
3
= 60°
120 + 𝑗50tan⁡(60)
120 + 𝑗86.6
120 + 𝑗86.6
147.98 < 35.816°
= 50
= 50
= 50
= 34.62 < −40.65° 𝛺
50 + 𝑗120tan⁡(60)
50 + 𝑗207.84
50 + 𝑗207.84
213.77 < 76.47°